	Biologie	Chimie	Didactica	Fizica	Geografie	Informatica
	Istorie	Literatura	Matematica	Psihologie

Matematica

Index » educatie » Matematica
» Rezolvarea problemelor cu ajutorul simetriei

Rezolvarea problemelor cu ajutorul simetriei

Rezolvarea problemelor cu ajutorul simetriei

Rezolvarea problemelor cu ajutorul simetriei fata de un punct

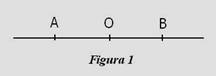Definitia 1: Fiind dat un punct fix O in plan (vezi Figura 1), doua puncte A si B se zice ca sunt simetrice fata de punctul O, daca punctul O este mijlocul segmentului [AB], adica:

OA=OB

Punctul fix O se numeste centru de simetrie. Din cele spuse mai sus rezulta ca, pentru a construi simetricul unui punct A, cand cunoastem centru de simetrie O, se uneste A cu O si pe prelungirea [AO] luam segmentul [OB], congruent cu segmentul [OA].

Teorema 2: Doua segmente de dreapta simetrice fata de un centru de simetrie sunt paralele si congruente.

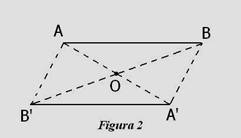Demonstratie: Intr-adevar, fie O centrul de simetrie si segmentele [AB] si [A¢B¢ simetrice fata de punctul O (vezi Figura 2). Sa aratam ca segmentele [AB] si [A¢B¢ sunt paralele si congruente. Patrulaterul ABA¢B¢ este un paralelogram, deoarece, conform ipotezei, diagonalele [AA¢ si [BB¢ se injumatatesc. Deci

AB A¢B¢

Pe de alta parte, intr-un paralelogram laturile opuse sunt congruente, deci

AB=B¢A¢ ð

Teorema 3: Doua figuri simetrice fata de un punct sunt congruente.

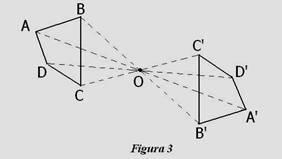Demonstratie: Intr-adevar fie O punctul dat si luam o figura, de exemplu patrulaterul ABCD, care este simetric cu patrulaterul A¢B¢C¢D¢ (vezi Figura 3). Pentru a arata ca patrulaterele ABCD si A¢B¢C¢D¢ sunt congruente, trebuie sa aratam ca ele au unghiurile si laturile respectiv congruente. Intr-adevar, laturile [AB] si [A¢B¢ fiind simetrice fata de punctul O, pe baza rezultatului gasit mai sus, ele sunt congruente si paralele. De asemenea, latura [BC] este paralela si egala cu [B¢C¢ . De aici rezulta ca unghiul ABC este congruent cu unghiul A¢B¢C¢ ca unghiuri formate de laturi paralele si indreptate in sens contrar. La fel se arata ca si celelalte laturi si unghiuri respective, sunt congruente, deci figura ABCD este congruenta cu figura A¢B¢C¢D¢ ð

Rezolvarea problemelor cu ajutorul simetriei fata de o dreapta

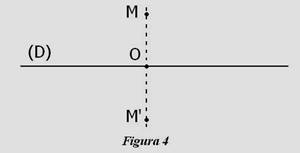
Definitia Fiind date in plan o dreapta fixa (D) (vezi Figura 4), doua puncte M si M¢ se spune ca sunt simetrice fata de dreapta (D) atunci cand dreapta (D) este perpendiculara pe segmentul [MM¢ in mijlocul acestuia.

Dreapta fixa (D) se numeste axa de simetrie.

Din definitia de mai sus rezulta ca, pentru a gasi simetricul unui punct M fata de o dreapta (D), se duce din punctul M o perpendiculara pe aceasta dreapta, apoi, pe prelungirea acestei perpendiculare luam segmentul [OM¢ congruent cu segmentul [OM].

Punctele de pe axa de simetrie sunt propriile lor simetrice. Alte puncte nu mai au aceasta proprietate.

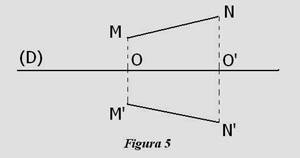
Simetricul unui segment de dreapta [MN] fata de o dreapta (D) se obtine unind printr-o dreapta simetricele punctelor M si N (vezi Figura 5).

Teorema 2: Doua segmente simetrice fata de o dreapta sunt ongruente.

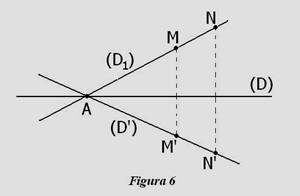Demonstratie: Pentru a construi simetrica unei drepte (D₁) fata de o axa de simetrie (D) (vezi Figura 6), se ia pe dreapta (D₁) un segment [MN] si se construieste simetricul lui, adica [M¢N¢

Dreapta pe care se gaseste segmentul [M¢N¢ este simetrica dreptei (D₁) in raport cu axa de simetrie pe care am luat-o. Dreapta (D₁) intersecteaza axa de simetrie in punctul A. Punctul A este propriul sau simetric; deci el trebuie sa se gaseasca si pe dreapta (D¢ pentru ca simetricele tuturor punctelor de pe dreapta (D₁) se afla pe dreapta (D¢ De aici reiese ca doua drepte simetrice in raport cu o dreapta se intersecteaza pe axa de simetrie. ð

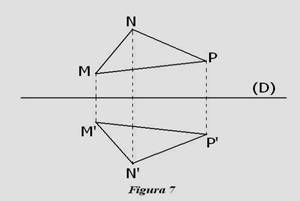
Teorema 3: Doua figuri, simetrice fata de o axa de simetrie sunt congruente (vezi Figura 7). ÿ

In spatiu, simetria fata de un punct se defineste la fel ca in geometria plana.

Rezolvarea problemelor cu ajutorul simetriei fata de un plan

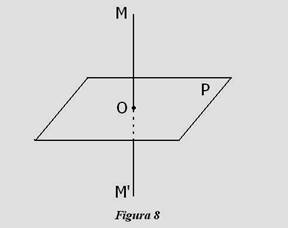Definitia 1: Fiind dat un plan P fix (vezi Figura 8), se spune ca doua puncte M si M¢ sunt simetrice fata de planul P, daca planul P este perpendicular pe segmentul [MM¢ in mijlocul acestuia.

Planul P se numeste plan de simetrie.

Din definitia de mai sus rezulta ca, pentru a construi simetricul unui punct M fata de un plan dat P, se duce din M perpendiculara MO pe planul P, apoi se ia pe prelungirea acestei perpendiculare segmentul [OM¢ , cu:

OM¢=OM

Metoda simetriei consta in faptul ca, in rezolvarea unor probleme de geometrie ne folosim de simetrie pentru a reduce problema data la una a carei rezolvare este cunoscuta sau se poate rezolva mai usor. Rezolvarea problemei noi aduce dupa sine si rezolvarea problemei initiale.

Exemplele urmatoare pun in evidenta aplicarea metodei simetriei.

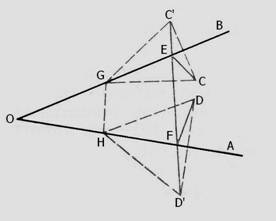
Problema 1: In interiorul unghiului AOB se dau doua puncte: C si D. Sa se gaseasca pe latura [OA] a unghiului dat un punct F si pe latura [OB] un punct E, in asa fel incat linia franta CEFD sa fie cea mai scurta posibila

Solutie: Mai intai construim figura (vezi figura de mai jos), care se compune din elementele date. Pentru a gasi punctele E si F vom proceda astfel: construim punctul C¢, simetricul lui C fata de OB, si punctul D¢, simetricul lui D fata de OA. Punctele C¢, D¢ si unghiul AOB inlocuiesc figura initiala, obtinand in felul acesta o figura noua. In loc de C si D, acum punctele C¢ si D¢ indeplinesc conditiile impuse de problema. Noua problema la care s-a redus problema initiala este: sa se gaseasca drumul cel mai scurt posibil intre C¢ si D¢ care sa atinga laturile [OB] si [OA] ale unghiului dat. Aceasta este o problema cunoscuta. Drumul cel mai scurt intre doua puncte este segmentul de dreapta care le uneste. In cazul nostru, segmentul [C¢D¢ intersecteaza laturile [OB] si [OA] in punctele E si F. Acestea sunt punctele cautate. Revenind la figura initiala, avem:

CE=C¢E

deoarece sunt lungimi de segmente simetrice fata de axa OB;

EF=EF, (latura comuna);

FD=FD¢

ca lungimi de segmente simetrice fata de axa OA;

CE+EF+FD=C¢E+EF+FD¢=C¢D¢

Linia franta CEFD este cea mai scurta. Oricare alte doua puncte luate pe laturile [OB] si [OA], in afara de E si F gasite mai sus, ne vor da o linie franta mai lunga decat CEFD. Intr-adevar, fie G si H doua puncte oarecare situate, respectiv, pe laturile [OB] si [OA]. Vrem sa aratam ca:

CE+EF+FD<CG+GH+HD

Observam ca, datorita simetriei, putem scrie:

CE+EF+FD=C¢E+EF+FD¢=C¢D¢ si

CG+GH+HD=C¢G+GH+HD¢

Insa, in patrulaterul C¢D¢HG, segmentul [C¢D¢ este mai scurt decat linia franta C¢GHD¢. Deci:

C¢D¢<C¢GHD¢ sau

CE+EF+FD<CG+GH+HD ð

Problema 2: Pe o masa de biliard care are forma unui dreptunghi sunt asezate doua bile. In ce directie trebuie lansata una dintre bile, care dupa ce a atins pe rand cele patru margini sa loveasca pe cea de-a doua bila?

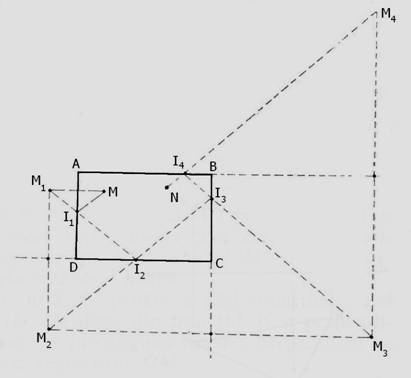
Solutie: Fie ABCD dreptunghiul care reprezinta forma masei de biliard (vezi figura de mai jos) si M si N pozitiile celor doua bile. Ne propunem sa lansam bila M. Aceasta dupa ce va lovi pe rand cele patru margini ale mesei, va trebui sa loveasca si bila N. Cunoscand legile reflexiei, am putea face acest lucru daca am cunoaste punctul de pe marginea AD a mesei de biliard pe care-l atinge bila M lansata, deoarece in felul acesta directia este determinata. Pentru a gasi acest punct procedam astfel:

Aflarea solutiei: Presupunem problema rezolvata. Fie I_1,I₂, I₃ si I₄, punctele pe unde bila de biliard atinge cele patru margini ale mesei. Observam ca bila M poate ajunge in punctul I₂, lansand-o din pozitia M₁, care este simetricul punctului M fata de latura [AD]. Cu alte cuvinte, putem inlocui punctul M cu M₁ si indepartam marginea AD. Acum punctul M₁ indeplineste conditiile lui M. De asemenea, bila M₁ poate ajunge in punctul I₃, lansand-o din punctul M₂, simetricul lui M₁ fata de latura [DC]. Deci inlocuim punctul M₁ cu M₂ si indepartam latura [DC]. La fel se observa ca bila M₂ poate ajunge in I₄, daca am lansa-o din punctul M₃, care este simetric cu punctul M₂ fata de latura [BC]. Deci inlocuim pozitia bilei M₂ cu M₃ si suprimam marginea BC. Bila M₃, la randul ei, poate sa loveasca bila N, daca am lansa-o din punctul M₄, simetricul lui M₃ fata de latura [AB]. Deci se poate inlocui punctul M₃ cu M₄ si indeparta latura [AB]. Punctul I₄ fiind astfel gasit, putem pleca din N prin reflexii succesive si gasim punctul I₁, care impreuna cu punctul M determina directia pe care trebuie lansata bila situata in punctul M pentru a lovi, dupa patru reflexii, bila N.

Constructia: Din cele spuse mai sus rezulta ca, pentru a gasi punctul I₁ care constituie cheia dezlegarii problemei, construim M₁ simetricul lui M fata de dreapta AD, M₂ simetricul lui M₁ fata de dreapta DC, M₃ simetricul lui M₂ fata de BC si punctul M₄ simetricul lui M₃ fata de AB. Unim M₄ cu N si gasim punctul I₄. Unind I₄ cu M₃, gasim punctul I₃; unind I₃ cu M₂, gasim punctul I₂ si, in cele din urma, unind pe I₂ cu M₁, gasim punctul I₁.

Demonstratie: Este cuprinsa in aflarea solutiei.

Discutia: Pentru ca problema sa fie posibila trebuie ca dreapta M₄N sa intersecteze latura [AB] intr-un punct situat intre varfurile A si B ale dreptunghiului care reprezinta forma mesei de biliard. ð

Problema 3: Intr-un triunghi isoscel, suma distantelor de la un punct oarecare al bazei la celelalte doua laturi este constanta

Solutie: Fie ABC triunghiul isoscel dat (vezi figura de mai jos), iar D un punct oarecare pe latura [BC]. Din punctul D ducem perpendiculare pe laturile [AC] si [AB]. Se cere sa aratam ca:

DE+DF=constant

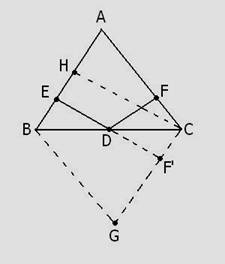Sa construim simetricul triunghiului ABC fata de latura [BC] ca axa de simetrie. Segmentul [DF] este congruent cu [DF¢ care la randul lui este in prelungirea segmentului [ED]. Intr-adevar, triunghiul ABC fiind isoscel, are:

ABCº ACB

Triunghiurile dreptunghice BDE si DFC avand cate un unghi ascutit de masuri egale, urmeaza ca ele au si celelalte doua unghiuri ascutite tot congruente, adica:

BDEº FDC

Insa:

FDCº CDF¢

prin simetrie. Deci:

BDEº CDF¢

Deoarece unghiurile BDE si CDF¢ sunt congruente si avand pozitia a doua unghiuri opuse la varf, urmeaza ca segmentul [DF¢ este in prelungirea segmentului [ED]. Pe de alta parte, segmentele [DF] si [DF¢ sunt congruente, pentru ca sunt simetrice fata de BC, deci: