 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
Punctul si dreapta incluse in plan. Proprietatile planelor simplu si dublu particulare.
Pozitii relative ale dreptei fata de plan. Reguli de vizibilitate
1. Punctul si dreapta incluse in plan
Fiind dat un plan oarecare se cere sa se verifice daca un punct, definit prin coordonate, apartine acelui plan. O astfel de problema poate apare ori de cate ori se cere construirea de poligoane, drepte (paralele sau perpendiculare fata de o alta dreapta) intr-un plan deja definit. In toate aceste situatii este nevoie sa se aleaga puncte care indeplinesc conditia de a apartine planului. Conditia ca un punct sa apartina unui plan se formuleaza astfel:
T3 |
Un punct apartine unui plan daca apartine unei drepte cuprinsa in acel plan. |
Observatii
1. In cazul unui plan dublu particular conditia de mai sus se poate reformula dupa cum urmeaza:
T3 - 1 |
Un punct apartine unui plan dublu particular (definit ca locul geometric al punctelor de abscisa / departare / cota data) daca respectiv abscisa / departarea / cota sa este egala cu cea a planului. |
|
|
Fig. 1 Fig. 2
In figurile 1 si 2
punctul M(10, 30, 30) apartine planului de front [F] caracterizat prin
departarea y = 30 deoarece y M
= y [F]. Punctul N(35, 10, 13) nu
apartine planului [F] deoarece y N
y [F]. Astfel
segmentul ![]() intersecteaza
planul de front in punctul M.
intersecteaza
planul de front in punctul M.
2. In cazul unui plan simplu particular conditia de mai sus se poate reformula dupa cum urmeaza:
T3 -2 |
Un punct apartine unui plan simplu particular daca o proiectie a sa apartine urmei inclinate omonime a planului. |
|
|
Fig. 3 Fig. 4
In figurile 3 si 4 punctul B(10, 18, 30)
apartine planului de capat [P] deoarece proiectia verticala
b' apartine urmei inclinate (urma verticala) a planului. Spunem
ca: daca [P] [V] si ![]() (PV) T
(PV) T ![]() [P]. In aceleasi figuri punctul A(28, 18, 30) nu
apartine planului [P]. Segmentul
[P]. In aceleasi figuri punctul A(28, 18, 30) nu
apartine planului [P]. Segmentul ![]() este un segment de dreapta fronto-orizontala care
intersecteaza planul [P] in
este un segment de dreapta fronto-orizontala care
intersecteaza planul [P] in ![]() .
.
b) Dreapta inclusa in plan
Problema apartenentei unei drepte la un plan dat intervine atunci cand se doreste construirea unui poligon sau a unui contur (inchis sau deschis) compus din segmente de dreapta si / sau arce de cerc, respectand conditia ca acesta sa fie plan.
Pentru a exprima conditia de apartenenta a unei drepte la un plan se foloseste reciproca definitiei planului. Deci, o dreapta apartine unui plan daca doua dintre punctele sale sunt cuprinse in plan
Grafic, in epura, aceasta conditie se aplica folosind punctele semnificative ale unei drepte, adica urmele sale (orizontala, verticala, laterala) si formularea conditiei anterioare devine cea de mai jos:
T4 |
O dreapta apartine unui plan daca urmele sale apartin urmelor de acelasi nume (omonime) ale planului. |
Observatie importanta: in cazul planelor simplu si dublu particulare este mai simplu sa se verifice apartenenta la plan a oricare doua puncte ale dreptei.
Exemplul
nr. 1: Fie planul vertical [Q] ([Q] [H]) definit prin punctele
Qx(40, 0, 0) si Qy(0, 40, 0). Se cere sa se verifice daca
segmentul ![]() apartine planului [Q]. In figurile 5 si 6 sunt prezentate
schita spatiala si respectiv epura care contine
rezolvarea.
apartine planului [Q]. In figurile 5 si 6 sunt prezentate
schita spatiala si respectiv epura care contine
rezolvarea.
|
|
Fig. 5 Fig. 6
Varianta
1) Deoarece ![]() si
si ![]() definesc o
dreapta oarecare, aceasta are trei urme:
definesc o
dreapta oarecare, aceasta are trei urme: ![]() - urma orizontala,
- urma orizontala, ![]() - urma verticala si
- urma verticala si ![]() - urma laterala, dintre care cu usurinta
se determina H(h, h', h'') si W(w, w', w''). Din schita
spatiala se observa ca urma orizontala apartine
urmei orizontale (Q h) a planului si urma laterala W
apartine urmei laterale (Q W) a planului. In epura
- urma laterala, dintre care cu usurinta
se determina H(h, h', h'') si W(w, w', w''). Din schita
spatiala se observa ca urma orizontala apartine
urmei orizontale (Q h) a planului si urma laterala W
apartine urmei laterale (Q W) a planului. In epura ![]() (Q h) si
(Q h) si ![]() (Q W) deci dreapta (CD) apartine planului [Q].
(Q W) deci dreapta (CD) apartine planului [Q].
Varianta
2) In mod direct se constata ca ![]() si
si ![]() (proiectiile orizontale ale extremitatilor
segmentului) apartin urmei orizontale (Qh) a planului, deci
cele doua puncte sunt in plan si in consecinta dreapta (CD)
apartine planului.
(proiectiile orizontale ale extremitatilor
segmentului) apartin urmei orizontale (Qh) a planului, deci
cele doua puncte sunt in plan si in consecinta dreapta (CD)
apartine planului.
Exemplul nr. 2: Fie planul de nivel [N] de cota zN = 30 mm si dreapta definita de punctele E(28,5; 8,5; 30) si F(11,5; 22,5; 30). Sa se verifice daca dreapta astfel definita apartine planului [N] (figurile 7 si 8).
Varianta
1) In acest caz este evident ca punctele ![]() si
si ![]() apartin planului
de nivel [N] deoarece zE = zF =z [N] = 30 mm
si deci dreapta determinata de ele este o dreapta de nivel.
apartin planului
de nivel [N] deoarece zE = zF =z [N] = 30 mm
si deci dreapta determinata de ele este o dreapta de nivel.
Varianta
2) Se poate verifica apartenenta dreptei (EF) la plan determinand cele
doua urme ale dreptei: V(v, v', v'') si W(w, w', w'') (o dreapta
de nivel nu are urma orizontala). Se constata ca ![]() (proiectia
verticala a urmei verticale
(proiectia
verticala a urmei verticale ![]() ) apartine urmei verticale (N V ) a planului:
) apartine urmei verticale (N V ) a planului:
![]() (NV) si
(NV) si ![]() (proiectia
laterala a
(proiectia
laterala a ![]() ) apartine urmei laterale (N W) a planului:
) apartine urmei laterale (N W) a planului: ![]() (N W).
(N W).
|
|
Fig. 7 Fig. 8
2. Proprietatile planelor simplu si dublu particulare
a) Proprietatile planelor simplu particulare
Datorita pozitiei lor in spatiu planele simplu particulare au urmatoarele proprietati, numite proprietati metrice. In cele ce urmeaza ele sunt prezentate pentru planul fronto-orizontal.
|
|
Fig. 9 Fig. 10
P6 |
Orice punct cuprins in planul fronto-orizontal are proiectia laterala situata pe urma laterala (inclinata) a planului. |
 Aceasta proprietate este o consecinta a pozitiei
planului fronto-orizontal (perpendicular pe planul lateral). Proiectanta
oricarui punct din plan fata de planul lateral este o
dreapta a planului fronto-orizontal si intersecteaza [W] intr-un
punct ce apartine atat planului lateral cat si planului
fronto-orizontal, deci intr-un punct apartinand urmei laterale a planului.
In figurile 9 si 10 fiecare dintre punctele A(35, 30, 5), B (10, 30, 5)
si C(10, 5, 30) apartin planului fronto-orizontal definit prin
punctele PZ (0, 0, 40) si PY(0, 40, 0) pentru
ca proiectiile lor laterale
apartin urmei laterale.
Aceasta proprietate este o consecinta a pozitiei
planului fronto-orizontal (perpendicular pe planul lateral). Proiectanta
oricarui punct din plan fata de planul lateral este o
dreapta a planului fronto-orizontal si intersecteaza [W] intr-un
punct ce apartine atat planului lateral cat si planului
fronto-orizontal, deci intr-un punct apartinand urmei laterale a planului.
In figurile 9 si 10 fiecare dintre punctele A(35, 30, 5), B (10, 30, 5)
si C(10, 5, 30) apartin planului fronto-orizontal definit prin
punctele PZ (0, 0, 40) si PY(0, 40, 0) pentru
ca proiectiile lor laterale
apartin urmei laterale.
|
Definitie |
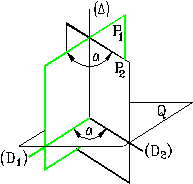
Unghiul dintre doua plane concurente este unghiul masurat intr-un plan perpendicular pe dreapta lor de intersectie si for-mat de dreptele de intersectie dintre plane si planul normal. |
Fig. 11
In figura 11 unghiul a din spatiu dintre planele [P1] si [P2] se masoara in planul [Q] D [P1] ∩ [P2], intre dreptele (D1) si (D2), (D1) [P1] ∩ [Q] si (D2) [P2] ∩ [Q].
Pe baza acestei defintii se poate enunta urmatoarea proprietate a planului fronto-orizontal:
|
P7 |
Unghiurile pe care le formeaza in spatiu planul fronto-orizontal cu planul vertical si cu planul orizontal sunt unghiurile dintre urma laterala (PW) si axele (OZ) si respectiv (OY'). |
Se constata din figura 9 ca unghiul dintre planul fronto-orizontal [P] si planul vertical este unghiul masurat in planul [W] intre dreptele de intersectie (OZ) [P] ∩ [V] si (PW) [P] ∩ [W]. In epura se rega-seste acelasi unghi intre (OZ) si (PW).
b) Proprietatile planelor dublu particulare
Proprietatile planelor dublu particulare reprezinta particularizari ale proprietatilor planelor simplu particulare.
Astfel, pentru planul de profil [R] [H] si [R] [V] T [R] [W] proprietatile P6 si P7 devin:
P8 |
Orice punct cuprins intr-un plan de profil are proiectiile verticala si orizontala situate pe urmele omonime (cu acelasi nume) ale planului. |
|
P9 |
Unghiurile pe care le formeaza in spatiu planul de profil cu planul vertical si cu planul orizontal sunt unghiurile pe care le formeaza urma verticala (PV) si urma orizontala (PH) cu axa (OX). |
Pentru ca planul de profil este paralel cu planul lateral, acestor doua proprietati li se adauga o a treia:
P10 |
Orice figura cuprinsa intr-un plan de profil se proiecteaza in adevarata marime pe planul lateral. |
|
|
Fig. 12 Fig. 13
In figurile 12 si 13 este exemplificat cazul unui plan de profil [R] care contine un cerc de centru C(30, 25, 23) de raza r = 14 mm. Toate punctele semnificative ale cercului - centrul C si punctele diametral opuse 1, 2, 3, 4 - apartin planului si cercul se proiecteaza in adevarata marime pe planul lateral dar deformat pe planul orizontal (ca segmentul (2-4) si pe planul vertical ca segmentul (1' -3').
3. Pozitii relative ale dreptei fata de plan
In raport cu un plan o dreapta se poate gasi in una dintre urmatoarele pozitii relative: a) paralelism; b) concurenta. Perpendicularitatea unei drepte fata de un plan este un caz particular al concurentei (intersectiei) dintre o dreapta si un plan (unghiul dintre dreapta si plan fiind de 90
a) Dreapta paralela cu planul
Fiind dat un plan oarecare si un punct exterior lui, se cere sa se construiasca prin punct o dreapta paralela cu planul. Rezolvarea se bazeaza pe teorema cunoscuta din geometria in spatiu:
T5 |
O dreapta este paralela cu un plan daca este paralela cu o dreapta continuta in plan. |
Observatie: pentru ca intr-un plan se pot construi / alege o infinitate de drepte, rezulta ca se poate construi o infinitate de drepte paralele cu planul dat, ceea ce inseamna ca formularea problemei permite o infinitate de solutii. Pentru a obtine o solutie unica este nevoie si de o a doua conditie care sa precizeze directia dreptei ce indeplineste conditia de perpendicularitate.
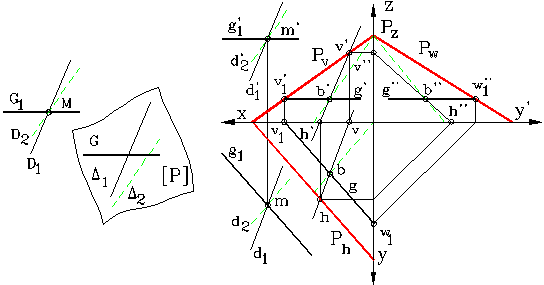
Fig. 14
In
figura 14 este prezentata o schema intuitiva si
constructia grafica a unei drepte paralele cu un plan determinat prin
urmele sale. Asa cum s-a aratat anterior, printr-un punct exterior
unui plan se pot construi o infinitate de drepte paralele cu planul dat,
fiecare din ele fiind paralela cu o dreapta continuta in
plan. Astfel, daca in planul [P] se aleg dreptele (D ) si (D ), prin ![]() [P] se pot construi doua drepte (D1) D ) si (D2) D ) care astfel sunt paralele
cu [P].
[P] se pot construi doua drepte (D1) D ) si (D2) D ) care astfel sunt paralele
cu [P].
Problema
construirii unei drepte paralele la un plan are solutie unica doar
daca se impune o con-ditie suplimentara (directia dreptei
in spatiu, apartenenta ei la un alt plan etc.). In figura 14 este
exem-plificata constructia prin ![]() a unei drepte (G1) care: a) este paralela cu
[P] si b) este o orizontala, adica (G1) [H].
a unei drepte (G1) care: a) este paralela cu
[P] si b) este o orizontala, adica (G1) [H].
Pentru a fi paralela cu [P], (G1) trebuie sa fie paralela cu o dreapta din [P] iar pentru a fi orizontala, trebuie ca insasi dreapta din plan sa fie orizontala.
Prin
![]() [P] s-a construit dreapta (G). Ea este o orizontala pentru
ca :
[P] s-a construit dreapta (G). Ea este o orizontala pentru
ca :
1) proiectia
verticala (g') a fost construita prin ![]() paralela cu axa
(OX):
paralela cu axa
(OX): ![]() (g') (OX);
(g') (OX);
2) proiectia
laterala (g'') a fost construita prin ![]() paralela cu axa
(OY'):
paralela cu axa
(OY'): ![]() (g'') (OY');
(g'') (OY');
3) proiectia
orizontala (g) a fost construita prin ![]() paralela cu urma
orizontala a planului:
paralela cu urma
orizontala a planului:![]() (g) (Ph);
(g) (Ph);
Dreapta (G) astfel construita este o dreapta continuta in planul [P] deoarece:
1) contine punctul B, B (G) iar acesta apartine planului;
2) urma sa verticala V1 (v1, v1' ) are proiectia verticala v1' situata pe urma verticala a planului, (PV), ceea ce inseamna ca V1 apartine planului [P]. Astfel (G) are doua puncte ce apartin planului [P] deci este continuta in acesta.
Prin urmare dreapta (G1) construita prin![]() paralela cu (G) este paralela cu [P].
paralela cu (G) este paralela cu [P].
De asemenea este paralela cu [P] dreapta (D2)
construita prin![]() paralela cu dreapta (VH) din plan.
paralela cu dreapta (VH) din plan.
b) Dreapta concurenta cu planul
O dreapta intersecteaza un plan daca are doar un punct comun cu planul respectiv. Gasirea acestui punct comun este foarte usoara in cazul intersectiei dreptelor cu planele simplu si dublu particulare datorita proprietatilor acestora. Problema intersectiei dintre o dreapta si un plan oarecare se poate rezolva fie direct, fie transformand planul oarecare intr-un plan simplu particular. Ambele rezolvari presupun notiuni suplimentare.
1) Intersectia dintre o dreapta si un plan simplu particular
Fie planul vertical ([Q] [H]) definit prin punctele QX (40, 0, 0), QY
(0, 40, 0) si segmentul ![]() . Din figurile 15 si 16 se observa ca punctul D(20, 20,
20) este punctul de intersectie dintre planul [Q] si segmentul
. Din figurile 15 si 16 se observa ca punctul D(20, 20,
20) este punctul de intersectie dintre planul [Q] si segmentul ![]() deoarece el
apartine atat segmentului cat si planului.
deoarece el
apartine atat segmentului cat si planului.
Determinarea grafica, in epura, a punctului de intersectie se bazeaza pe rationamentul de mai jos.
1) Deoarece [Q] [H], punctele cuprinse in plan au proiectiile orizontale situate pe (Qh), urma sa orizontala.
2) Un punct de intersectie dintre segmentul de dreapta si plan este cel a carui proiectie orizontala apartine concomitent proiectiei orizontale a segmentului si urmei orizontale a planului. Aceasta conditie o inde-plineste doar punctul notat d care rezulta din intersectia (ab) si (Q h), adica d (ab) ∩ (Q h).
3) Deoarece punctul de intersectie dintre plan si segmentul de dreapta este un punct al segmentului, el va avea proiectia verticala d' situata pe proiectia verticala a segmentului (a'b') iar proiectia laterala d'' apartine proiectiei laterale a segmentului (a''b'').
|
|
Fig. 15 Fig. 16
2) Intersectia dintre o dreapta si un plan dublu particular
In
figurile 17 si 18 este prezentata determinarea punctului de
intersectie dintre planul de nivel [N] avand cota z[N] = 20 mm
si segmentul ![]() . Rationamentul este
asemanator cu cel prezentat anterior.
. Rationamentul este
asemanator cu cel prezentat anterior.
1) Deoarece [N] [H], atunci toate punctele cuprinse in plan au proiectiile verticale situate pe urma verticala (N V ) a planului iar proiectiile laterale apartin urmei laterale a planului, (N W).
2) Un punct comun al segmentului de dreapta si al planului este cel a carui proiectie verticala apartine concomitent proiectiei verticale a segmentului si urmei verticale a planului. Aceasta conditie o indeplineste doar punctul notat q' care rezulta din intersectia (m'p') si (N V ), adica: q' (m'p') ∩ (N V ).
3) Deoarece punctul de intersectie dintre plan si segmentul de dreapta este punct al dreptei, el satisface conditiile: proiectia orizontala q apartine proiectiei orizontale a segmentului (mp) si proiectia laterala q'' apartine proiectiei laterale a segmentului (m''p'').
|
|
Fig. 17 Fig. 18
i
4. Reguli de vizibilitate
Reprezentarea in tripla proiectie ortogonala are la baza conventia ca un observator studiaza un obiect din spatiu privindu-l dupa trei directii, normale la planele de proiectie si ale caror sensuri sunt indicate in figura 19. De exemplu pentru a obtine proiectia pe planul vertical directia de privire este in sens invers sensului
pozitiv al axei OY. Este evident ca dintre punctele obiectului studiat, o parte sunt vizibile pentru observator iar altele invizibile.Regula dupa care se determina vizibilitatea unui punct din spatiu fata de alte puncte intr-o proiectie este:
|
RV 1 |
Daca doua sau mai multe puncte au proiectiile pe un plan confundate, este vizibil acel punct al carui distanta fata de plan este mai mare. |
|
|
In fig. 19 varfurile 1 si 5 ale parale-lipipedului 1-2-3-4-5-6-7-8 au proiectii verticale confundate dar vizibil este varful 1 deorece el este mai apropiat de observator (sau altfel spus distanta sa fata de planul vertical este mai mare decat distanta varfului 5 fata de acelasi plan).
In problemele de intersectie dintre drepte si plane este necesar sa se determine vizibilitatea dreptei in raport cu planul pe care il intersec-teaza, asa cum se arata in figurile 15, 16 si 17, 18.
Fig. 19
APLICATIE
|
|
Fie placa ABC si
segmentul ![]() a ca-ror pozitie reciproca este cea din fig.
20. Sa se determine grafic punctul lor de intersectie si sa
se justifice vizibilitatea segmentului
a ca-ror pozitie reciproca este cea din fig.
20. Sa se determine grafic punctul lor de intersectie si sa
se justifice vizibilitatea segmentului ![]() in raport cu placa. Se dau coordonatele: A(5, 5, 5), B(13,
35, 10), C(45, 10, 30), M(45, 20, 0), N(15, 20, 30).
in raport cu placa. Se dau coordonatele: A(5, 5, 5), B(13,
35, 10), C(45, 10, 30), M(45, 20, 0), N(15, 20, 30).
REZOLVARE
Se observa ca ![]() este un segment de
front (y M = y N = 20) iar placa apartine unui plan
de capat (proiectiile a', b' si c' sunt coliniare).
Datorita faptu-lui ca planul placii este un plan simplu
particular, punctul de intersectie I (i, i', i'') are proiectia
verti-cala i' in punctul de intersectie al proiectiei ver-ticale
(m"n") cu urma planului (a'c'). Celelalte doua proiectii i si
i'' se determina la intersectia liniilor de ordine cu
proiectiile (mn) si (m''n''), deoarece punctul I apartine
segmentului
este un segment de
front (y M = y N = 20) iar placa apartine unui plan
de capat (proiectiile a', b' si c' sunt coliniare).
Datorita faptu-lui ca planul placii este un plan simplu
particular, punctul de intersectie I (i, i', i'') are proiectia
verti-cala i' in punctul de intersectie al proiectiei ver-ticale
(m"n") cu urma planului (a'c'). Celelalte doua proiectii i si
i'' se determina la intersectia liniilor de ordine cu
proiectiile (mn) si (m''n''), deoarece punctul I apartine
segmentului ![]() .
.
Fig. 20
Vizibilitatea in proiectia orizontala se stabileste pe baza urmatoarelor rationamente:
- de la n la punctul de concurenta aparenta cu latura (cb) segmentul (nm) este evident vizibil;
- punctului de
concurenta aparenta (1=2) ii corespund doua puncte din
spatiu: punctul 1 aparti-nand laturii ![]() si punctul 2
apartinand segmentului
si punctul 2
apartinand segmentului![]() , proiectiile lor verticale fiind notate cu 1' si
2'. Deoarece cota punctului 1 este mai mare decat cota punctului 2 (z 1
> z 2) rezulta ca va fi vizibila latura (cb) sau,
altfel spus, segmentul (nm) devine invizibil de la punctul de concurenta
aparenta;
, proiectiile lor verticale fiind notate cu 1' si
2'. Deoarece cota punctului 1 este mai mare decat cota punctului 2 (z 1
> z 2) rezulta ca va fi vizibila latura (cb) sau,
altfel spus, segmentul (nm) devine invizibil de la punctul de concurenta
aparenta;
- segmentul (nm) se mentine invizibil pana cand intersecteaza (strapunge) placa in i si astfel devine din nou vizibil.
Vizibilitatea in
proiectia laterala se
stabileste in mod asemanator, comparand abscisele punctului 1 ce
apartine laturii ![]() si punctului 3 ce
apartine segmentului
si punctului 3 ce
apartine segmentului ![]() .
.
BIBLIOGRAFIE
1. VRACA Ileana DESEN INDUSTRIAL Editura Tehnica Bucuresti 1984 (Cap. 7 Reprezentarea, sectionarea si intersectarea corpurilor geometrice uzuale pag. 75 - 77)
2. PRECUPETU Paul, DALE Constantin PROBLEME DE GEOMETRIE DESCRIPTIVA CU APLICATII IN TEHNICA Editura Tehnica Bucuresti 1987 (Cap. 1.3 Planul pag. 39 -58)
Copyright © 2024 - Toate drepturile rezervate