Coduri ciclice

Coduri ciclice

Codurile ciclice sunt coduri bloc in care cele n simboluri din cuvant sunt considerate ca fiind coeficientii unui polinom de grad n-1:

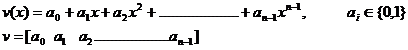
Cuvantul de cod fiind identificat cu un polinom, asupra lui se pot efectua operatii matematice mai complexe, pe langa operatia de adunare si inversa ei fiind definita si operatia de inmultire si inversa ei.

Ideea de baza a mecanismului de detectie sau corectie consta in alegerea polinoamelor divizibile cu un polinom dat g(x) ca fiind cuvinte de cod (cuvinte cu sens). Polinomul g(x) se numeste polinom generator al codului. Daca in procesul de transmisiune nu s-au introdus erori, polinomul care reprezinta cuvantul receptionat, divizat cu g(x) va da un rest nul. Daca s-au introdus erori restul va fi diferit de 0.

Existenta unui rest diferit de 0 este un criteriu pentru detectia erorilor. Daca din restul obtinut se pot trage concluzii asupra pozitiei in care s-au introdus erorile, codul permite corectarea lor.

Codul se numeste ciclic deoarece daca este un cuvant de cod, atunci si toate cuvintele de forma sunt cuvinte de cod. Cu alte cuvinte, orice permutare ciclica a unui cuvant de cod conduce tot la un cuvant de cod.

Presupunand ca numarul de simboluri dintr-un cuvant este n, rezulta ca se pot forma 2ⁿ cuvinte. Dintre acestea se considera ca 2^k cuvinte sunt cuvinte de cod (cu sens). Altfel spus, obtinem m=n-k simboluri de control, servind la detectia sau corectia erorilor.

Consideram ca multimea tuturor cuvintelor (ce formeaza o algebra) este generata de un polinom p(x) de grad n de forma , iar multimea cuvintelor cu sens (ce formeaza un ideal) este generata de un polinom g(x) numit polinom generator, de grad m, de forma:

Se poate arata ca intre cele doua polinoame p(x) si g(x) exista relatia: , unde .

Orice cuvant de cod poate fi exprimat printr-o combinatie liniara a urmatorilor k vectori independenti : .

Cu alte cuvinte, un cuvant de cod se gaseste in spatiul linie al matricii generatoare G:

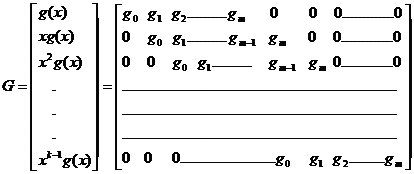
Polinomul g(x) de grad m a fost completat pana la gradul n-1 cu componente nule. Rezulta ca prin cunoasterea polinomului generator g(x) se determina matricea generatoare G, respectiv structura codului ciclic. Matricea generatoare G are k vectori linie liniar independenti cu care se pot forma 2^k combinatii liniare, respectiv 2^k cuvinte de cod.

Codarea cuvintelor de cod ca elemente in multimea cuvintelor cu sens generata de g(x)

Fie g(x) polinomul generator al codului, de grad m, si i(x) polinomul de grad k=n-m care are drept coeficienti simbolurile de informatie:

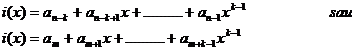
A) Determinarea simbolurilor de control folosind g(x)

Polinomul simbolurilor de control se noteaza cu :

Deci cuvantul de cod se scrie :

Impartind expresia de mai sus prin g(x) rezulta:

Termenul reprezinta termenii cuvantului de cod care contin informatia transmisa. Ultimul termen se rescrie: , unde q(x) reprezinta catul (de grad < k ), iar r(x) reprezinta restul (de grad < m) impartirii lui la g(x).

.

Astfel, polinomul simbolurilor de control se obtine prin divizarea polinomului simbolurilor de informatie multiplicat cu x^m prin g(x). In acest fel se obtine un cuvant de cod SISTEMATIC.

B) Ce-a de-a doua metoda pentru determinarea simbolurilor de control se bazeaza pe introducerea matricii generatoare G definita anterior, avand k linii si n coloane. Codarea are loc cu ajutorul relatiei :

v=iG , unde    i=[a_m a_m+1 a_m+k-1].

Codarea cuvintelor de cod cu ajutorul polinomului de control h(x)

Se pleaca de la relatia potrivit careia v(x) este multiplu de g(x):

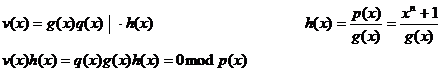
Sau, sub forma matriceala: Hv^T= 0, unde matricea H are forma (m linii, n coloane):

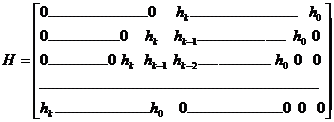
Elementele h_i sunt coeficientii polinomului completat pana la gradul n-1 cu coeficienti nuli. Matricea H are m linii liniar independente astfel incat relatia Hv^T= 0 este echivalenta cu m ecuatii liniare ce determina cele m simboluri de control in functie de cele k simboluri de informatie.

De asemenea, se poate arata ca GH^T=HG^T.

Exemplu:

Se transmit N=16 mesaje pe un canal afectat de perturbatii, utilizand un cod ciclic corector de o eroare.

Se pot determina parametrii codului: pentru a transmite 16 mesaje sunt necesari cel putin 4 biti de informatie, adica:

gradul polinomului g(x) va fi deci 3

rezulta ca polinomul p(x) va avea forma:

Polinomul generator se poate alege dintre divizorii lui p(x):

Polinomul h(x) de grad k=m-n se determina din relatia p(x)=g(x)h(x)

Remember impartirea de polinoame J

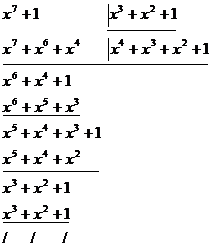
Codarea se poate realiza fie cu matricea G fie cu matricea H:

a) codarea cu matricea G

G(k,n)=G(4,7)

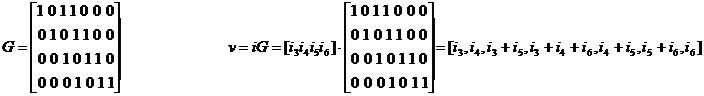
Cele 16 mesaje transmise vor fi codate corespunzator, ca in tabelul de mai jos:

b) Codarea cu matricea H

cuvantul de cod obtinut are o forma sistematica : v=[c₀ c₁ c₂ i₃ i₄ i₅ i₆]

se foloseste relatia de codare Hv^T=0

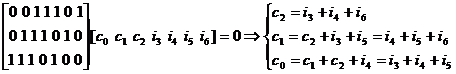
Se pot determina astfel cele 16 mesaje transmise:

Observatie: Spatiul cuvintelor cu sens este acelasi, indiferent de modul de codare, cu H sau G, insa difera corespondenta intre secventa informationala de 4 biti si cuvintele cu sens de 7 biti. De exemplu, cuvantul [1 1 1 1 1 1 1] corespunde in primul caz secventei informationale [1 1 0 1], iar in al doilea caz secventei [1 1 1 1].

Decodarea codurilor ciclice. Formarea corectorilor

Pentru un cuvant receptionat v'(x) se calculeaza corectorul :

indicele i indica tipul de eroare ε_i.

Se cauta intr-un tabel construit anterior corespondenta dintre corectorul z_i(x) si cuvantul eroare, respectiv ε_i(x).

Se calculeaza v(x)=v'(x)+ ε_i(x)

O metoda de a stabili tabelul mentionat anterior este sa se calculeze z_i pe baza relatiei

pentru diversi ε_i(x).

Se observa ca exista un singur tip de corector z_i pentru toate cuvintele eronate ε_i(x). Polinomul z(x) are gradul cel mult m-1, deci numarul acestor corectori este 2^m. Rezulta ca din multimea configuratiilor posibile de erori, respectiv de polinoame ε(x) in numar de 2ⁿ, numai cele care pot fi puse in corespondenta biunivoca cu corectorii z(x), adica un numar de 2^m configuratii de erori pot fi corectate.

Realizarea codarii si a decodarii pentru detectia erorilor prin circuite de multiplicare sau divizare

1) Codarea si decodarea prin multiplicare

v(x)=i(x)g(x)    in acest caz se obtine un cod nesistematic.

Demodularea se face prin divizare:

2) Codarea si decodarea prin divizare

in acest caz se obtine un cod sistematic.

Decodarea se face ca in cazul precedent prin divizare.

Codarea prin circuite de divizare

Fie circuitul secvential urmator, care foloseste celule binare notate cu C_i si sumatoare modulo 2 interioare:

Pentru analiza circuitului vom folosi un operator de intarziere notat cu D care reprezinta intarzierea de un tact pe care o introduce o celula binara.

Daca in registru se introduc coeficientii in ordine descrescatoare a indicilor: a_n, a_n-1, ., a₁, a₀, care corespund polinomului : , atunci secventa aplicata la intrare utilizand operatorul D poate fi pusa sub forma :

, cu interpretarea ca simbolul a₀ ajunge in prima celula de intrare dupa n tacte.

Pentru a evidentia operatia efectuata de circuit se defineste functia de transfer T ca fiind raportul dintre secventa de iesire Y si cea de intrare X:   

Pentru determinarea lui T se ia un caz particular: se presupune ca la intrare se aplica g(x). Primul simbol aplicat la intrare ajunge la iesire dupa m tacte (g_m=1). In acest moment Y=g_mD^m si la intrarea tuturor celulelor va fi simbolul 0. La tactul m+1 iesirile tuturor celulelor devin zero, deci Y=g_mD^m≠0 numai la tactul m, avand un singur termen:

Daca D^-1 tinde la x atunci se poate afirma ca circuitul realizeaza divizarea cu g(x).

In cazul general, cand polinomul de intrare este de grad n, catul divizarii se obtine la iesirea circuitului dupa n tacte, in timp ce restul va apare stocat in registru la tactul n.

Exemplu: n=7, m=3

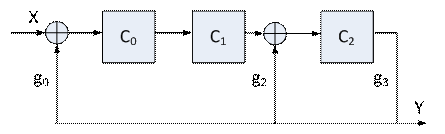
a)Daca se alege polinomul de intrare :

Regulile de calcul pentru succesiunea starilor (C' desemneaza starea celulei la momentul anterior):

tact IN (u) C0 C1 C2 OUT (y) Catul X4 X2 Restul X0 X1 X2

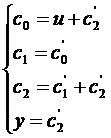
Catul :

Restul: 0

b)Daca se alege polinomul de intrare :

Regulile de calcul pentru succesiunea starilor :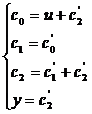

tact IN (u) C0 C1 C2 OUT (y) Catul X4 X2 Restul X0 X1 X2

Catul :

Restul: