Fitarea analitica a liniei de difractie

Fitarea analitica a liniei de difractie

Aceasta metoda foloseste in calcul functiile formei picului (Peak Shape Function), care pot fi diferentiate analitic in functie de fiecare parametru. Cele mai utilizate functii analitice pentru fitarea analitica a profilului liniei de difractie sunt: functia Gauss (G), functia Cauchy-Lorentz (C sau L), functia Lorentz modificata (ML), functia Lorentz intermediara (IL), functia Pearson VII (PVII), functia pseudo-Voigt (pV) si functia Voigt (V). In expresiile matematice ale acestor functii: . Cu ajutorul acestor functii nu se poate realiza intotdeauna o fitare corespunzatoare a intregului spectru de difractie, fara utilizarea unui numar mare de parametri. Aceasta conduce frecvent la pierderea unicitatii si la instabilitatea procedurii de fitare.

Prezentam in continuare expresiile matematice ale acestor functii, graficele acestora si formulele matematice de calcul ale largimilor profilului liniei de difractie, calculate cu ajutorul functiilor analitice.

Parametrul profilului liniei de difractie sau factorul de forma al liniei de difractie se defineste cu raportul .

Functia Gauss (G)

Expresia matematica a acestei functii este de forma:

sau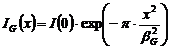

Daca functia Gauss este normata la unitate , atunci expresia matematica a acesteia devine:

, unde , .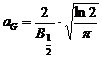

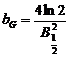In figura 1 este reprezentat graficul functiei Gauss si semnificatiile largimilor la semiinaltime , respectiv integrale

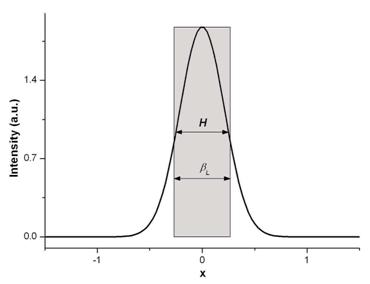
Figura 1. Graficul functiei Gauss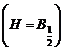

Largimea integrala a functiei Gauss este egala cu:

.

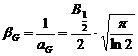Factorul de forma al functiei Gauss este egal cu .

Functia Gauss care descrie profilul unei linii de difractie este data de ecuatia:

.

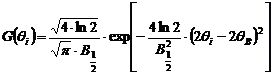Functia Cauchy (C) sau Lorentz (L)

Expresia matematica a acestei functii este de forma:

sau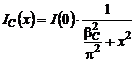

Daca functia Lorentz este normata la unitate , atunci expresia matematica a acesteia devine:

, unde , .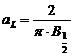

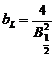In figura 2 este reprezentat graficul functiei Lorentz si semnificatiile largimilor la semiinaltime , respectiv integrale

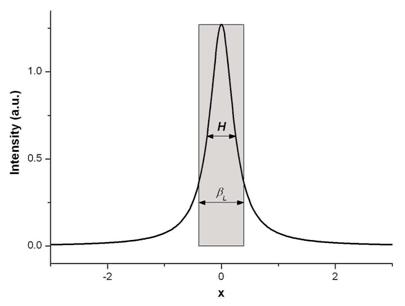
Figura 2. Graficul functiei Lorentz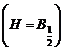

Largimea integrala a functiei Lorentz este egala cu:

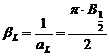
Factorul de forma al functiei Lorentz este egal cu .

Functia Lorentz care descrie profilul unei linii de difractie este data de ecuatia: .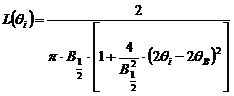

Nota. In ipoteza ca profilul liniei de difractie masurate pentru o proba reprezinta convolutia profilelor instrumental si fizic (Taupin, 1973): , largimea integrala a profilului liniei de difractie se poate calcula cu formulele:

(9), daca toate profilele au forma descrisa de functia Cuachy;

(10), daca toate profilele au forma descrisa de functia Gauss.

Functia Lorentz modificata

Expresia matematica a acestei functii normate la unitate este de forma:

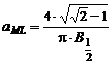, unde si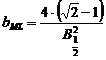

Functia Lorentz modificata care descrie profilul unei linii de difractie este data de ecuatia:

.

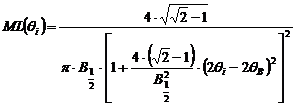In figura 3 sunt reprezentate graficele functiei Lorentz modificata si functiei Lorentz.

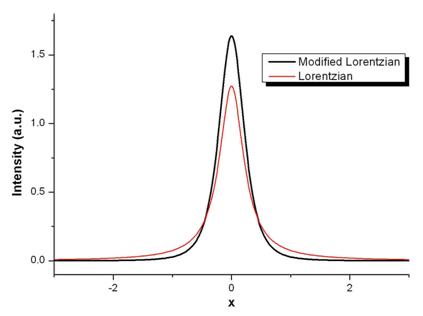
Figura 3. Graficele functiilor Lorentz modificata, respectiv Lorentz

Functia Lorentz intermediara

Expresia matematica a acestei functii normate la unitate este de forma:

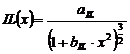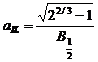,unde si .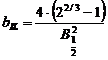

Functia Lorentz intermediara care descrie profilul unei linii de difractie este data de ecuatia:

.

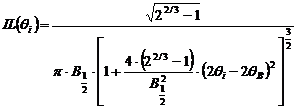In figura 4 sunt reprezentate graficele functiei Lorentz intermediara si functiei Lorentz.

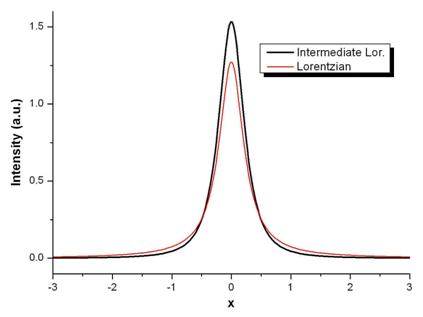
Figura 4. Graficele functiilor Lorentz intermediara, respectiv Lorentz

In majoritatea cazurilor liniile de difractie masurate sunt descrise bine cu ajutorul functiilor Cauchy sau Gauss (Klug si Alexander, 1974; Zoung si Wiles, 1982). In unele cazuri, pentru descrierea profilului liniilor de difractie cu radiatii X sau cu neutroni, trebuie sa se foloseasca functiile Voigt sau pseudo-Voigt (Wertheim si altii, 1974) sau functia Pearson-VII (Hall si altii, 1977).

Functia Pearson VII (P7):

Expresia matematica a acestei functii normate la unitate este de forma:

,

unde 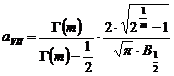si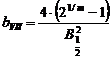

Functia Pearson VII care descrie profilul unei linii de difractie este data de ecuatia:

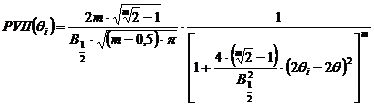
In figura 5 este reprezentat graficul functiei Pearson VII.

Figura 5. Graficul functiei Pearson VII

Functia pseudo-Voigt (pV)

Reprezinta o combinatie liniara a unei functii Lorentz cu o functie Gauss , avand aceeasi largime la jumatatea inaltimii maxime si se defineste cu expresia matematica:

,

Functia depinde de doi parametrii care caracterizeaza profilul liniei de difractie: .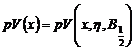

In figura 6 sunt reprezentate graficele functiei pseudo-Voigt (pV) pentru diferite valori ale coeficientului . Pentru , functia pseudo-Voigt trece in functia Gauss, iar pentru functia pseudo-Voigt trece in functia Lorentz.

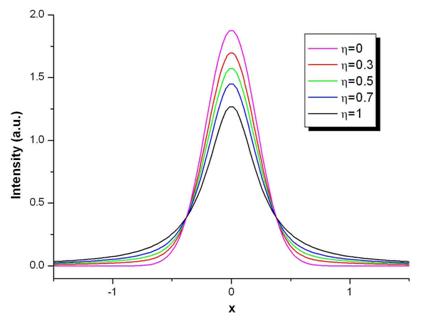
Figura 6. Graficul functiei pseudo-Voigt

Largimea integrala a functiei , normata la unitate, este egala cu inversul valorii maxime a acestei functii: .

Daca functia este multiplicata cu o constanta (intensitatea integrala), atunci largimea integrala se calculeaza cu formula:

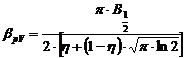
Functia pseudo-Voigt inlocuieste perechea de parametrii , care caracterizeaza functiile Lorentz si Gauss, cu perechea de parametrii , care caracterizeaza functia pseudo-Voigt.

In programul FulProff expresia matematica folosita pentru functia Pseudo-Voigt este de forma:

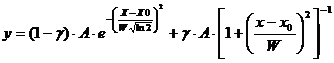
in care si sunt parametrii de fitare. In acest caz, 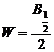, iar reprezinta valoarea unghiului la care este centrata functia. Parametrul reprezinta contributia functiei Lorentz la functia pseudo-Voigt.

Constrangerile impuse functiei pseudo-Voigt sunt urmatoarele:

Largimile tuturor functiilor la semiinaltime au aceeasi valoare.

.

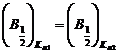Contributiile functiei Lorentz pentru radiatiile si sunt egale.

Functia Voigt (V)

Reprezinta convolutia unei functii Gauss cu o functie Lorentz:

,

in care functiile Lorentz si Gauss au largimile la jumatatea inaltimii maxime egale: .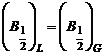

Expresia matematica a functiei Voigt folosita uzual (Langford, 1978) este:

,

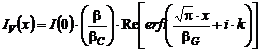unde . Functia complexa de eroare se defineste cu formula , in care este conjugata functiei complexe de eroare.

In figura 7 este prezentat graficul functiei Voigt, descrisa de ecuatia , unde si pentru mai multe valori ale parametrilor si .

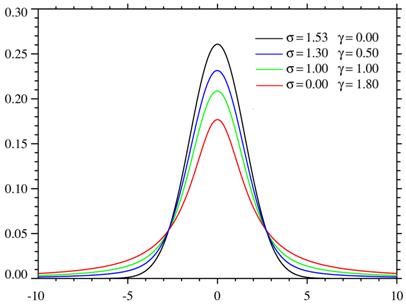
Figura 7. Graficul functiei Voigt pentru diferite valori ale parametrilor si Curba neagra corespunde graficului functiei Gauss , iar cea rosie - graficului functiei Lorentz

Largimea integrala a functiei Voigt se calculeaza cu formula (Schoening, 1965: (9a)

Halder si Wagner (1966) au propus o formula aproximativa de calcul care permite calculul rapid al largimii integrale:

(10a).

In cazul in care profilele sunt descrise de doua functii Voigt sau de o functie Voigt si o alta functie, largimea integrala se calculeaza cu formulele (9) si (10)

Functia Voigt este o functie care depinde de largimea integrala a functiei Lorentz si de largimea integrala a functiei Gauss :

,

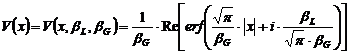unde .