Treapta de potential

Treapta de potential

Consideram miscarea unidimensionala a unei particule in sensul pozitiei axei Ox intr-un camp de forta in care poseda energia potentiala.

Din punctul de vedere elastic asupra particulei se exercita o forta de respingere in unde energia potentiala prezinta un salt finit Vom considera cazul in care energia particulei este mai mare decat inaltimea treptei de potential , situatie care in cazul clasic corespunde unor particule care trec dincolo de

Deoarece putem considera functia de unda factorizata :

unde este solutie a ecuatiei Schrödinger atemporale:

In regiunea si ecuatia devine:

sau

Particula fiind libera, energia ei cinetica si putem nota a. i. ecuatia va admite solutia generala :

, care conduce la

Primul termen este o unda plana progresiva de amplitudine A, asociata cu particula incidenta, iar al doilea termen este o unda plana regresiva, de amplitudine B, asociata cu particula reflecta in

In regiunea si ecuatia Schrödinger atemporala devine :

sau .

Deoarece putem nota (kappa) si ecuatia are solutia generala , care conduce la :

Din nou remarcam o unda plana progresiva pe care o asociem particulei transmise in si o unda plana regresiva care nu are sens fizic si pe care o eliminam :

In concluzie, functia de unda are expresia :

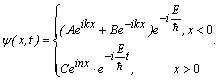
Punand conditia de continuitate a functiei de unda si a derivatei sale in obtinem :

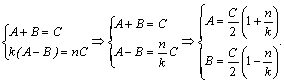
Coeficientul de reflexie al treptei de potential este definit de :

unde j este densitatea de curent de probabilitate :

Considerand obtinem :

Coeficientul de reflexie obtinut este: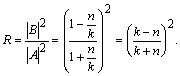

Coeficientul de torsiune: exprima probabilitatea ca o particula incidenta pe treapta de potential sa treaca dincolo de ea in regiunea Spre deosebire de particulele clasice, aceasta probabilitate este subunitara chiar in cazul .

In cazul in care particula soseste sa treapta de potential cu o energie mai mica decat inaltimea acesteia , ecuatia Schrödinger atemporala devine in regiunea sau cu solutia generala :

reala care nu mai corespunde unor unde.

Termenul trebuie eliminat pentru ca functia de unda al carei modul patrat exprima o probabilitate, sa ramana marginita cand Astfel obtinem:

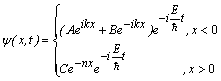
In coeficientul de torsiune: numaratorul se anuleaza, cantitatea ce trebuie introdusa in expresia lui fiind reala. Astfel coeficientul de referinta ca si in cazul clasic, dar exista o probabilitate proportionala cu care scade exponentul, de a gasi particula in regiunea