ELEMENTE DE CINEMATICA

ELEMENTE DE CINEMATICA

1. DEFINITII

A) CINEMATICA este partea mecanicii care studiaza miscarea corpurilor.

B) MISCAREA UNUI CORP reprezinta modificarea in timp a pozitiei sale in raport cu un sistem de referinta

C) TRAIECTORIA este locul geometric al pozitiilor succesive ale corpului aflat in miscare

2 MARIMI SPECIFICE CINEMATICII

LUNGIMEA drumului parcurs, poarta numele de spatiu ; U.M. in S.I. este metrul "m"

TIMPUL scurs intre momentul plecarii corpului si momentul opririi lui, reprezinta durata miscarii; U.M. in S.I. este secunda "s" .

3.TIPURI DE MISCARI

a- Miscarea de translatie

b- Miscarea de rotatie

c- Miscarea elicoidala

d- Miscare plan paralela

a.Miscarea de translatie

1. DEFINITII

u    Un corp efectueaza miscare de translatie, daca in cursul deplasarii, dreapta care uneste doua puncte arbitrare ale corpului ramane paralela cu ea insasi.

u    OBS: traiectoria corpului la miscarea de translatie rectilinie este o dreapta.

CLASIFICAREA MISCARILOR DE TRANSLATIE

I. In functie de sensul miscarii

a) miscare intr-un singur sens - miscare continua

b) miscare in ambele sensuri - miscare alternativa

II. In functie de modulul vectorului viteza in timpul miscarii

a) cu modul constant - miscare uniforma

b) cu modul variabil - miscare variata

3. STUDIUL MISCARII DE TRANSLATIE:

Notatii: consideram ca miscarea are loc pe directia axei Ox si notam cu:

x = coordonata mobilului la momentul t

x₀= coordonata mobilului la momentul t₀

t₀= momentul la care se incepe miscarea

v₀= viteza initiala (la momentul t₀)

v = viteza la momentul t

a = acceleratia

Miscarea rectilinie uniforma:

- legea deplasarii: x = x₀ + v∙ (t - t₀)

- legea vitezei: v = constant

- legea acceleratiei: a = 0

Miscarea rectilinie uniform variata ( = miscarea de translatie continuu variabila):

- legea deplasarii: x = x₀ + v₀∙(t - t₀) + [a∙ (t - t₀)²] / 2

- legea acceleratiei: a = constant

- legea vitezei: v = v₀ + a∙ (t - t₀)

- formula lui Galilei: v² = v₀² +2a∙Δx

RETINE: miscarea rectilinie uniform variata este de doua tipuri:

- uniform accelerata (a > o)

- uniform incatinita (a < 0)

Miscarea de translatie alternativa (ex: a unui piston in cilindru , este legata constructiv si functional de miscarea circulara a unui punt A) :

Ecuatiile pentru deplasare, viteza si acceleratie ale pistonului in miscarea de translatie alternativa, sunt cele specifica miscarii oscilatorii armonice.

Notatii:

A = punctul a carei miscare este urmarita

A^' = proiectia lui A pe diametrul vertical

Marimi caracteristice

- elongatia y = distanta de la A^' pana la centrul de oscilatie O:

y = A∙sinα = A∙sin ωt

- amplitudinea oscilatiei A = valoarea max. A elongatiei:

A =s / 2

S = 2R

- viteza in miscarea de translatie alternativa v:

v = v_c∙ cosα = ω∙ A∙cos ωt, unde v_c= viteza lui A pe traiectoria circulara (viteza tangentiala)

- acceleratia in miscarea de translatie alternativa a:

a = -a_n∙ sin ωt = - ω²∙ A∙sin ωt, unde semnul minus semnifica faptul ca in pozitia precizata de unghiul αvectorul acceleratie are sens invers vectorului viteza.

4.EXEMPLE DE MISCARI DE TRANSLATIE:

EXEMPLUL 1

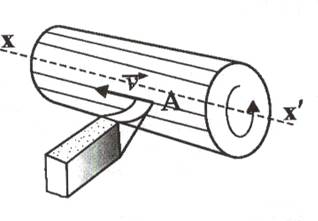
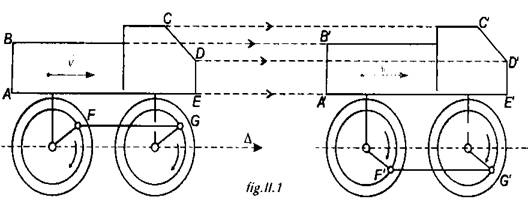
u    MISCAREA CREIONULUI LA TRASAREA UNEI LINII DREPTE

u    MISCAREA CUTITULUI DE STRUNG

u    MISCAREA UNUI MOBIL PE UN DRUM DREPT

EXEMPLUL 2

   

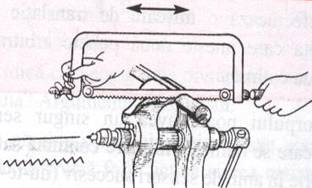
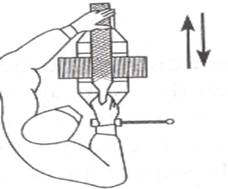
u    MISCAREA ACULUI DE LA MASINA DE CUSUT ELECTRICA

u    MISCAREA PISTONULUI DE LA MOTOARELE TERMICE

u    MISCAREA PILEI LA OPERATIA TEHNOLOGICA DE PILIRE

b.Miscarea de rotatie

1. DEFINITII

u    Un corp executa o miscare de rotatie daca fiecare punct al corpului se misca pe un cerc; centrele acestor cercuri se afla pe aceiasi dreapta numita axa de rotatie.

u    OBS. Corpul care in timpul miscarii sale are doua puncte care raman fixe, executa o miscare de rotatie

CLASIFICAREA MISCARILOR DE ROTATIE

I. In functie de sensul miscarii

a) miscare intr-un singur sens - miscare continua

b) miscare in ambele sensuri - miscare alternativa

II. In functie de modulul vectorului viteza in timpul miscarii

a) cu modul constant - miscare uniforma

b) cu modul variabil - miscare variata

3. STUDIUL MISCARII DE ROTATIE :

- Miscarea de rotatie continua uniforma(ω = constant) fig.1 - de desenat din manual pagina 26 fig II.7):

Notatii:

t = timpul ( se masoara in secunde s)

N = nr. de rotatii complete

Δθ = unghiul la centru parcurs de raza vectoare ( se masoara in radiani rad)

Marimile specifice intalnite la miscarea circulara se vor regasi si la miscarea de rotatie, respectiv:

- raza vectoare ( R) = vectorul de pozitie al mobilului, raza a cercului ce reprezinta traiectoria mobilului

- perioada miscarii (T) ( se masoara in secunde)= timpul necesar ca un punct al rigidului sa descrie o traiectorie circulara completa: T = t / N

- viteza unghiulara (ω) = variatia unghiului la centru α, in unitatea de timp ( se masoara in rad / s):

ω = Δθ / Δt

- frecventa de rotatie (υ) = nr. de rotatii efectuate in unitatea de timp ( se masoara in Hz - Hertzi):

υ = N / t

- viteza liniara (v) = raportul dintre variatia deplasarii, care este un arc de cerc Δs, si variatia timpului Δt ( viteza liniara se masoara in m / s): v = Δs / Δt

a_n = acceleratia normala ( numita si acceleratie centripeta sau acceleratie radiala fiind orientata catre centrul cercului traiectoriei); se masoara in m /s²

a_n = v² / R = ω∙ v = ω²∙ R =4∙ п² ∙R∙1 / T² == 4 ∙ п² ∙ υ² ∙ R

i_1,2 = raportul de trnsmitere intre doua roti 1 si 2 (fig.2 - de desenat din manual pagina 27 fig II.9):

i_1,2 = ω₁ / ω₂= (2 ∙ п ∙ υ₁) / (2 ∙ п ∙ υ₂) = n₁ / n₂

n = turatia exprimata in rotatii pe minut (rot / min)

υ = frecventa

Ecuatia de miscare: ∙ (t - t₀)

Relatii de legatura:

ω = Δθ / Δt = 2∙ п / T = 2∙ п ∙1 / T = 2 ∙ п ∙ υ

T

v = Δs / Δt = s / t = 2∙ п ∙R / T = 2∙ п ∙R ∙ 1 / T = 2 ∙ п ∙ υ ∙ R

v = ω∙ R = 2 ∙ п ∙ υ ∙ R

a = ω∙ υ= v²/ R = ω²∙ R= 4∙ п² ∙R∙1 / T² = 4 ∙ п² ∙ υ² ∙ R

RETINE: vectorul acceleratie este orientat spre centrul miscarii

- Miscarea de rotatie continua uniform variata (fig.3 - de desenat din manual pagina 29 fig II.15):

Legea m.r.c.u.v. : ∙t

= acceleratia unghiulara (se masoara in rad / s²)

= Δω/ Δt =(ω - ω₀) / (t - t₀)

θ = deplasarea unghiulara ( se masoara in rad)

θ= θ₀ + ω₀∙(t - t₀) + [ε∙ (t - t₀)²] / 2

v = variabil

a_t = acceleratia tangentiala ( situata permanent pe suportul vectorului viteza); se masoara in m /s²

a_t = Δv / Δt =(v - v₀) / (t - t₀)

v = v₀ + a_t ∙ t

s = lungimea totala a arcului de cerc descris in miscarea de rotatie uniforma

s= s₀ + v₀∙(t - t₀) + [a_t∙ (t - t₀)²] / 2

Relatii de legatura la m.r.c.u.v.

ε/ a_t = (ω/ t ) ∙(t / v) = ω / v

a_t =(v ∙ R∙ ω = R ε (se masoara in m / s)

ε = a_t / R ( se masoara in rad / s²)

4. EXEMPLE DE MISCARI DE ROTATIE

EXEMPLUL 1:

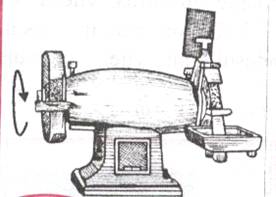
u    MISCAREA PIETREI DE POLIZOR

u    MISCAREA CHEII IN BROASCA

u    MISCAREA UNIVERSALULUI DE LA STRUNG

u    MISCAREA CREIONULUI LA TRASAREA UNUI CERC

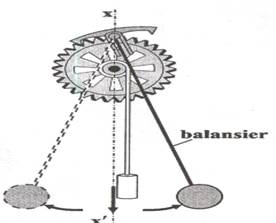
u    MISCAREA BALANSIERULUI DE LA PENDULA

u    MISCAREA ROTORULUI IN INTERIORUL STATORULUI

c.Miscarea elicoidala (fig.1 - de desenat din manual pagina 32 fig II.19):

1. DEFINITII

u    Un corp efectueaza o miscare elicoidala atunci cand proiectiile a doua puncte arbitrare ale sale, pe o dreapta fixa, se deplaseaza tot timpul miscarii.

u    OBSERVATII

1. Dreapta fixa pe care facem proiectia punctelor se numeste axa miscarii elicoidale
2. Miscarea elicoidala este compusa dintr-o miscare de rotatie si o miscare de translatie in directie paralela cu axa de rotatie
3. Curba care materializeaza traiectoria miscarii elicoidale se numeste elice.
4. Distanta dintre un punct oarecare al corpului si axa miscarii elicoidale este constanta.

STUDIUL MISCARII ELICOIDALE= miscarea compusa dintr-o rotatie si o translatie in directie paralela cu axa de rotatie; curba care materializeaza traiectoria miscarii elicoidale se numeste elice, de aici si denumirea acestui tip de miscare.

Cazuri particulare de miscari elicoidale

- miscarea de surub :in acest caz punctul va efectua doua miscari: una rectilinie uniforma cu viteza v₀, si alta de rotatie uniforma ce produce viteza tangentiala v_t; cele doua viteze componente fac un unghi de 90s, si dau viteza rezultanta v, al carei modul este:

v² = v₀² + v_t² = v₀² + ∙ R²

ω = constant, deci in cazul miscarii de surub exista o singura acceleratie, cea centripeta

3. EXEMPLE DE MISCARI ELEICOIDALE

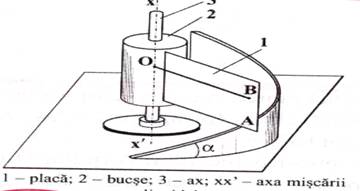
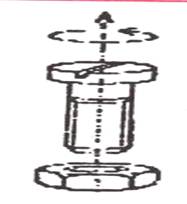
u    Miscarea tarodului respectiv a filierei la filetarea manuala

u    Miscarea burghiului la operatia de gaurire

u    Miscarea glontului pe teava

u    Miscarea realizata de robinet la deschidere/inchidere

u    Miscarea surubului/piulitei la insurubare/desurubare

d. Miscarea plan paralela (fig.1 si fig.2- de desenat cele prezentate in material inclusiv cel din exemple- mecanismul biela- manivela):

1. DEFINITIE

u    Un corp efectueaza miscare plan-paralela, atunci cand trei puncte ale sale, necoliniare, raman in tot timpul miscarii intr-un plan fix, numit plan director.

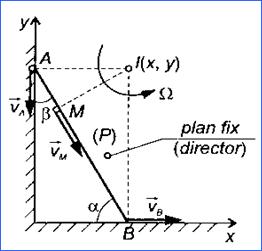
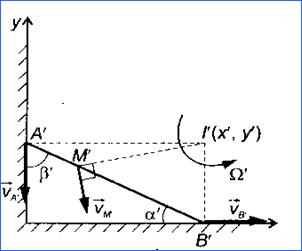
OBSERVATII:

u    1. In planul fix exista un punct a carui viteza este nula si poarta numele de centru instantaneu de rotatie

u    Punctele corpului care au viteza zero se gasesc pe o dreapta perpendiculara pe planul fix al miscarii, numita axa instantanee de rotatie

u    3. Pozitia axei instantanee de rotatie si a centrului instantaneu de rotatie se schimba mereu, de aceea corpul nu executa miscare de rotatie in jurul axei instantanee de rotatie

3. EXEMPLE DE MISCARI PLAN - PARALELE:

u    Mecanismul pantograf

u    Alunecarea unei scanduri pe dusumea scandura fiind sprijinita de perete

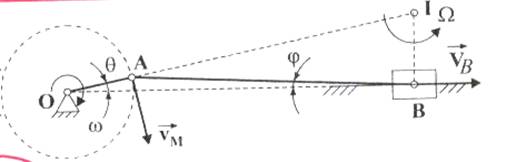
u    Mecanismul biela manivela