PROPRIETATI OPTICE, MECANICE,

TERMICE SI CHIMICE ALE MATERIALELOR OPTICE

1. Generalitati

Lumina sau radiatia electromagnetica, in general, incidenta pe suprafata unei structuri materiale interactioneaza cu aceasta. Principalele fenomene optice prin care se manifesta aceasta interactiune sunt transmisia, reflexia si absorbtia. Masura in care aceste fenomene se manifesta depinde de natura materialului si are determinare spectrala in ceea ce priveste radiatia.

Radiatia electromagnetica este descrisa prin ecuatiile lui Maxwell, intr-o formulare care implica marimi caracteristice campurilor electric si magnetic, definite prin legile lui Faraday, Gauss si Ampere si care demonstreaza faptul ca, intr-un mediu omogen si izotrop, lumina este o unda transversala, caracterizata printr-un vector electric si unul magnetic, cu interactiune permanenta reciproca. Vectorii intensitate electrica si intensitate magnetica oscileaza in plane perpendiculare intre ele si perpendiculare pe directia de propagare a undei , astfel incat vectorii formeaza un triedru drept.

Proprietatile optice ale radiatiei electromagnetice, respectiv procesele care se manifesta la interactiunea radiatie-materie sau radiatie-radiatie (transmisie, reflexie, absorbtie, difuzie, interferenta, difractie, polarizare) sunt determinate de caracteristicile vectorului intensitate electrica si frecventa de oscilatie.

O unda electromagnetica plana, monocromatica, propagata printr-un mediu omogen si izotrop, este descrisa prin ecuatia:

, (1.1)

unde reprezinta vectorul intensitate electrica a campului electric asociat undei,

- vectorul amplitudine al intensitatii electrice in vid

- numarul de unda (marime vectoriala care are directia si sensul directiei de propagare a undei si modulul: , cu w - pulsatia undei, v - viteza de propagare, n - frecventa)

- vectorul de pozitie spatiala a undei

t - timpul.

O ecuatie formal identica relatiei (1.1) poate fi scrisa si pentru vectorul oscilant intensitate magnetica, pentru a caracteriza campul magnetic asociat undei.

Aplicand ecuatiile lui Maxwell, campul electric al unei unde electromagnetice care se propaga intr-un mediu liniar, omogen si izotrop, verifica ecuatia:

, (1.2)

unde m este permitivitatea magnetica a mediului (m m_om_r, m_o=permitivitatea magnetica a vidului, m_o p.10^-7 H/m, m_r=permitivitatea relativa a mediului) , s - conductivitatea mediului (s=0 pentru dielectrici), e - permitivitatea electrica a mediului (e e_oe_r e_o= permitivitatea electrica a vidului, e_o=8.854187187.10^-12 F/m).

Conditia (1.2) pentru expresii ale vectorului intensitate electrica a campului de forma (1.1) conduce la solutii de forma:

, (1.3)

unde: .

Marimea cu simbolul reprezinta indicele de refractie complex, a carei parte reala n este indicele de refractie real. In partea imaginara a expresiei indicelui de refractie complex, marimea c se numeste coeficient de amortizare sau atenuare.

Vectorul de unda in vid k_o are forma:

, unde c este viteza luminii in vid: (1.4)

. (1.5)

Simbolurile e' si e" constituie partea reala, respectiv imaginara a permeabilitatii electrice totale a mediului si conform relatiei (1.3), aceste marimi se pot exprima functie de indicele de refractie real si coeficientul de amortizare sub forma:

, (1.6)

. (1.7)

Intr-un mediu diferit de vid, indicele de refractie si coeficientul de amortizare se definesc functie de permeabilitatea electrica, dupa urmatoarele legi:

, (1.8)

. (1.9)

Viteza luminii in mediul cu indice de refractie real n este:

. (1.10)

Ca o concluzie se poate afirma ca viteza de propagare si valorile marimilor caracteristice ale campului electric purtat de radiatia electromagnetica depind si sunt influentate de proprietatile mediului in care are loc propagarea.

Reciproc, proprietatile optice ale mediilor pe care este incidenta radiatia electromagnetica vor reprezenta efecte ale interactiunii campurilor electrice proprii cu campul electric oscilant asociat radiatiei.

Avand in vedere faptul ca in constructia aparatelor optice formarea imaginilor se bazeaza pe refractie sau reflexie, se urmareste utilizarea unor materiale cu transparenta (sau tramsnitanta), respectiv reflectanta cat mai ridicate. Din punct de vedere energetic (fotometric sau radiometric) pierderile prin absorbtie trebuie sa fie cat mai mici.

La nivel de structura atomica a substantei caracterul de transparent, opac sau reflectant este determinat de masura in care radiatia electromagnetica incidenta stimuleaza trei procese fizice de baza: tranzitii electronice in banda de valenta, vibratii ale retelei cristaline si efecte ale purtatorilor liberi. Procesul dominant depinde de natura materialului si de caracteristica spectrala a radiatiei. Absorbtia este, in principal, determinata de tranzitiile electronice (In principiu, saltul electronului de valenta pe nivelul energetic superior are loc prin absobtia unei cuante de energie luminoasa, care corespunde unei anumite frecvente spectrale. Cantitatea de energie absorbita de substanta este proportionala cu concentratia speciei atomice sensibile la frecventa respectiva, astfel incat radianta spectrala in fasciculul emergent va fi mai mica decat in cel incident, ceea ce din punct de vedere optic defineste o scadere a transmitantei spectrale.). Totusi, transparenta (in special a semiconductorilor in infrarosu) este afectata si de absorbtia datorata vibratiilor la nivelul retelei cristaline (Frecventele din domeniul infrarosu stimuleaza tranzitii de vibratie ale moleculelor, scazand radianta spectrala emergenta, respectiv transmitanta). Efectul purtatorilor liberi este important pentru semiconductori si metale ale caror proprietati optice privind transmisia si absorbtia depind mai ales de acest efect.

La un nivel mai profund de subtilitate, transparenta unui material optic este influentata si de prezenta impuritatilor care induc efecte locale de absorbtie, ca si procesele multifoton care cauzeaza pierderi energetice radiante in cazul metalelor expuse unor fascicule in domeniul infrarosu.

Transparenta - cu precadere in domeniul vizibil - ,ca proprietate de prima importanta pentru functionarea lentilelor, prismelor, reticulelor etc. impune alegerea unor materiale dielectrice pentru executia pieselor. Semiconductoarele pot fi utilizate ca medii refractante numai in domeniul infrarosu.

Transparenta este strict legata de pozitia benzii interzise pe o scara a energiei (fig.1.1.).

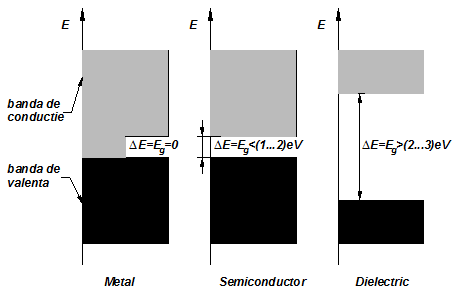
Fig.1.1. Pozitia si marimea benzii interzise la metale, semiconductoare

si dielectrice (izolatoare)

Radiatia nu este absorbita de material in masura in care frecventa sa ii asigura o energie care se incadreaza in banda interzisa a materialului, astfel incat absorbtia la nivel electronic, de vibratie sau prin efect al purtatorilor liberi sa nu aiba loc, iar radianta spectrala sa se conserve intr-o mare masura.

Pentru frecvente mai mici decat cele care determina energii din banda interzisa, materialul este - total sau partial, integral sau selectiv din punct de vedere spectral - absorbant, functie de caracteristicile concrete ale atomilor si retelei de dispunere a acestora. La frecvente corespunzatoare benzii de conductie, materialele dielectrice sunt preponderent reflectante.

Metalele, in domeniul optic (UV-VIS-IR) sunt opace si pot prezenta reflectanta spectrala selectiva in anumite conditii de finisare a suprafetei de incidenta. La metale, benzile de valenta si conductie sunt alaturate sau partial suprapuse, neexistand banda interzisa. Aceasta are o extindere relativ ingusta la materialele semiconductoare, care pot fi transparente pe domenii relativ restranse.

Ca materiale optice transparente, pentru constructia componentelor bazate pe refractie se utilizeaza, deci, dielectricii si semiconductoarele (pentru zona IR), iar ca materiale reflectante - metalele.

Avand in vedere popularea statistic-probabilistica a nivelurilor energetice ale structurilor materiale, prezenta aleatoare ca natura si distributie a unor impuritati, precum si o directa determinare spectrala, rezulta ca materialele optice nu vor avea niciodata coeficienti radiometrici ideal unitari, ci valori medii mai mult sau mai putin apropiate de cele ideale, functie de structura concreta a materialului, de compozitia spectrala si intensitatea radiatiei cu care interactioneaza.

2. Materiale optice

Materialele utilizate ca medii optice se pot incadra in trei mari categorii: sticle minerale amorfe, mono sau policristale si sticle organice.

Sticlele optice minerale amorfe sunt utilizate datorita transmitantei ridicate in VIS, omogenitatii, turnarii usoare si prelucrarii la costuri relativ reduse, precum si potentialei disponibilitati la orice indice de refractie intr-o gama data. Tehnologia de obtinere a semifabricatului sub forma unui bloc, presupune realizarea unui amestec omogen, in stare topita, a compozitiei specifice sortului de sticla si racirea lenta, pentru solidificarea fara cristalizare.

Sticlele amorfe, care nu prezinta nici un fel de simetrie structurala, sunt considerate, teoretic, izotrope. In acest sens, proprietatile materialului optic depind de viteza de racire si distributia vitezei de racire in masa semifabricatului. Temperaturile neuniforme conduc la variatii locale de densitate, care induc tensiuni remanente ca surse de anizotropie.

Indicii de refractie, caracteristicile de dispersie, proprietatile termice si mecanice diferite rezulta prin adaugarea in proportii controlate de oxizi de litiu, bariu, bor, fosfor, plumb etc. unei mase de baza constituite din bioxid de siliciu (SiO₂).

De exemplu, oxidul de bariu (BaO) determina obtinerea unor indici de refractie mari si coeficienti de dispersie mici, in timp ce un oxid al borului (B₂O₃) - indice mic si dispersie foarte redusa. Indicii foarte mici si dispersii foarte reduse rezulta prin adaosuri de floruri in locul oxizilor. Pentru indici foarte mari la dispersii relativ mici este specific adaosul de pamanturi rare, cu precadere lanthanul. Alti oxizi, cum ar fi ai aluminiului si metalelor alcaline contribuie la stabilitatea chimica, rezistenta la umezeala a sticlelor.

Extinderea domeniului spectral in zona ultravioleta a fost posibila prin introducerea in masa de baza a flor-fosfatilor si florurilor. Sticlele fara oxizi cu adaosuri de sufura de arseniu (As₂S₃) si floruri ale metalelor grele cum ar fi florura de zirconiu (ZrF₄) sunt utilizate pentru infrarosul mediu si indepartat.

Sorturile de sticla optica se identifica printr-o simbolizare alfanumerica. In simbol este inclus un grup de litere reprezentand sortul sticlei urmat de un numar format din sase cifre. Primele trei cifre corespund primelor trei zecimale ale indicelui de refractie, iar urmatoarele trei numarului Abbe inmultit cu 10.

Densitatea sticlelor minerale variaza intre (2.4 . 5.4)g/cm³, functie de cantitatea si densitatea elementelor de adaos.

In tabelul 1.1 sunt prezentate cateva sorturi reprezentative de sticle minerale si caracteristicile lor.Tabelul 1.1.

Tabelul 1.1

* sorturi din productia altor firme decat Schott

Transmitanta sticlei optice are valori ridicate intr-o regiune larga a spectrului electromagnetic, ceea ce o recomanda ca material utilizabil pentru domeniile ultraviolet apropiat, vizibil si infrarosu apropiat (l=350nm . 2.5mm).

Cristalele mono sau policristaline, naturale sau artificiale pot fi utilizate pe scara larga pentru executia componentelor optice. Monocristalele rezulta prin cresterea din topitura a unui cristal prin diverse tehnologii. Policristalele se obtin prin sinterizare sau depunere de vapori, rezultand conglomerate de microcristale (cca. 50 micrometri), avand orientari aleatoare si frontiere bine delimitate prin lipsa de continuitate a retelelor cristaline. Policristalele sunt mai rezistente mecanic, mai dure, dar introduc pierderi prin difuzie mai mari decat monocristalele. Industria cristalelor optice s-a dezvoltat ca urmare a aplicatiilor tot mai numeroase in domeniul UV si, mai ales, IR, in care sticla optica traditionala are transmitanta scazuta sau este absorbanta, functie de sort.

In tabelul 1.2 sunt prezentate cateva tipuri de cristale optice si principalele lor caracteristici optice.

Tabelul 1.2

Sticla organica este un material optic neconventional, inclus in constructia aparatelor optice doar in ultimii ani. Avantajele maselor plastice, dintre care primeaza densitatea redusa - (0.7 . 1.3) g/cm³ - si tehnologia ieftina de obtinere a piesei optice finite (o singura operatie de turnare sau matritare, fara finisare ulterioara), au determinat o extindere rapida a utilizarii sticlelor organice.

Cateva dintre cele mai importante mase plastice utilizate ca materiale optice sunt prezentate in tabelul 1.3.

Tabelul 1.3

Sticlele organice au indici de refractie mai mici (n_d=1.4 . 1.7) decat sticla minerala si un domeniu spectral de lucru limitat la visibil (in UV si IR polimerii bazati pe carbon sunt puternic absorbanti).

Un avantaj al sticlelor organice este faptul ca pot fi colorate, practic in orice culoare, fie prin depunerea stratului filtrant spectral pe suprafata lentilei, fie prin colorarea in masa.

Rezistenta scazuta la actiunea factorilor mecanici nu mai reprezinta un dezavantaj datorita tratamentelor de durificare superficiala care s-au dezvoltat si care aduc proprietatile mecanice ale componentelor din plastic la nivelul celor din sticla.

Totusi, din punct de vedere optic, cea mai importanta caracteristica este uniformitatea indicelui de refractie in masa materialului. O ierarhizare pe acest criteriu claseaza pe primul loc monocristalele, urmate de sticlele amorfe, policristale si apoi sticlele organice.

3. Proprietatile materialelor optice

Proprietatile materialelor optice pot fi analizate din punct de vedere optic, mecanic, termic, electric etc. Cele mai importante, care impun alegerea materialului, sunt cele optice.

3.1.Proprietatile optice ale materialelor optice

Caracteristicile mediilor optice se raporteaza la fenomenele de refractie, transmisie, dispersie, reflexie si absorbtie a luminii.

a) Refractia unui sort de sticla optica este definita prin indicele de refractie, n, al sticlei, in raport cu aerul. Intrucat indicele de refractie este variabil cu lungimea de unda l a radiatiei luminoase, in cataloagele firmelor producatoare de sticla optica se precizeaza valoarea acestuia pentru diferite lungimi de unda. In cataloagele recente, acesti indici sunt specificati pentru lungimile de unda ale mai multor linii spectrale ale unor elemente chimice (23 sunt mai frecvent folosite) si pentru 12 lungimi de unda generate de cei mai utilizati laseri. Cataloagele pe suport electronic, permit determinarea indicelui de refractie pentru orice lungime de unda prin indicarea, la fiecare sort de sticla, a polinomului de interpolare pentru functia indice de refractie, avand ca variabila independenta lungimea de unda.

Indicele de refractie n_e corespunzator lungimii de unda l_e=546.07nm, din spectrul mercurului este cunoscut ca indice de refractie de referinta (principal), intrucat aceasta linie spectrala se afla cel mai aproape de radiatia avand l = 555 nm, pentru care ochiul uman prezinta sensibilitatea maxima. Linia de referinta e a fost impusa in Europa de cel mai mare si prestigios producator de sticla optica, firma Schott. In Statele Unite se lucreaza si cu linia d ca referinta spectrala.

Prima determinare analitica a dependentei indicelui de refractie de lungimea de unda a fost realizata de Sellmeier (si independent de Maxwell) si avea in vedere influenta absorbtiei electronice si a vibratiilor din nodurile retelei cristaline. Diverse aproximari sau completari aduse formulei initiale au condus la imbogatirea literaturii cu mai multe expresii de polinoame de interpolare, dupa cum urmeaza:

Cauchy (3.1)

Hartmann (3.2)

Conrady (3.3)

Kettler-Drude (3.4)

Sellmeier (3.5)

Herzberger (3.6)

Old Schott . (3.7)

Catalogul Schott nou utilizeaza ecuatia Sellmeier (3.5) si precizeaza valorile numerice ale coeficientilor a . g pentru toate sorturile de sticla din catalog. Relatia (3.7) utilizata de firma Schott pentru datele prezentate in cataloagele mai vechi introducea o eroare de ordinul 3.10^-6 in vizibil si 5.10^-6 in UV si IR. Expresia putea fi corectata prin introducerea unui termen in l pentru UV si in l pentru IR. Introducerea in fabricatie a sorturilor de sticla noi, cu transmitanta ridicata pe domenii spectrale largi, care se extind mult in afara vizibilulului a impus reconsiderarea alegerii polinomului de interpolare in scopul rigurozitatii determinarii indicelui de refractie si pentru utilizarea corecta, la parametrii potentiali ai materialului optoc respectiv.

Binoamele de la numitorii din polinoamele de interpolare evidentiaza prin constantele specifice liniile de absorbtie caracteristice fiecarui sort de sticla. Formularea Cauchy si Old Schott plaseaza benzile de absorbtie la lungimi de unda nule, neglijandu-le de fapt.

Formula Herzberger aproximeaza corect pana la aproximativ 1mm si in ultimele sale lucrari a inlocuit linia 0.035 cu 0.026.

Aparitia sticlelor minerale performante, cu acoperire spectrala larga a impus una dintre interpolarile Sellmeier (rel.3.5).

b) Dispersia luminii reprezinta fenomenul de dependenta a indicelui de refractie al sticlei optice de lungimea de unda a radiatiei luminoase si matematic se exprima prin raportul dn/dl

Reprezentarea grafica a dependentei n=n(l) defineste curba de dispersie a mediului optic respectiv.

In figura 3.1 este prezentata, spre exemplificare, curba de dispersie pentru sticla TF5 in domeniul vizibil.

Dispersia materialelor optice in domeniul vizibil este monoton descrescatoare (dispersie normala) dar neliniara de la albastru spre rosu si nu poate fi caracterizata printr-un singur parametru. In afara vizibilului dispersia este anormala, curba prezentand extreme locale, corespunzatoare absorbtiei unor linii sau benzi spectrale.

Caracterul neliniar al dispersiei face imposibila descrierea proprietatilor dispersive ale materialului printr-un singur parametru numeric.

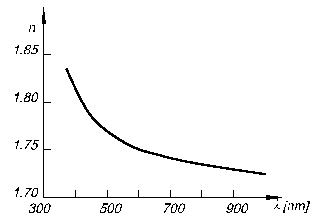
Fig.3.1. Curba de dispersie a sticlei TF5

Se definste urmatorul set de parametri dispersivi:

- dispersia principala (medie):

, (3.8)

unde F' si C' simbolizeaza liniile albastra, respectiv rosie care delimiteaza partea cea mai mare a energiei din spectrul vizibil.

- dispersii partiale:

, (3.9)

cum sunt n_G'-n_g, n_D- n_d, n_g-n_h, n_F-n_g, n_e-n_F, n_C-n_e, n_A'-n_C etc;

- refringenta optica:

sau ; (3.10)

- coeficientii de dispersie Abbe:

sau ; (3.11)

Numarul lui Abbe se inscrie in intervalul n_e=(16.5 . 105), majoritatea valorilor incadrandu-se in domeniul (40 . 70). Valori mult mai mari ale coeficientului Abbe pot avea unele cristale destinate utilizarii in IR (n

- dispersia partiala relativa:

, (3.12)

care este definita in cataloage pentru mai multe zone spectrale.

Dispersiile partiale relative q_g,F si q_C,s

(3.13)

sunt de interes la corectarea aberatiilor cromatice in spectrele secundare.

- dispersia specifica:

n_H - n_C (3.14)

- puterea dispersiva, reprezentand inversul coeficientului de dispersie:

, (3.15)

c) Transmitanta sticlei optice are o valoare mare in domeniul (450 . 1000) nm. Pentru lungimi de unda mai mici de 450 nm , sorturile cu indici de refractie mari prezinta valori superioare ale coeficientului de absorbtie.

Pentru a putea caracteriza transmitanta, firmele mentioneaza in cataloage valori ale coeficientilor radiometrici spectrali, determinati pentru probe de sticla prelucrate sub forma de lame plan-paralele, avand grosimi precizate in cataloage.

Atenuarea fluxului luminos incident, F_i, se datoreaza pierderilor la trecerea prin mediul optic. Acestea sunt de doua categorii: prin reflexie la suprafetele de separatie a materialului optic dens cu aerul si prin absorbtie in masa materialului (fig.3.2).

Astfel, considerand o piesa de forma unei lamele plan paralele, pe care este incident fluxul F_i, in interiorul piesei, efectiv, patrunde fluxul F_in < F_i, datorita reflexiei pe prima fata. Pe a doua fata ajunge fluxul F_ex < F_in, diminuarea fiind cauzata de absorbtia pe parcursul d. Din fata a doua a piesei emerge F_t < F_ex, pierderea fiind determinata de reflexia pe suprafata 2 a lamei.

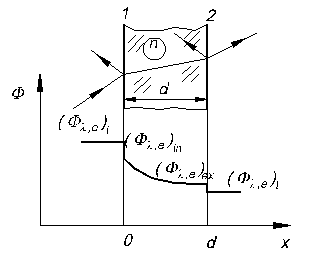
Fig.3.2. Pierderi de lumina prin mediile optice dense

Intre valorile fluxurilor energetice sau luminoase de la incidenta pe prima fata pana la emergenta din a doua suprafata, se pot scrie relatii care definesc coeficientii radiometrici (sau fotometrici). In forma cea mai cuprinzatoare, care are in vedere si determinarea spectrala a reflexiei, absorbtiei si transmisiei, acestia au urmatoarele expresii:

- coeficientul spectral de transmisie externa:

, (3.16)

unde (F_e,l)_t este fluxul radiant transmis de proba, iar (F_e,l)_i reprezinta fluxul radiant incident;

- coeficientul spectral de reflexie:

, (3.17)

unde (F_e,l)_r este fluxul radiant reflectat de proba;

- coeficientul spectral de absorbtie:

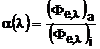, (3.18)

unde (F_e,l)_a este fluxul radiant absorbit de proba;

-coeficientul spectral de transmisie interna:

(3.19)

unde (F_e,l)_ex este fluxul radiant incident pe a doua fata a lamelei, iar (F_e,l)_in reprezinta fluxul radiant care intra in proba dupa pierderea prin reflexie pe prima fata a acesteia;

- coeficientul spectral de absorbtie interna:

, (3.20)

Intre acesti coeficienti exista relatiile:

t_ext l r l a l (3.21)

t_int l a_int l (3.22)

t_int l) = . (3.23)

Se observa ca:

a_int l)> a_ext l (3.24)

t_int l) > t_ext l (3.25)

Cu aceste consideratii privind pierderile prin absorbtie in masa materialului piesei optice si prin reflexii pe cele doua fete, fluxul transmis va fi :

, (3.26)

sau:

, (3.27)

unde r este reflectanta unei suprafete.

Pentru sticla optica fara protectie antireflex, r 0,04 si a_i 0,002 si rezulta un factor de transmisie externa curent t_ext 0,92, la grosimea de 1mm, in lumina alba.

3.2. Proprietati termice ale sticlei optice

Temperatura are o influenta hotaratoare asupra caracteristicilor optice ale sticlei, fiind un factor determinant al tehnologiei de fabricatie si al stabilitatii constantelor optice in exploatare.

Domeniul de temperaturi la care se formeaza sticla este cuprins, pentru majoritatea sorturilor, intre 400^oC si 600^oC.

Viteza de racire de la 600^oC la temperatura camerei trebuie aleasa adecvat pentru a se asigura o tranzitie lenta de la faza lichida la faza solida. Viteza lenta de racire asigura valori scazute ale tensiunilor interne (pentru evitarea pericolului spargerii sticlei sau al manifestarii fenomenului de birefringenta) si o fixare a moleculelor intr-o retea densa (conditie a obtinerii unui indice de refractie ridicat).

Indicele de refractie variaza cu temperatura atat datorita dilatarii sau contractiei termice, cat si deplasarii limitei de absorbtie din domeniul UV al spectrului catre domeniul VIS. Pentru sticlele crown este mai semnificativa contactia/dialtatia care determina cresterea/scaderea indicelui de refractie decat deplasarea limitei de absorbtie, care se afla in UV indepartat. La sticlele flint este mai importanta in special cresterea temperaturii, datorita faptului ca au limita de absorbtie aproape de domeniul VIS.

Datorita deplasarii benzii de absorbtie spre lungimi de unda mai mari majoritatea sortuirlor de sticla prezinta in timp coloratii diferite (la inceput galben, apoi portocaliu si, in final rosu).

Din punct de vedere termic, sticlele optice se caracterizeaza prin urmatorii parametri:

- temperatura de curgere - temperatura la care sticla devine un fluid vascos

- temperatura de formare - temperatura la care tensiunile interne din sticla se elimina in cca. 15 minute

- temperatura de tragere - temperatura la care sticla poate fi deformata

- temperatura de patrundere - temperatura la care sticla patrunde in porii unei placi pe care este asezata

- temperatura de lucru - temperatura de prelucrare a pieselor optice.

Se defineste coeficientul de dilatare termica liniara ca alungirea unitatii de lungime a unui esantion de sticla incalzit cu 1^oC. Coeficientul de dilatare termica este dependent de temperatura. Din acest motiv cataloagele dau valori medii ale coeficientului de dilatare pentru doua domenii de temperatura (de la - 60^oC la 20^oC si de la 20^oC la 120^oC).

Pentru a stabili o valoare aproximativa a coeficientului de dilatare in intervalul de temperaturi [20^oC . 400^oC] se poate utiliza expresia de interpolare:

,

unde a este coeficientul de dilatare termica la 20^oC (data de catalog)

m - coeficient de temperatura (data de catalog)

t - temperatura limita a intervalului pentru care se calculeaza coeficientul de dilatare.

Valoarea a_20/t se incadreaza intre limitele (33 . 136).10^{-7 o}C^-1 ,dar pentru majoritatea sorturilor se grupeaza in intervalul (50 . 90).10^{-7 o}C^-1 (valorile mai ridicate corespund sorturilor cu continut mai bogat in metale alcaline). Aceasta marime prezinta interes deosebit atunci cand un aparat lucreaza la variatii mari de temperatura, precum si in cazul lipirii componentelor optice. Pentru lipire se admite o variatie a coeficientilor de dilatare Da=7.10^{-7 o}C^-1.

Conductivitatea termica l_t reprezinta capacitatea sticlei de a conduce caldura si se defineste prin cantitatea de caldura (exprimata in kcal sau J) care traverseaza o suprafata de 1mp pe unitatea de timp (ora sau secunda), la un gradient de temperatura care initiaza transferul termic egal cu 1^o/m.

Conductivitatea termica depinde de temperatura. Cataloagele contin valori de referinta ale parametrului pentru patru temperaturi: - 50^oC, 0^oC,20^oC, 50^oC.

La temperatura standard, conductivitatea termica este de ordinul l =(0.5348 . 1.1045)J/ms^oC, majoritatea valorilor fiind grupate in intervalul (0.58 . 0.93) J/ms^oC.

Caldura specifica a sticlelor optice este cvasiconstanta pentru majoritatea sorturilor si are valoarea c=920 J/kgK.

3.3. Proprietati mecanice ale sticlei optice

Cunoasterea proprietatilor mecanice ale sticlei este importanta atat in procesul de prelucrare cat si pentru montarea componentelor optice.

Masa specifica, r, este indicata in cataloage pentru conditii standard si are valori in intervalul (2.27 . 6.97) g/cmc. Acest parametru depinde nu numai de compozitia chimica ci si de temperatura de formare a semifabricatului.

Modulul de elasticitate, E, caracterizeaza proprietatile elastice ale sticlei. Relatia de dependenta intre modulul de elasticiate longitudinal, E, modulul de elasticitate transversal, G si coeficientul Poisson este de forma:

.

Pentru majoritatea sticlelor optice E are valori in intervalul (5.4 . 8.34).10⁴ N/mm².

Se defineste duritatea la slefuire, HS si duritatea la zgariere masurata in unitati Martens (32.5 . 80.5).

Coeficientul tensiunii optice reprezinta un factor de proportionalitate intre tensiunile pe directiile diferite determinate de birefringenta si diferenta indicilor de refractie pe aceste directii:

,

Dn este diferenta indicilor de refractie pe doua directii 1 si 2

d - diferenta de drum optic, in nm, care apare la trecerea luminii polarizate printr-un esantion tensionat

B - coeficientul optic al tensiunii materialului

s - tensiunile normale corespunzatoare directiilor 1 si 2

s - grosimea esantionului.

Coeficientul optic al tensiunii este indicat in cataloage pentru lungimea de unda de 550nm in conditii standard. B are valori uzuale in domeniul (0.58 . 3.90)(nm/cm)/(daN/cm²).

Unele sortuir de sticla, cum ar fi STF3 si STF11 au valori B negative ( -1.35, respectiv - 2.30).

Coeficientul B are valoarea unitara atunci cand o tensiune de 1daN/cm² determina o birefringenta de 1nm/cm.

Vascozitatea este definita ca raport dintre tensiunea de forfecare din sticla in stare fluida si gradientul de viteza normal pe directia de curgere a acesteia. Vascozitatea sticlelor optice, masurata in Poise, este de 10^7.6 la temperatura de inmuiere, de 10¹³ la temperatura de formare si de 10^14.5 la temperatura de deformare.

3.4. Proprietatile electrice ale sticlei optice

La temperatura camerei, sticla are o rezistivitate electrica foarte ridicata (10¹⁴ . 10¹⁶)Wm.

La temperaturi ridicate conductivitatea elctrica poate fi ridicata, functie de sort, datorita mobilitatii ionilor in special alcalini (la peste 1400^oC rezistivitatea scade la cca. 10³ Wm.

4. Aprecierea calitatii sticlei optice

Alegerea adecvata a sortului de sticla optica si a calitatii acesteia in acord cu cerintele functionale impuse fiecarei componente optice reprezinta o preocupare de baza a proiectantilor de aparate optice.

Calitatea sticlei optice este apreciata pe baza unor parametri standardizati ale caror valori definesc categorii sau clase de calitate. Aceasta este controlata prin urmatorii parametri:

- abaterea admisa la indicele de refractie de referinta, Dn_e (sau Dn_d) si dispersia medie, D(n_F'-n_C') (sau D(n_F-n_C)). Proiectantul prescrie categoria sau direct valoarea parametrilor, conform tabelului 4.1. Variatiile mari ale caracteristicilor optice ale sticlei conduc la cresterea aberatiilor geometrice, respectiv cromatice si diminueaza calitatea imaginii.

Tabelul 4.1

omogenitatea (definita pe cinci categorii, conform tabelului 4.2). Omogenitatea optica se apreciaza prin raportul j j_o, dintre unghiul teoretic de separare al aparatului de control si unghiul limita de separare prin semifabricatul de sticla.

Tabelul 4.2

birefringenta (apreciata prin sase categorii, asa cum rezulta din tabelul 4.3). Se masoara ca diferenta de drum intre raza ordinara si extraordinara pe 1 cm de parcurs prin sticla.

Tabelul 4.3

absorbtia (apreciata prin sapte categorii, conform tabelului 4.4), prin coeficientul de absorbtie a

Tabelul 4.4

striurile (sau incluziunile filiforme), care au diametrul de ordinul zecimilor de milimetru si se incadreaza in doua clase dupa cum examinarea semifabricatului se face dupa doua directii perpendiculare (clasa A) sau dupa o singura directie (clasa B).

bulele (impatite in 11 categorii si sase clase, detaliate in tabelele 4.5 si 4.6).

Tabelul 4.5

Tabelul 4.6

Defectele de material se admit la valorile prevazute in categoriile medii pentru componente care nu se afla intr-un plan imagine. Pentru piese aflate intr-un plan imagine (reticule, scari gradate) prezenta bulelor si a striurilor nu este permisa.

5. Caracteristici si incercari specifice sticlelor optice. Catalogul Schott 2005

5.1. Catalogul de sticle optice Schott

Firma Schott reprezinta cel mai prestigios producator de sticla optica european.

Catalogul Schott 2005 este prezentat in anexa sub forma unui document Excel, care ofera 118 sorturi de sticle optice, avand proprietati optice, mecanice si termice variate

In forma grafica, sorturile de sticla se reprezinta prin puncte intr-un sistem de axe n-n (Diagrama Abbe). In aceasta reprezentare se pot pun in evidenta familiile de sorturi bazate pe o anumita compozitie chimica (K, F, BK, FK, LaK, PSK, SK, BaSF etc.).

In figura 5.1 este redata pozitia sticlelor Schott in diagrama n-n, realizata pe baza datelor din catalog.

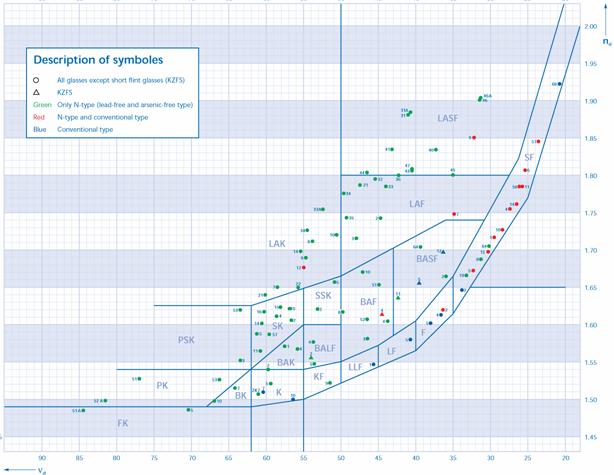
Sunt descrise in continuare semnificatia valorilor inscrise in coloanele catalogului, precum si metodele de masurare a caracteristicilor sticlelor, asa cum sunt prevazute de standardele europene si aplicate de catre producator.

5.2. Simbolizarea sticlelor optice

Sticlele optice sunt simbolizate prin coduri alfanumerice care au la baza in principal continutul chimic al sortului si respectarea clasificarii traditionale in familiile de sticle crown (K) si flint (F). Denumirea sortului nu contine valori ale caracteristicilor optice sau termo-mecanice. De aceea fiecarui sort ii este asociat un cod, care contine informatii privind cele mai importante caracteristici ale sticlei.

Codificarea sorturilor de sticle optice presupune un sir de 9 caractere format din doua grupuri de 6, respectiv 3 cifre separate prin punct. Primele trei cifre indica primele trei zecimale ale indicelui de refractie de referinta n_d, umatoarele trei valoarea rotunjita in sus a numarului Abbe multiplicat cu 10, iar ultimul grup de trei cifre exprima densitatea in g/cmc multiplicata cu 100.

In figura 5.2 este exemplificat modul de codificare al sorturilor N-SF6 si SF6.

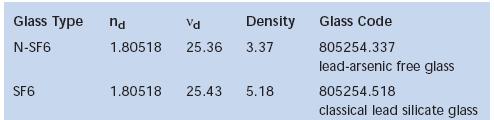
Fig. 5.2. Exemplu de codificare a sorturilor de sticle optice

In catalogul Schott fiecare sort are asociat un cod inscris in coloana FC.

5.3. Proprietati optice

Refractia este caracterizata prin indicele de refractie de referinta n_d sau n_e (coloana B sau C), iar dispersia prin numarul Abbe n_d sau n_e (coloanele D sau E).

Pentru caracterizarea completa a dispersiei sunt redati coeficientii polinomului de interpolare Sellmeier fara termen liber, de forma:

. (5.1)

Coloanele G-L indica valorile coeficientilor B_{1, 2, 3}, C_{1, 2, 3}.

In functie de sarja, producatorul asigura indici de refractie cu abateri la a patra zecimala si numere de dispersie cu abateri la a treia zecimala.

In figura 5.3 sunt prezentate tolerantele indicelui de refractie de referinta si a numarului Abbe, pentru patru categorii de calitate.

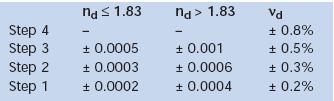
Fig. 5.3. Tolerantele indicelui de refractie de referinta

si a numarului Abbe

Clasele de calitate pentru sticla tratata prin recoacere si semifabricatele presate sunt definite in figurile 5.4 si 5.5.

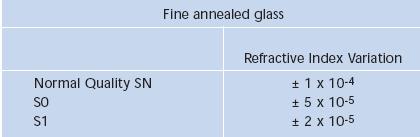
Fig. 5.4. Valorile tolerantei la indicele de refractie de referinta pentru sticla tratata prin recoacere

Fig. 5.5. Valorile tolerantei la indicele de refractie de referinta pentru semifabricate presate

Masurarea indicilor de refractie si determinarea indirecta a parametrilor de dispersie se face prin refractometrie. Sunt utilizate aparate special destinate de tipul refractometrului Abbe, Pulfrich etc.

Catalogul Schott pune la dispozitie indicii de refractie pentru cele mai utilizate linii spectrale etalon prezentate in figura 5.6. Valorile sunt inscrise in coloanele DM . EI.

Transmitanta este indicata pentru toate liniile spectrale si pentru doua grosimi ale probei (25 si 10 mm) in coloanele AL . CS ale catalogului.

Determinarea transmitantei spectrale pentru alte grosimi decat cele standardizate se realizeaza pe baza relatiei:

sau , (5.2)

unde d₁, ₂ reprezinta grosimile esantioanelor comparate.

Dispersiile medii si partiale

sau

sunt inscrise in coloanele EJ . FB.

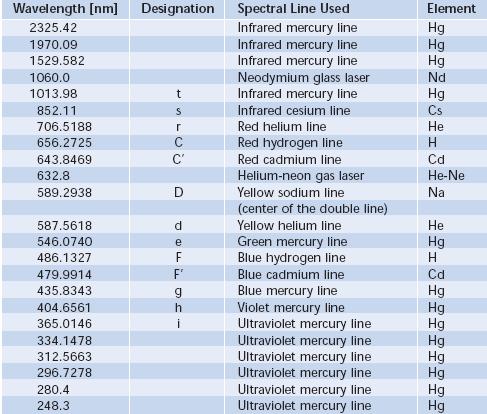
Fig.5.6. Tabloul liniilor spectrale pentru care se determina

indici de refractie

5.4. Codul de culoare

Codul de culoare contine doua cifre care indica lungimile de unda rotunjite la 10 nm si fara ultimul digit (0) la care transmitanta este 80%, respectiv 5%. De exemplu codul de culoare 33/30 semnifica t_{330 nm}=80% si t_{300 nm}

Pentru sorturile cu indice mare (marcate cu *) codul de culoare se refera la transmitantele de 70% si 5%, datorita pierderilor mari prin reflexie, care le caracterizeaza.

Codul de culoare este indicat in catalog in coloana F.

Masurarea transmitantelor se face prin utilizarea spectrofotometriei.

5.5. Coeficientul de tensiune optica

Tensiunea de birefringenta este exprimata ca diferenta de drum pe grosimea esantionului de proba:

, (5.4)

unde K - coeficientul tensiunii optice, exprimat in 10^-6 mm²/N,

d - grosimea esantionului in cm

s - tensiunea masurata in N/mm².

In figura 5.7 sunt prezentate valori ale tensiunilor de birefringenta pentru trei calitati de sticla si doua game de dimensiuni ale probei.

Valorile coeficientului tensiunilor K, este inscris in coloana DL a catalogului Schott.

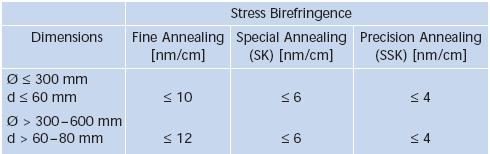
Fig. 5.7. Valori ale tensiunilor de birefringenta

Masurarea tensiunii de birefringenta se face conform ISO 11455 prin metoda Sénarmont-Friedel, care prevede masurarea diferentei de drum optic la distanta de 5% din diametrul probei in raport cu marginea acesteia sau la 5% din dimensiunea cea mai mare fata de o muchie pentru o proba de forma prismatica.

5.6. Proprietati chimice ale sticlelor optice

Rezistenta climatica este reglemetata prin standardul ISO/WD 13384, care indica metodele de incercare si clasele de rezistenta CR 1 . 4.

Temperatura si umiditatea ridicate determina formarea unui strat subtire cu aspect opac, care micsoreaza transmitanta sticlei. Prin incercari accelerate, constand in expunerea probelor timp de 30 ore intr-o camera climatizata, la temperaturi de 40 . 50^oC, sorturile sunt clasificate dupa pierderile de transmitanta (fig. 5.8).

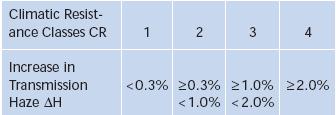
Fig. 5.8. Clasele de rezistenta climatica a sticlelor optice

Stabilitatea la solutii diluate de acid in apa se determina prin masurarea timpului, in ore, la care apar pete de coroziune albastre sau maronii, la contactul sticlei cu una dintre solutiile de testare standardizate: solutia I (acid acetic cu pH=4.6) si solutia II (acetat de sodiu cu pH=5.6), la temperatura de 25^oC.

Se apreciza ca aparitia petelor vizibile corespunde unei grosimi a stratului afectat de 0.1 µm.

Cele 5 clase de stabilitate la solutii slab acide sunt descrise in figura 5.9.

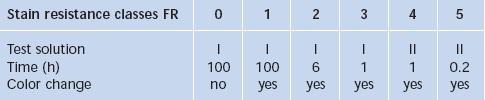
Fig. 5.9. Clasele de calitate privind rezistenta la solutii slab acide

Rezistenta la acizi este relementata prin ISO 8424 si ISO 1987 si defineste clasele SR 1-4, 5, 51-53. Rezistenta la acizi este simbolizata prin trei caractere: primele doua indica rezistenta propriu-zisa la acizi, iar al treilea caracter arata daca suprafata atacata are urme de coroziune vizibile cu ochiul liber. Masurarea rezistentie la acizi se realizeaza prin determinarea timpului necesar pentru disolvarea unei grosimi de 0.1 µm. Solutiile utilizate sunt un acid puternic (acid azotic, c=0.5 mol/l, pH = 0.3) pentru sticlele mai rezistente si acid acetic, cu pH = 4.6, pentru sticlele mai putin rezistente la acizi. Incercarile se desfasoara la 25^oC.

Figura 5.10 prezinta clasele de rezistenta la acizi si caracteristicile lor.

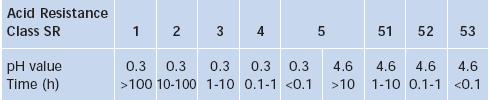
Fig. 5.10. Clasele de incadrare a sticlelor optice functie de rezistenta la acizi

Rezistenta la substante alcaline (ISO 10629) incadreaza sticlele optice in 4 clase :AR 1-4, iar rezistenta la fosfati (ISO 9698) in alte patru clase: PR 1-4. Cele doua caracteristici sunt simbolizate prin doua cifre, separate cu virgula. Prima cifra indica rezistenta in ore, iar a doua arata daca petele de material transformat chimic sunt vizibile cu ochiul liber.

Pentru determinarea rezistentei la substante alcaline se utilizeaza o solutie de hidroxid de sodiu (c=0.01 mol/l, pH=12), la 50^oC si se masoara timpul in care solutia corodeaza 0.1 µm din material. Similar, pentru rezistenta la fosfati se utilizeaza pentafosfat de sodiu (Na5P3O10, c = 0.01mol/l, pH = 10).

Clasele AR si PR sunt descrise in figura 5.11.

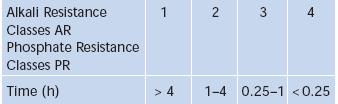
Fig. 5.11. Clasele de rezistenta la alcali si fosfati a sticlelor optice

Clasele caracteristice pentru FR, SR, AR si PR contin un digit alocat indicarii coloratiei superficiale. Valoarea acestui digit poate fi 0, 1, 2, 3, 4, dupa cum urmeaza:

.0 fara urme vizibile

.1 suprafata curata, dar cu neregularitati

.2 coloratie superficiala

.3 strat subtire albicios puternic aderat la suprafata

.4 strat deteriorat gros cu aderenta mica, cu aspect de crusta.

In catalogul Schott rezistenta chimica a sorturilor este indicata in coloanele CU . CY.

5.7. Proprietati mecanice ale sticlelor optice

Duritatea Knoop este masurata conform standardului ISO 9385, care indica aplicarea unei forte de 0.9807 N, timp de 20 s, prin intermediul unui penetrator de diamant.

In catalogul Schott microduritatea Knoop (KH) este indicata in coloana DJ.

Prelucrabilitatea cu diamant este determinata conform ISO 12844, prin polisarea probelor timp de 30 s, iar volumul de material indepartat este raportat la sortul de referinta N-SK16, pentru care se considera valoarea normata 100. Clasele de prelucrabilitate (HG) sunt redate in figura 5.12.

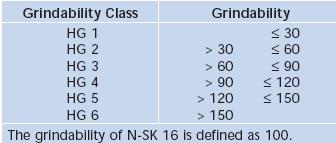
Fig. 5.12. Clasele de prelucrabilitate a sticlelor optice

In catalogul Scott HG este indicata in coloana DK. Coloanele DH si DI contin valorile modulului de elasticitate E si a coeficientului Poisson (m

In coloana CZ este specificata densitatea masica in kg/dm³.

5.8. Proprietati termice ale sticlelor optice

Functie de temperatura, vascozitatea sticlelor se incadreaza in trei domenii. In stare topita, sticla are vascozitatea mai mica decat 10 dPa.s. Valorile cresc in timpul racirii si solidificarii, faza plastica fiind caracterizata de domeniul de valori (10 . 10¹³) dPa.s. La temperatura de tragere (T₁₀^7.6), sticla are vascozitatea 10^7.6 dPa.s. Sub temperatura de formare T₁₀¹³, la care tensiunile interne se egalizeaza in cca 15 minute, sticla este considerata solida. Temperatura de formare Tg se determina conform ISO 7884-8. Temperaturile corespunzatoare vascozitatii 10¹³, 10^7.6 si Tg sunt redate in catalog in coloanele DA, DB si DC.

Coeficientii de dilatare termica, pe diverse intervale de temperatura sunt indicati in catalog in coloanele DF si DG.

Conductivitatea termica este incrisa in coloana DE (masurata in W/(mK), iar capacitatea calorica in coloana DD (exprimata in J/(gK)).

5.9. Clasificari ISO privind calitatea semifabricatelor

din sticla optica

Incadrarea in categorii privind continutul de bule se face conform ISO 10110, prin masurarea ariei bulelor existente intr-un volum de 100 cm³. Incluziunile sunt tratate in aceeasi maniera ca si bulele. Evaluarea se face luand in considerare defectele cu diametru >0.03 mm.

Clasele de incadrare a sticlelor optice pe criteriul bulelor si incluziunilor sunt prezentate in figura 5.13. In catalogul Schott clasa sorturilor este indicata pe coloana CT.

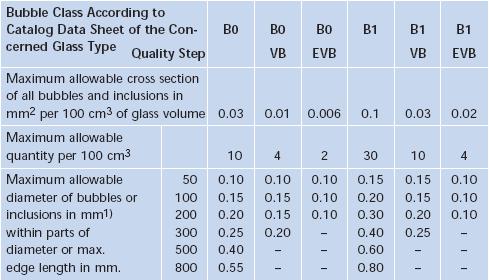
Fig. 5.13. Clase de bule si incluziuni ale sticlelor optice

Omogenitatea sticlelor este apreciata prin variatia indicelui de refractia, determinata cu relatia:

, (5.5)

unde DW - deformatia frontului de unda cu traseu birefringent, masurata in numar de lungimi de unda. Determinarea de face interferometric, in lumina monocromatica furnizata de un laser He-Ne (633 nm)

d - grosimea piesei.

In figura 5.14 sunt inscrise clasele de omogenitate si caracteristicile lor.

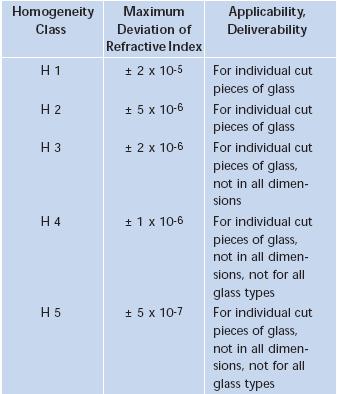
Fig.5.14. Clase de omogenitate a sticlelor optice

Semifabricatele din sticla optica pot fi blocuri prismatice sau cilindrice de sticla tratata prin recoacere. Dimensiunile si tolerantele standardizate ale acstora sunt redate in figurile 5.15 si 5.16.

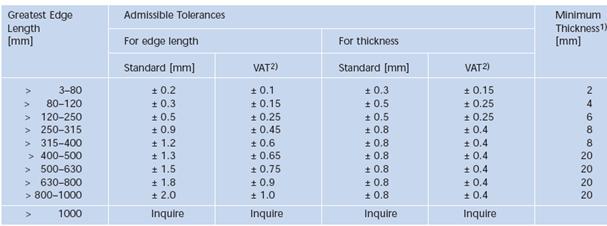
Fig.5.15. Dimensiunile si tolerantele semifabricatelor prismatice

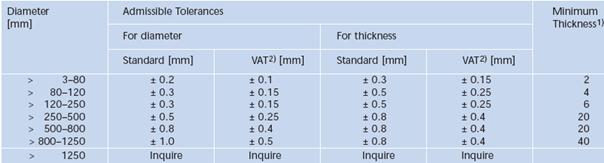
Fig. 5.16. Dimensiunile si tolerantele semifabricatelor cilindrice

Tabloul din figura 5.17 prezinta dimensiunile si tolerantele semifabricatelor cilindrice carotate de precizie.

Fig. 5.17. Dimensiunile si tolerantele semifabricatelor carotate

Pentru productia de lentile de ochelari sau componente mai putin pretentioase se utilizeaza semifabricate presate, ale caror dimensiuni si tolerante sunt prezentate in figura 5.18.

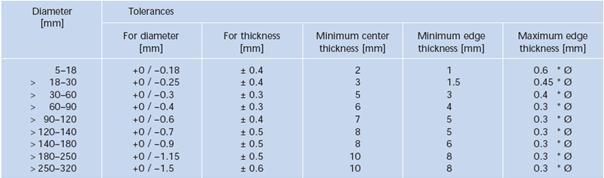
Fig. 5.18. Dimensiunile si tolerantele semifabricatelor presate

6.Tehnologia depunerii straturilor subtiri si straturi antireflex

Teoria acoperirii cu strat subtire antireflex este de fapt inspirata de teoria filtrelor interferentiale. Astfel de filtre sunt folosite sa transmita lumina monocromatica (o singura lungime de unda). Constructia initiala a filtrului interferential este prezentata in figura 6.1.

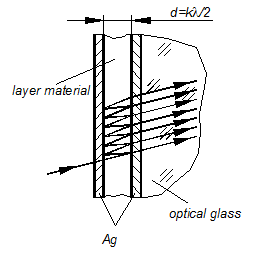
Fig.6.1

Un material optic subtire este invelit cu trei straturi: Ag, un material special, care de fapt de obicei este MgF₂ si din nou un strat de Ag. Straturile de Ag sunt atat de subtiri astfel incat sa fie semitransparente(cu reflexie partiala si transmisie partiala).

Ideea este ca o raza de lumina incidenta pe suprafata filtrului va fi impartita in multe raze transmise si reflectate. Razele care strabat filtrul sunt coerente doar pentru o anumita lungime de unda care depinde de diferenta caii optice (OPD) si ele interfereaza producand lumina monocromatica transmisa. Lungimea de unda pe care interferenta este constructiva (da un maxim de iluminare) in functie de grosimea d a stratului de mijloc.

Conditia dimensionarii pentru grosimea stratului pentru o anumita lungime de unda l este ceruta:

(6.1)

Considerand primul ordin de spectru, care contine cea mai mare parte de energie (k=1) rezulta:

, (6.2)

unde n este indicele de refractie a stratului de mijloc.

Acesta este o metoda simpla (teoretic) de obtinere a luminii monocromatice foarte precisa (Dl<10Ĺ) folosind doar un singur tip de material, dar la o grosime diferita. Tehnologia de obtinere este complicata deoarece este necesar sa se controleze foarte exact grosimea stratului, care este intr-adevar foarte mica (de ordinul lungimii de unda). Totusi exista tehnologii de producere a filtrelor interferentiale pentru radiatia monocromatica in orice regiune a spectrului electromagnetic (de la razele X pana la MW).

Toleranta in invelirea cu straturi subtire sunt in marja de l l

Invelisurile AR sunt tratate intr-un mod similar. Diferenta consta in conditia folosita pentru dimensionarea grosimii stratului. Dimensionarea este bazata pe o idee de interferenta distructiva a razelor rezultate prin multiple reflectii succesive, in asa fel incat energie lor pierduta sa dobandita de lumina transmisa.

In cazul invelisurilor AR conditia matematica pentru interferenta distructiva (minimum de iluminare) este:

(6.3)

Pentru k=1 rezulta grosimea:

, (6.4)

unde l este lungimea de unda pentru care reflectia trebuie eliminata si n este indicele de refractie al stratului.

Sistemul functioneaza daca reflectantele suprafetelor aer/strat si strat/sticla (deoarece nu se mai foloseste strat Ag subtire ), care din punct de vedere matematic inseamna:

, (6.5)

sau . (6.6)

Relatia (6) arata ca indicele de refractie al stratului trebuie sa fie mai mic decat cel al indicelui sticlei si un material adecvat trebuie gasit pentru fiecare tip de sticla.

Lentilele oftalmologice sunt invelite cu TiO₂ si grosimea este calculata pentru l=555nm, la mijlocul spectrului vizibil. Asta inseamna ca, deci, culoarea verde-galbena este indepartata din lumina reflectata, deci lentilele au o culoar specifica de albastru-violet.

Imbunatatirea reflectanta globala (in lumina alba) este posibila prin invelirea cu multi-straturi (pentru mai multe de o lungime de unda)

In acest caz, indicele de refractie a straturilor trebuie sa corespunda conform urmatoarelor relatii:

, (6.7)

Pentru doua straturi si :

, (6.8)

Pentru trei straturi (stratul 1 - cel exterior, stratul 2 - cel din mijloc, stratul 3 - cel de langa sticla).

Fig. 6.2 Schema de principiu

Lentilele, dupa operatia finala de spalare si uscare, sunt introduse intr-o incinta etansa a istalatiei. Procesul de depunere a straturilor consta din mai multe faze:

in prima faza, de pregatire a suprafetelor de sticla minerala sau organica, se urmareste eliminarea tuturor impuritatilor solide si a moleculelor de apa, care se mai pot afla pe lentile; pentru aceasta, in incinta se creeaza un vid de (10^-5 . 10^-6)mbar si o temperatura de -135^oC; curatirea propriu-zisa este realizata prin bombardarea suprafetelor cu ioni de Argon, obtinuti cu ajutorul unui dispozitiv numit tun ionic; procesul are si un efect similar sablarii, dar la scara moleculara, asigurandu-se astfel o buna aderenta a straturilor depuse

in faza urmatoare, prin efect termic al curentului electric, este topit si vaporizat controlat continutul nacelei cu materialul care trebuie depus in primul strat;

in functie de numarul straturilor necesare sunt reluate fazele descrise anterior.

Lentilele utilizate ca probe au fost produse la firma Interoptik SRL Timisoara, care utilizeaza o masina C 250 (de fabricatie elvetiana) de depunere a straturilor subtiri.

In figurile urmatoare sunt prezentate cateva imagini preluate in timpul pregatirii si desfasurarii unui proces tehnologic de depunere.

Fig. 6.3.Camera curata de pregatire a lentilelor pentru introducerea in instalatia de depunere a straturilor subtiri

Fig. 6.4.Suportul cu lentile pozitionat pentru coborare in incinta instalatiei

Fig.6.5.Suport rotativ cu nacele care contin materialele de depus (prin topire locala si vaporizare)

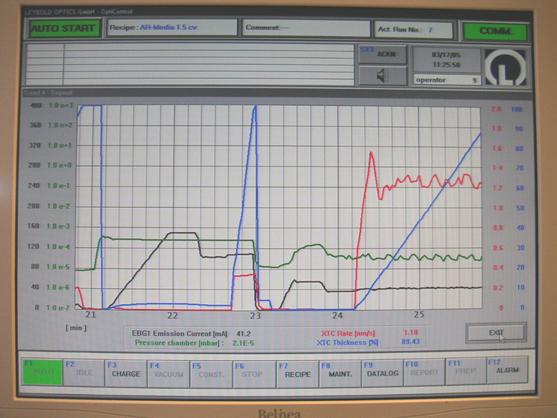
Fig.6.6 Display al instalatiei pentru monitorizarea procesului de depunere (linia verde indica presiunea din incinta - ~10^-5mbar-, linia rosie indica viteza de depunere [nm/s], linia albastra arata grosimea stratului depus [nm])

Pentru lentilele din sticla minerala se pot doua sau trei straturi. Primul strat are rolul antireflex pentru lungimea de unda de 555 nm. Al doilea strat poate fi direct cel final, exterior numit "strat clean", care este constituit dintr-un material antistatic si nehigroscopic sau poate fi un al doilea strat antireflex, pentru o lungime de unda din zona violetului (400nm). Al treilea strat este totdeauna stratul clean.

In primul caz (antireflex pentru 555 nm si strat clean) acoperirea se numeste antireflex mediu (simbol AR-M); culoarea suprafetei lentilei tratate AR-M este complementara lungimii de unda dominante pentru care s-a suprimat reflexia (albastru-violet).

In al doilea caz (antireflex pentru 555 nm, 400 nm si strat clean), acoperirea se numeste antireflex super (simbol AR-S); culoarea suprafetei lentilei este verde.

In figura urmatoare se poate vedea diferenta de culoare a lentilelor, prin care un observator poate identifica prezenta acoperirii antireflex si a tipului de acoperire.

Fig.6.7. Diferenta de culoare a lentilelor cu strat antireflex

Pentru lentilele din sticla organica se depune un strat suplimentar, de durificare a suprafetei. Materialul utilizat este SiO₂ si se depune ca baza (este intotdeauna primul strat).

Instalatia de depunere C 250 reprezinta un model de ultima ora in domeniu, cu performante deosebite privind productivitatea (cca. 22 min/ciclu) si consumul de energie.