 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
Modele reologice
1. Modelul fluidului newtonian
Fluidul newtonian este un fluid de ordinul intai a carui ecuatie constitutiva este de forma ecuatiei ( 3.7). Raportata la sistemul de coordonate carteziene plan ecuatia constitutiva are forma:
![]() (3.23)
(3.23)
deoarece ![]() in care
in care ![]() este viscozitatea
dinamica a fluidului newtonian. Sub forma tensoriala ecuatia constitutiva are
forma:
este viscozitatea
dinamica a fluidului newtonian. Sub forma tensoriala ecuatia constitutiva are
forma:
![]() (3.24)
(3.24)
2. Modelul fluidelor nenewtoniene
Forma generala a ecuatiei constitutive pentru fluide nenewtoniene incompresibile este de forma:
![]() (3.25)
(3.25)
in care ![]() este "viscozitatea"
fluidului.
este "viscozitatea"
fluidului.
Ecuatia
(3.25) nu descrie dezvoltarea si relaxarea eforturilor normale in curgeri de
forfecare simple, deoarece ![]() se anuleaza
instantaneu daca
se anuleaza
instantaneu daca ![]() = 0, deci la indepartarea deformatiei. Daca numai
componentele de forfecare ale lui
= 0, deci la indepartarea deformatiei. Daca numai
componentele de forfecare ale lui ![]() sunt nenule , ca in
curgerea de forfecare simpla, atunci singurele componente nenule ale lui
sunt nenule , ca in
curgerea de forfecare simpla, atunci singurele componente nenule ale lui ![]() sunt de asemenea cele
de forfecare, deoarece
sunt de asemenea cele
de forfecare, deoarece ![]() este definita drept o
cantitate scalara.
este definita drept o
cantitate scalara.
In consecinta, fluidul nu dezvolta eforturi normale intr-0 curgere de forfecare simpla. Din ecuatia (3.7) rezulta:
![]() (3.26)
(3.26)
unde ![]() .
.
Intre
invariantul direct al tensorului ![]() simetric:
simetric:
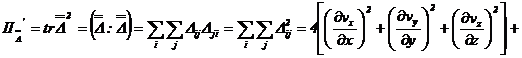
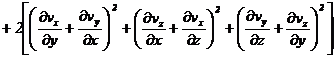 (3.27)
(3.27)
si invariantul compus al tensorului ![]() simetric exista
relatia:
simetric exista
relatia: ![]() valabila pentru fluide
incompresibile.
valabila pentru fluide
incompresibile.
In locul
invariantului ![]() se poate utiliza
marimea lui
se poate utiliza
marimea lui ![]() :
:
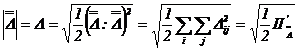 (3.28)
(3.28)
si deci
![]() (3.29)
(3.29)
Modelul "legea puterii" sau Ostwald de Waele.
Pentru acest model viscozitatea aparenta este data de relatia:
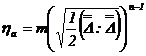 (3.30)
(3.30)
in care ![]() este indicele de
consistenta cu dimensiunea
este indicele de
consistenta cu dimensiunea ![]() si
si ![]() este indicele de
curgere ( exponentul legii puterii ) adimensional.
este indicele de
curgere ( exponentul legii puterii ) adimensional.
Intr-o
reprezentare dublu logaritmica ![]() respectiv
respectiv ![]() pentru curgerea
unidirectionala rezulta o dreapta. Multe fluide prezinta o astfel de comportare
cel putin pe o decada de valori a vitezei de deformare prin forfecare, iar pe
mai multe decade reprezentarea poate fi o curba.
pentru curgerea
unidirectionala rezulta o dreapta. Multe fluide prezinta o astfel de comportare
cel putin pe o decada de valori a vitezei de deformare prin forfecare, iar pe
mai multe decade reprezentarea poate fi o curba.
Variatia
viscozitatii aparenta in raport cu viteza de deformare prin forfecare, figura
3.5. prezice o valoare infinita a viscozitatii aparente, pentru fluide
pseudoplastice ![]() cand viteza de
deformare tinde spre zero si o valoare infinita pentru fluide dilatante
cand viteza de
deformare tinde spre zero si o valoare infinita pentru fluide dilatante ![]() cand viteza de
deformare tinde spre infinit, ceea ce nu corespunde observatiilor
experimentale. Aceleasi anomalii se constata la viteze de deformare tinzand
spre infinit pentru fluide pseudoplastice si spre zero pentru fluide dilatante,
cand viscozitatea aparenta ar trebui sa se anuleze. Deci, ecuatia (3.30) nu
descrie extremitatile curbei, viscozitatile respective rezultand prin
extrapolare, figura 3.6.
cand viteza de
deformare tinde spre infinit, ceea ce nu corespunde observatiilor
experimentale. Aceleasi anomalii se constata la viteze de deformare tinzand
spre infinit pentru fluide pseudoplastice si spre zero pentru fluide dilatante,
cand viscozitatea aparenta ar trebui sa se anuleze. Deci, ecuatia (3.30) nu
descrie extremitatile curbei, viscozitatile respective rezultand prin
extrapolare, figura 3.6.
Exemple de fluide pseudoplastice: suspensii de particule asimetrice; solutii ale polimerilor derivati de la celuloza ( hidroxi etil celuloza (HEC), carboxi metil celuloza (CMC) ); ciment; maioneza; suspensii de detergenti.
Cu toate deficientele semnalate, ecuatia este mult utilizata, avand o forma algebrica simpla si continand numai doi parametri ( constante ajustabile ).
Pentru curgerea unidirectionala ecuatia constitutiva a modelului Ostwald de Waele are expresia:
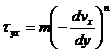 . sau
. sau ![]() (3.31)
(3.31)
Parametrii modelului Ostwald de Waele nu vor depinde de geometria in care au fost determinati, deci conditia de invarianta la transformarea axelor de coordonate devine acum usor de inteles.
Parametrii
modelului Ostwald de Waele pot fi determinati dintr-un set de date
experimentale ![]() , reprezentand grafic
, reprezentand grafic ![]() intr-o diagrama dublu
logaritmica,
intr-o diagrama dublu
logaritmica, ![]() functie de
functie de ![]() .figura 3.4.
.figura 3.4.
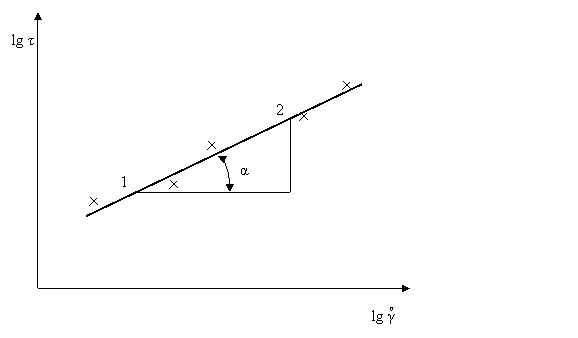
Fig.3.4. Determinarea parametrilor modelului Ostwald de Waele
din date experimentale
Prin logaritmarea ecuatiei (3.31) se liniarizeaza:
![]()
Se
considera doua puncte pe dreapta ce aproximeaza cel mai bine datele
experimentale, ![]() si
si ![]() si se calculeaza panta
dreptei:
si se calculeaza panta
dreptei:
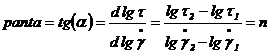
din care rezulta unul din parametrii, indicele de curgere ![]() . Celelalt parametru , indicele de consistenta
. Celelalt parametru , indicele de consistenta ![]() se determina din
relatia:
se determina din
relatia:
![]()
![]()

Fig.3.5. Variatia viscozitatii aparente Fig.3.6. Valorile extrapolate ale
functie de viteza de deformare viscozitatii aparente
prin forfecare:
1 - fluid pseudoplastic;
2 - fluid dilatant
Aplicatia 3.1.
Datele masuratorilor reologice
pentru o solutie apoasa 1 % guma la ![]() sunt prezentate in
tabelul . Sa se determine
parametrii modelului legii puterii si sa se reprezinte grafic variatia
viscozitatii aparente in raport cu viteza de deformare prin forfecare.
sunt prezentate in
tabelul . Sa se determine
parametrii modelului legii puterii si sa se reprezinte grafic variatia
viscozitatii aparente in raport cu viteza de deformare prin forfecare.
|
Nr. exp. |
|
|
|
|
1. |
9,88 |
2,61 | |
|
2. |
11,4 |
2,97 | |
|
3. |
12,0 |
2,81 | |
|
4. |
14,1 |
3,44 | |
|
5. |
17,6 |
3,80 | |
|
6. |
26,3 |
4,85 | |
|
7. |
42,0 |
6,61 | |
|
8. |
48,6 |
6,19 | |
|
9. |
49,3 |
5,89 | |
|
10. |
55,5 |
7,22 | |
|
11. |
58,8 |
8,20 | |
|
12. |
75,4 |
9,08 | |
|
13. |
104,1 |
11,63 | |
|
14. |
110,4 |
10,65 | |
|
15. |
120,5 |
12,75 | |
|
16. |
136,5 |
13,10 | |
|
17. |
145,8 |
14,90 | |
|
18. |
187,1 |
15,85 | |
|
19. |
210,2 |
12,70 | |
|
20. |
270,0 |
20.50 |
Rezolvare:

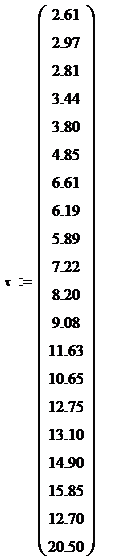
![]()
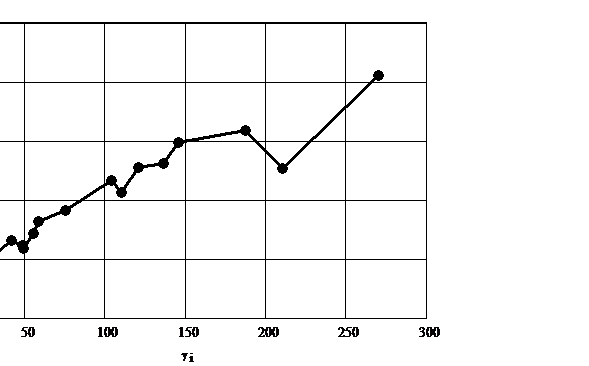
 Fig. 3.7. Variatia efortului de forfecare
functie de viteza de deformare prin
Fig. 3.7. Variatia efortului de forfecare
functie de viteza de deformare prin
forfecare
Fig. 3.8. Diagrama dublu logaritmica, efort de forfecare functie de viteza de
deformare prin forfecare
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Parametrii modelului reologic sunt: indicele de curgere: n = 0,598;
indicele de consistenta: m = 0,672 ![]()
![]()
![]()
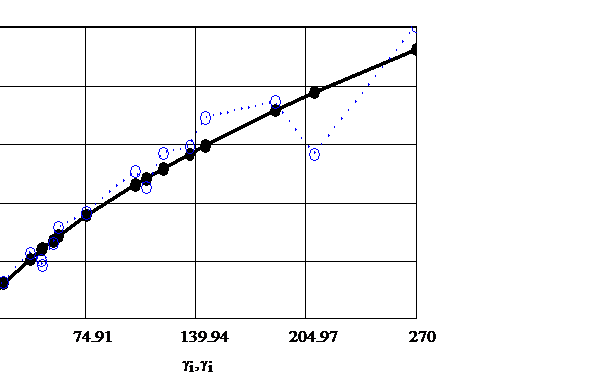
Fig. 3.9. Compararea valorilor efortului de forfecare experimental cu cel
calculat functie de viteza de deformare prin forfecare


![]()
![]()

Fig.3.10. Variatia viscozitatii aparente functie de viteza de
deformare prin forfecare
Aplicatia 3.2.
Sa se determine parametri modelului Ostwald de Waele pentru urmatoarele date experimentale obtinute la extrudarea polietilenei de inalta presiune la 220 C intr-o capilara:
|
Nr. exp. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
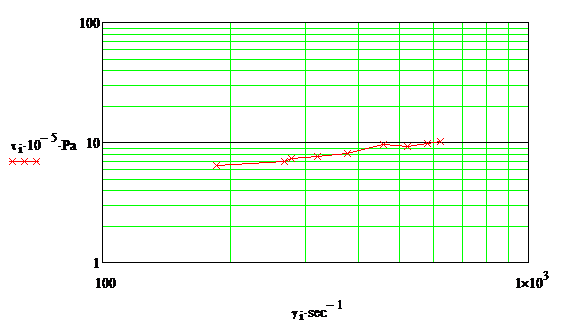
Efortul de forfecare,
|
6,48 |
6,91 |
7,34 |
7,59 |
8,05 |
8,71 |
9,24 |
9,73 |
10,1 |
|
Viteza de
deformare, |
185,2 |
267,6 |
277,1 |
320,0 |
376,4 |
455,5 |
520,1 |
579,3 |
621,1 |
Rezolvare:

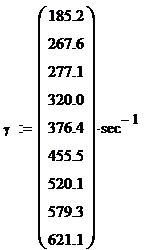
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
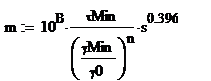
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
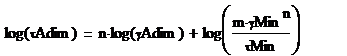
![]()
![]()

![]()
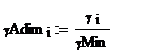
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


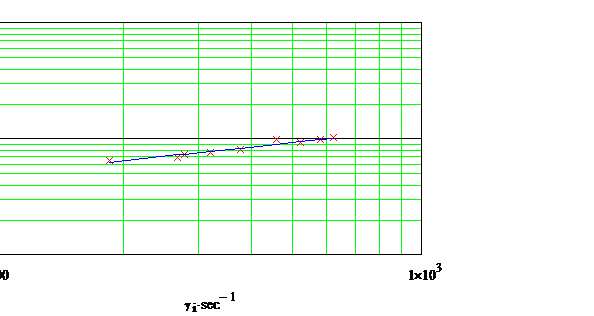
Experimental se pot determina cele
doua viscozitati, viscozitatea aparenta la viteza de deformare nula ![]() si viscozitatea
aparenta la viteza de deformare infinita
si viscozitatea
aparenta la viteza de deformare infinita ![]() pentru un fluid pseudoplastic
masurand viteza de deformare functie de efortul de forfecare, figura 3.7.
pentru un fluid pseudoplastic
masurand viteza de deformare functie de efortul de forfecare, figura 3.7.
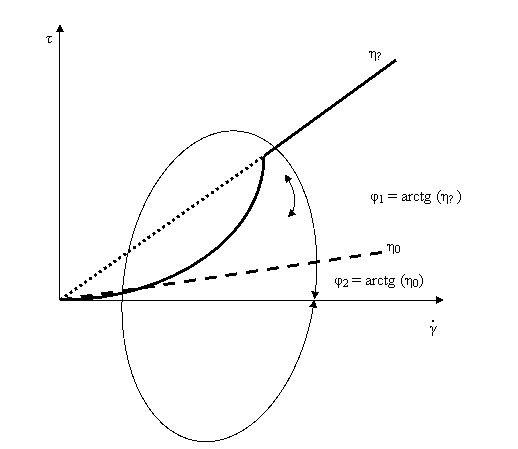
Fig.3.7. Variatia vitezei de deformare functie de efortul
de forfecare pentru un fluid pseudoplastic
Modelele Ellis si Sisko
Modelele empirice cu mai mult de doi parametri permit calculul viscozitatii limita in conditii extreme de forfecare, de exemplu modelul Ellis si modelul Sisko. Modelul Ellis permite estimarea in cazul fluidelor pseudoplastice a viscozitatii limita la eforturi de forfecare mici si in cazul fluidelor dilatante, a viscozitatii limita la eforturi de forfecare mari. Modelul Ellis este valabil numai pentru fluide pseudoplastice si permite calculul viscozitatii limita la eforturi de forfecare mari. Ecuatiile constitutive au urmatoarele expresii:
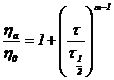 modelul
Ellis (3.32)
modelul
Ellis (3.32)
![]() modelul
Sisko (3.33)
modelul
Sisko (3.33)
in care:
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Determinarea parametrilor modelului Ellis se face prin liniarizarea ecuatiei (3.32) care se scrie sub forma:
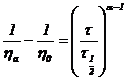 sau
sau 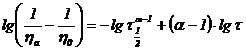 .
.
In cazul in care se dispune de un
set de date experimentale ![]() si se reprezinta
grafic intr-o diagrama dublu logaritmica
si se reprezinta
grafic intr-o diagrama dublu logaritmica 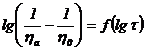 se obtine o dreapta.
Din panta dreptei se obtine
se obtine o dreapta.
Din panta dreptei se obtine ![]() , figura 3.8:
, figura 3.8:
Se
considera doua puncte pe dreapta ce aproximeaza cel mai bine datele experimentale,
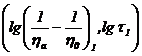 si
si 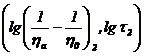 si se calculeaza panta
dreptei:
si se calculeaza panta
dreptei:
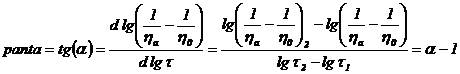
iar parametrul ![]() rezulta din relatia:
rezulta din relatia: 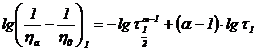 .
.

Fig.3.8. Determinarea parametrilor Ellis din date experimentale
Determinarea parametrilor modelului Sisko se face prin liniarizarea ecuatiei (3.33) care se scrie sub forma:
![]()
In cazul in care se dispune de un
set de date experimentale ![]() si se reprezinta
grafic intr-o diagrama dublu logaritmica
si se reprezinta
grafic intr-o diagrama dublu logaritmica ![]() se obtine o dreapta.
Din panta dreptei se obtine indicele de
curgere
se obtine o dreapta.
Din panta dreptei se obtine indicele de
curgere ![]() , figura 3.9:
, figura 3.9:
Se
considera doua puncte pe dreapta ce aproximeaza cel mai bine datele
experimentale, ![]() si
si ![]() si se calculeaza panta
dreptei:
si se calculeaza panta
dreptei:
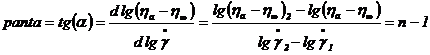
iar parametrul ![]() rezulta din relatia:
rezulta din relatia: ![]() .
.

Fig.3.9. Determinarea parametrilor modelului Sisko din date experimentale
Modelul Bingham
Modelul Bingham are urmatoarea expresie a ecuatiei constitutive:
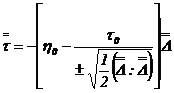 pentru
pentru ![]() (3.34)
(3.34)
![]() pentru
pentru ![]() (3.35)
(3.35)
in care:
![]() reprezinta pragul de
curgere.
reprezinta pragul de
curgere.
Pentru curgerea simpla a fluidelor incompresibile , ecuatia constitutiva se scrie sub forma:
![]() (3.36)
(3.36)
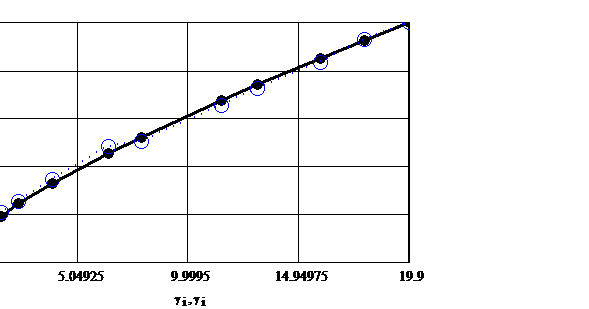
Determinarea
parametrilor modelului Bingham se face astfel: in cazul in care se dispune de
un set de date experimentale ![]() si se reprezinta
grafic intr-o diagrama obisnuita cu diviziuni echidistante
si se reprezinta
grafic intr-o diagrama obisnuita cu diviziuni echidistante ![]() se obtine o dreapta.
Din ordonata la origine se determina pragul de curgere
se obtine o dreapta.
Din ordonata la origine se determina pragul de curgere ![]() iar din panta dreptei
se obtine viscozitatea limita
iar din panta dreptei
se obtine viscozitatea limita ![]() , figura 3.10:
, figura 3.10:
Se
considera doua puncte pe dreapta ce aproximeaza cel mai bine datele
experimentale, ![]() si
si ![]() si se calculeaza panta
dreptei:
si se calculeaza panta
dreptei:
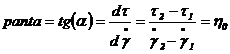
![]()
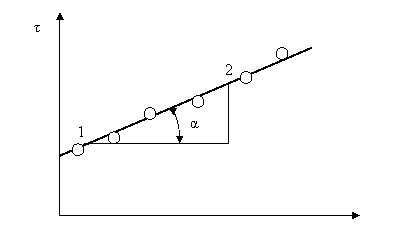
Fig.3.10. Determinarea parametrilor modelului
Bingham din date experimentale
Exemple de fluide Bingham: suspensii de particule solide; noroaie de foraj; margarina; pasta de hartie.
Aplicatia 3.3.
. O suspensie 54,6 % bentonita cu densitatea r = 1280 kg×m-3este supusa unor determinari reologice intr-un viscozimetru cu cilindri coaxiali. Se obtin urmatoarele date:
|
Nr. exp. |
1 |
2 |
3 |
4 |
5 |
|
|
100 |
150 |
250 |
325 |
400 |
|
t , Pa |
112,4 |
115,2 |
117,5 |
120,5 |
121,7 |
Sa se determine parametrii modelului Bingham ce descrie comportarea reologica a
bentonitei.
Rezolvare:
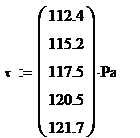

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()

![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
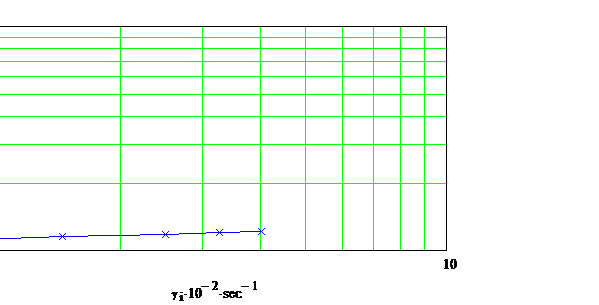
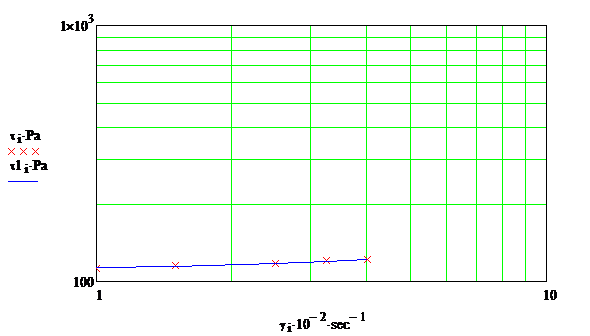 Aplicatia 3.4.
Aplicatia 3.4.
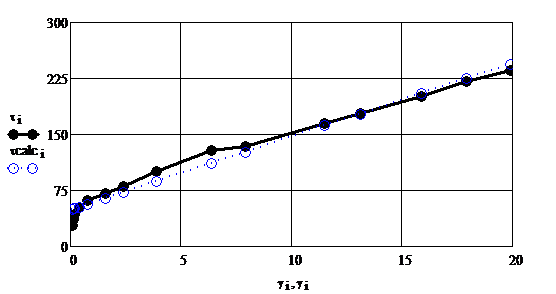
In tabelul 1 se prezinta datele
experimentale pentru ciocolata cu lapte la ![]() . Sa se determine parametrii reologici ai modelelor reologice
Bingham si Casson ce caracterizeaza pasta de ciocolata cu lapte:
. Sa se determine parametrii reologici ai modelelor reologice
Bingham si Casson ce caracterizeaza pasta de ciocolata cu lapte:
![]() - modelul
Bingham
- modelul
Bingham
![]() - modelul Casson
- modelul Casson
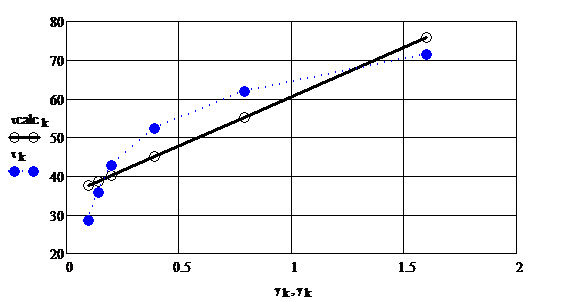
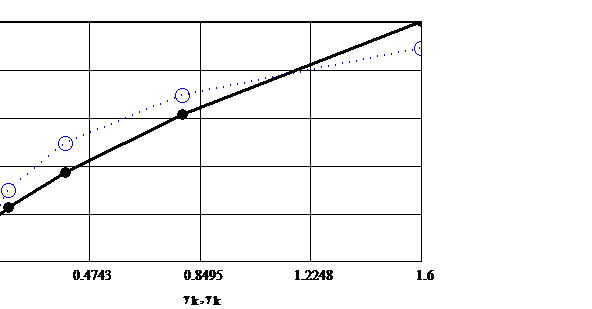
Se determina parametrii modelelor reologice pentru trei
domenii ale vitezei de deformare prin forfecare: ![]() ,
, ![]() ,
, ![]() .
.
|
Nr.exp |
1. |
2. |
3. |
4. |
5. |
6. |
7. |
8. |
9. |
10. |
|
|
0,099 |
0,14 |
0,199 |
0,39 |
0,79 |
1,6 |
2,4 |
3,9 |
6,4 |
7,9 |
|
|
28,6 |
35,7 |
42,8 |
52,4 |
61,9 |
71,4 |
80,9 |
100 |
128,3 |
133,3 |
|
11. |
12. |
13. |
14. |
15. |
|
11,5 |
13,1 |
15,9 |
17,9 |
19,9 |
|
164,2 |
178,5 |
201,1 |
221,3 |
235,6 |
Rezolvare:

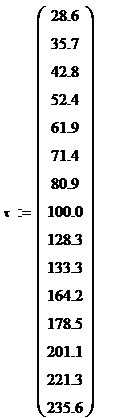
![]()
![]()
![]()
Modelul Bingham:
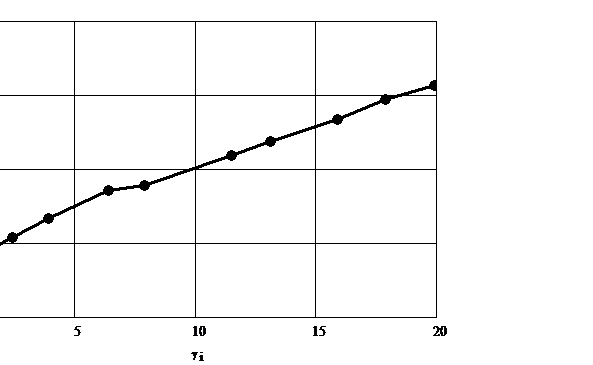
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
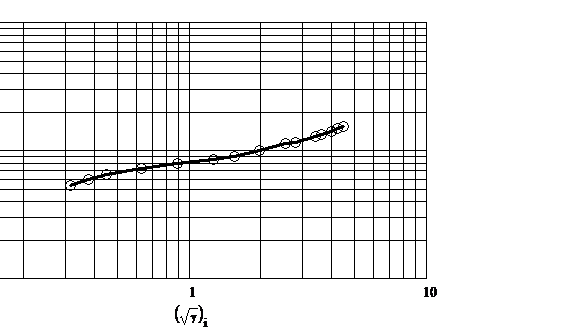
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
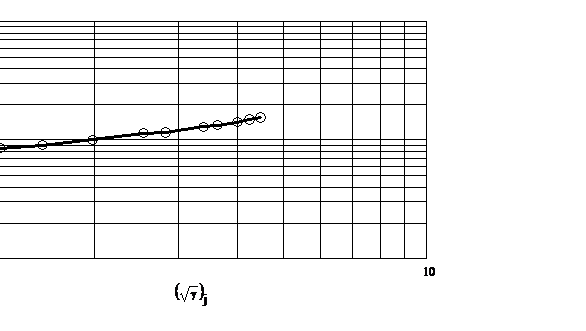
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

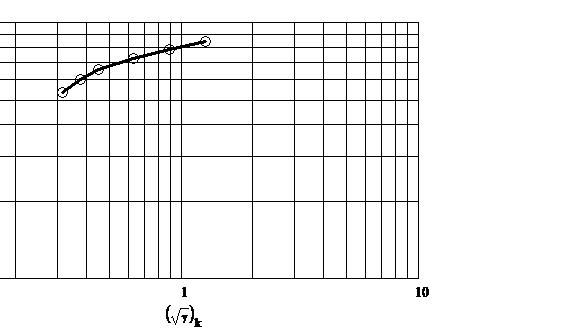
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Modelul Herschel - Bulkley
Acest model descrie compoertarea plastica si vascoasa ( nenewtoniana de tip legea puterii):
![]() (3.37)
(3.37)
in care:
![]() - reprezinta
parametrii modelului Herschel - Bulkley.
- reprezinta
parametrii modelului Herschel - Bulkley.
Modelul Prandtl - Eyring
Ecuatia constitutiva are expresia:
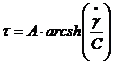 (3.38)
(3.38)
in care:
![]() reprezinta parametrii
modelului.
reprezinta parametrii
modelului.
Pentru
liniarizarea ecuatiei (3.38) se imparte prin ![]() si se aplica functia
si se aplica functia ![]() :
:
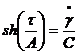 sau
sau 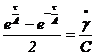 .
.
Pentru valori mari ale efortului de forfecare: ![]() rezulta
rezulta ![]() si se obtine din
ecuatia anterioara:
si se obtine din
ecuatia anterioara:
![]()
Se logaritmeaza in baza logaritm zecimal, si se obtine:
![]() sau
sau 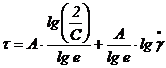 .
.
Reprezentand grafic intr-o diagrama semilogaritmica ![]() se obtine o dreapta
pentru valori mari ale efortului de forfecare, figura 3.11.
se obtine o dreapta
pentru valori mari ale efortului de forfecare, figura 3.11.
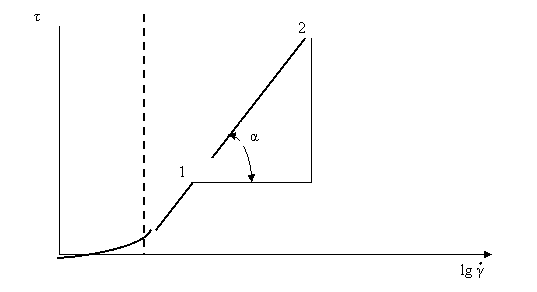
Fig.3.11. Determinarea parametrilor modelului Prandtl - Eyring
din date experimentale
![]()
Se considera doua puncte pe dreapta ce aproximeaza cel mai
bine datele experimentale, ![]() si
si ![]() si se calculeaza panta
dreptei:
si se calculeaza panta
dreptei:
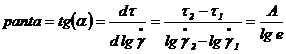
din care rezulta parametrul A.
Celalalt parametru se obtine din relatia: 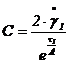 .
.
Copyright © 2024 - Toate drepturile rezervate