Reglarea automata a nivelului

Reglarea automata a nivelului

1 Estimarea parametrilor din cadrul proceselor de umplere - golire

Nivelul se regleaza in procese de umplere-golire, iar sistemul de reglare automata pentru nivel SRA-L, este reprezentat conventional ca in figura 1. Astfel, se calculeaza modelul dinamic al procesului de umplere-golire la un rezervor cu sectiune constanta S, alimentat cu debitul F_a , din care se extrage debitul F_e.

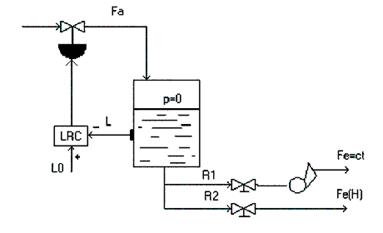
Figura 1: SRA pentru nivel (SRA-L)

unde:

L - nivelul de lichid din rezervor;

F_a - debitul de alimentare;

F_e - debitul de evacuare;

L₀ - valoarea prescrisa pentru nivel.

Se considera doua cazuri posibile:

1. evacuarea la debit constant, F_e= ct;
2. evacuarea la debit variabil, in functie de nivelul din rezervor, Fe(L).

Estimarea parametrilor acestui model se bazeaza pe ecuatia de conservare a cantitatilor de fluid care se vehiculeaza in proces.

1.1 Calculul modelului matematic pentru evacuarea la debit constant

Pentru regimul stationar (acumulare nula in sistem), cantitatea introdusa este egala cu cea extrasa din rezervor, astfel ca:

(1)

unde este debitul de alimentare, este debitul de evacuare, iar r este densitatea lichidului vehiculat.

In regimul dinamic de curgere, diferenta dintre fluxurile introdus si extras din rezervor, este compensata de cantitatea acumulata (dezafectata) in rezervor:

(2)

In (2) s-a notat prin S sectiunea rezervorului, iar prin L(t) nivelul de lichid la momentul t, M(t) reprezentand masa de lichid din rezervor la momentul t. Marimile variabile in timp din (2) se obtin prin variatii arbitrare, date peste valorile lor de regim stationar:

(3)

Din (2) si (3) rezulta:

(4)

Prin extragerea conditiei de regim stationar in (1) se obtine:

(5)

Se normeaza variatiile marimilor de interes si se obtine:

- marimea reglata

- marimea de executie

Avand aceste noi variabile adimensionale, relatia (5) devine:

(6)

iar prin integrare:

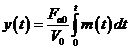(7)

Rezulta foarte usor functia de transfer a canalului de executie, de la variatia debitului de alimentare la variatia nivelului:

(8)

unde .

Exprimarea din (7) dovedeste ca procesul de umplere-golire cu evacuare la debit constant se comporta ca un element integrator, motiv pentru care se mai numeste si proces fara autostabilizare.

1.2 Calculul modelului matematic pentru evacuare la debit variabil

Pentru regimul stationar al procesului este valabila relatia (1) in care marimile isi pastreaza semnificatia. In regimul dinamic, diferenta dintre cantitatile introduse si extrase este acumulata in rezervor, dupa cum urmeaza:

(9)

Debitul F_e depinde de nivelul L din rezervor, dupa o relatie neliniara de tipul:

(10)

unde a este o constanta ce depinde de sectiunea de evacuare din rezervor, iar g este acceleratia gravitationala.

Prin dezvoltarea in serie Taylor, in jurul punctului stationar de functionare, se obtine:

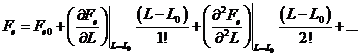(11)

Daca se trunchiaza dezvoltarea dupa partea liniara, se obtine relatia:

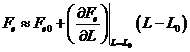(12)

valabila pentru orice L, deci la orice moment de timp t. Avem astfel:

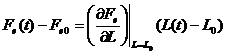(13)

sau

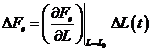(14)

Daca se reia ecuatia (9) si se considera marimile variabile in timp exprimate prin:

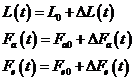
atunci avem:

(15)

Se opereaza in (15) prin extragerea regimului stationar exprimat prin (11) si se ajunge la ecuatia descrisa prin variatia marimilor de calcul:

(16)

Prin normare, se obtin marimile adimensionale ale modelului dinamic asociat canalului de executie:

- marimea reglata

- marimea de executie

Rezulta cu usurinta din (17) si prin inlocuirea derivatei lui F_e in raport cu L obtinuta din (10), ca forma finala liniarizata a ecuatiei (16) este:

(17)

Se obtine astfel, in domeniul frecventei, modelul canalului de executie in ipoteza impusa pentru procesul de umplere-golire:

(18)

in care sunt parametrii modelului matematic estimat.

Exprimarea din (17) denota faptul ca procesul de umplere-golire cu evacuare prin cadere libera (debitul variabil cu nivelul L din rezervor) se comporta ca un element de intarziere, motiv pentru care se numeste proces cu autostabilizare.

2 Proiectarea sistemelor pentru reglarea automata a nivelului

Se considera sistemul din figura 1 pentru care se cunoaste functia de transfer a partii fixate:

pentru un proces de umplere-golire fara autostabilizare (integrator), cu conditia acceptata in practica, respectiv:

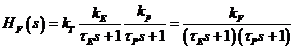pentru un proces de umplere-golire cu autostabilizare, cu parametrii de semnificatie cunoscuta.

In primul caz se recomanda un algoritm de reglare de tip P, iar in al doilea caz un algoritm de reglare de tip PI, pentru asigurarea in primul rand a unor performante de regim stationar. Cu aceste precizari, se propune pentru proiectare utilizarea unor metode bazate pe alocarea de poli-zerouri, in vederea obtinerii unor sisteme de forma standard (de ordin unu sau doi) in circut inchis. Configuratia dorita pentru repartitia polilor si zerourilor functiei de transfer a sistemelor in circut inchis exprima de fapt performantele impuse acestor sisteme fata de clasa marimilor exogene (referinte si perturbatii) considerate si ele precizate.

Astfel, pentru partea fixata din 1) se impune ca sistemul in circut inchis sa aiba o comportare exprimata prin functia de transfer corespunzatoare unui element cu intarziere de ordinul unu, de forma:

(19)

in care constanta de intarziere T se alege pentru a impune de fapt, performantele sistemului. Functia de transfer a sistemului in circut deschis este:

(20)

iar pentru sistemul in circut inchis avem:

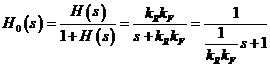(21)

Prin identificarea relatiei (19) cu (21) se obtine formula simpla de calcul:

(22)

din care, pentru cunoscut si pentru T impus, se determina factorul de amplificare al regulatorului:

(23)

Pentru partea fixata din 2) se impune ca sistemul in circuit inchis sa aiba o comportare exprimata prin functia de transfer a unui sistem de ordinul doi:

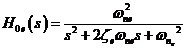(24)

la care prin dubletul se propun performantele sistemului in bucla inchisa (suprareglaj, timp de raspuns si eroare stationara).

Echivalentul functiei pentru circuitul deschis este:

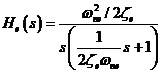(25)

Sistemul fizic in circuitul deschis are functia de transfer:

(26)

Daca se compenseaza constanta de intarziere a procesului cu constanta de timp de integrare a regulatorului T_i, adica se pune τ_P=T_i , se obtine:

(27)

Din identificarea formei (27) cu (25) rezulta relatia de proiectare care intereseaza:

(28)

si care permite determinarea factorului de amlificare al regulatorului:

(29)

unde si sunt impuse, iar si sunt date. Deci, din (29) si prin alegerea rezulta parametrii de acordare ai algoritmului PI din sistemul in bucla inchisa.

3 Implementarea sistemelor de reglare a nivelelor

Sistemele de reglare automata pentru nivel sunt realizate in structuri de reglare dupa eroare (figura 1), sau in structuri de reglare in cascada cu debitul de alimentare , care este marimea de executie, ca in figura 2:

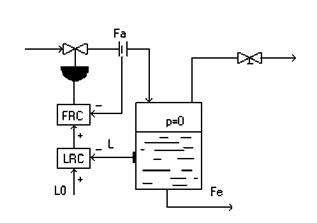
Figura 2: Reglare de nivel in cascada cu reglare de debit

Reglarea in cascada este mai eficienta daca bucla secundara de debit este mult mai rapida decat bucla principala de nivel (timpul de raspuns al SRA pentru debit se propune de circa zece ori mai mic decat timpul de raspuns al SRA pentru nivel, in faza de proiectare a structurii de cascada). Daca se respecta aceasta cerinta, perturbatiile datorate modificarii debitului de fluid sunt anihilate de bucla secundara si nu mai pot modifica marimea principala reglata, care este nivelul L.

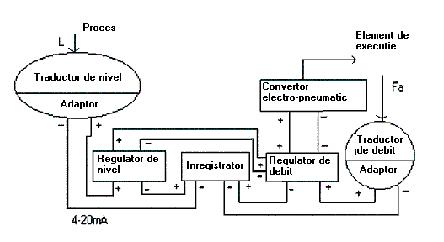
O implementare cu aparatura electronica cu semnal unificat de curent (4-20 mA) este data in figura 3 pentru o structura de reglare in cascada. Se poate constata conexiunea caracteristica de cascada, prin care regulatorul din bucla principala de nivel prescrie referinta regulatorului din bucla secundara de debit (comanda primului regulator devine marime de referinta pentru cel de al doilea regulator). Rezulta deci, ca aceasta structura, cu pretul unui efort al costului datorat traductorului de debit si regulatorului din bucla secundara, ofera un regim dinamic superior, fiind robusta la

perturbatiile datorate modificarilor arbitrare ale debitului de alimentare.

Figura 3: SRA (cascada) pentru nivel cu aparatura cu semnal unificat de curent