Pentru un motor avand urmatoarele caracteristici: m.a.c. in patru timpi cu 6 cilindri in linie si: S =125, 24 mm; P_e = 159 kW; n_P = 2100 rot/min; M_e = 74, 5 daN.m; n_M = 1400 rot/min; e = 17; p_e = 8, 8; D = 101 mm, sa se calculeze marimile caracteristice, sa se efectueze calculul cinematic si dinamic si calculul elementelor urmatoarelor sisteme si mecanisme: mecanismul biela-manivela, mecanismul de distributie a gazelor, instalatia de ungere, instalatia de alimentare cu combustibil, instalatia de racire, si sa se specifice materialele si tehnologiile de obtinere a semifabricatului.

1 Marimi si indici caracteristici

a)     Punct mort superior ( p.m.s.) este pozitia extrema a pistonului corespunzatoare volumului minim ocupat de gaze (V_c) sau pozitia pistonului corespunzatoare distantei maxime dintre acesta si axa de rotatie a arborelui cotit ( 1+r ), pozitie pentru care a si b

b)     Punct mort inferior (p.m.i.) este pozitia extrema a pistonului corespunzatoare volumului maxim ocupat de gaze (V_a) sau pozitia pistonului corespunzatoare distantei minime dintre acesta si axa de rotatie a arborelui cotit ( 1-r ), pozitie pentru care a si b

c)     Cursa pistonului (S) este spatiul parcurs de piston intre cele doua puncte moarte.

S = 2 r = 125, 24 mm (dat prin tema de proiect)

d)     Alezajul (D) reprezinta diametrul interior al cilindrului

D =101 mm dat prin tema de proiect)

e)     raportul cursa - alezaj (y) este un parametru consecutiv al motoarelor ce se exprima prin relatia :

y = S / D = 1, 24

f)      Cilindreea unitara ( V_s) reprezinta volumul generat de piston intre cele doua puncte moarte, pe cursa S:

V_s = p x D² x S = 1001, 4 cm³

g)     Cilindeea totala (V_t) reprezinta suma cilindreelor unitare ale tuturor cilindrilor

V_t = V_s x i = 6008, 88 cm³

h)     Volumul camerei de ardere ( Vc) reprezinta volumul minim ocupat de fluidul motor, cand pistonul se gaseste la p.m.s.

V_c = V_s / ( e - 1) =62, 58 cm³

unde :

e - raportul de comprimare

i)      Volumul cilindrului (V_a) reprezinta volumul maxim ocupat de fluidul motor cand pistonul se gaseste la p.m.i.

V_a = V_s + V_c = 1063, 98 cm³

j)      Raportul de comprimare (e) reprezinta raportul dintre volumul maxim ocupat de fluidul motor, cand pistonul se gaseste la p.m.i. si volumul minim ocupat de acesta, cand pistonul se gaseste la p.m.s.

e = V_a / V_c = 17 (dat prin tema de proiect).

k)     Unghiul de rotatie al arborelui cotit (a ) reprezinta unghiul facut de manivela cu axa cilindrului. Originea unghiului a a ) se alege corespunzator pozitiei pistonului in p.m.s. O cursa completa a pistonului corespunde la un unghi a RAC, iar pentru a RAC arborele cotit efectueaza o rotatie completa in timp ce pistonul parcurge doua curse simple.

l)      Viteza unghiulara a arborelui cotit (w) este acea viteza cu care arborele cotit efectueaza o rotatie completa [ 2 p rad ].

w p x n_P)/ 30 =219, 91 rad/s

m)   Viteza medie a pistonului:

w_p = S x n / 30 =8, 75 m/s

n)     Ciclul motor reprezinta succesiunea proceselor ( A,C,D,E) care se repeta periodic in cilindrii motorului.

o)     Timpul motor ( n ) reprezinta partea din ciclul motor care se efectueaza intr-o cursa simpla a pistonului

n

p)     Numarul de cicluri (Nc) reprezinta numarul grupajelor de procese ( A,C,D,E) care se repeta periodic in cilindrii unui motor, in unitatea de timp.

N_c = n / ( 30 x n

r)      Timpul de ciclu ( tc ) reprezinta timpul masurat in secunde, minute sau ore in care se desfasoara un ciclu.

t_c = 1/ N_c = 0, 05

s)     Raportul dintre raza manivelei si lungimea bielei (L) este un parametru constructiv al motorului. Pentru motoarele de autoturism L = 1/31/3,8, iar pentru motoarele de autocamion L

L

t) Lungimea bielei este:

l_b = S + 0,5. d_fm + H_bo + 1 [mm]

relatie in care:

d_fm este diametrul fusului maneton, care se calculeaza cu relatia:

d_fm = 0,61.D

adica:

d_fm = 61, 61 mm

Se adopta valoarea de 62 mm.

H_bo reprezinta inaltimea de dispunere a boltului.

H_bo = H_p - H_c

unde:

H_p este inaltimea pistonului:

H_p = 0,95.D =95, 95 mm;

H_c este inaltimea de compresie:

H_c = 0,6. H_p = 57, 57 mm.

Inlocuind, obtinem:

H_bo = 38, 38 mm,

resectiv:

l_b =195, 42 mm

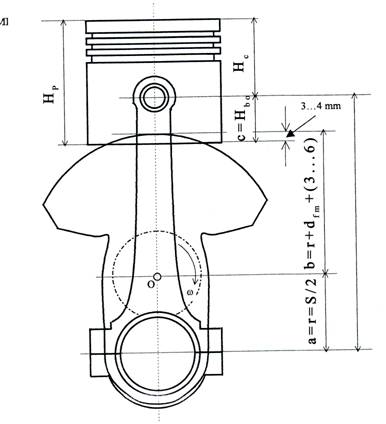
Fig. 1 Stabilirea lungimii bielei

Se adopta valoarea de 195 mm.   

2 CALCULUL INDICILOR DE PERFECTIUNE AI MOTORULUI

Presiunea indicata este raportul dintre lucrul mecanic indicat raportat la cilindreea unitara:

p_i = p_e/h_m = 8,26 MPa

Randamentul mecanic al motorului este: h_m

Cunoscand valoarea presiunii indicate se poate determina puterea indicata a motorului cu relatia :

P_i = P_e/h_m = 198, 75 kW

2.1 Calculul indicilor efectivi

Marimile efective se calculeaza cu relatiile de mai jos:

Presiunea medie efectiva

p_e = h_m x p_i= 8, 8 kW (data prin tema de proiect)

Puterea efectiva

P_e = h_m x P_i=159 kW (data prin tema de proiect)

2.2 Calculul indicilor de perfectiune

Acest calcul presupune determinarea puterii litrice (P_L), a puterii pe cilindru (P_e1) si a puterii raportate la aria cilindrului (P_A).

Pentru acestea se utilizeaza urmatoarele relatii:

Puterea litrica

P_L = P_e / V_t = 26, 46 kW/l

Puterea pe cilindru

P_e1 = P_e / i =26, 5 kW

Puterea raportata la aria pistonului

P_A = P_e1 / p x D² )/ 4 = 33, 07 kW/dm²

3. CINEMATICA MECANISMULUI MOTOR

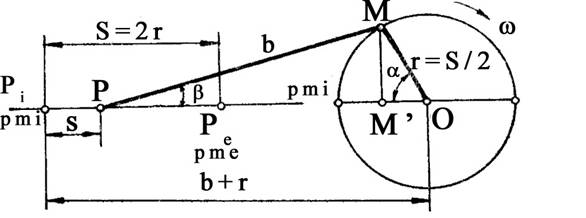
3.1 Cinematica pistonului

a) Deplasarea pistonului

Expresia deplasarii momentane a pistonului (x_p), fig.2, fata de p.m.i.este data de relatia:

x_p = r x ( 1- cos a L / 4 ) x ( 1 - cos 2 a mm

unde: r - raza manivelei

L - raportul dintre raza manivelei si lungimea bielei

Fig. 2 Determinarea cinematicii pistonului

Deplasarea pistonului poate fi considerata ca suma a doua functii armonice, astfel:

x_p = x_pI +x_pII

unde: x_pI = r x ( 1- cosa) - armonica de ordinul I

x_pII = (L / 4) x ( 1 - cos 2a) - armonica de ordinul II

Graficul de variatie a deplasarii pistonului se obtine prin puncte insumand cele doua armonici.

b) Viteza pistonului

Viteza momentana a pistonului este data de relatia :

W_p = r x w x .x sin a L / 2) sin 2a m/s

unde: w - viteza unghiulara a arborelui cotit

Si aceasta expresie poate fi considerata ca o suma a doua functii armonice, dupa cum urmeaza:

W_p = W_pI +W_pII

Unde: W_pI - r x w x x. sina - armonica de ordinul I

W_pII - r x w x x. ( L / 2).sin 2a - armonica de ordinul II

Viteza pistonului este 0 in punctele moarte. Pentru a obtine viteza maxima se anuleaza derivata functiei W_p, adica:

dW_p / da cosa L( 2 x cos² a , rezulta o ecuatie de gradul II in cosa a carei solutie da punctele de viteza maxima a_wpmax

cosa (1 -8 x L L

Pentru L = 0, 32 , avem a_wpmax

Viteza este maxima pentru aproximativ acea valoare a lui a a a_L r) la care biela este perpendiculara pe manivela.

Ea se poate calcula cu aproximatie functie de viteza medie a pistonului, cu relatia:

W_pmax = 1,625 x W_p = 14, 21 m/s

unde:

W_p = S. n/30 =8, 75 m/s

W_p fiind viteza medie a pistonului

c) Acceleratia pistonului

Acceleratia momentana a pistonului este data de relatia:

a_p = r x w x ( cosa L x cos 2a m/s

unde: r - raza manivelei

w - viteza unghiulara a arborelui cotit

Expresia acceleratiei pistonului poate fi si ea considerata ca o suma de doua functii armonice:

a_p = a_pI + a_pII

unde: a_pI = r x (w x w) cosa - armonica de ordinul I

a_pII = r x (w x w) x L cos 2a - armonica de ordinul II

Valorile extreme ale acceleratiei, in punctele moarte (a si a ) sunt date de relatiile :

a_pa = r x (w x w) x (1 + L m/s²

a_pa = r x (w x w) x (-1 + L m/s²

Cinematica bielei

Cinematica bielei se studiaza tinand seama de faptul ca biela are o miscare in plan paralel complexa. Se poate considera ca fiecare punct al bielei are o miscare de translatie identica cu a punctului P (fig.3.2) si o miscare de rotatie in jurul punctului P cu o viteza unghiulara db / dt si o acceleratie unghiulara d2b / dt2 .

a) Spatiul unghiular al bielei

Expresia spatiului unghiular este:

b = arc sin ( L x sin a

Valoarea maxima a oblicitatii bielei (b_max) se obtine pentru valoarea maxima a functiei sin a, adica la a respectiv la a , astfel incat:

b_max arc sin L = arc sin 1/

b) Viteza unghiulara a bielei

Viteza corespunzatoare miscarii bielei in jurul punctului p, va fi precizata de derivata in raport cu timpul, a functiei care exprima valoarea unghiului b

w_b L x w x cos a L x sin a rad/s

unde: w - viteza unghiulara a arborelui cotit. Viteza unghiulara a bielei inregistreaza valoarea maxima in punctele moarte (a si a ), iar pentru un mecanism normal si axat, viteza unghiulara maxima a bielei este:

w_bmax L x w

Fig. 3 Schema fortelor din mecanismul biela-manivela

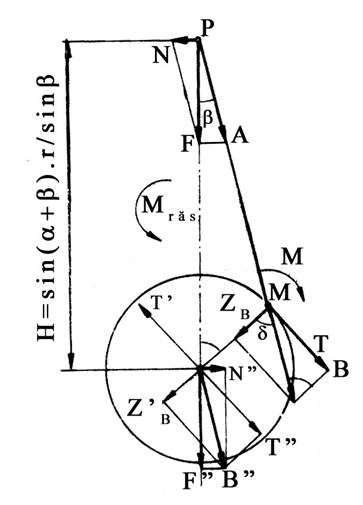
c) Acceleratia unghiulara a bielei

Acceleratia unghiulara a bielei se determina prin derivarea in raport cu timpul, a vitezei unghiulare :

e_b L x w x L - 1) x sin a L x sin a rad/s2

Calculul marimilor din cinematica mecanismului motor se face tabelar.

4. DINAMICA MECANISMULUI MOTOR

4.1 Generalitati: clasificari ale fortelor din mecanismul motor

Dinamica mecanismului motor urmareste determinarea fortelor si momentelor ce actioneaza asupra pieselor mecanismului.. Cunoasterea valorilor acestor forte si momente, precum si modul in care ele variaza, in functie de pozitia mecanismului este strict necesara pentru aflarea calculelor de rezistenta, pentru stabilirea solutiilor de echilibrare si amplasare a acestuia pe sasiu, pentru calculul variatiilor momentului motor si dimensionarea volanului, pentru stabilirea vibratiilor de torsiune a liniei de arbori, actionate de motor si a vibratiilor motorului si structurii pe care acesta este montat.

Fortele care actioneaza in mecanismul motor pot fi impartite in mai multe categorii in functie de fenomenul fizic care le produce:

a) fortele de presiune (F_p), produse de presiunea gazelor ce evolueaza in cilindrii motorului;

b) fortele de inertie ( F_j si F_r), datorate miscarii accelerate a maselor alcatuiesc mecanismul si fortele ce se transmit intre aceste piese;

c) fortele de frecare (F_f), datorita miscarii relative a pieselor ce alcatuiesc mecanismul si fortele de greutate (F_g) datorate maselor pieselor ce alcatuiesc mecanismul si fortele ce se transmit intre aceste piese.

Fortele de frecare si cele de greutate au valori mult mai mici decat celelalte doua categorii. Ca urmare, pentru calculele de interes practic, prezinta importanta doar fortele de presiune si fortele de inertie.

4.2 Forta de presiune a gazelor

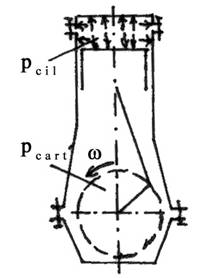
Conform principiului lui Pascal, presiunea existenta in interiorul cilindrului se exercita uniform pe toate suprafetele ( fig.4). Presiunile ce se exercita pe suprafata laterala a cilindrului si cea a camerei de ardere practicata in chiuloasa produc tensiuni si forte ce solicita mecanic cilindrul si, respectiv structura chiuloasa - bloc - carter.

Fig.4 Fortele de presiune

Presiunea exercitata pe suprafata capului pistonului determina o forta de presiune data de relatia :

F_p = π x D²/ 4 x ( p_cil - p_cart), [N]

unde: p_cil - presiunea gazelor din cilindru

p_cart - presiunea gazelor din carter

Forta de presiune a gazelor aplicata asupra cilindrului produce un lucru mecanic permitand transformarea energiei termice a fluidului motor in energie mecanica. Ea are o alura de variatie de timp, proportionala cu cea a fluidului motor.

Directia acestei forte este intotdeauna paralela cu directia axei cilindrului; cand F_p > 0 ea este orientata spre axa de rotatie a arborelui cotit, iar cand F_p < 0 ea este orientata spre chiuloasa.

4.3 Fortele de inertie

In conformitate cu principiile mecanicii newtoniene un element de masa dm, care se misca cu acceleratia a, determina o forta de inertie elementara data de relatia:

d_f = -d_m x a, [N]

Cum toate piesele mecanismului motor executa miscari accelerate, rezulta ca fiecare piesa actioneaza in cadrul mecanismului cu o forta de inertie ce poate fi calculata pe baza relatiei de mai sus.

Piesele mecanismului motor se impart in trei grupe:

grupul piston ( piston - bolt - segmenti) care executa o miscare de translatie accelerata

grupul bielei ( biela - capac - suruburi - cuzineti de biela ) care excuta o miscare plan paralela complexa

arborele cotit care executa o miscare de rotatie

Fortele de inertie care actioneaza in mecanismul motor sunt grupate in doua clase.

a)     fortele de inertie ale maselor mj care au o miscare de translatie sau o miscare alternativa, notate prescurtat Fj;

b)     fortele de inertie ale maselor mr care au o miscare de rotatie, notate prescurtat cu Fr.

a) Fortele de inertie ale maselor in miscare de translatie

Masa m_j care executa o miscare de translatie accelerata este:

m_j = m_gp + m₁ = 2, 14 kg

unde: m_gp - masa grupului piston considerata in axa boltului

m₁ - masa m1 a bielei concentrata in piciorul bielei

m_gp = m_p +m_b + m_seg =1, 64 kg

unde: m_p - masa pistonului

m_b - masa boltului

m_seg - masa segmentilor

Masa pistonului se determina cu relatia:

m_p = ρ_p x D³ = 0, 66 kg

unde: ρ_p - densitatea aparenta a pistonului fara segmenti si bolt. Pentru MAC ρ_p = 0,5 . 0,8 kg/dm³

Masa boltului se poate calcula cu relatia:

m_b = V_b x ρ_Ol =0, 18 kg

unde: V_b - volumul boltului

ρ_ol - densitatea otelului

ρ_ol = 7,6..7,8 kg/dm3

V_b = (π x L/4) x (d_eb²-d_ib²) = 0, 02 dm³

unde: L -lungimea boltului

d_eb - diametrul exterior al boltului

d_ib - diametrul interior al boltului

Masa segmentilor se adopta constructiv. Astfel, pentru motoarele cu alezajul D = 60.90 mm, masa segmentilor m_seg = 2060 g; pentru motoarele cu D = 90150 mm, masa segmentilor m_seg = 60150 g.

Pentru motorul de proiectat care are alezajul D =101 mm, adopt m_seg= 80 g

Masa bielei se descompune in doua mase ( fig. 5):

masa m1 este partea din masa bielei (m_B), care se considera ca efectueaza miscare de translatie si este concentrata in piciorul bielei;

masa m₂ concentrata in masa fusului maneton si care executa miscare de rotatie

Pentru ca efectele fortelor de inertie ale celor doua mase sa fie identice cu cele ale masei m_B a bielei, descompunerea se face respectand urmatoarele conditii:

suma celor doua mase sa fie egala cu masa bielei

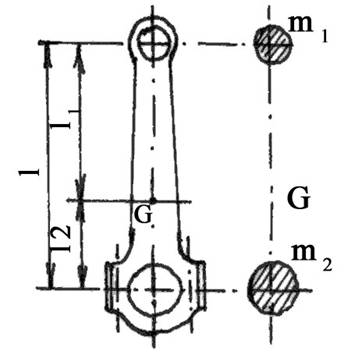
momentele statice ale celor doua mase sa fie egale

Fig.5 Descompunerea masei bielei

Masa raportata a bielei se adopta astfel: Pentru MAC cu D = 80125 mm,

m_B* = 2240 gf/cm², iar pentru MAC cu D = 60100 mm, m_B* = 2240 g/cm²,

Adopt valoarea: m_B*= 31 g/cm²

Cunoscand expresia aceeleratiei pistonului in miscare de translatie se poate calcula forta de inertie Fj, cu relatia:

F_j = - m_j x a_p,    [N]

unde: a_p - acceleratia pistonului

b) Fortele de inertie ale maselor in miscare de rotatie (Fr)

La motoarele cu cilindrii in linie, cu coturi individuale, masa totala aflata in miscare de rotatie, pentru un singur cilindru, care da nastere la forta de inertie este formata din masa neechilibrata a unui cot (m_K) si partea m₂ din masa bielei:

m_r = m_K +m₂ =22, 4 kg

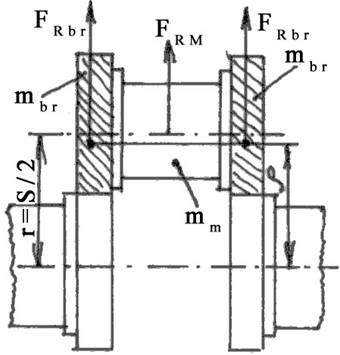
Masa neechilibrata a uniu cot se compune din (fig. 6):

Fig.6 Fortele de inertie ale maselor in miscare de rotatie

m_K = m_M + 2m_br =18, 4 kg

unde: m_M - masa fusului maneton

m_br - masa bratului

m_M = (π d_M² / 4) x l_M x ρ = 3, 80 kg

unde: d_M - diametrul fusului maneton

d_M = (0,55 . 0,75) x D

l_M - lungimea fusului maneton

l_M = (0,45 . 0,56) x d_M

ρ = densitatea otelului

ρ = 7800 . 7900 kg/m³

d_m =55, 55 mm. Adopt valoarea d_m = 56 mm

l_M =51, 001 mm Adopt valoarea l_M =51 mm

m_br = 4,85 pentru motoare de autoturism si m_br = 7,30 pentru motoare de autocamion.

m₂ = 4 kg

In concluzie se poate scrie:

F_r = F_RM +F_Rbr + F_RB

unde : F_RM - forta de inertie a masei manetonului

F_Rbr - forta de inertie a masei neechilibrate a bratului

F_RB - forta de inertie a masei m₂ a bielei

F_RM = m_Mr x ω²

F_rbr = m_br x ρ x ω²

F_RB = m² x r x ω²

4.4 Fortele rezultante din mecanismul motor

Intrucat forta de presiune a gazelor F_p si forta de inertie F_j actioneaza ambele dupa directii paralele cu axa cilindrului, ele se pot insuma algebric, dand rezultanta :

F = F_p + F_j, [N]

Forta F se descompune in doua componente si anume:

a)     o componenta N, normala pe axa cilindrului,

N = F x tg β, [N]

b)     o componenta B, de-a lungul axei bielei,

B = F / cos β, [N]

Forta N aplica pistonul pe cilindru si da nastere fortei de frecare F_f, dintre piston si cilindru, care produce uzarea celor doua organe. Tinand seama ca:

sinβ =Λ sinα,

se obtine:

tgβ = sinβ / cosβ = Λ x sinα /(1-(Λ²) x sinα²

Pentru α = 90˚se obtine:

tgβ = Λ / (1-(Λ²) sau (tgβ)_max ≈ Λ

ceea ce arata ca forta normala maxima este cu atat mai mare cu cat biela este mai scurta (Λ mai mare).

Fortele ce actioneaza asupra fusului maneton si fusului palier se determina deplasand forta B, ca vector alunecator in centru fusului maneton

(punctul M) si descompunand-o dupa doua directii : una normala la maneton, forta Z, si cealalta tangentiala la maneton, forta T:

Z = F x [cos(α + β] / cosβ, [N]

T = F x [sin(α + β] / cosβ, [N]

Avand determinata expresia fortei tangentiale T, relatia de determinare a momentului motor al monocilindrului este:

M = T. r [N.m]

unde: r - raza manivelei

Calculul fortelor rezultante din mecanismul motor se face tabelar.

5. MOMENTUL MOTOR SI PUTEREA INDICATA

5.1 Alegerea configuratiei arborelui cotit

La motorul de proiectat care are 6 cilindrii in linie, decalajul unghiular intre doua aprinderi succesive este:

Δ = 720 / i =120 ^o RAC

Rezulta ca manivelele se decaleaza intre ele cu 120 ˚, deci se afla toate in acelasi plan .

La motoarele cu patru cilindrii in linie si cu aprinderi uniform decalate, manivelele sunt doua cate doua in faza.

Tinand cont de conditia de mai sus, aleg un arbore cotit cu plan central de simetrie la care manivelele in faza sunt asezate la egala distanta de mijlocul lui (fig.7)

Fig. 7 Arbore cotit cu plan central de simetrie

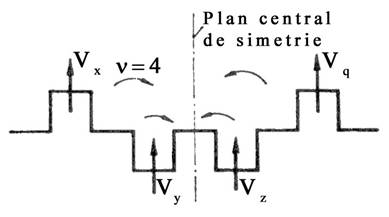Sunt posibile mai multe scheme de arbore cotit dintre care insa nu pot fi retinute decat doua, respectiv cele care prezinta plan central de simetrie. Aceste solutii sunt identice din punct de vedere dinamic, pentru ca, rotind arborele b in sens invers fata de sensul de rotatie al arborelui a, se obtine aceeasi succesiune de manivele in faza . Se zice ca cele doua solutii de arbore sunt simetrice; ele pot fi socotite ca fiind una imaginea in oglinda a celeilalte, de aceea se numesc solutii simetrice in oglinda.

Dintre cele doua solutii se alege una singura, spre exemplu solutia a, pentru care se stabilesc ordinile de aprindere posibile, repetand procesul prezentat la motorul cu 4 cilindri.

Asadar, la motorul in 4 timpi cu 6 cilindri, sunt posibile doua ordini de aprindere :

Exista mai multe criterii de triere a ordinilor de aprindere:

incarcarea minima a lagarelui arborelui cotit

reducerea pericolului de rezonanta la vibratiile de torsiune

sporirea gradului de umplere a cilindrilor

reducerea trepidatiilor motorului sub actiunea momentului de rasturnare.

Adopt ca ordine de aprindere varianta 2, 3

5.2 Determinarea tuturor ordinilor de aprindere posibile si alegerea uneia dintre acestea

Numerotarea cilindrilor este standardizata in conformitate cu STAS 8697 - 85;

Incepe dinspre flansa de cuplare a arborelui cotit cu arborele de antrenare al consumatorului.

Pentru determinarea unghiurilor de inceput al ciclului, raportate la cilindrul 1 in cazul aprinderilor uniform repartizate, se poate utiliza relatia :

α_x = 720˚ - n x δ

unde: x - numarul curent al cilindrului

n - numarul de aprinderi existente intre cea din cilinrul 1 si cilindrul x considerat:

δ - decalajul unghiular dintre doua aprinderi succesive:

δ = π x υ / i = 2, 09 ^o

5.3 Stabilirea ordinii de lucru a cilindrilor

Cilindrul 1, pornind de la α =0˚, incepe ciclul cu timpul I, respectiv admisia A. Dupa o rotire a arborelui cotit cu 360˚, manivela acestui cilindru ajunge la sfarsitul timpului II, comprimarea ( C ), cand se admite declansarea injectiei. Urmeaza timpii III si IV respectiv destinderea ( D ) si evacuarea ( E ). Conform ordinii de aprindere retinute ( 1 - 2 - 4 - 3 ), urmatoarea injectie are loc in cilindrul 2, cu un decalaj de 180˚ fata de cea din cilindrul 1, respectiv, atunci cand manivela cilindrului 2 ajunge in pozitia de p.m.i., la sfarsitul comprimarii. Evident, dupa aceasta are loc destinderea, iar apoi evacuarea si admisia. In continuare are loc injectia in cilindrul 4, decalata fata de cea din cilindrul 2 cu 180˚. Dupa injectie are loc succesiunea logica a celor patru timpi ai motorului ( D-E-A-C). Dupa injectia din cilindrul 4, cu un acelasi decalaj de 180˚, are loc injectia din cilindrul 3.

5.4 Calculul momentului motor sumar si puterii indicate

Se numeste moment motor instantaneu al unui motor monocilindric, momentul produs de forta tangenta la maneton ( T ).

Momentul M care roteste arborele cotit, produce asupra motorului un moment de reactiune care tinde sa rastoarne motorul.

Momentul motor instantaneu rezultant M, poate fi obtinut prin insumarea in intervalul d a tuturor valorilor momentului motor al monocilindrului decalate in raport cu ordinea de aprindere. Asadar, in cazul aprinderilor uniform decalate, perioada momentului motor instantaneu al unui policilindru este:

fM = fC / I = d

Este deci suficient sa se utilizeze doar varianta momentului motor al unui cilindru ( de exemplu al cilindrului 1) si sa se insumeze perioada :

fC / I = d , aceste valori decalate corespunzator.

Pentru a utiliza valorile obtinute si la calculul de rezistenta al arborelui cotit, insumarea se face pornind de la ventilator spre flansa de cuplare cu ambreiajul pe un interval de 720 din 15 in 15 RAC

Momentul mediu al motorului policilindric, se calculeaza cu relatia:

MS SMS) / n,

unde: SMS - suma valorilor momentului motor instantaneu pe o perioada.

d fC / I = 120 RAC

Garficul variatiei momentului sumar pentru o perioada de 120 si momentul motor este redat la anexa.

6 CALCULUL CAMASII CILINDRULUI

6.1 Stabilirea dimensiunilor principale ale camasilor:

Dimensiunile cilindrilor (figura 8) se stabilesc cu ajutorul relatiilor urmatoare:

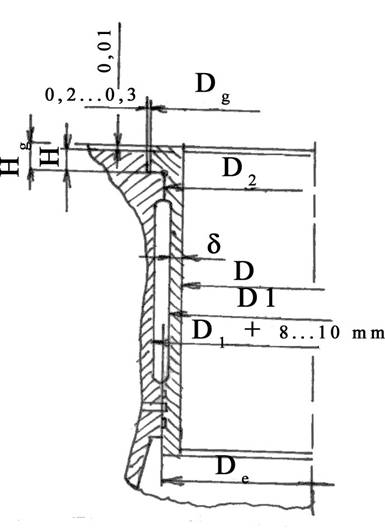
Fig. 8 Dimensiunile camasii cilindrului

Lungimea camasii cilindrului ( L_c )

L_c = S + L - b

unde: S - cursa pistonului

L - lungimea pistonului; Adopt: L = D x (0,8..1,1) = 90, 9 mm

b - 1015 mm; Adopt b = 12 mm

L_c =201, 14 mm

Lungimea camerei de racire ( L_cr)

L_cr = S + 2a

Lungimea camerei de racire trebuie aleasa astfel incat sa depaseasca primul segment de compresie cand pistonul se afli la p.m.i. si la p.m.e.

cu a = 6.10 mm

Adopt a = 8 mm

L_cr =141, 24 mm Adopt L_cr =142 mm

Grosimea peretilor ( σ )

σ = 0,05 x D + 2 = 6, 54 mm Adopt : σ =7 mm

Diametrul exterior al gulerului de sprijin ( D_g )

Diametrul exterior al gulerului de sprijin se determina din conditia ca presiunea ( p_c) care ia nastere la suprafata de contact (A) dintre guler si bloc sa nu depaseasca presiunea admisibila a materialului blocului ( pentru Fc = 250, p_a = 420 Mpa)

p_c = F / A < p_a

unde: F - forta care apasa asupra gulerului datorita stangerii chiuloasei

Aceasta forta trebuie sa fie de 1,3 ori mai mare decat forta data de presiunea maxima ( p_{cil max}) din cilindru, adica:

F = 1,3 p_cil x (π x D² / 4 )

Aria de contact cu chiuloasa este data de relatia :

A = [ π (Dg² - D² )] / 4

Din relatiile anterioare se obtine expresia diametrului exterior la gulerului :

D_g = [1,3 x D² ( p_i / p_a) + D² ]^1/2

D_g = (64557, 11)^1/2 = 254, 08 mm

Adopt : D_g = 254 mm

Diametrul gulerului se va lua mai mare sau cel putin egal.

Inaltimea minima a gulerului ( H_g )

Se va determina din conditia de rezistenta la incovoiere. Sarcina q uniform distribuita pe suprafata de contact se detremina din conditia :

F = q (π x D_g² x Dg ) - D) / 4

deci : q = 4x F / D_g ²- D²

Momentul incovoietor maxim este :

M_max = q ( D_g -D_g²) / 2

Modulul de rezistenta axial se calculeaza cu expresia:

Wz = l x H_g / 6

Din conditia ca tensiunea maxima de incovoiere sa fie cel mult egala cu tensiunea admisibila (σa) rezulta:

σ_i = M_max / W_z = σ_a

Tensiunea admisibila se determina in raport cu tensiunea de rupere:

σ_r = 280 Mpa

iar : σ_a = σ_r / C_r

unde: C_r - coeficient de siguranta la rupere (C_r = 3)

F = 1,3 x p_cil (3,14 x D²)/4 = 206, 7 N

q = 0, 012 N/m²

Momentul incovoietor maxim este :

M_max = q ( D_g - D²)² / 2

M_max =593, 56 N.m

Tensiunea admisibila este:

σ_a = σ_r / C_r

σ_r = 280 Mpa

σa =93, 33 Mpa

Inaltimea gulerului este :

H_g = (6 x M_max / σ)^1/2

Se adopta valoarea : H_g =22, 55 mm

Pentru alegerea dimensiunilor inelelor de cauciuc si santurilor corespunzatoare am adoptat urmatoarele valori:

D_i = D² + ( 0,5..1) mm Adopt : D_i = 13, 31 mm

d = 4 mm

t = 3,5 mm

e = 2 mm

a = 8 mm

b = 6 mm

c = 4 mm

6.3 Calculul de rezistenta pentru solutia adoptata

Calculul de rezistenta al camasii cilindrului consta in verificarea grosimii (δ) a peretelui. Calculul se bazeaza pe teoria tuburilor cu pereti grosi.

Camasa cilindrului este solicitata de:

presiunea gazelor de ardere ( p_cil)

forta normala N transmisa de piston

presiunea ce ia nastere pe suprafata de contact cu blocul

tensiunile ce iau nastere datorita incalzirii inegale

a)     Determinarea tensiunilor datorate presiunii gazelor

Aceste tensiuni se determina cu expresiile :

σ_α,r = R² x p_cil / (R₁² - R²)

Pe conturul interior r = R₁ = 42, 91 mm

σ_ri = p_cil

σ_αi = ( R_l² + R² ) / ( R_l² - R² ) x p_cil

σ_αi =24, 51 MPa

Pe conturul exterior r = R₁ = 45 mm

σ_re = 0

σ_αe = [2 x R² /( R₁² - R²)] x p_cil

σ_αi =20, 93 Mpa

b)     Calculul tensiunilor termice

Tensiunile principale care apar in peretii camasii de cilindru au expresiile :

σ_r = E x α. ( t_i - t_e)/ 3. ( 1-ν )( R₁ - R)[r -(R₁³-r³) / (R₁² -R²) + r² X r₁² / ( r + r₁)X R²)] = 0

σ_α = E x α₀( t_i - t_e)/ 3( 1-ν )( R₁ - R)[(R₁³-r³) / (R₁² -R²) - R² X R₁² / ( R + R₁)X r²)]

unde : E - modulul de elasticitate longitudinal ( pentru fonta E = 1,21,6 x 10⁵ Mpa

Adopt : E = 1,4 x 10⁵ MPa

α₀ = coeficient de dilatare termica liniara ( pentru fonta : α₀ = 10^-5 grd ^{- 1}

ν = coeficient al contractiei transversale

t_i, t_e = temperaturile in interiorul si exteriorul camasii

Adopt : t_i = 140^oC; t_e = 80^oC

r = o raza oarecare

7. CALCULUL PISTONULUI

Calculul dimensiunilor caracteristice

Dimensiunile principale ale pistonului se adopta dupa date statistice rezultate din studiul solutiilor de motoare similare dupa cum urmeaza :

D =101 mm

L = (0,8 . 1) x D =90, 9 mm

H_c = (5,5 . 0,7) x D = 60, 6mm

L_m = (0,5 . 0,8) x D =70. 7 mm

d . 0,1) x D = 8, 08 mm

H₁ = (0,06 . 0,12) x D = 10, 1 mm

H = 2,5 mm

H₂ = (0,035 . 0,045) x D = 4, 04 mm

B = (0,3 . 0,4) x L = 27, 27 mm

L' = 0,52 x L = 42, 26 mm

A = (0,042 . 0,052) x D = 4, 24 mm

8. CALCULUL BOLTULUI

Fig. 9 Dimensiunile boltului

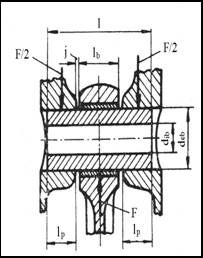
d_eb = (0,24 . 0,28) x D = 26, 26 mm

Adopt : d_eb =26 mm

d_ib = (0,65 . 0,75) x d_eb =18, 90 mm

Adopt d_ib =19 mm

l = (0,88 . 0,93) x D =90, 9 mm

Adopt l = 90 mm

j = 0,05 mm

l_b = (0,26 . 0,3) x D = 29, 29 mm

Adopt l_b =29 mm

9. CALCULUL ARBORELUI COTIT

Calculul dimensiunilor principale:

Lungimea cotului

l = (1,1 . 1,25) x D = 121, 12 mm

Diametrul fusului palier

d_p = (0,6 . 0,8) x D = 70, 7 mm

Lungimea fusului palier intermediar

l_pi = (0,45 . 0,6) x d_p =30, 3 mm

Lungimea fusului palier de capat segment central

l_pi = (0,74 . 0,84) x d_p =44, 84 mm

Diametrul fusului maneton

d_M = (0,45 . 0,65) x D =45, 45 mm

Lungimea fusului maneton

l_M = (0,45 . 0,65) x d_M = 24, 99mm

Diametrul orificiului longitudinal din fusul maneton

d_Mi = (0,6 . 0,7) x d_M =33, 33 mm

Grosimea bratului

h = (0,2 . 0,25) x D =22, 22 mm

Latimea bratului

b = (1 . 1,25) x D = 112, 11 mm

Raza de racordare

j = (0,06 . 0,1) x d_M = 8, 08 mm

10. CALCULUL MECANISMULUI DE DISTRIBUTIE

Alegerea dimensiunilor supapelor

-Diametrul mare al taletului ds:

-pentru SA: 8 mm - ds

-pentru SE: 10 mm - ds

-Diametrul mic al talerului ds*:

ds* = d_o = 0,865. ds

-pentru SA: d_o = 0,865. ds_SA =6, 53 mm

-pentru SE: d_o = 0,865. ds_SE = 8, 49 mm

-pentru SA: ds* = 1,0. d_o mm

-pentru SE: ds* = 1,0. d_o = 37, 77 mm

-Raza de racordare a talerului "r_t".

r_tSA = 0,30. d_oSA =1, 95 mm

r_tSE = 0,30. d_oSE = 2, 54mm

-Diametrul tijei:

-pentru SA: d =13, 64 mm

-pentru SE: d = 17, 74 mm

-Lungimea sediului b:

b_SA = 0,12. d_oSA = 0, 78 mm

b_SE = 0,12. d_oSE =1, 01 mm

-Lungimea supapei "l"

-pentru SA: l_SA =116, 67 mm

-pentru SE: l_SE =117,08 mm

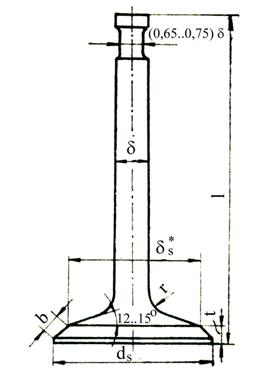
Fig 9 Dimensiunile supapei

-Inaltimea cilindrica a talerului "t₁"

t_1SA =0, 89 mm

t_1SE =1, 01 mm

-Inaltimea totala a talerului "t":

t_SA =3, 66 mm

t_SE =3, 77 mm

-Inaltimea maxima de ridicare "h_Smax"

h_SA =8, 10 mm

h_SE = 8, 30 mm

11. CALCULUL DE DIMENSIONARE A ELEMENTELOR INSTALATIEI DE RACIRE

a)     Calculul radiatorului

Pentru autovehiculul din tema de proiect am optat pentru un radiator din alama, deoarece este mai robust si asigura un regim termic de functionare corespunzator.

Fluxul de caldura evacuat prin radiator:

F_rac = K_rad.A_aer. Dt_m   

relatie in care:

K_rad reprezinta coeficientul global de schimb de caldura. Am optat pentru valoarea k_rad = 80 [3]

A_aer este suprafata de schimb de caldura pentru aer. Din relatia:

A_aer/P_emax = 0,25

rezulta:

A_aer = 0,25.P_emax = 39, 75

Dt_m este egal cu diferenta dintre temperatura lichidului de racire si temperatura mediului ambiant. Pentru m.a.c. Dt_m = 70 K.

Coeficientul de nervurare:

j_aer = A_aer/A_l (6.3)

unde A_l este suprafata de schimb de caldura pentru lichidul de racire.. Din [1] am optat pentru valoarea j_aer

Aria frontala a radiatorului:

A_f = F_rac F Dt_m (6.4)

relatie in care F reprezinta fluxul de caldura schimat in radiator pe unitatea de suprafata frrontala; F = 3.10³ W.

Din [1] am optat pentru valoarea A_f = 0,8 m²

Numarul de tevi ale radiatorului:

i_t = F_rac j_aer/3600.A_aer.r_aer.w_aer.c_{p aer}. . Dt_m=    

cu:

.r_aer = 1,2 kg/m³

w_aer = 38,89 m/s

c_{p aer} = 1 J/kg.K

b)    Pompa de apa

Debitul real:

V`p = h_p p.c_i.(r₁² r_o²) [m³/s] (6.6)

Se adopta [3] V`p =70 m³/s;

Latimea paletelor:

b = p.c_I .(r₁²- r_o²)( p.D₁ - d_s/sinb1).w_I    (6.7)

Se adopta [3] b = 3,5 mm;

Raza rotorului:

r = (u₂/w_p) - (30.u₂/p.n_p) (6.8)

Se adopta [3] r = 200 mm;

Puterea pompei:

P = 10^-3.V`p [kw]; Puterea pompei P = 70 w

- Presiunea de lucru: 0,4 bar

c)     Ventilatorul

Diametrul: F = 0,6m

Lungimea paletei: L = 220 mm;

Latimea paletei: l = 60 mm;

Grosimea paletei: h = 1,6 mm;

Viteza periferica a elicei: w = 90 m/s;

Viteza curelei: 20 m/s;

Numarul paletelor

3.2 CALCULUL ELEMENTELOR SISTEMULUI DE UNGERE

3.2.1 Calculul debitului de ulei

In ipoteza ca uleiul preia caldura dezvoltata prin frecare, care reprezinta fractiunea f_u din caldura degajata, adica:

Q_u = f_u. C_c. Q_i     [kJ/h]

intrucat C_c = 10^-3. c_e. P_e [kg/h]

unde c_e este in g/kWh iar P_e in kW, rezulta:

Stiind ca Q_i = 40.000 . 44.000 kJ/kg si ca c_e = 230 . 300 g/kWh, rezulta:

Q_u = (9 . 13). 10³. f_u. P_e (3.4)

Se admite [3] ca f_u = 0,02 . 0,06 si obtinem:

Q_u = (260 . 540). P_e    [kJ/h]

Adoptand valoarea spre limita inferioara [3] de 300, obtinem:

Q_u = 47700 kJ/h

Debitul de ulei care trece prin magistrala va fi:

V_u = Q_u/c_u. r_u Dt_u    (3.6)

Cu valorile mentionate anterior si tinand seama ca:

c_u. r_u = 1674 . 1883 kJ/m³K; Dt_u = 15, rezulta:

V_u = (9 . 20).P_e [l/h] (3.7)

Adoptand o valoare spre limita inferioara [3] de 12, obtinem:

V_u =1590 l/h

unde P_e este in kW. Pe baza datelor statistice s-a mai stabilit:

V_u = (6 . 13). n_P. d²_f.b [l/h] (3.8)

unde n_P este turatia de putere maxima in rot/min; d_f reprezinta diametrul fusului iar b numarul de fusuri.

Volumul de ulei din carter V_uc se determina in ipoteza ca uleiul efectueaza aproximativ 100 . 250 treceri pe ora, deci V_uc = V_u/(100 . 250)

Rezulta:

V_uc =6, 625 l

In tabelul 7 sunt prezentate valorile orientative pentru volumele de ulei [3]:

Tab. 3.1

Valori orientative pentru volumele de ulei

V_uc - debitul uleiului care circula prin rampa centrala

V_pu - debitul livrat de pompa (include si uleiul care trece prin supapa de siguranta)

3.2.2 Dimensionarea pompei de ulei

In tabelul 8 sun date valori orientative pentru dimensionarea pompelor de ulei

Tab. 3.2

Elemente pentru dimensionarea pompelor de ulei

In baza acestor date, am adoptat urmatoarele valori:

Diametrul D_p = 50 mm

Numarul de dinti z = 10

Inaltimea dintilor h = 10 mm

Modulul m = 4,5 mm

Latimea dintilor l = 46 mm

Viteza periferica a rotii dintate v = 5 m/s

Turatia pompei n_p = n/2.