	Aeronautica	Comunicatii	Constructii	Electronica	Navigatie	Pompieri
	Tehnica mecanica

Tehnica mecanica

Index » inginerie » Tehnica mecanica
» Dinamica punctului material in miscare absoluta

Dinamica punctului material in miscare absoluta

DINAMICA PUNCTULUI MATERIAL IN MISCARE ABSOLUTA

1. NOTIUNI FUNDAMENTALE

1.1. LUCRUL MECANIC

Fig. 11.1

Prin definitie, lucrul mecanic efectuat de forta la deplasarea punctului material din pozitia M₀, in pozitia M₁ este dat de integrala curbilinie:

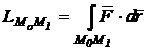(11.1)

unde este deplasarea efectuata de punctul de aplicatie al fortei in timpul elementar (fig.11.1).

Pentru o forta constanta si o deplasare rectilinie a punctului material, lucrul mecanic este:

(11.2)

Forta este in general o functie de timpul t, pozitia si viteza a punctului de aplicatie. Deplasarea , efectuata pe arc, este constituita din deplasari elementare MM’, care se pot asimila cu deplasarile pe corzile corespunzatoare (fig.11.1). In aceasta deplasare elementara, forta este admisa constanta. Lucrul mecanic al fortei pe o deplasare elementara se numeste lucrul mecanic elementar:

(11.3)

Daca in relatia (11.3) se inlocuieste , in care este viteza punctului material, se obtine:

(11.4)

Lucrul mecanic al fortei , in deplasarea finita din M₀ in M₁ este numit lucrul mecanic total sau finit si este determinat prin integrala curbilinie (11.1).

Daca vectorii sunt exprimati prin proiectiile lor pe axele unui sistem cartezian Oxyz, lucrul mecanic total are expresia:

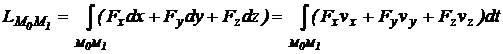(11.5)

1.2. FUNCTIA DE FORTA

Se considera o functie scalara U(x,y,z) exprimata cu coordonatele punctului, cu ajutorul careia pot fi scrise componentele fortei astfel:

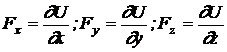(11.6)

Functia U se numeste functie de forta iar forta se numeste forta conservativa si deriva din functia de forta U.

Conditiile lui Cauchy, de existenta pentru functia U sunt:

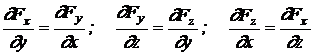(11.7)

Deci forta conservativa este:

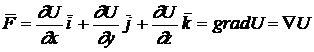(11.8)

unde operatorul (nabla), numit si operatorul Hamilton este un operator vectorial, care transforma un scalar intr-un vector.

Lucrul mecanic elementar este:

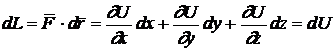(11.9)

iar lucrul mecanic total va fi:

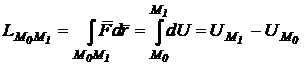(11.10)

unde:

Lucrul mecanic total al unei forte conservative este independent de traiectoria parcursa si depinde numai de pozitiile initiale si finale ale punctului.

Dintre fortele conservative, deci care formeaza campuri potentiale, amintim greutatea si forta elastica.

Greutatea are proiectiile pe axele reperului Oxyz (fig.11.2):

(11.11)

Prin urmare:

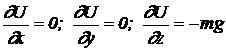(11.12)

Fig. 11.2

Conditiile lui Cauchy (11.7) sunt indeplinite si deci forta de greutate este o forta potentiala. Functia de forta pentru greutate este:

(11.13)

Lucrul mecanic total L_MoM efectuat de greutate, in deplasarea punctului din pozitia M₀, in pozitia M are expresia:

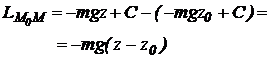(11.14)

Considerand ca suportul fortei elastice are o directe oarecare in spatiu (fig.11.3) putem scrie:

Fig. 11.3

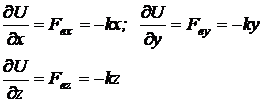(11.15)

Conditiile lui Cauchy (11.7) fiind indeplinite, forta elastica este o forta potentiala. Functia de forta pentru forta elastica este:

(11.16)

Lucrul mecanic total L_MoM efectuat de forta elastica, in deplasarea punctului din pozitia M₀, in pozitia M este:

(11.17)

1.3. PUTEREA

Prin definitie, puterea este lucrul mecanic produs in unitatea de timp:

(11.18)

cand forta si momentul (in cazul rigidului) sunt constante in timp, sau:

(11.19)

cand forta si momentul sunt variabile.

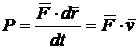(11.20)

sau considerand rotatia elementara ca vector:

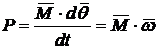(11.21)

1.4. RANDAMENTUL MECANIC

Intr-o masina fortele motoare produc lucrul mecanic motor L_m. Fortele rezistente produc lucrul mecanic util L_u, in scopul pentru care a fost construita masina si lucrul mecanic pasiv L_p, folosit pentru invingerea frecarilor.

(11.22)

Se defineste randamentul mecanic, notat cu h, raportul:

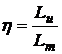(11.23)

care este o marime adimensionala si indica modul cum foloseste masina, lucrul mecanic motor.

Exprimand lucrul mecanic util in functie de cel motor si inlocuindu-l in expresia (11.23), rezulta:

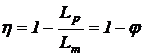(11.24)

unde se numeste coeficient de pierderi.

Se constata ca, intotdeauna

1.5. IMPULSUL

Fig. 11.4

Notiunea de impuls a fost introdusa sub forma stiintifica de Leonardo da Vinci si Galileo Galilei, numita de Newton si cantitate de miscare.

Prin definitie, impulsul unui punct material M de masa m, care se misca cu viteza este un vector coliniar cu si a carei expresie este (fig.11.4):

(11.25)

1.6. MOMENTUL CINETIC

Momentul cinetic al unui punct material M de masa m, care se misca cu viteza calculat in raport cu un punct fix O, este prin definitie momentul impulsului punctului M, calculat in raport cu acelasi punct O:

Fig. 11.5

(11.26)

Momentul cinetic se mai numeste si momentul cantitatii de miscare si este un vector legat, analog vectorului moment al unei forte in raport cu un punct, definit in statica (fig.11.5).

1.7. ENERGIA MECANICA

Energia cinetica

Pentru un punct material de masa m care are viteza , prin definitie, energia cinetica este:

(11.27)

Energia cinetica este o marime de stare, scalara si strict pozitiva (marime care caracterizeaza miscarea, in orice moment).

Energia potentiala

Energia potentiala este o marime care caracterizeaza capacitatea miscarii nemecanice de a trece intr-o anumita cantitate de miscare mecanica.

Energia potentiala se pune in evidenta cand fortele care actioneaza asupra punctului material sunt forte conservative (deriva din functii de forta U).

Daca forta conservativa admite o functie de forta U(x,y,z), functia potential sau energia potentiala reprezinta functia de forta, luata cu semnul minus.

(11.28)

Pentru lucrul mecanic elementar si total al fortei , care se deplaseaza din pozitia M₀ in pozitia M se obtin expresiile:

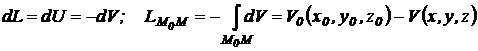(4.29)

Semnificatia functiei potential V(x,y,z) rezulta, admitand ca punctul M₀(x₀,y₀,z₀) este punct de potential zero si prin urmare, functia de forta U(x₀,y₀,z₀) respectiv, potentialul V(x₀,y₀,z₀) sunt nule. Exprimand lucrul mecanic al fortei conservative , cand punctul se deplaseaza din M in M₀, rezulta:

(11.30)

Energia potentiala a punctului material corespunzatoare pozitiei M(x,y,z) reprezinta lucrul mecanic efectuat de forta conservativa la deplasarea punctului din pozitia M in pozitia M₀, care prin conventie are potentialul nul.

Se numeste energie mecanica a punctului material actionat de o forta conservativa, suma intre energia cinetica si energia potentiala

(11.31)

2. ECUATIILE DIFERENTIALE ALE MISCARII PUNCTULUI MATERIAL

2.1. GENERALITATI

In dinamica punctului material se intalnesc doua categorii de probleme:

Problema directa Se cunosc fortele care actioneaza asupra punctului material ca natura, suport, sens, marime si se cere sa se stabileasca miscarea punctului material.

Forta este data de o expresie avand forma:

(11.32)

A cunoaste miscarea inseamna a obtine o relatie vectoriala de tipul:

(11.33)

Legea fundamentala a dinamicii este:

(11.34)

Cum acceleratia este si tinand seama de relatia (11.32) se scrie:

(11.35)

S-a obtinut astfel o ecuatie diferentiala de ordinul doi care reprezinta ecuatia diferentiala a miscarii. Aceasta ecuatie vectoriala se proiecteaza pe axe si se solutioneaza sub forma scalara

Problema inversa Se cunoaste miscarea, data de o relatia (11.33) si se cere forta care produce miscarea. Pentru aceasta se deriveaza de doua ori in raport cu timpul relatia (11.33) si se introduce in relatia fundamentala a dinamicii scrisa sub forma (11.34). Se obtine astfel ecuatia diferentiala a miscarii.

In general problema nu este univoc determinata, deoarece nu se poate stabili si natura fortei.

2.2. ECUATIILE DIFERENTIALE ALE MISCARII PUNCTULUI MATERIAL LIBER

Ecuatia diferentiala, sub forma vectoriala (11.35), proiectata pe un sistem de axe, convenabil ales conduce la urmatoarele ecuatii scalare, functie de sistemul de coordonate in care se lucreaza.

In sistemul de coordonate carteziene

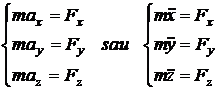(11.36)

unde reprezinta proiectiile pe axele Ox, Oy si respectiv Oz ale rezultantei fortelor care actioneaza asupra punctului material;

In sistemul de coordonate naturale (triedrul Fren t)

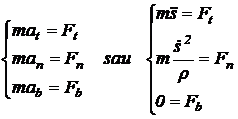(11.37)

unde reprezinta proiectiile pe axele sistemului Fren t (tangenta, normala principala si binormala) ale rezultantei fortelor care actioneaza asupra punctului material.

Integrarea ecuatiilor diferentiale ale miscarii este in general, aceeasi in toate sistemele de referinta

In continuare se vor integra ecuatiile diferentiale ale miscarii in sistemul cartezian. Ecuatiile diferentiale ale miscarii conform (11.36) vor fi:

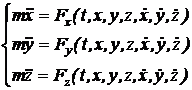(11.38)

Sistemul de ecuatii diferentiale de ordinul doi are ca necunoscute, ecuatiile parametrice ale traiectoriei:

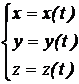(11.39)

Sistemul de ecuatii diferentiale (11.38) admite un sistem unic de solutii, deci sub actiunea unei forte date, miscarea efectuata de punct este unica. Integralele generale ale sistemului (11.38) contin sase constante arbitrare de integrare .

Integralele generale au expresia:

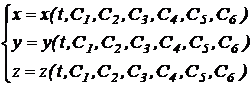(11.40)

Derivand in raport cu timpul relatiile (11.40) se obtine:

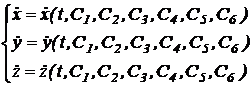(11.41)

Cu ajutorul relatiilor (11.40) si (11.41) se pot determina constantele de integrare punand conditiile initiale, la , referitoare la pozitia initiala si viteza initiala .

Astfel conditiile initiale de pozitie sunt:

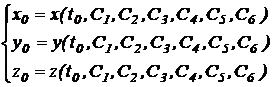(11.42)

iar conditiile initiale de viteza sunt:

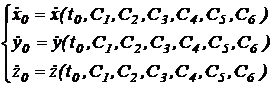(11.43)

Relatiile (11.42) si (11.43) formeaza un sistem algebric de 6 ecuatii cu 6 necunoscute . Rezolvand acest sistem se obtin valorile constantelor de integrare in functie de conditiile initiale date:

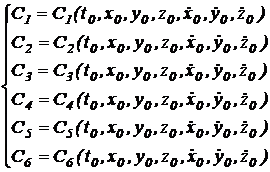(11.44)

Introducand valorile constantelor de integrare din (11.44) in (11.40) se obtin ecuatiile parametrice ale traiectoriei si introducand-le in (11.41) se obtin componentele vitezei la un moment dat. Solutia problemei este univoca

In unele cazuri, obtinerea solutiei generale pentru sistemul (11.38) nu este posibila in schimb se pot obtine integrale prime. O integrala prima este o functie de timpul t, vectorul si vectorul , care se reduce la o constanta daca reprezinta o solutie a ecuatiei diferentiale. Integrala prima reprezinta deci in general, o ecuatie diferentiala al carei ordin este mai mic cu o unitate decat ecuatia diferentiala data

Observatie. Cu ajutorul ecuatiilor diferentiale ale miscarii punctului material se poate studia si miscarea corpurilor intalnite in practica, cu conditia ca fortele care actioneaza asupra acestora sa fie concurente intr-un singur punct.

2.3. ECUATIILE DIFERENTIALE ALE MISCARII PUNCTULUI MATERIAL SUPUS LA LEGATURI

Un punct material este supus la legaturi daca i se impun anumite restrictii geometrice, respectiv sa ramana in permanenta pe o suprafata sau o curba data.

Miscarea punctului material supus la legaturi se studiaza aplicand axioma legaturilor, in baza careia punctul material se elibereaza de legaturi, introducand fortele de legatura si studiind miscarea ca si cum ar fi liber.

Notand rezultanta fortelor direct aplicate cu si a fortelor de legatura (reactiunea) cu , ecuatia de miscare a punctului material supus la legaturi este:

(11.45)

Ecuatia diferentiala, sub forma vectoriala (11.45), proiectata pe un sistem de axe, convenabil ales conduce la urmatoarele ecuatii scalare:

In sistemul de coordonate carteziene

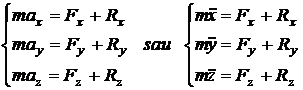(11.46)

unde si sunt proiectiile pe axele Ox, Oy, Oz ale rezultantei fortelor direct aplicate, si de legatura care actioneaza asupra punctului material.

In sistemul de coordonate naturale (triedrul Fren t)

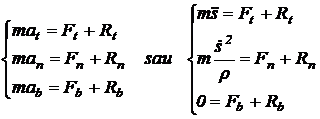(11.47)

unde si reprezinta proiectiile pe axele sistemului Fren t ale rezultantei fortelor direct aplicate si de legatura

Integrarea ecuatiilor diferentiale ale miscarii este aceeasi ca in cazul punctului material liber.

3. TEOREMELE GENERALE IN DINAMICA PUNCTULUI MATERIAL

3.1. TEOREMA IMPULSULUI

Derivata in raport cu timpul a impulsului unui punct material este egala in fiecare moment cu rezultanta fortelor care actioneaza asupra punctului.

Derivand in raport cu timpul impulsul dat de relatia (11.25) se obtine:

(11.48)

Cum in baza legii fundamentale a dinamicii (11.34), , rezulta:

(11.49)

Proiectand pe axe relatia (11.49) se obtine:

(11.50)

Conservarea impulsului

Daca in timpul miscarii punctul material este izolat sau rezultanta fortelor care actioneaza asupra acestuia este nula, atunci:

(11.51)

Deci impulsul se conserva, adica pastreaza in timp aceeasi valoare. Constanta se determina din conditiile initiale ale problemei.

Este posibil sa se conserve in timp o singura componenta a impulsului. Astfel, daca

(11.52)

In acest caz se conserva componenta impulsului dupa axa Ox.

3.2. TEOREMA MOMENTULUI CINETIC

Derivata in raport cu timpul a momentului cinetic calculat in raport cu un punct fix O, este egala cu momentul in raport cu acelasi punct al rezultantei fortelor care actioneaza asupra punctului material.

Derivand in raport cu timpul expresia momentului cinetic (11.26), rezulta

(11.53)

Cum reprezinta momentul in raport cu punctul O, al rezultantei fortelor care actioneaza asupra punctului material, rezulta teorema momentului cinetic:

(11.54)

Proiectand pe axe, relatia (11.54) se obtine:

(11.55)

Conservarea momentului cinetic

Daca in timpul miscarii, punctul material este izolat sau momentul rezultant care actioneaza asupra acestuia este nul, rezulta

(11.56)

Deci momentul cinetic se conserva, adica pastreaza aceeasi valoare in timp. Constanta se determina din conditiile initiale.

Se poate conserva o singura componenta a momentului cinetic, de exemplu:

(11.57)

In acest caz se conserva componenta momentului cinetic dupa axa Ox.

3.3. TEOREMA ENERGIEI CINETICE

Variatia energiei cinetice a punctului material in intervalul de timp dt, este egala cu lucrul mecanic elementar, efectuat de rezultanta fortelor aplicate punctului in acelasi interval de timp. (forma diferentiala

Diferentiind relatia energiei cinetice si tinand seama de legea fundamentala a mecanicii (11.34), , rezulta

Termenul din stanga reprezinta o diferentiala totala exacta, pe cand termenul din dreapta reprezinta o diferentiala de tip Pfaff, care este o diferentiala totala exacta, numai in cazul particular al fortelor conservative. Forma diferentiala a teoremei energiei cinetice este:

(11.58)

Integrand rezulta teorema energiei cinetice, forma integrala

(11.59)

Variatia energiei cinetice intre pozitia initiala si finala a miscarii punctului material este egala cu lucrul mecanic total efectuat in deplasarea finita intre cele doua pozitii, de rezultanta fortelor aplicate punctului material.