 | Aeronautica | Comunicatii | Constructii | Electronica | Navigatie | Pompieri |
| Tehnica mecanica |
CUPTORUL CU ARC ELECTRIC CA GENERATOR DE ARMONICI SI SARCINA TRIFAZATA NEECHILIBRATA
Capitolul de fata isi propune sa analizeze cuptorul trifazat cu arc electric ca o sursa de regim periodic nesinusoidal si nesimetric. In acest scop sunt prezentate mai intai marimile caracteristice semnalelor periodice nesinusoidale, apoi pe baza acestora se definesc marimile electrice specifice regimului deformant al cuptorului electric. In partea a doua a capitolului sunt analizate posibilitati de modelare a arcului electric fiind obtinute concluzii importante privitor la performantele obtinute de fiecare.
1. Regimul periodic nesinusoidal in sistemele electroenergetice
1.1. Generalitati
Sursele de regim deformant pot fi clasificate in surse de tensiuni armonice si surse de curenti armonici [1].
Analiza spectrala a undei de curent si de tensiune releva frecvente multiple ale fundamentalei de 50 Hz, denumite armonice. Domeniile de frecventa care corespund acestor armonice sunt, in general cuprinse intre 100 Hz si 2000 Hz, respectiv armonicele de rang k = 2 si a celor de rang k = 40. Este posibil insa sa existe in tensiunea retelei electrice si "interarmonici", acestea fiind componente a caror frecventa este situata intre armonicele frecventei retelei.
1. Caracteristici ale marimilor periodice nesinusoidale
Deoarece metodele de analiza analogica a caracteristicilor marimilor periodice nesinusoidale au fost inlocuite tot mai mult cu metodele numerice se va prezenta modul de utilizare a transformatei Fourier in analiza semnalelor periodice [55].
Aceasta metoda prezinta avantajul determinarii fazelor armonicilor in raport cu trecerea prin zero. Se defineste functia periodica de perioada T functia care indeplineste relatia
![]() , (1)
, (1)
T fiind perioada iar ![]() , pulsatia.
, pulsatia.
Functia periodica ![]() poate fi
reprezentata de seria Fourier
poate fi
reprezentata de seria Fourier
![]() (2)
(2)
unde
![]() (a)
(a)
si
![]() . (b)
. (b)
Coeficientii care intervin in relatiile anterioare se pot deduce potrivit relatiilor
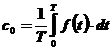 , (a)
, (a)
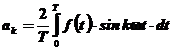 , (b)
, (b)
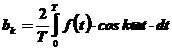 . (c)
. (c)
Amplitudinea armonicii de ordinul k se poate determina cunoscand coeficientii ak si bk potrivit relatiei
![]() . (4)
. (4)
Valoarea medie a produsului a doua armonici
![]()
si
![]()
este data de relatia
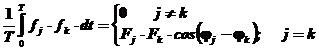 . (5)
. (5)
Valoarea efectiva a unei marimi periodice nesinusoidale este data de
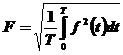 , (6)
, (6)
relatie care poate fi rescrisa sub forma
![]() . (7)
. (7)
Pentru marimi periodice alternative simetrice de forma
![]() (8)
(8)
se defineste factorul de varf sau de creasta ca raportul intre valoarea maxima si valoarea efectiva
![]() , (9)
, (9)
si factorul de forma ca raportul intre valoarea efectiva si valoarea medie a alternantei pozitive
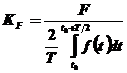 , (10)
, (10)
unde t0 este momentul in care semnalul trece prin zero cu valori crescatoare.
Criteriile de analiza cantitativa a componentei de armonici in structura unui semnal sunt [1],[55]:
a) Nivelul armonicii - reprezinta raportul exprimat in procente dintre valoarea efectiva a armonicei considerate (Fk) si valoarea efectiva a fundamentalei F1
![]() . (11)
. (11)
b) Reziduul deformant reprezinta unda care se obtine din unda data suprimandu-se armonica fundamentala
![]() . (12)
. (12)
c) Coeficientul global de distorsiune (nesinusoidalitate) se defineste ca raportul exprimat in procente dintre valoarea efectiva a reziduului deformant si cea a fundamentalei
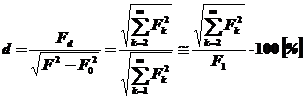 . (13)
. (13)
d) Distorsiunea armonica totala , se defineste in mod similar coeficientului global de distorsiune cu deosebirea ca se iau in considerare primele 40 de armonice
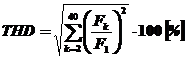 . (14)
. (14)
e) Distorsiunea armonica partial ponderata, introdus pentru a se asigura ca odata cu cresterea rangului, armonicile descresc este definit de relatia
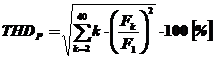 (15)
(15)
f) Coeficientul
de deformare al undei periodice nesinusoidale, ![]() , are expresia
, are expresia
![]() . (16)
. (16)
unde
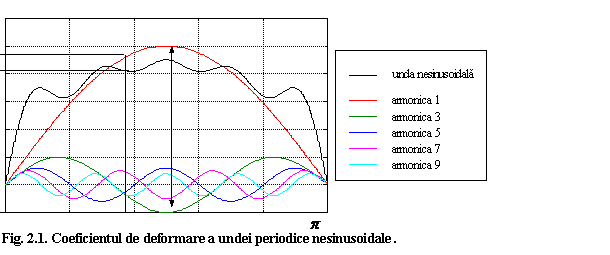
a reprezinta ordonata curbei reprezentative a undei periodice date;
b reprezinta ordonata curbei reprezentative a armonicii fundamentale a undei date, corespunzand la aceeasi abscisa ca si pentru "a";
c reprezinta amplitudinea curbei reprezentative a armonicii fundamentale, a, b, c fiind reprezentati in figura 1.
1.3. Puterile absorbite in regim deformant de un dipol
Potrivit teoriei puterilor in regim deformant dezvoltata de prof. C. Budeanu in continuare se vor prezenta relatiile de definire a puterilor absorbite de un dipol in regim nesinusoidal [10]:
![]()
![]()
![]()
a) Puterea aparenta absorbita de un receptor in regim nesinusoidal se poate defini in acelasi mod ca in regim sinusoidal, prin produsul valorilor efective ale tensiunii si curentului
![]() . (17)
. (17)
Calculul valorilor efective ale curentului si tensiunii se face potrivit relatiilor
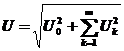 , (18
a)
, (18
a)
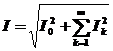 . (18
b)
. (18
b)
b)Puterea activa absorbita de un dipol receptor alimentat cu energie electrica, astfel incat tensiunea la borne si curentul sa fie nesinusoidal, este media pe o perioada a puterii instantanee absorbite de el
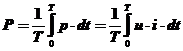 . (19)
. (19)
Se poate demonstra [95], [96] ca puterea activa este egala cu suma dintre produsul termenilor constanti (puterea de curent continuu) si suma puterilor active corespunzatoare armonicilor potrivit relatiei
![]() . (20)
. (20)
c) Puterea reactiva absorbita de un dipol in regim nesinusoidal este egala cu suma puterilor reactive corespunzatoare armonicelor
![]() (21)
(21)
d)Puterea deformanta, specifica regimului periodic nesinusoidal este definita de relatia:
![]() (22)
(22)
si are expresia
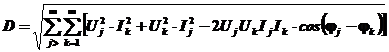 (23)
(23)
Pe baza puterilor definite astfel in regim nesinusoidal se definesc:
a) Factorul de putere in regim nesinusoidal ca raportul dintre puterea activa si cea aparenta
![]() . (24)
. (24)
b) Factorul reactiv
![]() . (25)
. (25)
c) Factorul deformant
![]() . (26)
. (26)
1.4. Definirea puterilor in retelele de distributie trifazate care functioneaza in regimuri nesimetrice si nesinusoidale
Avand in vedere ca instalatia electrica a cuptorului cu arc poate fi asimilata unui consumator de putere mare dezechilibrat, regimul de functionare al retelei va fi unul nesimetric si nesinusoidal. Din acest motiv este utila definirea puterilor si a factorilor de putere in regim trifazat nesimetric si nesinusoidal
Conform IEEE Working Group on nesinusoidal situation , in sistemele trifazate sunt definite urmatoarele:
Puterea aparenta echivalenta Se
![]() ,
,
unde
![]() , (28 a)
, (28 a)
![]() (28 b)
(28 b)
pentru retelele cu patru conductoare si
![]()
in cele cu trei conductoare.
Tensiunea Ue si curentul Ie, ca valori efective, prezinta cate doua componente - una corespunzatoare fundamentalei si alta nefundamentalei:
![]() , (30 a)
, (30 a)
![]() , (30 b)
, (30 b)
unde
![]() , (31 a)
, (31 a)
![]() , (31 b)
, (31 b)
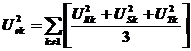 , (32 a)
, (32 a)
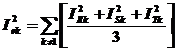 . (32 b)
. (32 b)
Ca
urmare si puterea aparenta are doua componente, una
fundamentala ![]() si alta
nefundamentala
si alta
nefundamentala![]() , adica
, adica
![]() .
.
Se defineste distorsiunea armonica totala echivalenta (de fapt reziduul deformant - Total Harmonic Distorsion) pentru tensiune respectiv curent ca fiind
![]() si (34.a)
si (34.a)
![]() (34.b)
(34.b)
si corespunzator puterea aparenta nefundamentala normalizata
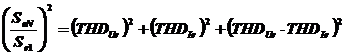 .
.
Puterea
aparenta fundamentala ![]() poate fi divizata
in doi termeni unul corespunzator secventei directe fundamentale
poate fi divizata
in doi termeni unul corespunzator secventei directe fundamentale ![]() si altul
corespunzator puterii aparente dezechilibrate fundamentale (puterii
aparente de nesimetrie pe fundamentala)
si altul
corespunzator puterii aparente dezechilibrate fundamentale (puterii
aparente de nesimetrie pe fundamentala) ![]() adica:
adica:
![]() .
.
Puterea aparenta fundamentala se poate descompune de asemenea in componentele activa respectiv reactiva.
Gradul de poluare armonica se apreciaza dupa marimea raportului
![]() .
.
Gradul de poluare nesimetrica se apreciaza prin raportul
![]() .
.
In aceste conditii se defineste factorul de putere fundamental KF1, prin relatia
![]()
si factorul de putere total
![]() ,
,
relatii in care ![]() reprezinta
puterea activa echivalenta pe fundamentala,
reprezinta
puterea activa echivalenta pe fundamentala, ![]() puterea activa
disipata pe armonici iar
puterea activa
disipata pe armonici iar ![]() si
si ![]() componentele directa, inversa respectiv homopolara a puterii active pe
fundamentala.
componentele directa, inversa respectiv homopolara a puterii active pe
fundamentala.
1.5. Criterii pentru definirea factorului de putere in regim deformant si dezechilibrat
In literatura de specialitate sunt evidentiate cateva criterii care trebuie sa stea la baza definitiei unui factor de putere in regim armonic . Cum acest regim in sistemele trifazate apare insotit si de cel nesimetric se poate vorbi de un factor de putere definit in regim deformant si dezechilibrat. Astfel criteriile sunt:
Factorul de putere trebuie sa permita aprecierea gradului de utilizare a puterii active disponibile pentru un receptor alimentat de la retea. De regula prin putere disponibila activa maxima se intelege puterea pe care receptorul o poate primi de la generatoarele ce debiteza in retea fara a determina pierderi suplimentare in retea, fata de pierderile pe care le determina alimentarea sa reala;
Factorul de putere trebuie sa dea informatii despre asa numitul consum tehnologic din retea determinat de alimentarea unui receptor deformant cu o anumita putere activa;
Factorul de putere, prin definitia lui, trebuie sa contina indicatii privind caile de aducere a valorii sale la valoarea optimala;
In regim permanent (sinusoidal, simetric), definitia trebuie sa se reduca la definitia clasica, cunoscuta;
Factorul de putere trebuie sa poata fi masurat cat mai simplu, cu mijloacele de masura deja existente fara a reclama mijloace suplimentare. De asemenea urmarirea lui trebuie sa se realizeze prin normativele deja existente.
Aceste criterii trebuie privite intr-un tot unitar. La definirea factorului de putere, in literatura se porneste de obicei de la unul dintre aceste criterii si se verifica apoi cum sunt indeplinite celelalte. Desi se parea ca factorul de putere este o marime proprie consumatorului, prin criteriile impuse rezulta ca valoarea lui depinde de interactiunea consumatorului cu reteaua.
Definitia factorului de putere trebuie sa contina informatii referitoare la caracteristicile regimului nesimetric si nesinusoidal. Acestea sunt reflectate de obicei prin coeficientii de nesimetrie si nivelul armonicelor.
Daca se are in vedere gradul de utilizare al puterii active disponibile si, legat de aceasta, circulatia puterilor de secventa si a celor armonice in retea factorul de putere poate fi definit ca fiind:
![]() ,
,
sau
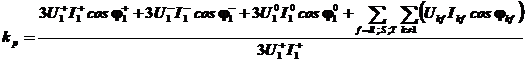 .
.
Daca se introduc marimile caracteristice regimului dezechilibrat si nesinusoidal, expresia lui kp devine:
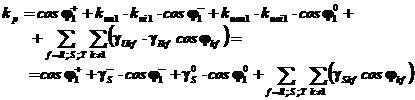
unde ![]() sunt coeficientii
de disimetrie respectiv de asimetrie pe fundamentala, pentru tensiuni
si curenti, adica:
sunt coeficientii
de disimetrie respectiv de asimetrie pe fundamentala, pentru tensiuni
si curenti, adica:
![]()
![]()
![]()
![]()
![]() - nivelul armonicii k de tensiune si curent, pe
faza f
- nivelul armonicii k de tensiune si curent, pe
faza f
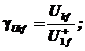
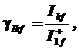
![]() - ponderile relative
ale puterilor aparente inversa, homopolara si armonice
fata de puterea aparenta directa pe fundamentala
- ponderile relative
ale puterilor aparente inversa, homopolara si armonice
fata de puterea aparenta directa pe fundamentala
![]()
![]()
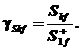
Se defineste
factorul de putere fundamental sau de simetrie, care tine cont de consumul de putere reactiva pe secventa directa a armonicii fundamentale,
![]()
factorul de putere nesimetric care tine seama de nesimetria regimului fundamentalei,
![]()
factorul de putere deformant, care tine seama de circulatia puterilor active armonice pe toate cele trei faze.
![]()
Se poate scrie deci:
![]()
De
regula ![]() si
si ![]() , astfel incat in regimuri reale, necompensate
, astfel incat in regimuri reale, necompensate ![]() .
.
Valoarea
factorului de putere kp ramane ![]() in conditiile in
care
in conditiile in
care ![]() si
si ![]() . Valoarea
. Valoarea ![]() se realizeaza
prin adoptarea simultana acelor trei masuri: compensarea puterii reactive, echilibrarea sarcinii
si filtrarea armonicilor. Cele
trei masuri nu sunt independente, ele depinzand de structura interna
a consumatorului. In unele cazuri factorul de putere poate deveni supraunitar,
fapt care indica absorbtia de putere activa nesimetrica
si de putere activa reziduala de la alte receptoare
dezechilibrate si deformante.
se realizeaza
prin adoptarea simultana acelor trei masuri: compensarea puterii reactive, echilibrarea sarcinii
si filtrarea armonicilor. Cele
trei masuri nu sunt independente, ele depinzand de structura interna
a consumatorului. In unele cazuri factorul de putere poate deveni supraunitar,
fapt care indica absorbtia de putere activa nesimetrica
si de putere activa reziduala de la alte receptoare
dezechilibrate si deformante.
Intr-o situatie mai simpla cand sistemul de tensiuni este mai putin dezechilibrat iar curbele tensiunilor de faza sunt putin distorsionate se poate defini un factor de putere avandu-se in vedere pierderile de putere determinate de curentii nesimetrici si nesinusoidali in reteaua de alimentare, astfel:
![]() ,
,
unde ![]() , sunt pierderile de putere pe linia de alimentare (elementul
de retea din amonte) in situatia compensarii puterii reactive,
echilibrarii si filtrarii, adica:
, sunt pierderile de putere pe linia de alimentare (elementul
de retea din amonte) in situatia compensarii puterii reactive,
echilibrarii si filtrarii, adica:
![]() ,
,
R1 fiind rezistenta fundamentala a liniei.
In ceea
ce priveste pierderile ![]() , in retelele cu patru conductoare, acestea au expresia:
, in retelele cu patru conductoare, acestea au expresia:
![]() ,
,
RNk fiind rezistenta conductorului neutru in planul armonicii k
Inlocuind
pe ![]() dat de relatia in expresia lui kp data de relatia se obtine:
dat de relatia in expresia lui kp data de relatia se obtine:
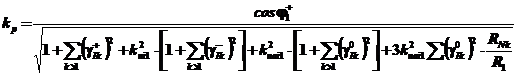 ,
,
unde ![]() sunt nivelurile
armonicilor de curent de secventa directa, inversa si
homopolara in planul armonicii k, adica:
sunt nivelurile
armonicilor de curent de secventa directa, inversa si
homopolara in planul armonicii k, adica:
![]() ;
; ![]() ;
; ![]() .
.
Daca linia de alimentare este fara conductor neutru, curentul homopolar este nul, si toate relatiile de mai sus vor capata forme mai simple.
Desi simplista, intrucat nu considera nesimetria si deformarea tensiunilor , relatia ramane sugestiva din punct de vedere calitativ prin aceea ca ofera o dependenta directa a factorului de putere cu gradul de nesimetrie si de nivelul armonicilor curentilor.
Arcul electric alimentat la tensiune alternativa element neliniar de circuit al cuptoarelor electrice trifazate
 1.
Caracteristici ale arcului electric alimentat la tensiune alternativa
1.
Caracteristici ale arcului electric alimentat la tensiune alternativa
Asa cum s-a prezentat in se poate considera ca pe durata arderii arcului electric alimentat cu tensiune alternativa, schema echivalenta a circuitului de alimentare poate fi reprezentata sub forma indicata in figura
In aceasta schema r si L reprezinta rezistenta respectiv inductivitatea echivalenta a circuitului de alimentare iar RA si uA rezistenta arcului electric, respectiv tensiunea la bornele arcului.
Forma de variatie a marimilor electrice din schema echivalenta a circuitului de alimentare este prezentata in figura 3. Analizand forma de variatie a marimilor electrice se pot trage urmatoarele concluzii:
pe durata arderii arcului electric tensiunea uA la bornele acestuia este practic constanta si deoarece curentul este variabil rezulta ca arcul electric reprezinta un receptor neliniar,
tensiunea uA la bornele arcului electric si curentul i din circuit sunt in faza rezultand ca arcul electric are caracter rezistiv,
curentul electric din circuit trece de doua ori prin zero in fiecare perioada a tensiunii alternative aplicate, ceea ce determina stingerea si reaprinderea arcului electric cu o frecventa dubla fata de cea a tensiunii aplicate,
tensiunea de amorsare Uam a arcului electric este mai mare decat valoarea de
functionare UA 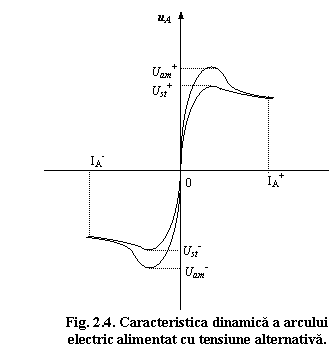
curentul electric din circuit este periodic, dar nesinusoidal.
arcul electric
alimentat cu tensiune electrica alternativa prezinta caracter
redresant [1]. Aceasta consta in faptul ca
daca descarcarea se produce intre un electrod (in mod uzual de
grafit) si metalul care urmeaza a fi incalzit, datorita
proprietatilor termofizice diferite ale celor doua materiale (temperatura
electrodului de grafit este mai mare ca cea a metalului de procesat), tensiunea
de amorsare a arcului electric in semiperioada care metalul de incalzit
este catod este mai mare decat tensiunea de amorsare in semiperioada in care
electrodul de grafit este catod, adica ![]() . In mod asemanator, pentru tensiunea de stingere
in cele doua semiperioade este valabila relatia
. In mod asemanator, pentru tensiunea de stingere
in cele doua semiperioade este valabila relatia ![]() . Din acest motiv amplitudinea curentului electric in cele
doua semiperioade este diferita si anume este mai mare in
semiperioada in care electrodul din grafit este catod.
. Din acest motiv amplitudinea curentului electric in cele
doua semiperioade este diferita si anume este mai mare in
semiperioada in care electrodul din grafit este catod.
In figura 4 este reprezentata caracteristica
dinamica a arcului electric alimentat cu tensiune alternativa,
caracteristica obtinuta pe baza curbelor de variatie a
marimilor electrice ![]() si
si ![]() prezentate in figura 3.
Caracterul redresant al arcului electric este pus in evidenta prin
faptul ca valoarea tensiunii de amorsare si de stingere este
diferita in cele doua semialternante.
prezentate in figura 3.
Caracterul redresant al arcului electric este pus in evidenta prin
faptul ca valoarea tensiunii de amorsare si de stingere este
diferita in cele doua semialternante.
Din punct de vedere al curentului arcului electric
arderea arcului electric poate avea loc in regim de curent intrerupt
sau curent neantrerupt. Arderea arcului electric in regim de
curent intrerupt determina o functionare instabila a acestuia
iar curba curentului este puternic deformata [1]. Din acest motiv
este necesar ca arcul electric sa arda fara pauze. In [1]
a fost determinata conditia de ardere a arcului electric
fara pauze in ipotezele simplificatoare ca ![]() si tensiunea de alimentare este sinusoidala
si tensiunea de alimentare este sinusoidala
![]() .
.
Aceasta conditie este data de
![]() (56)
(56)
care conduce la
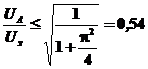 , (57)
, (57)
rezultand ca pentru a avea curent neantrerupt este necesar ca instalatia sa functioneze cu un factor de putere natural
![]() . (58)
. (58)
Copyright © 2025 - Toate drepturile rezervate