 | Aeronautica | Comunicatii | Constructii | Electronica | Navigatie | Pompieri |
| Tehnica mecanica |
1. Regimurile de functionare ale SRA
Regimul normal de functionare al elementelor si sitemelor automate este acela in care toate marimile caracteristice ale acestora prezinta variatii pronuntate in raport cu timpul, denumit regim dinamic. In cazul in care marimile sistemului sunt constante sau au variatii lente in timp se obtine regimul stationar.
Regimul dinamic este produs de variatia marimilor de intrare si a perturbatiilor, dispozitivul de automatizare avand ca scop restabilirea echilibrului, adica aducerea sistemului in regim stationar. Regimul stationar este limita spre care tinde regimul dinamic.
Dependenta dintre marimea de intrare cauza si marimea de iesire efect se numeste ecuatia intrare-iesire a sistemului, denumita si caracteristica sistemului.
Pentru cazul sistemelor liniare, caracteristica dinamica este data de ecuatia intrare-iesire a sistemului sub forma operationala :
![]()
unde matricele A, B, C si D corespund ecuatiilor canonice sub forma implicita, iar G(s) este matricea de transfer dinamica.
Pentru a obtine caracteristica statica
se face limita pentru ![]() sau
sau ![]() asupra caracteristicii dinamice :
asupra caracteristicii dinamice :
![]()
unde expresia ![]() este matricea de
transfer statica.
este matricea de
transfer statica.
In cazul sistemelor mono I/E, caracteristica dinamica este data de functia de transfer :
![]()
iar pentru regim stationar caracteristica este data de coeficientul de transfer static :
![]()
rezultand ca pentru sistemele mono I/E caracteristica statica e o dreapta (fig.1) data de relatia :
![]()
Coeficientul de transfer static poarta numele de amplificare la amplificatoare si de sensibilitate la traductoare.
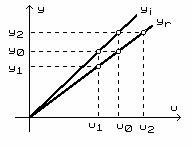
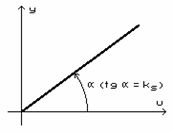
Fig.1 Fig.2.
Pentru imbunatatirea caracteristicilor statice ale elementelor de automatizare si pentru folosirea corecta a acestora cand se concepe un sistem automat, trebuie sa realizam urmatoarele doua etape :
- cunoasterea caracteristicii statice y = f(u);
- imbunatatirea caracteristicii statice daca aceasta nu ne satisface.
a) Caracteristica statica se cunoaste dupa fisa tehnica a elementului de automatizare data de producator, care este de fapt caracteristica statica ideala yi = f1(u). Datorita modificarilor parametrilor interni si externi ai pieselor din care este constituit elementul de automatizare, caracteristica statica se modifica devenind caracteristica statica reala yr = f2(u).
Daca aplicam asupra elementului de automatizare marimea de intrare u0, atunci conform caracteristicii ideale ar trebui sa obtinem iesirea y1, dar conform caracteristicii reale se obtine iesirea y0 (fig.2). Aceasta iesire ar corespunde marimii de intrare u2 > u0 pentru caracteristica ideala. In realitate, pentru obtinerea marimii y1 trebuie sa aplicam la intrare marimea u1 < u0. Daca am aplica la intrare marimea u2 > u0 s-ar obtine conform caracteristicii stastice reale marimea de iesire y2.
Dupa cum se vede, in domeniul [u1, u2] utilizatorul nu poate sti la proiectare care va fi adevarata marime de iesire. Deci avem o zona de insensibilitate Δu = u2 - u1, marimile u1 si u2 din jurul valorii u0 numindu-se praguri de sensibilitate.
Se numeste eroare a unui element, variatia marimii de iesire cauzata de modificarile interne si externe la o marime de intrare constanta. Avem eroarea absoluta sau toleranta elementului de automatizare :
![]()
si eroarea relativa :
![]()
Domeniul cuprins intre cele doua caracteristici, ideala si reala, se numeste spatiu de eroare.
Elementele de automatizare se construiesc cu o anumita toleranta Δy cunoscuta. Pentru a folosi corect un asemenea element de automatizare trebuie ca variatia marimii de intrare in elementul de automatizare sa fie mult mai mare ca zona de insensibilitate Δu
b) Imbunatatirea caracteristicii statice se face prin practicarea unei legaturi inverse de la iesire la intrare (fig.3) printr-un bloc care are coeficientul de transfer static β numit si factor de reactie. Blocul de pe calea directa are coeficientul de transfer static ks. Din scema bloc prezentata se poate scrie :
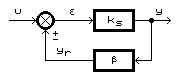
Fig.3.
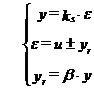
rezultand caracteristica statica a elementului de automatizare cu reactie :
![]()
unde kr este coeficientul de transfer static al elementului cu reactie.
Daca reactia este pozitiva rezulta kr > ks, reactia pozitiva avand caracter amplificator, imbunatateste sensibilitatea in detrimentul stabilitatii la perturbatii. Daca reactia este negativa rezulta kr < ks ceea ce are ca efect reducerea amplificarii, dar elementul devine mai liniar si influienta perturbatiilor este eliminata, legatura de reactie negativa avand caracter stabilizator.
2. Principiul analizei sistemelor automate liniare
Prin analiza sistemelor automate se intelege determinarea calitatilor si performantelor acestora pe baza cunoasterii structurii sistemelor sau a modelului lor matematic. Structura unui sistem automat se cunoaste prin determinarea schemei de principiu a sistemului. Modelul matematic al unui sistem automat reprezinta totalitatea relatiilor matematice care se stabilesc intre marimile de intrare si de iesire ale acestuia.
Modelul matematic se poate determina sub trei forme :
- modelul matematic primar;
- modelul matematic operational;
- modelul matematic de stare.
Modelul matematic primar reprezinta o ecuatie diferentiala sau un sistem de ecuatii diferentiale stabilite intre vectorul de iesire si vectorul de intrare al sistemului. Pentru a obtine aceste ecuatii intrare-iesire trebuie sa cunoastem structura sistemului. Cunoscand structura si bazandu-ne pe diverse legi din electrotehnica, mecanica, electronica putem scrie relatiile dintre marimile sistemului iar apoi eliminand marimile intermediare vom obtine ecuatiile intrare-iesire ale sistemului.
Modelul matematic operational este dat prin ecuatia operationala intrare-iesire de forma :
![]()
unde G(s) este matricea de transfer pentru sistemele liniare multi I/E :
![]()
iar pentru sistemele liniare mono I/E marimile G(s) reprezinta functia de transfer.
Modelul matematic de stare este dat de ecuatiile de stare :
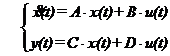
Pentru a efectua analiza unui sistem automat este suficient sa cunoastem unul din aceste trei tipuri de modele matematice ale sistemului pentru ca putem sa le obtinem si pe celelalte doua.
Daca se cunoaste modelul matematic primar atunci se aplica transformata Laplace in conditii initiale nule asupra ecuatiilor diferentiale intrare-iesire, obtinandu-se matricea de transfer pentru sistemele multi I/E sau functia de transfer pentru sistemele mono I/E, deci va rezulta modelul matematic operational.
Daca se cunoaste matricea de transfer G(s), deci modelul matematic operational, vom putea obtine modelul matematic de stare facand o realizare standard RSCC sau RSCO.
De la modelul matematic de stare, prin intermediul transformarii rezolvente REZ, putem trece la modelul matematic primar :
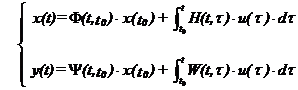
Analiza sistemelui automat isi propune, plecand de la unul dintre cele 3 modele matematice, determinarea calitatilor dinamice ale sistemului. Analiza parcurge doua etape :
- analiza in domeniul timpului;
- analiza in domeniul frecventei.
a) Analiza in domeniul timpului se realizeaza presupunand ca se cunoaste modelul matematic operational (2.10) si consideram ca la intrare vom aplica un semnal treapta unitara :
![]()
unde h(t) reprezinta semnalul standard treapta unitara sau distributia lui Heawiside :
![]()
care are transformata
![]()
Se obtine :
![]()
din care, dupa desfacerea in
expresii simple si prin aplicarea transformatei inverse
![]()
care urmeaza a fi reprezentat grafic (fig.4.a), din graficul raspunsului rezultand concluzii cu privire la comportarea iesirii in cazul modificarii marimii de intrare.
b) Analiza in domeniul frecventei consta in analiza Fourier a functiei de transfer G(s). Pentru aceasta aplicam transformata Fourier s = j ∙ ω asupra functiei de transfer si rezulta o functie de variabila complexa :
![]()
unde : U(ω) si V(ω) - partea reala si partea imaginara a functiei G(j∙ω) :
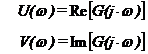
│G(j∙ω)│ - modulul functiei G(j∙ω) :
![]()
φ(ω) - defazajul sistemului sau argumentul functiei G(j∙ω) :
![]()
Plecand de la transformata Fourier a functiei de transfer, in practica se utilizeaza trei tipuri de grafice si anume :
- Graficul
locului de transfer sau diagrama
Nyquist care reprezinta graficul in coordonate carteziene (fig.4.b) a
functiei G(j∙ω , adica graficul parsii imaginare V(ω in functie de partea reala U(ω atunci cand pulsatia ![]() sau doar pentru valori pozitive ale
pulsatiei
sau doar pentru valori pozitive ale
pulsatiei ![]() deoarece graficul pentru valori negative ale
pulsatiei
deoarece graficul pentru valori negative ale
pulsatiei ![]() este simetric fata de abcisa.
Acest grafic poate avea si o reprezentare polara a functiei G(j∙ω daca se calculeaza pentru fiecare valoare a lui
este simetric fata de abcisa.
Acest grafic poate avea si o reprezentare polara a functiei G(j∙ω daca se calculeaza pentru fiecare valoare a lui ![]() cate un segment │G(j∙ω si cate un unghi φ ω , varful segmentului reprezentand un punct
al graficului. Graficul locului de transfer sau diagrama Nyquist da
informatii cu privire la amplificarea sistemului in functie de
pulsatia ω,
amplificarea fiind data de distanta de la origine la grafic.
cate un segment │G(j∙ω si cate un unghi φ ω , varful segmentului reprezentand un punct
al graficului. Graficul locului de transfer sau diagrama Nyquist da
informatii cu privire la amplificarea sistemului in functie de
pulsatia ω,
amplificarea fiind data de distanta de la origine la grafic.
- Graficul atenuarii sau diagrama Bode care reprezinta graficul atenuarii la scara logaritmica. Atenuarea este
data de logaritmul natural sau zecimal al modulului │G(j∙ω calculat in neperi Np sau decibeli dB in
functie de pulsatia ![]() . Daca
logaritmul modulului este natural atenuarea se masoara in neperi Np
si pulsatia variaza prin puteri ale lui 2 (prin octave). Daca logaritmul modulului este zecimal
si se amplifica prin 20,
atenuarea se masoara in decibeli dB si pulsatia
variaza prin puteri ale lui 10 (prin
decade). Cel mai folosit este graficul atenuarii in decibeli (fig.4.c).
. Daca
logaritmul modulului este natural atenuarea se masoara in neperi Np
si pulsatia variaza prin puteri ale lui 2 (prin octave). Daca logaritmul modulului este zecimal
si se amplifica prin 20,
atenuarea se masoara in decibeli dB si pulsatia
variaza prin puteri ale lui 10 (prin
decade). Cel mai folosit este graficul atenuarii in decibeli (fig.4.c).
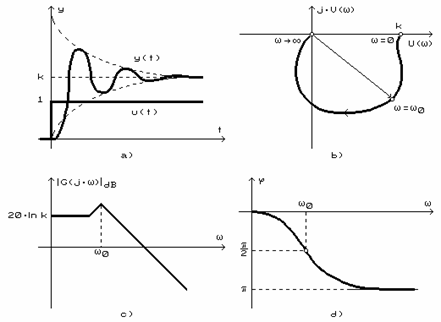
Fig.4.
Graficul atenuarii sau diagrama Bode da informatii cu privire la atenuarea sistemului in functie de pulsatia ω. Atenuarea este constanta cand graficul are panta nula, creste cand panta este pozitiva si scade cand panta este negativa. Deci :
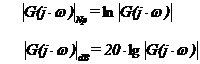
iar relatia de transformare a atenuarii din neperi in decibeli, stiind ca 1 Np = 8,686 dB, este :
![]()
- Graficul defazajului care reprezinta graficul defazajului φ in functie de pulsatia ω (fig.2.4.d). Acesta da informatii cu privire la defazajul dintre iesirea si intrarea sistemului in functie de pulsatia ω.
Exemplu : analizam un element de automatizare de tip traductor de presiune (fig.5). S-au facut notatiile : S - suprafata pistonului, U - tensiunea la bornele potentiometrului, L - lungimea potentiometrului, F1 - forta activa datorata presiunii, F2 - forta elastica a resortului de constanta de elasticitate; F3 - forta de franare vascoasa a cilindrului de franare cu constanta, F4 - forta de inertie cauzata de masele in miscare, u - presiunea p a uleiului (marimea de intrare), y - tensiunea culeasa la iesirea potentiometrului (marimea de iesire), x - deplasarea echipamentului mobil odata cu pistonul (marime intermediara).
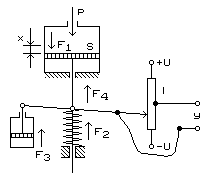
Fig.5.
Echilibrul fortelor si fortele care intervin sunt :
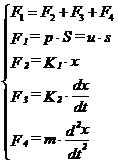
rezultand :
![]()
Tensiunea la bornele potentiometrului este :
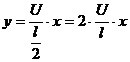
rezultand :
![]()
Inlocuind marimea intermediara in ecuatia de echilibru si impartind relatia prin coeficientul iesirii y, obtinem modelul matematic primar :
![]()
Aplicand transformata Laplace se obtine :
![]()
sau :
![]()
rezultand modelul matematic operational :
![]()
unde : k - coeficientul de transfer al traductorului :
![]()
T1 si T2 - constantele de intarziere ale traductorului :
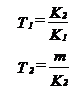
Rezulta functia de transfer a traductorului de presiune considerat :
![]()
unde : ω - pusatia proprie a traductorului :
![]()
ξ - factorul de amortizare al traductorului :
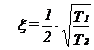
Pentru a face o realizare RSCC vom identifica coeficientii : a0 = ω02, a1 = 0, b0 = ω02, b1 = 2∙ξ∙ω0, n = 2 deci matricile vor fi :
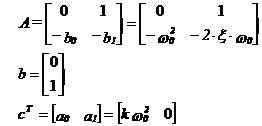
rezultand modelul matematic de stare :
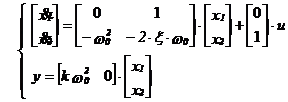
sau :
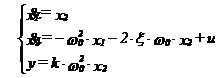
din care se obtine schema bloc a realizarii RSCC (fig.6.).
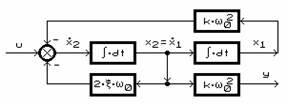
Fig.6.
Facem analiza in domeniul timpului, adica determinam raspunsul la intrare treapta unitara (raspunsul normal) :
![]()
si aplicand trasformata
inversa
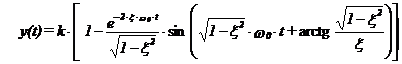
Pentru analiza in domeniul frecventei aplicam transformata Fourier asupra functiei de trasfer:
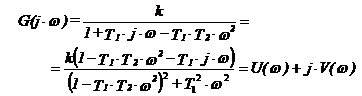
si obtinem partea reala si partea imaginara :
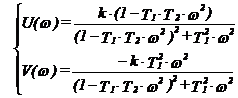
atenuarea :
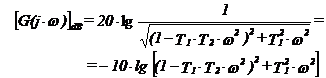
si defazajul :
![]()
pe baza carora se traseaza graficul locului de transfer sau diagrama Nyquist (fig.4.b), graficul atenuarii sau diagrama Bode(fig.4.c) si graficul defazajului (fig.4.d).
In urma analizei elementului rezulta o serie de proprietati dinamice si anume :
- elementul este de tip oscilator (PI2);
- la orice variatie a intrarii, iesirea executa cateva oscilatii amortizate, dupa care urmareste intrarea multiplicata cu constanta k;
- amplificarea traductorului este maxima pentru ω ω dupa care amplificarea scade si tinde la zero cu cresterea frecventei;
- pana la ω ω atenuarea este constanta dupa care traductorul este puternic atenuator;
- iesirea este in urma intrarii cu un defazaj care tinde de la zero la π cu cresterea frecventei.
3. Stabilitatea sistemelor automate liniare. Concept. Teorema de stabilitate
Stabilitatea reprezinta una din cele mai importante calitati ale sistemelor automate deoarece sistemele automate care nu sunt stabile nu se utilizeaza practic. Stabilitatea este capacitatea unui sistem automat ca dupa disparitia perturbatiilor orice semnal de intrare limitat sa produca un semnal de stare si un semnal de iesire limitat.
Conceptul de stabilitate astfel definit prezinta doua aspecte si anume :
stabilitate BIBS (boundet input - boundet state : intrare limitata - stare limitata);
stabilitate BIBO (boundet input - boundet output : intrare limitata - iesire limitata).
Stabilitatea BIBO este mai cuprinzatoare pentru ca marimea de stare poate fi considerata cuprinsa in marimea de iesire deoarece, in cazul sistemelor liniare y = f(x) este liniara.
Definitie : Un sistem automat este asimptotic stabil daca, dupa
disparitia perturbatiei si anularea intrarii, iesirea
tinde spre zero. Un sistem este limitat
stabil daca, dupa disparitia perturbatiei si
anularea intrarii, iesirea tinde spre o
Sistemele liniare si stationare controlabile si observabile sunt descrise de ecuatiile canonice sub forma explicita :
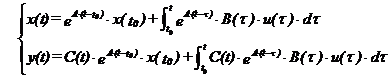
Din definitia stabilitatii intrarea este nula si, indiferent de tipul stabilitatii BIBO sau BIBS, se obtine :
- pentru stabilitate asimptotica : ![]()
- pentru stabilitate limitata : ![]()
sa aiba norma limitata, adica stabilitatea trebuie analizata prin marimea de stare.
Teorema de stabilitate sub forma temporala : Conditia necesara si suficienta ca un sistem liniar si stationar sa fie asimptotic stabil este ca toate valorile proprii sau radacinile λi ale ecuatiei caracteristice │λ ∙ I - A│ = 0 sa fie simple si sa aibe partea reala negativa; daca o radacina este nula sau o perece de radacini sunt pur imaginare (complexe conjugate cu partea reala nula) sistemul este limitat stabil; in rest sistemul este instabil.
Demonstratie : Se pleaca de la expresia matricei A ∙ (t - to) pe care o putem scrie :
![]()
unde λ reprezinta vectorul valorilor proprii ale matricei A :
![]()
Valorile proprii λi sunt valorile pentru care are sens ecuatia :
![]()
adica :
![]()
de unde rezulta valorile proprii λi
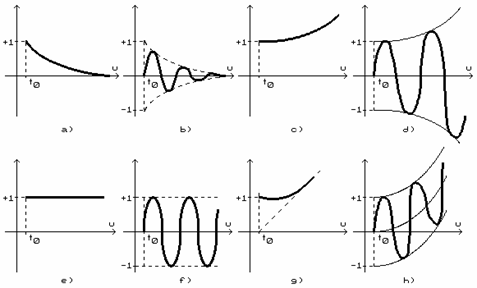
Fig.7.
Putem scrie :
![]()
de unde se obtin urmatoarele cazuri :
a) λi = - α (radacini simple reale negative) :
![]()
rezultand stabilitate asimptotica (fig.7.a);
b) λi = - α ± j ∙ β (radacini simple complexe conjugate cu partea reala negativa) :
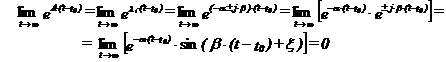
rezultand stabilitate asimptotica (fig.7.b);
c) λi = + α (radacini simple reale pozitive) :
![]()
rezultand instabilitate (fig.7.c);
d) λi α ± j ∙ β (radacini simple complexe conjugate cu partea reala pozitiva) :
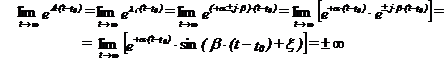
rezultand instabilitate (fig.7.d);
e) λi = 0 (radacina simpla reala nula) :
![]()
rezultand stabilitate limitata (fig.7.e);
f) λi = ± j ∙ β (radacini simple complexe conjugate cu partea reala nula) :
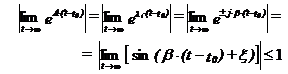
rezultand stabilitate limitata (fig.7.f);
g) λi multipla (ordinul de multiplicitate mi >1) :
![]()
rezultand instabilitate (fig.7.g si h).
Teorema de stabilitate sub forma operationala : Conditia necesara si suficienta ca un sistem liniar si stationar sa fie asimtotic este ca toti polii matricei de transfer a sistemului sa fie simpli si sa aiba partea reala negativa. Daca un pol este nul sau o pereche de poli complex conjugati au partea reala nula sistemul este limitat stabil. In rest sistemul este instabil.
Demonsratie : se pleaca de la expresia matricei de transfer :
![]()
de unde se observa ca polii matricei de transfer G(s) se obtin ca radacini ale numitorului, deci ca radacini ale ecuatiei │s ∙ I - A│ = 0 care este identica cu ecuatia caracteristica │λ ∙ I - A│ = 0. Rezulta ca polii si sunt identici cu valorile propri λi si deci demonstratia este identica cu cea anterioara de la teorema sub forma temporala.
3.1. Criteriul de stabilitate Leapunov
Enunt : Un sistem liniar si stationar este asimptotic stabil daca si numai daca pentru o matrice P pozitiv definita, solutia Q a ecuatiei matriceale algebrice de forma :
![]()
este pozitiv definita, sau este limitat stabil daca Q este pozitiv semidefinita.
Demonstratie : Se considera functia matriceala vectoriala Leapunov
![]()
care reprezinta o familie de sfere cu originea in centrul spatiului de stare.
Pentru ca sistemul sa fie stabil trebuie ca traiectoria sistemului in evolutie libera, traiectorie data de solutia x(t) a ecuatiei :
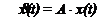
sa se apropie de origine, adica sa intersecteze familia de sfere sub un unghi mai mare decat π (unghiul dintre tangenta la traiectoria sistemului si normala la sfere) :
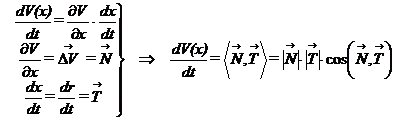
3.2. Criteriul de stabilitate Ruth-Hurwitz
Acesta este un criteriu de stabilitate algebric care se mai numeste si criteriul coeficientilor ecuatiei caracteristice pentru ca la cercetarea stabilitatii se analizeaza existenta si semnul tuturor coeficientilor ecuatiei caracteristice precum si determinantii construiti cu acesti coeficienti.
Enunt : Conditia necesara si suficienta ca un sistem liniar si stationar sa fie asimptotic stabil este ca toti coeficientii ecuatiei caracteristice :
![]()
sa existe si sa fie pozitivi si toti determinantii minori extrasi dupa diagonala principala din matricea Hurwitz :
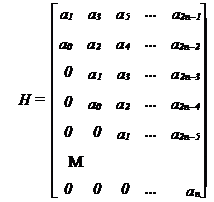
sa fie pozitivi :
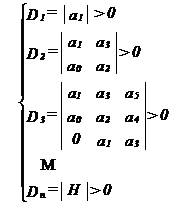
Daca un singur determinant este nul sistemul este limitat stabil. In rest sistemul este instabil. Daca sistemul este instabil se construieste sirul :
![]()
in care numarul de schimbari de semn ne arata numarul de radacini ale ecuatiei caracteristice aflate in semiplanul drept al planului complex, adica numarul de radacini cu partea reala pozitiva care dau instabilitate conform teoremei.
Demonstratie : Consideram ecuatia matriceala algebrica (de la criteriul Leapunov) :
![]()
in care consideram P = I. Atunci o solutie a acestei ecuatii este de forma :
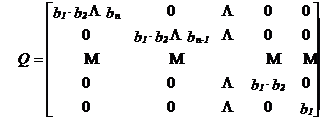
unde :
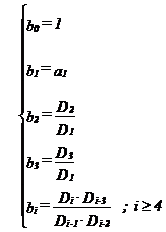
Pentru ca matricea Q sa fie pozitiv definita trebuie ca bi > 0; dar cum bi se obtin din matricea H cu ajutorul determinantilor minori Di rezulta demonstratia criteriului.
Observatie : Matricea Hurwitz are pe diagonala principala termenii a1, a2, a3, ,an. Rezulta ca dimensiunea matricei Hurwitz este dim H = n x n.
Observatie : Daca un determinant este nul, in calculele determinantilor superiori, acesta se considera egal cu ε si in final se face limita cand ε si se trag concluziile conforme criteriului.
3.3. Criteriul de stabilitate Mihailov-Leonhard
Acesta este un criteriu grafic frecvential deoarece pentru cercetarea stabilitatii se reprezinta graficul ecuatiei caracteristice F(s) = 1 + G(s) ∙ H(s) = 0 in coordonate carteziene (U(ω); j∙V(ω ) pentru diferite frecvente ale semnalului de intrare.
Enunt : Conditia necesara si suficienta ca un sistem liniar si stationar sa fie asimptotic stabil este ca graficul ecuatiei caracteristice in coordonate carteziene (U(ω); j∙V(ω ) sa parcurga in sens direct si succcesiv n cadrane atunci cand pulsatia ω ia valori de la 0 la +∞ (n - gradul ecuatiei caracteristice). Daca graficul trece o data prin origine in locul unui cadran atunci sistemul este limitat stabil. In rest sistemul este instabil.
Demonstratie : Se pleaca de la ecuatia caracteristica la care se considera a0 = 1 (daca nu, se imparte cu a0) :
![]()
unde si (i = 1 ÷ n) sunt radacinile ecuatiei caracteristice.
Aplicand transformata Fourier obtinem :
![]()
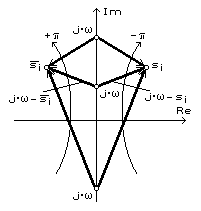
Fig.1.8.
In planul complex (fig.8) binomul (j ∙ ω - si) reprezinta diferenta a doi vectori care pleaca din origine : vectorul (j∙ω) plasat pe axa imaginara si vectorul si avand varful plasat oriunde in planul complex (dat de radacina ecuatiei caracteristice). Rezulta ca vectorul (j ∙ ω - si) are varful in punctul si, iar originea lui se deplaseaza de jos in sus pe axa imaginara, atunci cand ω ia valori de la -∞ la +∞. Ca urmare vectorul (j ∙ ω - si) va descrie un unghi egal cu +π daca radacina si este in semiplanul stang si -π daca radacina si este in semiplanul drept. Deci variatia argumentului ecuatiei caracteristice va fi :
![]()
unde ns si nd sunt numarul de radacini din semiplanul stang respectiv drept. Numarul total de radacini este :
![]()
rezultand :
![]()
Se obtine :
![]()
iar daca intervalul de variatie al pulsatiei se reduce la jumatate :
![]()
Pentru a avea stabilitate nu trebuie sa avem radacini in semiplanul drept (nd = 0) si rezulta:
![]()
ceea ce trebuia demonstrat, deoarece π reprezinta un cadran din planul complex.
3.4. Criteriul de stabilitate Nyquist-Neumark
Enunt :
Conditia necesara si suficienta ca un sistem inchis sa
fie asimptotic stabil este ca graficul functiei de transfer a sistemului
deschis in coordonate carteziene (U(ω); j∙V(ω ) sa inconjoare punctul critic (-1;
j∙0) de Np
ori in sens negativ cand ![]() , unde Np este numarul de poli
ai sistemului deschis din semiplanul drept (cu partea reala
pozitiva). Daca graficul trece o singura data prin punctul
critic (in loc sa-l inconjoare) sistemul este limitat stabil. In rest
sistemul este instabil.
, unde Np este numarul de poli
ai sistemului deschis din semiplanul drept (cu partea reala
pozitiva). Daca graficul trece o singura data prin punctul
critic (in loc sa-l inconjoare) sistemul este limitat stabil. In rest
sistemul este instabil.
Demonstratie : Consideram un sistem inchis (fig.9.a) care are functia de transfer :
![]()
Sistemul poate fi deschis prin taierea legaturii inverse (fig.9.b), sistemul deschis avand functia de transfer :
![]()
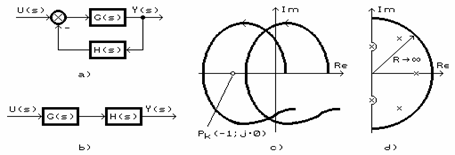
Fig.9.
Ecuatia caracteristica a sistemului inchis este :
![]()
rezultand :
![]()
sau, aplicand transformata Fourier :
![]()
Rezulta ca daca ecuatia caracteristica a sistemului inchis F(j∙ω) parcurge n cadrane, atunci functia de transfer a sistemului deschis Gd(j∙ω) va fi translatata cu -1 si deci va inconjura punctul (-1; j∙0) care este punctul critic al sistemului (fig.9.c).
Pentru o functie de variabila complexa, conform teoremei lui Cauchy, avem :
![]()
unde Nz si Np sunt numarul de zerouri si de poli ai functiei de variabila complexa f(s) in conturul inchis C pe care se face integrarea.
Integrala pe conturul inchis C dintr-o functie de variabila complexa f(s) este data de :
![]()
deoarece pe un contur inchis avem :
![]()
![]()
rezultand :
![]()
sau, dupa ce aplicam transformata Fourier :
![]()
Rezulta
ca graficul functiei complexe f(j∙ω) pentru ![]() descrie un numar
de unghiuri complete 2∙π
egal cu diferenta dintre numarul zerourilor si al polilor
functiei care se gasesc in conturul inchis C.
descrie un numar
de unghiuri complete 2∙π
egal cu diferenta dintre numarul zerourilor si al polilor
functiei care se gasesc in conturul inchis C.
Daca alegem conturul inchis C tocmai conturul lui Nyquist (semiplanul drept sau semicerc de raza infinita (fig.2.19.d), iar ca functie de variabila complexa tocmai functia de transfer a sistemului deschis Gd(j∙ω), obtinem :
![]()
si, deoarece zerourile nu influienteaza stabilitatea (Nz = 0), se obtine :
![]()
Deci graficul functiei de transfer a sistemului deschis va inconjura punctul critic in sens negativ de Np ori.
3.5. Criteriul de stabilitate matriceal
Criteriile de stabilitate studiate necesita analiza ecuatiei caracteristice si de multe ori se ajunge la dificultati mari. Recent s-a elaborat criteriul matriceal care se bazeaza pe analiza unei matrice provenite din matricea A din ecuatiile canonice sub forma implicita. Criteriul se refera la ridicari succesive la puteri a unei matrici si deci este nevoie de calculul direct pentru stabilirea stabilitatii, lucru care se poate face si cu ajutorul unui calculator.
Enunt : Fie matricea de dimensiune n × n :
![]()
Un sistem liniar si stationar este asiptotic stabil atunci si numai atunci cand este indeplinita una din conditiile :
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. 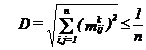
Demonstratie : Pentru un sistem stabil trebuie ca radacinile sau valorile proprii λi ale ecuatiei caracteristice │λ ∙ I - A│ = 0 sa aiba partea reala negativa, deci trebuie sa fie localizate semiplanul stang al planului complex :
![]()
Semiplanul se poate transforma intr-un cerc de raza unitara cu centrul in origine cu ajutorul transformarii omografice :
![]()
Ecuatia caracteristica devine :
![]()
iar dupa cateva transformari obtinem relatia :
![]()
unde :
![]()
In acest caz sistemul va fi stabil daca toate radacinile pi sunt subunitare (pi < 1), lucru care este adevarat cand elementele matricei M tind la zero odata cu ridicarea la putere a acesteia; este tocmai prima conditie. Conditia a doua este o metoda de verificare a convergentelor elementelor, iar ultimele trei conditii sunt de verificare a convergentelor prin calcul a normelor matricei Mk.
3.6. Criteriul de stabilitate logaritmic sau criteriul Bode
Condiția necesara și
suficienta ca un sistem de reglare sa fie asimptotic stabil este ca
graficul defazajului sa intersecteze axa defazajului j p intr-un punct ![]() situat dupa intersecția cu axa lgw a
grafului atenuarii. Daca cele 2 puncte coincid sistemul este limitat
stabil iar in rest sistemul este instabil.
situat dupa intersecția cu axa lgw a
grafului atenuarii. Daca cele 2 puncte coincid sistemul este limitat
stabil iar in rest sistemul este instabil.
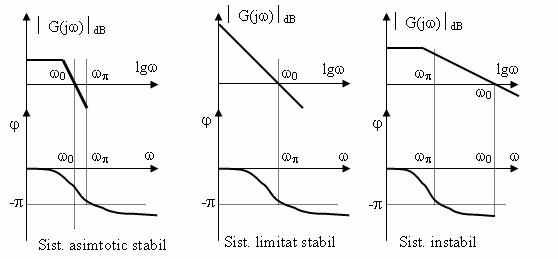
Fig.10
Se stie ca atunci cand funcția de
transfer ![]() a unui sistem inchis are poli pe axa
imaginara sistemul se afla la limita de stabilitate, aceasta se
traduce prin trecerea locului de transfer a sistemului deschis
a unui sistem inchis are poli pe axa
imaginara sistemul se afla la limita de stabilitate, aceasta se
traduce prin trecerea locului de transfer a sistemului deschis ![]() prin punctul critic
prin punctul critic ![]() la o pulsație particulara
la o pulsație particulara ![]() numita
pulsație critica.
numita
pulsație critica.
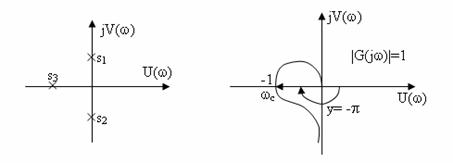
Fig.11
In acest caz raspunsul produs de un impuls la intrarea sistemului ar cuprinde o parte exponențiala corespunzatoare polilor din semiplanul stang și o componenta sinusoidala neamortizata corespunzatoare perechii de poli pur imaginari.
Perechea de poli s1 s2 care sunt cel mai in drepta și cei mai apropiati de axa imaginara ne da efectul dominant in forma marimii de ieșire a sistemului, de aceea acești poli se numesc poli dominanți. Dupa distanța polilor dominanți la axa imaginara se poate aprecia gradul de stabilitate sau stabilitate relativa a sistemului.
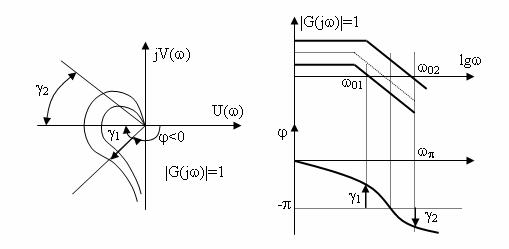
Fig.12
Se numește margine de faza unghiul masurat in punctul de intersecție
dintre locul de transfer al sistemului deschis și cercul de raza
unitate deci unghiul pe care-l face vectorul ![]() corespunzator intersecției cu cercul
unitate care trece prin punctul critic.
corespunzator intersecției cu cercul
unitate care trece prin punctul critic.
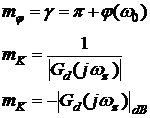
Performantele impuse in cadrul proiectarii SRA se pot referi fie la regimul dinamic fie la regimul stationar fie la caracteristica de frecventa adica la regimul stationar sinusoidal. Performantele stationare si tranzitorii (dinamice) ale SRA sunt:
eroarea stationara
suprareglajul
gradul de amorsare
durata regimului tranzitoriu
timpul de crestere
timpul atingerii primului maxim
timpul atingerii primei valori stationare
pulsatia proprie
stabilitatea sistemelor
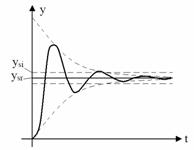
Eroarea stationara est este definita ca diferenta dintre marimea de iesire stationara impusa sau ideala ysi si marimea de iesire stationara reala ysr pentru o marime de intrare trepta unitara :
est = ysi - ysr
Performanta
impusa erorii stationare este de forma ![]() unde valoarea impusa
este valoarea maxima admisibila a erorii stationare. De multe ori se impune ca
eroarea stationara sa fie nula
unde valoarea impusa
este valoarea maxima admisibila a erorii stationare. De multe ori se impune ca
eroarea stationara sa fie nula ![]() . Sistemele la care eroarea stationara este nula sunt sisteme
astatice iar cele la care
. Sistemele la care eroarea stationara este nula sunt sisteme
astatice iar cele la care ![]() sunt sisteme statice.
sunt sisteme statice.
Aplicand teorema
valorii finale din calculul operational ![]() se obtine :
se obtine :
![]()
Consideram cazul unui SRA ce are atat pe calea directa cat si pe calea de reactie functii de transfer strict proprii si fara poli in origine atunci eroarea sistemului este tocmai marimea de iesire din elementul de comparatie EC.
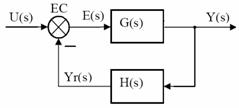
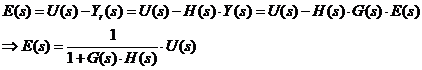
de unde rezulta :
![]()
unde ![]() - coeficientii de transfer de pe calea directa respective pe
calea de reactie
- coeficientii de transfer de pe calea directa respective pe
calea de reactie
![]() - coeficient de
transfer a circuitului deschis
- coeficient de
transfer a circuitului deschis
Se observa ca
astfel de sisteme au eroarea stationara diferita de 0 si sunt sisteme statice.
Pentru asigurarea calitatilor impuse sistemului trebuie ca ![]()
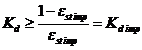
Daca functia de transfer de pe calea de reactie are cel putin un pol in origine :
![]()
rezulta :
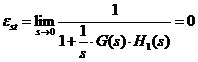
Suprareglarea
Suprareglajul sau suprareglarea
este un indice de calitate al regimului tranzitoriu al SRA provocat de o variatie
a marimii de intrare si se defineste ca fiind depasirea maxima de catre marimea
de iesire ![]() a valorii stationare
a valorii stationare ![]() , valoare care se stabileste dupa trecerea regimului
tranzitoriu :
, valoare care se stabileste dupa trecerea regimului
tranzitoriu :
![]()
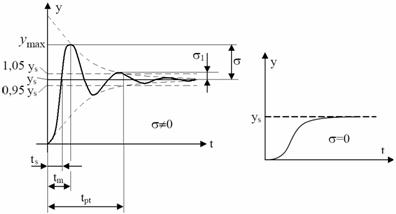
Din al doilea grafic se observa ca daca regimul tranzitoriu este aperiodic atunci suprareglajul este nul. De regula suprareglarea se exprima in procente
![]()
Gradul de amortizare
Gradul de amortizare x este de asemenea un indice de calitate al regimului tranzitoriu si se defineste ca fiind diferenta raportata dintre doua semioscilatii succesive de acelasi sens masurat fata de valoarea stationara.
![]()
Cu cat gradul de amortizare este mai mare cu atat amortizarea oscilatiilor din timpul regimului tranzitoriu este mai rapida ca urmare regimul tranzitoriu este de mai buna calitate.
Durata procesului tranzitoriu
Durata
regimului tranzitoriu este timpul masurat de la inceputul regimului tranzitoriu
pana cand marimea de iesire intra si ramane intr-o banda de latime de 5% de o
parte si de alta a valorii stationare, adica pana cand ![]() . Pentru ca procesul sa fie cat mai bun trebuie ca durata
procesului tranzitoriu sa fie mai mica decat o valoare maxima
. Pentru ca procesul sa fie cat mai bun trebuie ca durata
procesului tranzitoriu sa fie mai mica decat o valoare maxima ![]() .
.
Timpul primei atingeri stationare
Timpul primei
atingeri stationare ![]() este timpul parcurs de la inceputul
regimului tranzitoriu si pana la prima atingere a valorii stationare
este timpul parcurs de la inceputul
regimului tranzitoriu si pana la prima atingere a valorii stationare ![]() .
.
Timpul de crestere
Timpul de
crestere ![]() este durata necesara
variatiei marimii de iesire de la 5% pana la 95% din valoarea stationara
este durata necesara
variatiei marimii de iesire de la 5% pana la 95% din valoarea stationara ![]() .
.
Timpul atingerii primului maxim
Timpul atingerii
primului maxim ![]() este timpul de la
inceputul procesului tranzitoriu pana la atingerea primului maxim.
este timpul de la
inceputul procesului tranzitoriu pana la atingerea primului maxim.
Copyright © 2026 - Toate drepturile rezervate