 | Aeronautica | Comunicatii | Constructii | Electronica | Navigatie | Pompieri |
| Tehnica mecanica |
Schema
echivalenta a retelei monofazate de secventa
homopolara va prezenta fata de inceputul si de
sfarsitul ei doar impedanta ![]() , echivalenta intregii retele. Ea va fi
numita impedanta retelei
monofazate de secventa homopolara, redusa fata de
sectiunea k.
, echivalenta intregii retele. Ea va fi
numita impedanta retelei
monofazate de secventa homopolara, redusa fata de
sectiunea k.
Vom nota scurtcircuitul
simetric sau nesimetric din sectiunea k a sistemului electroenergetic cu simbolul general n.
Rezulta ca n poate fi dupa cum urmeaza:
n = FN; n = 2F; n = 2FN; n = 3F; n = 3FN
Cele trei retele monofazate de secventa ale sistemului electroenergetic din fig.3.26, sunt independente intre ele pentru orice tip n de scurtcircuit care se produce in sectiunea k. Ca urmare, pentru orice tip de scurtcircuit care se produce in sectiunea k a sistemului electroenergetic, teorema a doua a lui Kirchhoff se poate aplica separat pentru fiecare retea in parte. Procedand in acest mod, conform fig.3.26, rezulta:
![]() (3.172)
(3.172)
![]() (3.173)
(3.173)
![]() (3.174)
(3.174)
Tensiunile si
curentii din relatiile de mai sus au urmatoarea
semnificatie: ![]() ,
, ![]() ,
, ![]() , respectiv
, respectiv ![]() ,
, ![]() ,
, ![]() sunt componentele
simetrice ale tensiunii, respectiv ale curentului fazei de referinta
din sectiunea k, adica ale lui
sunt componentele
simetrice ale tensiunii, respectiv ale curentului fazei de referinta
din sectiunea k, adica ale lui ![]() , respectiv
, respectiv ![]() , daca faza r a fost aleasa drept faza de
referinta, (
, daca faza r a fost aleasa drept faza de
referinta, (![]() =
=![]() ;
; ![]() =
=![]() ;
;
![]() =
=![]() ;
; ![]() =
=![]() ;
; ![]() =
=![]() ;
; ![]() =
=![]() ).
).
Daca se considera
cunoscute marimile ![]() ,
, ![]() ,
, ![]() ,
, ![]() , atunci relatiile (3.172),
(3.173), (3.174) sunt trei relatii
independente, care contin sase necunoscute:
, atunci relatiile (3.172),
(3.173), (3.174) sunt trei relatii
independente, care contin sase necunoscute: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Pentru aflarea celor sase necunoscute mai sunt
necesare inca trei relatii independente, care sa
contina cele sase necunoscute. Acestea sunt trei relatii de legatura din timpul scurtcircuitului
intre valorile
. Pentru aflarea celor sase necunoscute mai sunt
necesare inca trei relatii independente, care sa
contina cele sase necunoscute. Acestea sunt trei relatii de legatura din timpul scurtcircuitului
intre valorile ![]() ,
, ![]() ,
, ![]() ale curentilor si valorile
ale curentilor si valorile ![]() ,
, ![]() ,
, ![]() ale tensiunilor din sectiunea k a
sistemului electroenergetic. În fond, ele sunt
trei conditii limita la locul scurtcircuitului si sunt specifice fiecarui tip n de scurtcircuit
simetric sau nesimetric. Ele sunt
cunoscute si sub numele de " cele
trei conditii de functionare ale scurtcircuitului din sectiunea
k".
ale tensiunilor din sectiunea k a
sistemului electroenergetic. În fond, ele sunt
trei conditii limita la locul scurtcircuitului si sunt specifice fiecarui tip n de scurtcircuit
simetric sau nesimetric. Ele sunt
cunoscute si sub numele de " cele
trei conditii de functionare ale scurtcircuitului din sectiunea
k".
În concluzie, fiecare tip n de scurtcircuit, simetric sau nesimetric, din sectiunea k a sistemului electroenergetic este caracterizat prin trei relatii de legatura intre marimile electrice curenti si tensiuni din sectiunea k, numite "conditii limita ale scurtcircuitului din sectiunea k" sau "conditii de functionare ale scurtcircuitului in sectiunea k".
Cele trei
conditii limita ale scurtcircuitului din sectiunea k a
sistemului electro-energetic se pot scrie fie
in componente de faza, fie in componente simetrice. Relatiile
(3.172), (3.173), (3.174), impreuna cu cele trei conditii
limita la locul scurtcircuitului,
scrise in componente simetrice, formeaza un sistem algebric liniar compatibil determinat de sase ecuatii cu sase
necunoscute: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Rezolvand acest sistem se obtin componentele
simetrice de secventa
. Rezolvand acest sistem se obtin componentele
simetrice de secventa ![]() ,
, ![]() ,
, ![]() ale setului trifazat
nesimetric de curenti
ale setului trifazat
nesimetric de curenti ![]() ,
, ![]() ,
, ![]() , respectiv componentele simetrice de secventa
, respectiv componentele simetrice de secventa ![]() ,
, ![]() ,
, ![]() ale setului trifazat
nesimetric de tensiuni
ale setului trifazat
nesimetric de tensiuni ![]() ,
, ![]() ,
, ![]() din sectiunea k.
Din componentele simetrice de secventa
din sectiunea k.
Din componentele simetrice de secventa ![]() ,
, ![]() ,
, ![]() se poate obtine setul trifazat
nesimetric de curenti
se poate obtine setul trifazat
nesimetric de curenti ![]() ,
, ![]() ,
, ![]() , iar din componentele simetrice de secventa
, iar din componentele simetrice de secventa
![]() ,
, ![]() ,
, ![]() se poate obtine setul trifazat nesimetric de tensiuni
se poate obtine setul trifazat nesimetric de tensiuni ![]() ,
, ![]() ,
, ![]() , aplicand matricea
de transformare de la componente simetrice la componente de faza. Astfel:
, aplicand matricea
de transformare de la componente simetrice la componente de faza. Astfel:
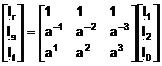 ;
; 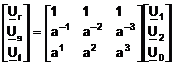 (3.175)
(3.175)
in care matricea de transformare [T]sf de la componente simetrice la componente de faza este:
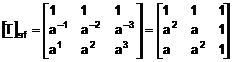 (3.176)
(3.176)
Determinarea componentelor
simetrice ale setului nesimetric de curenti ![]() ,
, ![]() ,
, ![]() , respectiv ale setului trifazat nesimetric de tensiuni
, respectiv ale setului trifazat nesimetric de tensiuni ![]() ,
, ![]() ,
, ![]() din sectiunea k,
in care apare scurtcircuitul,
poate fi abordata si in alt mod. Astfel, cele trei
conditii limita ale unui anumit tip de scurtcircuit din
sectiunea k, scrise in compo-nente
simetrice, permit sa se
stabileasca pentru acel tip de scurtcircuit conexiunile galvanice care trebuie realizate in
sectiunea k intre schemele echivalente ale retelelor monofazate de secventa, reduse fata
de sectiunea k si avand parametrii redusi la un
nivel unic de tensiune. Realizand conexiunile respective se
obtine schema echivalenta
monofazata complexa a tipului respectiv de scurtcircuit. Daca in aceasta schema se
aplica teoremele electrotehnicii, se pot obtine componentele
de secventa ale setului trifazat nesimetric de curenti
din sectiunea k,
in care apare scurtcircuitul,
poate fi abordata si in alt mod. Astfel, cele trei
conditii limita ale unui anumit tip de scurtcircuit din
sectiunea k, scrise in compo-nente
simetrice, permit sa se
stabileasca pentru acel tip de scurtcircuit conexiunile galvanice care trebuie realizate in
sectiunea k intre schemele echivalente ale retelelor monofazate de secventa, reduse fata
de sectiunea k si avand parametrii redusi la un
nivel unic de tensiune. Realizand conexiunile respective se
obtine schema echivalenta
monofazata complexa a tipului respectiv de scurtcircuit. Daca in aceasta schema se
aplica teoremele electrotehnicii, se pot obtine componentele
de secventa ale setului trifazat nesimetric de curenti ![]() ,
, ![]() ,
, ![]() , respectiv compo-nentele
de secventa ale setului trifazat nesimetric de tensiuni
, respectiv compo-nentele
de secventa ale setului trifazat nesimetric de tensiuni ![]() ,
, ![]() ,
, ![]() din sectiunea
k. Din componentele de secventa
gasite se pot obtine respectivele seturi nesimetrice, folosind
relatiile (3.175).
din sectiunea
k. Din componentele de secventa
gasite se pot obtine respectivele seturi nesimetrice, folosind
relatiile (3.175).
Pentru a putea obtine schema echivalenta monofazata complexa a unui tip de scurtcircuit produs in sectiunea k a sistemului electroenergetic este absolut necesar sa se precizeze care este inceputul si care este sfarsitul fiecareia din cele trei scheme echivalente ale retelelor monofazate de secventa ale sistemului, reduse fata de sectiunea k si cu parametrii redusi la un nivel unic de tensiune si care sunt regulile dupa care se intocmesc si se reduc fata de sectiunea k aceste scheme.
Regulile dupa care se intocmesc schemele echivalente ale celor trei retele monofazate de secventa ale unui sistem electroenergetic, reduse fata de sectiunea k in care apare un scurtcircuit simetric sau nesimetric, sunt prezentate in cele ce urmeaza, concomitent cu aplicarea lor pentru exemplul sistemului electroenergetic a carui schema structurala este reprezentata in fig.3.27.a. Se presupune ca in sistemul analizat apare un scurtcircuit simetric sau nesimetric pe bara colectoare E si ca urmare sectiunea k in care apare scurtcircuitul este amplasata pe bara colectoare E.
Schema echivalenta a retelei monofazate de secventa directa a unui sistem electroenergetic este o schema monofazata completa, deoarece contine toate elementele sistemului. Fiecare element este reprezentat prin schema sa echivalenta monofazata de secventa directa, in care intervin parametrii de secventa directa ai elementului. La randul lor, schemele monofazate de secventa directa ale elementelor sistemului se inlantuie in reteaua monofazata de secventa directa a sistemului in aceeasi ordine in care se inlantuie elementele in schema structurala a sistemului.
Schema echivalenta a retelei monofazate de secventa directa a unui sistem electroenergetic contine conductorul de nul, real sau fictiv, numit in continuare si "bara de nul" a retelei monofazate de secventa directa. La bara de nul a schemei echivalente a retelei monofazate de secventa directa se leaga parametrii transversali de secventa directa ai tuturor elementelor sistemului.
Bara de nul a retelei monofazate de secventa directa a unui sistem electro-energetic se obtine unind intre ele toate nulurile elementelor active din sistem (nulul generatoarelor sincrone, nulurile consumatorilor complecsi, nulul gene-ratorului echivalent al sistemului electroenergetic).
Bara de nul a retelei monofazate de secventa directa a sistemului electroenergetic constituie in acelasi timp conductorul de nul pentru fiecare din schemele echivalente monofazate de secventa directa ale elementelor sistemului.
Schema echivalenta a retelei monofazate de secventa directa a unui sistem electroenergetic este o schema activa, deoarece contine tensiunile electromotoare de secventa directa ale elementelor active de retea.
În schema echivalenta a retelei monofazate de secventa directa a sistemului electroenergetic se introduc tensiunile electromotoare de secventa directa ale gene-ratoarelor sincrone, a generatorului echivalent al sistemului, ale consumatorilor com-plecsi si impedantele de secventa directa ale surselor, parametrii de secventa directa longitudinali si transversali ai transformatoarelor, liniilor electrice si consumatorilor.
La efectuarea calculelor de curenti de scurtcircuit, generatoarele sincrone si consumatorul complex se introduc in schema echivalenta a retelei monofazate de secventa directa cu parametrii de secventa directa corespunzatori momentului pentru care se calculeaza regimul tranzitoriu respectiv (de exemplu t=0).
Începutul schemei echivalente a retelei monofazate de secventa directa a unui sistem electroenergetic este locul aparitiei scurtcircuitului din sistem (sec-tiunea k), iar sfarsitul schemei este bara de nul a retelei.
În fig.3.27.b. este reprezentata schema echivalenta a retelei monofazate de secventa directa a sistemului electroenergetic care are schema structurala din fig.3.27.a.
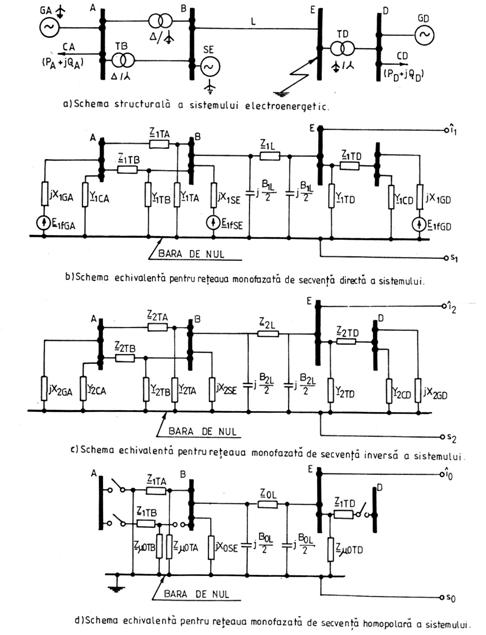
Fig.3.27. Exemplu de intocmire a schemelor echivalente ale retelelor monofazate de secventa ale unui sistem electroenergetic.
Daca in sistemul electroenergetic apare, de exemplu, un scurtcircuit simetric sau nesimetric pe bara E, atunci pentru calculul curentului la scurtcircuitul respectiv, drept inceput i1 al schemei echivalente a retelei monofazate de secventa directa, redusa fata de bara E si avand parametrii redusi la nivel unic de tensiune, se considera chiar bara E, iar drept sfarsit s1 al schemei se considera bara sa de nul (a se vedea fig.3.27.b).
Schema echivalenta a retelei monofazate de secventa inversa a unui sistem electroenergetic este o schema completa, deoarece contine toate elementele sistemului. Fiecare element este reprezentat prin schema sa echivalenta monofazata de secventa inversa, in care intervin parametrii de secventa inversa ai elementului. La randul lor, schemele echivalente monofazate de secventa inversa ale elementelor sistemului se inlantuie in reteaua de secventa inversa a sistemului in aceeasi ordine in care se inlantuie elementele in schema structurala a sistemului. Parametrii transversali de secventa inversa ai elementelor sistemului se leaga la "bara de nul" a schemei echivalente a retelei monofazate de secventa inversa.
Bara de nul a retelei monofazate de secventa inversa a unui sistem electro-energetic se obtine unind intre ele toate nulurile elementelor active din sistem (nulul generatoarelor sincrone, nulurile consumatorilor complecsi, nulul gene-ratorului echivalent al sistemului electroenergetic).
Bara de nul a retelei monofazate de secventa inversa a sistemului electroenergetic constituie in acelasi timp conductorul de nul pentru fiecare din schemele echivalente monofazate de secventa inversa ale elementelor sistemului.
La intocmirea schemei echivalente a retelei monofazate de secventa inversa a unui sistem electroenergetic se va avea in vedere ca:
Ø parametrii de secventa inversa ai elementelor statice de sistem, care sunt elemente cu simetrie totala (transformatoare, autotransformatoare, linii, bobine de reactanta) sunt egali cu cei de secventa directa;
Ø deoarece setul trifazat de tensiuni electromotoare al oricarui element activ de retea este un set trifazat simetric de secventa directa, deci nu contine seturi simetrice de secventa inversa si homopolara, rezulta ca schema echivalenta a retelei monofazate de secventa inversa a sistemului este o schema pasiva;
Ø parametrii de secventa inversa ai elementelor cu simetrie ciclica (generatoare sincrone, consumatori complecsi, motoare electrice) vor fi diferiti fata de cei de secventa directa;
Ø parametrii de secventa inversa ai tuturor elementelor de sistem sunt constanti in perioada oricarui regim tranzitoriu.
Începutul schemei echivalente a retelei monofazate de secventa inversa a unui sistem electroenergetic este locul aparitiei scurtcircuitului din sistem (sectiunea k), iar sfarsitul schemei este bara de nul a retelei.
În fig. 3.27.c. este reprezentata schema echivalenta a retelei monofazate de secventa inversa a sistemului care are schema structurala din fig. 3.27.a. Daca in sistemul electroenergetic apare, de exemplu, un defect nesimetric pe bare E, atunci
pentru calculul regimului respectiv, drept inceput i2 al schemei echivalente a retelei monofazate de secventa inversa, redusa fata de bara E si avand parametrii redusi la nivel unic de tensiune, se considera chiar bara E, iar drept sfarsit s2 al schemei se considera bara sa de nul (a se vedea fig. 3.27.c.)
Schema echivalenta a retelei monofazate de secventa homopolara a unui sistem electroenergetic se intocmeste avandu-se in vedere toate caile posibile de inchidere ale curentilor homopolari. Curentii homopolari, care sunt in faza si strabat cele trei faze ale elementelor de sistem, se intorc la locul nesimetriei fie prin conductorul de nul al retelei, daca acesta exista, fie prin pamant si prin caile paralele cu acesta (firele de garda ale liniilor electrice aeriene, mantalele cablurilor liniilor electrice subterane etc.). Vor exista elemente de sistem care nu sunt parcurse de curentii homopolari si in aceasta situatie schema echivalenta a retelei monofazate de secventa homopolara a sistemului nu va contine acele elemente.
Schema echivalenta a retelei monofazate de secventa homopolara a unui sistem electroenergetic este o schema incompleta, deoarece nu contine schemele echivalente ale acelor elemente de sistem care nu sunt parcurse de curentii homopolari.
Deoarece setul trifazat de tensiuni electromotoare al oricarui element activ de retea este un set trifazat simetric de secventa directa, deci nu contine si set trifazat simetric de secventa homopolara, rezulta ca schema echivalenta a retelei monofazate de secventa homopolora este o schema pasiva.
Spre deosebire de schemele echivalente ale retelelor monofazate de secventa directa si inversa, bara de nul a schemei echivalente a retelei monofazate de secventa homopolara este pamantul sau conductorul fizic de nul, in retelele in care acesta exista.
Începutul schemei echivalente a retelei monofazate de secventa homopolara a unui sistem electroenergetic este locul aparitiei scurtcircuitului nesimetric din sistem (sectiunea k), iar sfarsitul ei este bara de nul a schemei, adica pamantul sau conductorul fizic de nul, in retelele in care acesta exista.
Rolul cel mai important la intocmirea schemei echivalente a retelei monofazate de secventa homopolara a unui sistem electroenergetic il au transformatoarele si autotransformatoarele din sistemul respectiv, deoarece ele stabilesc care din elementele sistemului sunt parcurse de seturi trifazate de curenti de secventa homopolara, cand in sectiunea k a sistemului apare un scurtcircuit nesimetric cu punere la pamant.
În practica, cele mai des folosite scheme echivalente monofazate de secventa homopolara a transformatorului trifazat de forta sunt schema in T (fig.3.28.a) si in Γ (fig.3.28.b.). Asa cum s-a specificat si in paragraful 3.3.4.5, infasurarea primara (p) a transformatorului va fi considerata aceea din infasurarile trifazate ale acestuia in care "intra" setul trifazat de curenti homopolari si infasurarea secundara (s) aceea din infasurarile trifazate ale transformatorului din care "iese" acest set.
Se stie ca parametrii longitudinali din schemele echivalente monofazate de secventa homopolara in T sau in Γ sunt identici cu cei de secventa directa si inversa si deci daca se face referire la schemele din fig.3.28 se poate scrie:
![]() ;
; ![]() (3.177)
(3.177)
![]() (3.178)
(3.178)
![]() (3.179)
(3.179)
![]() (3.180)
(3.180)
unde indicele inferior p a fost atasat parametrilor infasurarii primare, indicele inferior s a fost atasat parametrilor infasurarii secundare, iar indicele superior p arata ca parametrul caruia i-a fost atasat este raportat la infasurarea primara.
De
asemenea se stie ca parametrii transversali ![]() si
si ![]() din schemele
echi-valente monofazate de secventa homopolara in T sau
in Γ, care formeaza impedanta transversala
din schemele
echi-valente monofazate de secventa homopolara in T sau
in Γ, care formeaza impedanta transversala ![]() de magnetizare de
secventa homopolara, sunt complet diferiti de parametrii
transversali de aceeasi natura de secventa directa
si inversa.
de magnetizare de
secventa homopolara, sunt complet diferiti de parametrii
transversali de aceeasi natura de secventa directa
si inversa.
Parametrii din schemele echivalente monofazate de secventa homopolara in T sau in Γ din fig.3.28 corespund situatiei in care ambele infasurari trifazate ale transformatorului sunt parcurse de seturi trifazate de curenti de secventa homopolara.
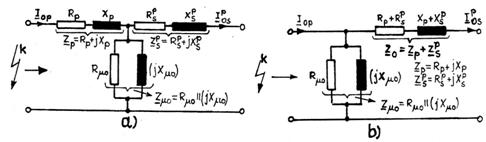
Fig.3.28. Schema echivalenta monofazata de secventa homopolara in T (a) si in Γ (b), pentru transformatorul trifazat de forta, cand infasurarea primara (p) si secundara (s) sunt parcurse de seturi trifazate de curenti homopolari.
În cele ce urmeaza se fac o serie de precizari privind racordarea schemelor echivalente monofazate de secventa homopolara ale transformatoarelor si autotrans-formatoarelor la schema echivalenta a retelei monofazate de secventa homopolara a sistemului electroenergetic, cand intr-o sectiune oarecare k a sistemului apare un scurtcircuit nesimetric cu punere la pamant.
Seturi trifazate de curenti de secventa homopolara apar numai in cazul scurtcircuitelor nesimetrice cu legatura la pamant (FN si 2FN). Cu certitudine ca seturi trifazate de curenti homopolari exista pe fazele zonelor de retea cu nulul legat la pamant si legate galvanic cu sectiunea k, dar astfel de seturi pot sa apara si in alte zone cuplate electromagnetic cu zona retelei care contine sectiunea k.
Pentru a stabili care din elementele sistemului electroenergetic aflate in zonele legate galvanic cu sectiunea k intra cu schemele lor echivalente homopolare in reteaua monofazata de secventa homopolara a sistemului, in sectiunea k a sistemului se aplica un set trifazat de tensiuni homopolare ca in Fig. 3.29. Rezulta seturi trifazate de curenti homopolari care circula dinspre sectiunea k a nesimetriei din sistem spre restul elementelor sistemului. Curentii de secventa homopolara ai celor trei faze sunt in faza si ca urmare au suma diferita de zero in orice nod al sistemului. Din aceasta cauza transformatoarele si autotransformatoarele trifazate din cadrul sistemului electroenergetic sunt "strabatute" de seturi trifazate de curenti homopolari numai daca conexiunile infasurarilor lor permit acest lucru.
În
fig.3.29, din sectiunea k a sistemului electroenergetic, in care
apare un scurtcircuit cu punere la pamant, pleaca spre toate
elementele sistemului seturi trifazate de curenti de secventa
homopolara. Se observa ca unele din elementele sistemului nu pot fi parcurse de seturi trifazate
de curenti de secventa homopolara, ceea ce este
echivalent cu a spune ca acesti curenti au valoarea zero (![]() ;
;![]() ).
).
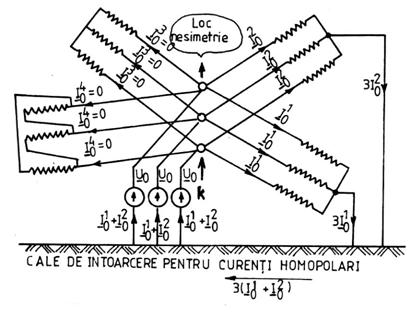
Fig.3.29. Circulatia seturilor trifazate de curenti de secventa homopolara intr-un sistem electroenergetic.
Din cele de mai sus rezulta ca, pentru a exista seturi trifazate de curenti homopolari, trebuie sa existe o cale de intoarcere a acestora la locul nesimetriei din sistemul electroenergetic. Calea de intoarcere a curentilor homopolari ai celor trei faze este constituita fie din pamant, ca in fig.3.29, fie din conductorul fizic de nul al sistemului electroenergetic, daca acest conductor exista. Rezulta ca intr-un transformator trifazat pot "patrunde" curenti homopolari dinspre sectiunea k din sistemul electroenergetic in care apare scurtcircuitul nesimetric cu punere la pamant numai daca acesti curenti vor avea si o cale de "iesire" din transformator. Acest lucru este posibil numai daca transformatorul trifazat are conexiunea in stea sau in zig-zag pentru infasurarea legata galvanic cu sectiunea k a scurtcircuitului nesimetric cu punere la pamant din sistem si are fie neutrul legat la pamant (fig.3.30.a.), fie conductorul fizic de nul (fig.3.30.b.). În aceste cazuri schema echivalenta monofazata de secventa homopolara a transformatorului trifazat se racordeaza la reteaua monofazata de secventa homopolara a partii din sistemul electroenergetic in care a aparut scurtcircuitul nesimetric cu punere la pamant, lucru scos in evidenta cu ajutorul contactorului inchis K din fig.3.30.c
În aceste cazuri, vazut dinspre sectiunea k a
scurtcircuitului nesimetric cu punere la pamant din sistemul electroenergetic,
transformatorul prezinta in raport
cu borna de inceput i0 si de sfarsit s0
ale schemei sale echivalente monofazate de secventa homopolara o
impedanta rezultanta de secventa
homopolara ![]() de valoare finita
(fig.3.30.c.).
de valoare finita
(fig.3.30.c.).
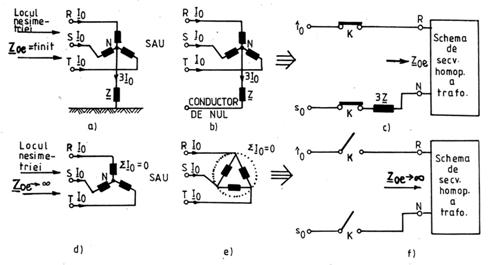
Fig.3.30. Racordarea schemei echivalente monofazate de
secventa homopolara a transformatorului trifazat la reteaua
monofazata de secventa homopolara a sistemului
electroenergetic si impedanta sa echivalenta homopolara ![]() , vazuta dinspre locul scurtcircuitului nesimetric
cu punere la pamant din sistemul electroenergetic.
, vazuta dinspre locul scurtcircuitului nesimetric
cu punere la pamant din sistemul electroenergetic.
Daca conexiunea
infasurarii trifazate a transformatorului, care este
legata galvanic cu sectiunea k a
scurtcircuitului nesimetric cu punere la pamant din sistemul electroenergetic, este in stea fara neutru legat la pamant sau
fara conductor fizic
de nul (fig.3.30.d.) sau in triunghi (fig.3.30.e.), atunci in
transformatorul trifazat nu pot "patrunde"
curenti homopolari dinspre locul scurtcircuitului nesimetric cu punere
la pamant din sistemul electroenergetic, ceea ce este echivalent cu
a spune ca acesti curenti au
valoare zero. Aceasta inseamna ca schema echivalenta de
secventa homopolara a transformatorului trifazat nu se racordeaza la reteaua
monofazata de secventa
homopolara a partii din sistemul electroenergetic in care
a aparut nesimetria cu punere la
pamant, lucru scos in evidenta cu ajutorului
contactorului deschis K din fig.3.30.f.
În aceste cazuri, vazut
dinspre sectiunea k a scurtcircuitului nesimetric cu punere la pamant din
sistemul electroenergetic, transformatorul prezinta in raport cu borna de inceput i0
si de sfarsit s0 ale schemei sale monofazate de secventa homopolara o
impedanta rezultanta de secventa homopolara ![]() de valoare
infinita (fig.3.30.f).
de valoare
infinita (fig.3.30.f).
Daca transformatorul
trifazat are pentru infasurarea primara conexiunea
in stea sau zig-zag cu neutrul legat la pamant sau cu
conductor de nul, atunci calea de intoarcere pentru curentii
homopolari, constituita din pamant sau din conductorul de nul,
este parcursa de suma curentilor homopolari ai celor trei faze,
adica de ![]() . Orice impedanta
. Orice impedanta ![]() , amplasata pe calea de intoarcere a
curentilor homopolari, intre punctul de stea al transformatorului
si sectiunea k a scurtcircuitului nesimetric cu punerea la pamant din sistemul
electroenergetic (fig.3.30.a si fig.3.30.b) este parcursa de suma
, amplasata pe calea de intoarcere a
curentilor homopolari, intre punctul de stea al transformatorului
si sectiunea k a scurtcircuitului nesimetric cu punerea la pamant din sistemul
electroenergetic (fig.3.30.a si fig.3.30.b) este parcursa de suma ![]() a curentilor homopolari ai celor trei faze. Caderea
de tensiune pe aceasta impedanta este:
a curentilor homopolari ai celor trei faze. Caderea
de tensiune pe aceasta impedanta este:
![]() (3.181)
(3.181)
Relatia (3.181) arata
ca o impedanta ![]() de pe calea comuna de intoarcere a curentilor
homopolari este echivalenta cu o impedanta (3
de pe calea comuna de intoarcere a curentilor
homopolari este echivalenta cu o impedanta (3![]() ) introdusa in circuitul unei faze, deoarece o
faza este parcursa numai de curentul
) introdusa in circuitul unei faze, deoarece o
faza este parcursa numai de curentul ![]() . Din aceasta cauza, in schema
echivalenta monofazata de secventa homopolara,
in care sunt reprezentati numai
parametrii de secventa homopolara ai fazei de
referinta si ai caii de nul, adica ai caii de intoarcere a curentilor
homopolari, orice impedanta
. Din aceasta cauza, in schema
echivalenta monofazata de secventa homopolara,
in care sunt reprezentati numai
parametrii de secventa homopolara ai fazei de
referinta si ai caii de nul, adica ai caii de intoarcere a curentilor
homopolari, orice impedanta ![]() de pe calea
comuna de
intoarcere a curentilor homopolari se introduce cu valoarea 3
de pe calea
comuna de
intoarcere a curentilor homopolari se introduce cu valoarea 3![]() (fig.3.30.c)
(fig.3.30.c)
Chiar daca dinspre sectiunea k din sistemul electroenergetic, in care s-a produs scurtcircuitul nesimetric cu punere la pamant, pot patrunde curenti homopolari in infasurarea primara a transformatorului de forta, aceasta infasurare avand conexiunea in stea sau in zig-zag cu neutrul legat la pamant , nu in toate cazurile apar curenti homopolari si in infasurarea sa secundara. Sub acest aspect, in practica se intalnesc cazurile prezentate in tabelul 3.3.
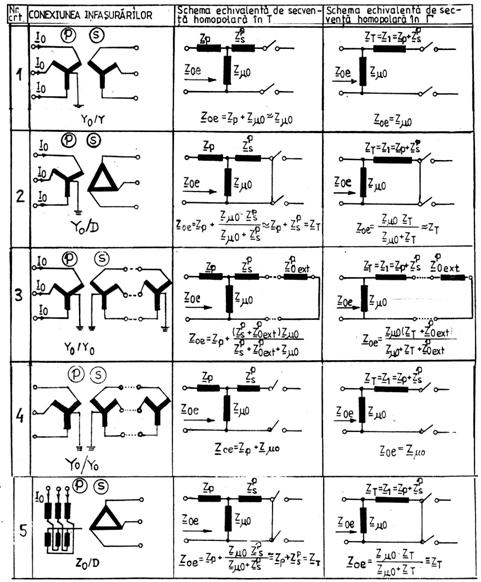
1) Daca infasurarea primara a transformatorului analizat are conexiunea in stea cu neutrul legat la pamant, iar infasurarea sa secundara are conexiunea in stea fara neutru legat la pamant sau fara conductor de nul (nr.crt.1 din tabelul 3.3), atunci in infasurarea secundara nu pot lua nastere curenti homopolari, deci in schema echivalenta monofazata de secventa homopolara a transformatorului secundarul sau trebuie sa fie in gol. Ca urmare, circuitul secundar al schemei echivalente monofazate de secventa homopolara a transformatorului analizat este intrerupt pentru curentii de secventa homopolara, lucru simbolizat in schema prin cele doua contacte deschise, amplasate in secundar. Acest lucru este echivalent cu a spune ca schema echivalenta monofazata de secventa homopolara a transformatorului este decuplata de la
TABELUL 3.3. Racordarea schemelor echivalente monofazate de secventa homopolara a transformatoarelor trifazate cu doua infasurari in schema echivalenta a retelei monofazate de secventa homopolara a sistemului electroenergetic si impedanta lor homopolara echivalenta
schema echivalenta a retelei monofazate de
secventa homopolara a partii sistemului electroenergetic
conectata galvanic in secundarul transformatorului de
forta analizat. Impedanta echivalenta de secventa
homopolara ![]() a
transfor-matorului trifazat analizat, vazuta dinspre sectiunea k
a sistemului electroenergetic in care
apare scurtcircuitul nesimetric cu punere la pamant, va fi mult mai
mare decat impedanta sa longitudinala
a
transfor-matorului trifazat analizat, vazuta dinspre sectiunea k
a sistemului electroenergetic in care
apare scurtcircuitul nesimetric cu punere la pamant, va fi mult mai
mare decat impedanta sa longitudinala ![]() de secventa homopolara. Expresia ei de
calcul este:
de secventa homopolara. Expresia ei de
calcul este:
pentru schema echivalenta monofazata in T:
![]() (3.182)
(3.182)
pentru schema echivalenta monofazata in Γ, cu ramura transversala spre primar:
![]() (3.183)
(3.183)
2) Daca
infasurarea primara a transformatorului analizat are
conexiunea in stea cu neutrul legat la
pamant, iar infasurarea sa secundara are conexiunea
in triunghi (nr. crt. 2 din
tabelul 3.3), atunci infasurarea secundara este
parcursa de curenti homopolari, dar acestia nu pot
parasi transformatorul. Într-adevar, tensiunile
elec-tromotoare de secventa homopolara induse in cele trei
faze secundare conectate in triunghi sunt in faza si
stabilesc in cele trei faze curenti homopolari, care se inchid
pe bucla de retea formata din triunghiul
infasurarii secundare. Valoarea acestor curenti este
limitata numai de impedanta infasurarii
secundare. Transformatorul se comporta ca in regim de scurtcircuit,
iar infasurarea sa secundara poate fi asimilata cu o spira in scurtcircuit pentru
curentii homopolari. Acest lucru se simuleaza prin scurtcircuitarea infasurarii secundare in
schema echivalenta monofazata de secventa homopolara a
transformatorului. În plus, curentii homopolari din secundar nu pot
parasi transformatorul, deoarece pentru ei nu exista cale de
intoarcere in reteaua conectata in secundarul
transformatorului. De aceea, transformatorul avand conexiunile
infasurarilor: primara = stea cu neutrul legat la
pamant / secundara = triunghi, reprezinta un element terminal pentru reteaua
monofazata de secventa homopolara, iar schema sa echivalenta monofazata de secventa
homopolara trebuie deconectata
fata de schema echivalenta a retelei monofazate de
secventa homopolara din secundarul sau. Acest
lucru s-a simulat in schema prin cele doua contacte deschise , amplasate in secundar.
Impedanta echivalenta de secventa homopolara ![]() a transformatorului analizat,
vazuta dinspre sectiunea k a sistemului electroenergetic
in care apare scurtcircuitul nesimetric cu punere la pamant,
va avea valoarea foarte apropiata de valoarea impedantei
longitudinale de secventa directa a transformatorului, care,
dupa cum se stie, este egala cu impedanta
longitudinala de secventa homopolara. Expresia ei de calcul
este:
a transformatorului analizat,
vazuta dinspre sectiunea k a sistemului electroenergetic
in care apare scurtcircuitul nesimetric cu punere la pamant,
va avea valoarea foarte apropiata de valoarea impedantei
longitudinale de secventa directa a transformatorului, care,
dupa cum se stie, este egala cu impedanta
longitudinala de secventa homopolara. Expresia ei de calcul
este:
pentru schema echivalenta monofazata in T:
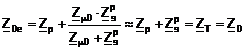 (3.184)
(3.184)
pentru schema echivalenta monofazata in Γ, cu ramura transversala spre primar:
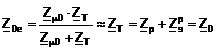 (3.185)
(3.185)
Daca se are in
vedere faptul ca impedanta de magnetizare de secventa
homo-polara ![]() are valoarea mult mai
mare decat
are valoarea mult mai
mare decat ![]()
![]() , respectiv decat
, respectiv decat ![]()
![]() si daca la
numitorul fractiilor din relatiile (3.184), respectiv (3.185), se
neglijeaza
si daca la
numitorul fractiilor din relatiile (3.184), respectiv (3.185), se
neglijeaza ![]() , respectiv
, respectiv ![]() , fata de
, fata de ![]() , atunci rezulta valoarea aproximativa a lui
, atunci rezulta valoarea aproximativa a lui ![]() , data de relatiile (3.184), respectiv (3.185).
, data de relatiile (3.184), respectiv (3.185).
3) Daca
infasurarea primara a transformatorului analizat are
conexiunea stea cu neutrul legat la
pamant, iar infasurarea sa secundara are
conexiunea tot stea cu neutrul legat
la pamant (nr.crt.3 si nr. crt.4 din tabelul 3.3), atunci
in infasurarea secundara pot apare
curenti homopolari numai daca in reteaua legata
galvanic cu ea mai exista cel putin un transformator cu neutrul
infasurarii dinspre transformatorul analizat legat la pamant, care sa
asigure o cale de intoarcere prin pamant pentru acesti
curenti homopolari (nr.crt.3 din tabelul 3.3) În aceasta
situatie schema echivalenta monofazata de secventa
homopolara a transformatorului analizat se leaga galvanic cu impedanta echivalenta de
secventa homopolara ![]() a elementelor din
reteaua secundara care sunt parcurse de curenti homopolari. De
aceea, in acest caz nu se poate vorbi
de o impedanta proprie echivalenta de secventa
homopolara
a elementelor din
reteaua secundara care sunt parcurse de curenti homopolari. De
aceea, in acest caz nu se poate vorbi
de o impedanta proprie echivalenta de secventa
homopolara ![]() a transformatorului analizat, vazuta dinspre
sectiunea k din sistemul electroenergetic, in care apare
scurtcircuitul nesimetric cu punere la pamant. Dinspre
sectiunea k in care apare scurtcircuitul nesimetric cu punere la
pamant "se vede" o impedanta echivalenta care contine atat parametrii de
secventa homopolara ai transformatorului analizat,
cat si impedanta homopolara
a transformatorului analizat, vazuta dinspre
sectiunea k din sistemul electroenergetic, in care apare
scurtcircuitul nesimetric cu punere la pamant. Dinspre
sectiunea k in care apare scurtcircuitul nesimetric cu punere la
pamant "se vede" o impedanta echivalenta care contine atat parametrii de
secventa homopolara ai transformatorului analizat,
cat si impedanta homopolara ![]() a elementelor
conectate in secundarul sau. În raport cu bornele primarului,
aceasta impedanta echivalenta are expresia:
a elementelor
conectate in secundarul sau. În raport cu bornele primarului,
aceasta impedanta echivalenta are expresia:
Ø pentru schema echivalenta monofazata in T:
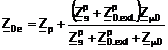 (3.186.a)
(3.186.a)
Ø pentru schema echivalenta monofazata in G, cu ramura transversala spre primar:
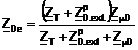 (3.186.b)
(3.186.b)
Daca in reteaua
legata galvanic cu secundarul transformatorului analizat nu exista nici un alt transformator cu neutrul
infasurarii dinspre transformatorul analizat legat
la pamant (nr.crt.4 din tabelul 3.3), atunci in
infasurarea secundara a transfor-matorului analizat nu se
pot stabili curenti homopolari, deoarece pentru ei nu exista cale de
intoarcere. În aceasta situatie, secundarul schemei
echivalente de secventa homopolara
a transformatorului analizat, desi are conexiunea in stea cu neutrul
legat la pamant, se decupleaza fata de restul
retelei monofazate de secventa homopolara. În concluzie, desi ambele
infasurari ale transformatorului analizat au conexiunea
in stea cu neutrul legat la pamant, transformatorul se
comporta fata de setul trifazat de curenti homopolari care "intra" in primar ca un
transformator a carui infasurare primara are
conexiunea in stea cu neutrul legat la pamant si a
carui infasurare secundara are conexiunea in
stea cu neutrul nelegat la pamant. Impedanta echivalenta
de secventa homopolara ![]() a transformatorului analizat, vazuta dinspre
sectiunea k din sistemul electroenergetic, in care se produce
un scurtcircuit nesimetric cu punere la pamant, va fi de valoare
foarte mare. Expresia ei de calcul este:
a transformatorului analizat, vazuta dinspre
sectiunea k din sistemul electroenergetic, in care se produce
un scurtcircuit nesimetric cu punere la pamant, va fi de valoare
foarte mare. Expresia ei de calcul este:
pentru schema echivalenta monofazata in T:
![]() (3.187)
(3.187)
pentru schema echivalenta monofazata in Γ cu ramura transversala spre primar:
![]() (3.188)
(3.188)
4) Daca infasurarea primara a transformatorului analizat are conexiunea in zig-zag cu neutrul legat la pamant (nr.crt.5 din tabelul 3.3), atunci el se comporta fata de setul trifazat de curenti homopolari care "intra" in infasurarea primara in mod identic cu un transformator a carui infasurare primara are conexiunea in stea cu neutrul legat la pamant si a carui infasurare secundara are aceeasi conexiune cu cea a infasurarii secundare a transformatorului analizat.
Un transformator trifazat cu trei infasurari (primara, secundara, tertiara) se comporta fata de un set trifazat de curenti homopolari, care "intra" in infasurarea sa primara, conform principiilor prezentate pentru transformatorul cu doua infasurari. Se considera infasurare primara a transformatorului cu trei infasurari, acea infasurare care este legata galvanic cu sectiunea k din sistemul electroenergetic, in care se produce scurtcircuitul nesimetric cu punere la pamant. Setul trifazat de curenti homopolari poate "intra", dinspre sectiunea k , in transformatorul cu trei infasurari, numai daca infasurarea sa primara are conexiunea in stea sau in zig-zag cu neutrul legat la pamant, deoarece numai in acest caz se asigura cale de intoarcere pentru curentii homopolari intrati in transformator. Daca infasurarea primara a transformatorului cu trei infasurari are conexiunea in stea cu neutrul izolat sau in triunghi, atunci setul trifazat de curenti homopolari dinspre sectiunea k nu poate "intra" in infasurarea sa primara si schema echivalenta monofazata de secventa homopolara a transformatorului cu trei infasurari se decupleaza in intregime dinspre primar de la schema echivalenta a retelei monofazate de secventa homopolara a sistemului electroenergetic.
Daca
infasurarea primara a transformatorului cu trei
infasurari are conexiunea in stea sau in zig-zag cu neutrul legat la pamant,
atunci setul trifazat de curenti homopolari care vine dinspre
sectiunea k poate "intra" in transformatorul cu trei infasurari. În
aceasta situatie, modul de racordare a schemei echivalente monofazate
de secventa homopolara a transformatorului cu trei
infasurari in schema echivalenta a retelei
monofazate de secventa homopolara a sistemului electroenergetic,
depinde de tipul conexiunii infasurarii sale secundare
si de tipul conexiunii infasurarii sale tertiare. În tabelul 3.4 este indicat
acest mod de racordare precum si expresia impedantei
echivalente de secventa homopolara ![]() a transformatorului cu
trei infasurari,
vazuta dinspre sectiunea k , pentru tipurile uzuale de conexiuni
ale infasurarii secundare, respectiv tertiare.
a transformatorului cu
trei infasurari,
vazuta dinspre sectiunea k , pentru tipurile uzuale de conexiuni
ale infasurarii secundare, respectiv tertiare.
TABELUL 3.4. Racordarea schemei echivalente monofazate de secventa homopolara a transformatorului cu trei infasurari in schema echivalenta a retelei monofazate de secventa homopolara a sistemului electroenergetic si impedanta lui homopolara echivalenta.
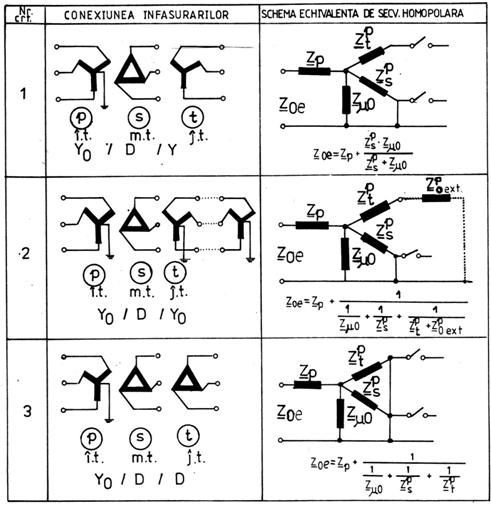
În ceea ce priveste modul de racordare a schemei echivalente monofazate de secventa homopolara a unui autotransformator in schema echivalenta a retelei monofazate de secventa homopolara a sistemului electroenergetic, apar anumite particularitati, deoarece intre infasurarile autotransformatorului exista, pe langa cuplajul magnetic, si o legatura galvanica. În tabelul 3.5 sunt indicate, ca exemple, modurile de racordare ale schemelor echivalente monofazate de secventa homopolara ale autotransformatoarelor cu infasurarea tertiara avand conexiunea in triunghi, in schema echivalenta a retelei monofazate de secventa homopolara a sistemului electroenergetic.
TABELUL 3.5. Racordarea schemei echivalente monofazate de secventa homopolara a autotransformatorului avand infasurare tertiara cu conexiunea in triunghi, in schema echivalenta a retelei monofazate de secventa homopolara a sistemului electroenergetic si impedanta lui homopolara echivalenta.
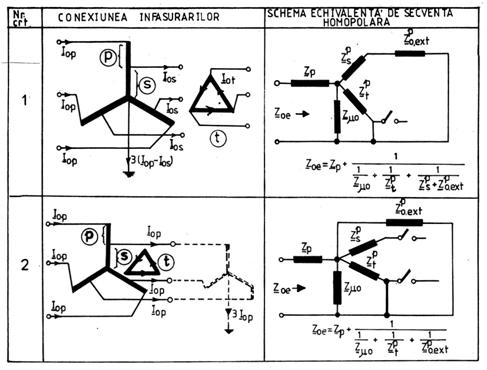
O analiza a acestor situatii conduce la urmatoarele concluzii:
daca neutrul autotransformatorului este legat la pamant (nr.crt. 1 din tabelul 3.5), atunci racordarea schemei sale echivalente de secventa homopolara in schema echivalenta a retelei monofazate de secventa homopolara a sistemului electro-energetic este identica cu racordarea schemei echivalente monofazate de secventa homopolara a unui transformator cu trei infasurari cu aceleasi conexiuni pentru infasurarea primara, secundara si tertiara;
Copyright © 2025 - Toate drepturile rezervate