Analiza circuitelor liniare in regim periodic permanent si nesinusoidal

Analiza circuitelor liniare in regim periodic permanent si nesinusoidal

Fiind dati parametrii circuitului si tensiunile nesinusoidale aplicate la borne, se cer curentii care se stabilesc in fiecare latura din circuit. Descompunand t.e.m. nesinusoidale (cu ajutorul seriei Fourier) in componenta continua si armonice (componente sinusoidale) se reduce studiul regimului periodic nesinusoidal la:

a)     studiul unui regim de curent continuu (pentru componenta continua);

b)     studiul     unor regimuri sinusoidale (pentru fiecare armonica de pulsatie k in parte

Se determina pentru curentii din fiecare latura componenta continua si armonicele

iar prin suprapunerea lor se obtine valoarea instantanee a curentilor din laturi.

In analiza circuitului, se poate utiliza reprezentarea in complex pentru fiecare armonica, observand ca la frecventa a armonicei k, reactantele condensatoarelor vor fi de k ori mai mici, iar ale bobinelor de k ori mai mari decat fundamentala:

(39)

Pentru fiecare armonica, studiul se poate face cu metodele de analiza cunoscute de la regimul permanent sinusoidal.

1. Rezistorul ideal in regim nesinusoidal (fig. 10,a)

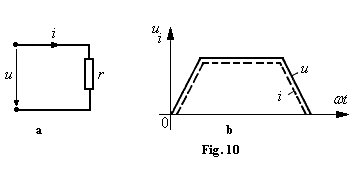La bornele unui rezistor ideal r e aplicata o tensiune periodica nesinusoidala u, cu dezvoltarea in serie:   

Scriind legea lui Ohm pentru fiecare componenta in parte (continua si armonice), rezulta: (40)

O rezistenta pura nu modifica forma curentului fata de cea a tensiunii (unda lui i este asemenea cu unda lui u, fig. 10,b.

Factorul de distorsiune al curentului este egal cu factorul de distorsiune al tensiunii:

2. Bobina ideala in regim nesinusoidal (fig. 11,a)

La bornele bobinei se aplica o tensiune nesinusoidala:   

Curentul ce se stabileste in circuit in regim permanent este:

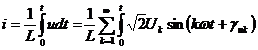
Efectuand integrarea, rezulta curentul instantaneu:

₍₄₁₎

unde : (42)

Valorile efective ale armonicelor sunt:    (43)

O inductivitate reduce distorsiu-nea curentului fata de distorsiunea ten-siunii, deoarece prezinta o impedanta proportionala cu ordinul armonicei. La bobine factorul de distorsiune al curentului este mai mic decat factorul de distorsiune al tensiunii (). In figura 11,b se prezinta tensiunea u si curentul i printr-o bobina ideala.

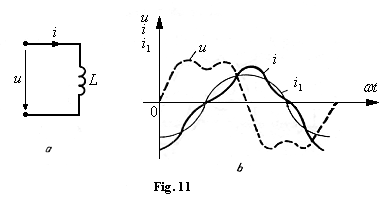
3. Condensatorul ideal in regim nesinusoidal (fig. 12,a)

La bornele condensatorului se aplica o tensiune nesinusoidala   

Curentul ce se stabileste in circuit este:

sau: (44)

unde: (45)

Valorile efective ale armonicelor sunt:

(46)

O capacitate accentueaza deformarea curentului fata de distorsiunea tensiunii, deoarece impedanta scade cu ordinul armonicei. In figura 12,b se da forma de unda a tensiunii si curentului printr-un condensator.

La condensatoare, factorul de distorsiune al curentului e mai mare decat factorul de distorsiune al tensiunii ().

4. Circuitul R, L, C in regim nesinusoidal

Circuitul fiind liniar, se aplica teorema superpozitiei. Se considera ca in circuit fiecare armonica de tensiune u_k actioneaza separat si da nastere unei armonice de curent i_k. Curentul instantaneu din circuit se obtine din insumarea armonicelor curentului:

Impedanta armonicei de ordin k are expresia: 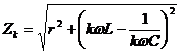(47)

Valoarea efectiva a curentului de armonica k este: (48)

Reactanta inductiva si capacitiva corespunzatoare armonicei k variaza in mod diferit cu frecventa: reactanta inductiva creste, iar cea capacitiva scade cu ordinul armonicei:

(49)

Aplicatii

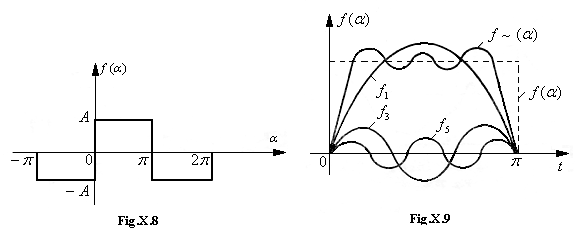
Dezvoltarea in serie Fourier a unei unde dreptunghiulare cunoscuta analitic (fig. 7). Fie un semnal dreptunghiular de amplitudine A avand exprimarea analitica:

Functia fiind alternativ simetrica impara va contine numai armonice impare

in sinus :

Intr-adevar, cu relatiile (X.7) avem: 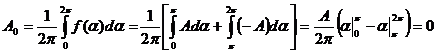(X.13)

apoi:

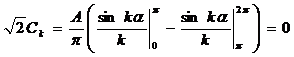(X.14)

si, in fine:

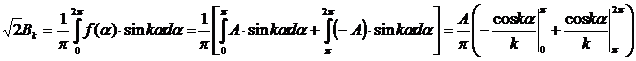a) Daca :

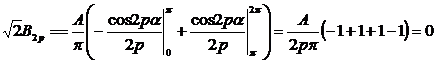
in serie nu apar armonice pare in sinus: .

b) Daca :

(X.15)

Relatiile (X.13), (X.14) si (X.15) introduse in (X.6) ne dau seria: (X.16)

sau dezvoltat si revenind la notatia :

(X.17)

Cu cat se considera mai multe armonice, cu atat se obtine o curba mai apropiata de un dreptunghi. Daca aproximam functia prin suma primilor trei termeni, se obtine:

cu reprezentarea grafica din figura X.8.

Exemplu

Sa se traseze spectrul de amplitudine pentru un semnal dreptunghiular de amplitudine A (fig. X.10). Seria Fourier a semnalului contine numai armonice impare in sinus (relatia X.17). Ne limitam la armonica a saptea:

Sa scriem amplitudinile armonicelor:

Deci: . Pentru seria (X.17) amplitudinile armonicelor sunt:

Cu aceste valori, s-a trasat spectrul de amplitudine al semnalului (X.17) in figura X.11.

Aplicatie

Sa determinam coeficientul de distorsiune pentru o unda dreptunghiulara de amplitudine A, care are serie Fourier (X.17).

Componenta continua e nula , iar valoarea efectiva este data de:

Reziduul deformant este deci:

Coeficientul de distorsiune devine: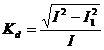

unde:

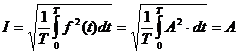si

Inlocuind valorile, se obtine :

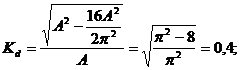
(X.32)

In regim sinusoidal, coeficientul de distorsiune este nul ().

Aplicatie

Sa se calculeze puterile P, Q, S, D. considerand un circuit dipolar la bornele caruia se aplica o tensiune sinusoidala U=U₁, ce da nastere unui curent nesinusoidal:

Puterea activa P este :

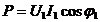
Puterea reactiva Q este :

Puterea aparenta S se calculeaza din:

Sa separam in expresia lui S cele trei componente P, Q si D:

Puterea deformanta D rezulta deci: