Note de calcul referitoare la verificarea stabilitatii taluzului adiacent danei

Note de calcul referitoare la verificarea stabilitatii taluzului adiacent danei.

Prin taluz se intelege o suprafata inclinata care margineste un rambleu sau un debleu. Taluzul poate fi de provenienta naturala sau artificiala. O problema importanta in practica este aprecierea gradului de stabilitate a taluzurilor si dimensionarea lor in asa fel incat ele sa nu-si piarda stabilitatea pe tot timpul existentei lor. Hotaratoare in asigurarea stabilitatii taluzului sunt inclinarea pe care o are fata de planul orizontal si si forma sa.

Sub actiunea fortelor, in taluz apare o stare de tensiuni a caror marime este functie de aceste forte si in momentul in care intr-un punct aceste tensiuni depasesc rezistenta materialului din care este alcatuit taluzul, apare aici o rupere prin alunecare.

Fortele care actioneaza asupra taluzurilor sunt: forta gravitationala, antrenarea hidrodinamica, cutremurele de pamant si supraincarcarile care se aplica la suprafata sa. Forta gravitatiei este functie de greutatea volumica a pamantului si depinde de toti factorii care influenteaza marimea acestei greutati. Rezistenta pamnatului din care este alcatuit taluzul este determinata de indicii rezistentei sale la forfecare.

Suprafata pe care are loc deplasarea se numeste "suprafata de alunecare". In realitate ea nu este o suprafata ci o zona de o anumita grosime. In practica sa constatat ca suprafata poate fi aproximata cu o suprafata cilindrica, avand ca directoare o curba oarecare. Forma acestei suprafete depinde foarte mult de gradul de omogenitate al taluzului.

Pentru verificarea stabilitatii unui taluz se pot aborda doua cai:

rezolvarea teoretica a problemei, pornind de la ecuatiile de echilibru-limita si conditiile de contur specifice problemei analizate;

un studiu static al echilibrului general al masivului, presupunand in mod anticipat o anumita forma pentru directoarea suprafetei de alunecare, denumita curent linie de alunecare, care se presupune ca se produce instantaneu in toata masa de pamant.

Prima cale da solutii exacte insa poate fi aplicata numai la un masiv omogen si izotrop. Calea a doua poate fi aplicata in conditii foarte variate, deoarece in cadrul ei se poate tine seama de stratificatia din taluz, de diferitele sarcini exterioare care actioneaza asupra taluzului, de actiunea hidrodinamica a apei si de sarcinile seismice.

Linia de alunecare este un cerc. Bazat pe observatia ca suprafata de alunecare la pamanturile argiloase se apropie foarte mult de o suprafata cilindrica circulara, s-au elaborat o serie de metode care presupun o linie de alunecare sub forma unui cerc.

Aceste metode pot fi impartite in doua grupe:

metode care considera echilibrul unor volume elementare verticale luate in ansamblu;

metode care considera echilibrul intregului masiv care lucreaza ca un tot.

Procedeul de trasare al fasiilor:

se prelungesc dreptele directoare ale unghiurilor si ce se vor intersecta in punctul O;

prin punctul O se costruieste arcul de cerc avand centrul in O si raza OB, pana intersecteaza cota NA;

din punctul O se duce prima verticala, ce va delimita zona in care unghiurile sunt pozitive, respectiv negative;

se duce a doua verticala prin punctul A;

prin punctele de intersectie dintre suprafata de alunecare si linia de separatie a doua straturi adiacente se duc verticale (in zonele obtinute intre doua verticale consecutive fasiile se vor sprijini pe acelasi strat);

se duc fasiile avand baza de cel mult 1m, rotunjite, atunci cand este cazul la 0,1 sau 0,2 m;

se construiesc corzile ce subantind arcele aferente fiecarei fasii;

se construieste prin mijlocul fiecarei fasii, dreapta pe care se va masura inaltimea fiecarui strat parcurs de acea fasie;

se uneste centrul O cu intersectia dintre coarda si inaltimea aferente fiecarei fasii in parte rezultand intre aceasta dreapta si verticala ce trece prin O unghiul aferent fiecarei fasii.

In cadrul primei grupe masivul se imparte in fasii verticale suficient de inguste ca sa se poata considera ca impingerile pe peretii verticali ai fasiilor se echilibreaza reciproc. In mod curent numerotarea fasiilor se face din amonte spre aval. In cazul in care la extremitatea amonte exista o fasie situata numai in apa aceasta poate capata numarul de ordine "0". Prima fasie se noteaza cu 1, inaltimea ei determinandu-se din adancimea fisurii care poata sa apara la partea superioara a versantului. Ea se poate calcula cu relatia:

(1)

Cercul de rupere se duce in mod arbitrar prin partea de jos a crapaturii.

Greutatea G a fasiei este echilibrata de reactiunea terenului.

Fortele care asigura stabilitatea unei fasii sunt C si Ff (coeziunea care se dezvolta pe suprafata de alunecare de la baza fasiei i frecarea de pe aceeasi suprafata). Forta care provoaca deplasarea fasiei este componenta tangentiala a greutatii fasiei T.

Se defineste drept grad de siguranta la alunecare a taluzului dupa cercul cosiderat raportul dintre momentul fortelor care asigura stabilitatea masivului asezat deasupra suprafetei de alunecare si momentul fortelor care produc alunecarea lui. Momentele se iau fata de centrul O al cercului de alunecare. Explicitand valorile fortelor si luand in considerare echilibrul intregului ansamblu de fasii se obtine expresia:

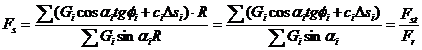(2)

In care:

factor de siguranta

forta de stabilitate

forta de rasturnare

Gi - este greutatea fasiei i;

αi - unghiul dintre verticala prin centrul O si normala la cerc care trece prin mijlocul bazei fasiei i;

ci - coeziunea pamantului la baza fasiei i;

Φi - unghiul de frecare interioara al materialului de la baza fasiei i;

Δsi - lungimea arcului reprezentand baza fasiei i.

Frecarea si coeziunea se presupune ca se repartizeaza uniform pe baza fasiei i.

Daca se noteaza cu h_im inaltimea medie a unei fasii, greutatea ei va avea expresia:

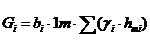(3)

De asemenea, daca se asimileaza arcul de cerc de la baza fasiei cu coarda corespunzatoare se poate scrie:

(4)

si relatia (2) devine:

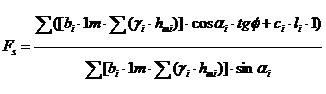(5)

Gradul de siguranta trebuie sa fie minim 1.2. In cazul unui teren neomogen se admite sa se introduca in calcul un unghi de frecare si o coeziune calculate ca medii ponderate, ponderile fiind reprezentate prin lungimile arcelor de alunecare corespunzatoare diferitelor straturi.

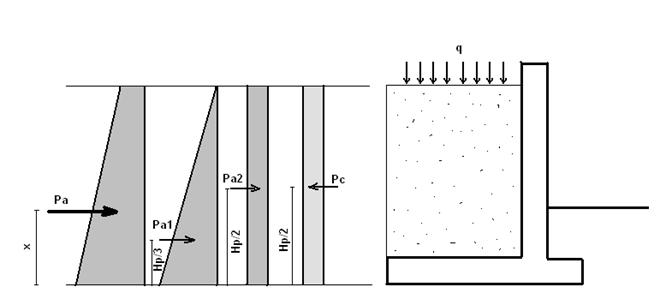
II. Note de calcul referitoare la dimensionarea si verificarea zidului de sprijin.

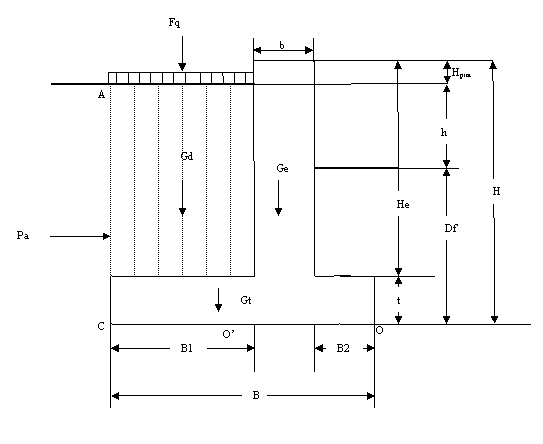
Fig. 2. Dimensiunile unui zid de sprijin

Zidurile de sprijin de greutate sunt constructii masive, care rezista prin propria lor greutate la impingerea activa a pamantului. Aceasta se poate calcula cu ajutorul teoriei lui Coulomb, prin metoda Rankine sau grafo-analitic prin metoda Culmann.

2.1 Primul pas consta in dimensionarea zidului de sprijin. Punctul de plecare este dat de inaltimea H a zidului, celelalte dimensiuni fiind derivate ale acesteia. Astfel:

b se ia = H/12, dar ≥    0,3 m;

t = H/8 ÷ H/6 (in cazul nostru t = b = H/12);

H_e = H - t;

B₂ = t;

B se ia

B₁ = B - b - B₂

Dupa ce s-a realizat dimensionarea zidului se calculeaza solicitarile asupra zidului de sprijin (pentru 1 ml de zid). Se determina astfel fortele active (impingerea pamantului, impingerea sau subpresiunea apei), fortele pasive (reactiunile provenite din greutatea proprie a zidului), momentele generate de aceste forte fata de anumite puncte de pe talpa.