TEORIA ASUPRA SECRETIZARII SISTEMELOR

PARTEA I

STRUCTURA MATEMATICA A SISTEMELOR SECRETIZATE

2. SISTEME SECRETIZATE

Ca un prim pas in analiza matematica a criptografiei, este necesar sa idealizam situatia in mod corespunzator si sa definim intr-o modalitate, acceptabila matematic, ceea ce vrem sa intelegem prin sistem secretizat. O diagrama schematica a unui sistem general de secretizare este aratata in Fig. 1. La capatul transmitator exista doua surse de informatie - o sursa mesaj si o sursa cheie. Sursa cheie produce o cheie particulara din cele care sunt posibile in sistem. Aceasta cheie este transmisa prin diferite mijloace, de presupus neinterceptibile, de ex. printr-un mesager, la capatul receptor, la destinatie ("receiving end"). Sursa mesaj produce un mesaj (clarul) care este cifrat, iar criptograma rezultata este transmisa la destinatie prin mijloace, posibil interceptibile, de ex. prin radio. La destinatie, criptograma si cheile sunt combinate in decriptor, pentru a recupera mesajul.

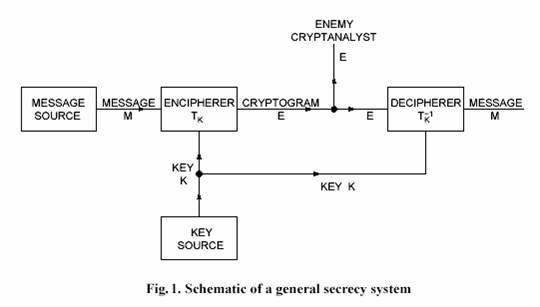
Evident, cifrarea realizeaza o operatie functionala. Daca M este mesajul, K este cheia si E mesajul cifrat, sau criptograma vom avea:

unde E este o functie de M si K. Este de preferat sa nu ne gindim la ea ca la o functie de doua variabile, ci ca o familie (cu un singur parametru) de operatii si de transformari si sa scriem:

Transformarea Ti aplicata mesajului M produce criptograma E. Indexul i corespunde cheii particulare care este folosita.

Vom presupune, in general, ca exista doar un numar finit de chei posibile, iar fiecare dintre ele are asociata probabilitatea p i. Astfel, sursa cheie este reprezentata de un proces sau un device statistic care alege una singura dintr-un set de transformari

respectiv cu probabilitatile

In mod similar, vom presupune un numar finit de mesaje posibile

cu probabilitatile asociate a priori

Mesajele posibile, de ex., pot fi secvente posibile de litere in engleza toate de lungime N, iar probabilitatile asociate sunt atunci frecventele relative de aparitie a acestor secvente in textul Englez normal.   

La capatul receptor (destinatie) este posibil sa regasesti pe M, cunoscand pe E si pe K.

Atunci transformarile din familie trebuie sa aiba inversre unice ,

astfel incat

,

unde I este transformarea unitate. Atunci :

De fiecare data, aceasta inversa trebuie sa fie unica pentru fiecare E care poate fi obtinut din M cu cheia i. De aici ajungem la definitia urmatoare:

Un sistem secretizat reprezinta o familie de transformari reversibile unice ale unui set de mesaje posibile intr-un set de criptograme, transformarea avand asociata probabilitatea .

Conversia oricarui set de entitati de acest tip va fi cunoscuta sub numele de sistem secretizat. Setul de mesaje posibile va fi numit, "spatiul de mesaje", iar setul de criptograme posibile va fi numit "spatiul criuptogramelor".

Doua sisteme secretizate pot fi vizualizate mecanic drept o masina cu unul sau mai multe controale pe ea. O secventa de litere, mesajul, se afla la intrarea in masina si serii secunde sunt la iesire.

Sunt facute setari particulare ale controalelor corespunzatoare cheilor particulare utilizate. Trebuie aplicate unele metode statistice pentru a alege cheia din cele posibile.

Pentru a face problema abordabila din punct de vedere matematic, va trebui sa presupunem ca inamicul cunoaste sistemul care va fi folosit.

Astfel, el cunoaste familia de transformari si probabilitatile de alegere a diferitelor chei. Se poate obiecta ca aceasta presupunere este nerealista, deoarece, de cele mai multe ori, criptanalistul nu cunoaste ce sistem este folosit sau probabilitatile respective. Exista doua raspunsuri la aceste obiectii:

1. Restrictia este mult mai slaba decat apare la inceput, datorita definitiilor noastre referitoare la ceea ce inseamna un sistem secretizat. Presupunem ca un cripanalist intercepteaza mesajul si nu stie despre transpozitia de substitutie sau daca a fost folosit cifrul de tip Vigenère. El poate considera ca mesajul a fost cifrat printr-un sistem in care o parte din cheie face referire la care dintre aceste tipuri a fost utilizat, iar urmatoarea parte reprezentand cheia particulara pentru tipul respectiv. Aceste trei posibilitati diferite au asignate probabilitati in functie de cele mai bune estimari ale probabillitatilor a priori ale cifratorului, folosind tipurile corespunzatoare de cifru.

2. Presupunerea este cea folosita in mod curent in studiile criptografice. Este pesimista si oarecum nesigura, dar realista, din moment ce cineva ar trebui sa se astepte ca sistemul sau sa fie, eventual,deja finalizat. Astfel, chiar atunci cind un intreg nou sistem este divizat, astfel incat inamicul sa nu ii poata asigna orice probabilitate a priori fara a se dezvalui pe sine, cineva trebuie sa traiasca cu iluzia eventualei sale cunoasteri.

Situatia este similara cu cea intalnita in teoria jocurilor, unde se presupune ca inamicul gaseste strategia de joc utilizata. In ambele cazuri, presupunerea serveste pentru a descrie cunostintele inamicului.

O obiectie secunda posibila la definitia noastra pentru sistemele secretizate este aceea ca nu se tine cont de practica des intalnita de inserare de zerouri in mesaj si de utilizarea de substitutii multiple. In astfel de cazuri, nu exista o criptograma unica pentru un mesaj dat si o cheie data, dar cifratorul poate alege dintr-un numar de criptograme diferite. Se poate face aceastei situatii, doar daca se adauga complexitate stadiului prezent, fara sa altereze nici unul din rezultatele de baza.

Daca mesajele sunt produse printr-un proces Markov de tipul celui descris in (1) care sa reprezinte sursa de informatie, probabilitatile de mesaje diferite sunt determinate de structura procesului Markov. In momentul de fata, oricum, dorim sa avem o vedere de ansamblu, generala, a situatiei si sa privim mesajele mai degraba ca pe un set de entitati cu probabilitatile lor asociate, nu neaparat compuse ca o secventa de litere si nu in mod necesar produse printr-un proces Markov.

Trebuie subliniat faptul ca un sistem secretizat inseamna nu una, ci un set de mai multe transformari. Dupa ce cheia este aleasa, doar una dintre aceste transformari este folosita si doar una poate conduce la definirea unui sistem secretizat drept o singura transformare intr-un limbaj. Inamicul, oricum nu cunoaste care cheie a fost aleasa si cheile posibile sunt la fel de importante pentru el ca si cea actuala. Intr-adevar, doar existenta acestor altor posibilitati ofera o oarecare secretizare sistemului. Din moment ce secretizarea este interesul major al nostru, vom fi fortati sa elaboram un concept pentru sistemul securizat definit mai sus. Acest tip de situatie, unde posibilitatile sunt la fel de importante ca si cele actuale, reale, apare frecvent in jocurile de strategie. Desfasurarea unui joc de sah este in cea mai mare parte controlata de amenintari care nu se iau in considerare. Intr-un fel este similar cu "existenta virtuala" a imputarilor nerealizate in teoria jocurilor.   

Poate fi notat ca o singura operatie intr-un limbaj formeaza un tip degenerat de sistem secretizat, din punct de vedere al definitiei noastre - un sistem cu o singura cheie de probabilitate unitara (probabilitatea = 1).

Un astfel de sistem nu prezinta nici o secretizare - criptanalistul gaseste mesajul prin aplicarea inversei acestei transformari, singura de altfel din sistem, criptogramei interceptate. Cifratorul si criptanalistul poseda, in acest caz, aceeasi informatie. In general, singura diferenta intre cunostintele cifratorului si cele ale inamicului (criptanalistului) este aceea ca respectivul cifrator cunoaste cheia particulara ce este folosita, in timp ce criptanalistul stie doar probabilitatile a priori ale diferitelor chei din set.

Procesul de descifrare (decriptare) este acela prin care se aplica inversa unei transformari particulare care a fost folosita la obtinerea criptogramei.

Procesul de criptanaliza reprezinta o incercare de a determina mesajul (sau cheia particulara), fiind data doar criptograma si probabilitatile a priori ale diferitelor chei si mesaje.

Exista un numar de intrebari epistemologice dificile legate de teoria secretizarii, sau de orice teorie care implica aspecte ale probabilitatii (in particular probabilitati a priori, teorema Bayes, etc.) care sunt aplicate unei situatii practice. Tratate in mod abstract, teoria probabilitatii poate pune baza unei logici riguroase cu ajutorul abordarii teoriei moderne a masuratoarilor.

Aplicate unor situatii practice (physical), in special cand se au in vedere probabilitati subiective ("subjective") si experimente nerepetabile, apar multe intrebari ale validitatii logice. De ex., in abordarea secretizarii facuta aici, se presupune ca probabilitatile a priori ale diferitelor chei si mesaje sunt cunoscute de criptograful inamic - cum poate determina operational cineva daca estimarile sale sunt corecte, pe baza cunoastintelor lui asupra situatiei?

Pot fi construite situatii criptografice artificiale de tipul "urna si zar" (eng.: urn and die) in care probabilitatile a priori au inteles clar definit si idealizarea utilizata aici este sigur corespunzatoare. In alte situatii, pe care ni le putem imagina, de ex., o comunicatie interceptata intre invadatorii martieni, probabilitatile a priori vor fi atat de nesigure ca si cum ar fi lipsite de semnificatie. Cele mai multe situatii criptografice practice se afla intre aceste limite. Un criptanlist poate face o clasificare a mesajelor posibile in urmatoarele categorii: "rezonabile", "posibile dar improbabile" si "nerezonabile", alte subdiviziuni fiind fara sens.

Din fericire, in situatiile practice, doar erori extreme in probabilitatile a priori ale cheilor si mesajelor produc erori semnificative in parametri importanti. Aceasta, din cauza comporatmentului exponential al numarului de mesaje si criptograme si a masurilor logaritmice luate.

Reprezentarea sistemelor

Un sistem secretizat cum am descris mai sus poate fi reprezentat in mai multe feluri. Una dintre ele este convenabila, din motive ilustrative, este diagrama de linii, ca in Fig. 2.

Mesajele posibile sunt reprezentate prin puncte la stanga, iar criptogramele posibile prin puncte la dreapta. Daca o cheie sigura, sa presupunem cheia 1, transforma mesajul M₂ intr-o criptograma E₄ , atunci M₂ si E₄ sunt legate printr-o linie numita 1, etc.

Din fiecare mesaj posibil trebuie sa porneasca o linie pentru fiecare cheie diferita. Daca aceeasi este adevarata pentru fiecare criptograma, vom spune ca sistemul este inchis.

O metoda des intalnita pentru descrierea unui sistem este prin stabilirea unei operatii (unu) care sa actioneze asupra mesajului, pentru o cheie arbitrara, pentru a obtine criptograma. Similar, unu defineste implicit probabilitatile pentru diferite chei prin descrierea felului in care cheia este aleasa sau prin ceea ce stim despre obiceiurile inamicului de a-si alege cheile. Probabilitatile pentru mesaje sunt implicit determinate prin stabilirea cunostintelor a priori despre obiceiurile de limbaj ale inamicului, situatia tactica (care va influenta probabil continutul mesajului) si orice informatie speciala pe care o putem avea in legatura cu criptograma.

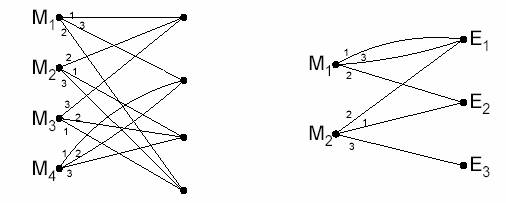
SISTEM INCHIS SISTEM DESCHIS

Fig.2. Desenarea de linii pentru sistemele simple

4. Unele exemple de sisteme secretizate

In aceasta sectiune vor fi date cateva exemple de cifruri. Acestea vor fi referite cel mai adesea in restul lucrarii (documentului) in scopuri ilustrative.

1. Cifrul de substitutie simpla (Simple Substitution Cipher).

In aceasta cifrare, fiecare litera a mesajului este inlocuita printr-un substitut simplu, de obicei tot cu o litera. Astfel, mesajul,

unde

reprezinta literele succesive care devin:

unde functia f(m) este o functie cu o inversa. Cheia este o permutare a alfabetului (cand substituentii sunt litere din alfabet), ex.

Prima litera X este substitutul lui A, G este substitutul lui B, etc.

2. Transpozitia (Perioada fixa d).

Mesajul este divizat in grupuri de lungime d, iar permutarea aplicata primului grup este aceeasi care este aplicata si grupului secund, etc. Permutarea este cheia si poate fi reprezentata printr-o permutare a primilor d intregi. Astfel, pentru d=5, putem avea 2 3 1 5 4 ca permutare. Aceasta inseamna ca:

devine:

Aplicarea in ordine (succesiva) a doua sau mai multe transpozitii va fi denumita transpozitie compusa (multipla). Daca perioadele sunt

este clar ca rezultatul este transpozitia de perioada d, unde d este cel mai mic multiplu comun al

3. Vigenère si variatiile

In cifrul Vigenère cheia reprezinta o serie de d litere. Acestea sunt scrise in mod repetat sub mesaj si doua adaugate modulo 26 (considerand alfabetul numerotat de la A=0 la Z=25). Astfel,

Unde k i se refera la perioada d cu indexul i. De ex., cu cheia :

Vom obtine:

Mesaj N O W I S T H E

Cheia repetitiva G A H G A H G A

Criptograma T O D O S A N E

Vigenère de perioada 1 este numit cifrul Cezar. Este o simpla substitutie in care fiecare litera din M este avnasata cu o cantitate fixa in alfabet. Aceasta cantitate este cheia, care poate fi orice valoare intre 0 si 25. Asa numitul Beaufort si Variant Beaufort sunt similare cu Vigenère si cifrat prin ecuatiile:

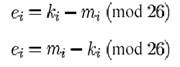
Beaufort de perioada unu este numit cifrul Cezar reversibil.

Aplicarea a doua sau mai multe Vigenère succesiv vor fi numite Vigenère compus. Va avea ecuatia:

unde

au in general diferite perioade. Perioada sumei lor:

in transpozitia compusa, este cel mai mic multiplu comun al perioadelor individuale.

Cand Vigenère este utilizat cu o cheie nelimitata, care nu se repeta niciodata, avem sistemul Vernam (NOTA: G. S. Vernam, "Cipher Printing Telegraph Systems for Secret Wire and Radio Telegraphic Communications," Journal American Institute of Electrical Engineers, v. XLV, pp. 109-115, 1926), cu:

unde

a fost aleasa la intamplare si independent intre 0,1,, 25.

Daca respectiva cheie este un text cu semnificatie(inteles) vom avea un cifru cu cheie variabila (eng.:"running key")

4. Substitutii diagrame, trigrame si n-grame

Mai repede ca substitutia pentru litere putem avea substitutia pentru digrame, trigrame, etc. Substitutiile cu digrame generale necesita o cheie formata dintr-o permutare de

digrame. Ea poate fi reprezentata printr-un tabel in care liniile corespund primei litere a digramei, iar coloana, celei de-a doua litere, intrarile in tabel fiind substitutiile (de obicei, deasemenea digrame).

5. Alfabet mixt singular Vigenère

Este o substitutie simpla urmata de Vigenère.

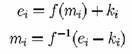
"Inversa" acestui sistem este Vigenère urmata de o substitutie simpla

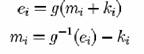
6. Sistem matrice

O metoda de substitutie cu n grame este aceea de a opera pe n grame succesive cu o matrice care are inversa (NOTA: Vezi L. S. Hill, "Cryptography in an Algebraic Alphabet," American Math. Monthly, v. 36, No. 6, 1, 1929, pp. 306-312; also "Concerning Certain Linear Transformation Apparatus of Cryptography," v. 38, No. 3, 1931, pp. 135-154 Literelor le sunt asociate cifre si numere intre 0 si 25, realizandu-se un inel algebric. Din grama n

ale mesajului, matricea

va da grama n a criptogramei

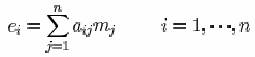
Matricea

Este cheia, iar descifrarea se face cu ajutorul matricei inverse. Matricea inversa va exista doar daca determinantul

Are un element invers in inel.

7. Cifrul "Playfair"

Este un tip particular de substitutie cu digrama bazata pe un alfabet de litere mixate in numar de 25, scris intr-un patrat de 5*5. (Litera J este data la o parte in munca criptografica - este foarte putin frecvent si cand apare poate fi inlocuit cu I). Presupunem ca patratul corespunzator cheii este asa cum este preyentat mai jos:

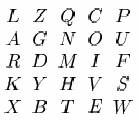
Substitutul pentru diagrama AC, de exemplu, este o pereche de litere din celelalte colturi ale patratului definit prin A si C, de ex. LO, L fiind luat primul, din moment ce este deasupra lui A. Daca digrama formata din litere este pe linia orizontala ca RI, se vor folosi literele din dreapta lor DF; RF devine DR. Daca literele sunt pe linia verticala, sunt folosite literele de mai jos. Astfel, PS devine UW. Daca literele sunt aceleasi, pot fi folosite zerouri pentru a le separa sau pot fi omise, etc.

8. Multiple Mixed Alphabet Substitution.

In acest cifru exista un set de l substitutii simple care sunt utilizate in secventa. Daca perioada d este

Devine

9. Cifru autochei.

Un sistem de tip Vigenère in care fiecare mesaj (sau criptograma rezultata) este folosita pentru "cheie" este denumit cifru cu autocheie. Cifrarea porneste cu o "cheie primara" (care este cheia intreaga in sensul nostru???) si continua cu mesajul sau criptograma inlocuite de lungimea cheii primare, asa cum am aratat mai sus, unde cheia primara este COMET. Mesajul utilizat drept "cheie":

Mesajul S E N D S U P P L I E S

Cheia C O M E T S E N D S U P

Criptograma U S Z H L M T C O A Y H

10. Cifruri fractionale

In acestea, fiecare litera este pentru inceput cifrata in doua sau mai multe litere sau numere si aceste simboluri sunt amestecate intr-un fel (de ex., prin transpozitie). Rezultatul poate apoi sa fie retranslatat in alfabetul original. Astfel, folosind un alfabet de litere mixat pentru cheie, literele pot fi translatate in numere in baza 5 ??? prin tabela:

Astfel B devine 41. Dupa ce seria rezultata de numere este transpusa intr-un anumit fel, numerele sunt luate perechi si translatate din nou in litere.

11. Coduri

In cuvintele coduri (sau uneori silabe), ele sunt inlocuite (substituite) cu grupuri de litere. Uneori, un cifru de un anumit tip sau altul este aplicat rezultatului.

5. Evaluarile sistemelor secretizate

Exista un numar de criterii diferite care ar trebui sa fie aplicate in cazul estimarii valorii sistemului secretizat propus. Cele mai importante dintre acestea sunt:

1. Cantitatea secretizarii.

Exista unele sisteme care sunt perfecte - inamicul nu este mai bun (dupa ce intercepteaza orice cantitate de material) decat inainte. Alte sisteme, desi furnizeaza inamicului unele informatii, nu dau o "solutie" pentru criptogramele interceptate. Printre sistemele solutionabile in mod unic, exista o paleta larga de variante pentru efortul cerut, necesar de a se obtine o astfel de solutie si pentru ca materialul interceptat sa furnizeze solutia unica.

2. Dimensiunea cheii.

Cheia trebuie transmisa (de la transmitator la receptor) prin mijloace neinterceptibile. Uneori, ea trebuie chiar memorata. Este de dorit sa avem o cheie cat mai mica.

3. Complexitatea operatiilor de cifrare si descifrare.

Cifrarea si descifrarea trebuie sa fie, desigur, cat mai simple. Daca aceste operatii sunt facute manual, se poate pierde mult timp, pot apare erori. Daca sunt facute mecanic, complexitatea este lasata masinilor.

4. Propagarea erorilor.

In tipurile de cifrari sigure, o eroare de o litera in procesul de cifrare sau transmisie conduce la un numar mare de erori in textul descifrat. Erorile apar in procesul de descifrare, cauzand pierderea de informatii si de cele mai multe ori este necesara retransmiterea criptogramei. Este, in mod normal, de dorit ca aceste erori sa fie minimizate.

5. Expansiunea (cresterea) mesajului.

In unele tipuri de sisteme secretizate, dimensiunea mesajului creste prin procesul de cifrare. Acest efect care nu este de dorit poate fi intalnit in sistemele in care se incearca incarcarea mesajului prin adaugarea de zerouri sau in sistemele in care sunt folosite substitutii multiple. De asemenea, acest efect poate apare si in multe tipuri de sisteme "acoperite, deghizate"(care nu sunt considerate sisteme secretizate in sensul definitiei noastre).

6. Algebra sistemelor secretizate

Daca avem doua sisteme secretizate T si R, le putem combina in diferite feluri pentru a alcatui un nou sistem secretizat S. Daca T si R au acelasi domeniu (spatiu al mesajului) vom putea forma un fel de "suma ponderata",

S=pT+qR

unde p+q=1. Aceasta operatie consta in prima faza in a face o alegere preliminara cu probabilitatile p si q pentru a determina care dintre T sau R este utilizat. Aceasta alegere este parte a cheii lui S. Dupa ce aceasta este determinata, T sau R este folosit asa cum este definit original. Cheia totala a lui S trebuie sa specifice care dintre T si R este folosit si care cheie a lui T sau R este folosita.

Daca T este format din transformarile T₁,,T_m cu probabilitatile p₁, , p_m si R este format din transformarile R₁,,R_k cu probabilitatile q₁,,q_k, atunci S = pT+qR este format din transformarile T₁,,T_m, R₁,,R_k cu probabilitatile pp₁, , pp_m, si respectiv qq₁,,qq_k.

Mai general putem forma suma unui numar de sisteme.

De notat ca orice sistem T poate fi scris ca o suma de operatii fixe:

T_i fiind operatia de cifrare explicita a lui T ce corespunde cheii alese i, care are probabilitatea p_i.

O alta cale de a combina doua sisteme secrete este prin a lua "produsul", prezentat sistematic in Fig.3.

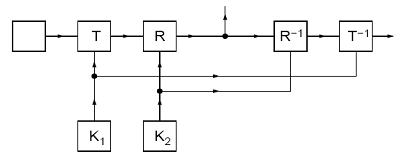
Figura 3. Produsul a doua sisteme S=RT

Presupunem ca T si R sunt doua sisteme si domeniul (spatiul de cuvinte) al lui R poate fi identificat cu domeniul (spatiul criptogramei) al lui T. Apoi, putem aplica la inceput pe T limbajului nostru si apoi R la rezultatul acestui proces de cifrare. Aceasta da operatia rezultanta S pe care il vom scrie ca un produs:

Cheia pentru S consta in ambele chei T si R care se presupune ca sunt alese in acord cu probabilitatile lor si independente. Astfel, daca o cheie m a lui T este aleasa cu probabilitatile

si cheia n a lui R are probabilitatile

Atunci S are cel mult mn chei cu probabilitatile

In multe cazuri, cateva dintre transformarile produsului

vor fi aceleasi si pot fi grupate impreuna, adaugand probabilitatile lor.

Cifrarea produsului este deseori utilizata. De exemplu, cand o substitutie este urmata de o transpozitie sau o transpozitie de o Vigenère, sau cand este aplicat un cod textului si este cifrat rezultatul printr-o substitutie, transpozitie, fractionare, etc.

De notat ca, in general, multiplicarea nu este comutativa (nu putem avea intotdeauna RS=SR), desi, in cazuri speciale, cum ar fi substitutia si transpozitia, este. Asta, atat timp cat reprezinta o operatie care este definita ca fiind asociativa. Astfel,

Mai mult, avem legile:

(legea asociativitatii pentru adunare)

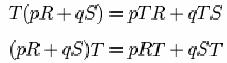
(legile distributivitatii la stanga si la dreapta)

si

Trebuie mentionat ca aceste operatii combinate, de adunare si multiplicare, sunt aplicate sistemelor secretizate ca un intreg. Produsul a doua sisteme TR nu trebuie confundat cu produsul transformarilor in sistemele:

care apare deasemenea in aceasta lucrare.

Produsul TR este un sistem secretizat, adica un set de transformari cu probabilitatile asociate; ultimul este o transformare particulara. Mai departe, suma a doua sisteme pR qT este un sistem - suma a doua transformari nu este definita. Sistemele T si R pot comuta fara ca T_i si R_i sa comute, astfel incat daca R este un sistem Beaufort de perioada data, toate cheile sunt la fel.

In general, dar desigur RR nu depinde de ordinea sa; intr-adevar,

Vigenère de aceeasi perioada cu cheia aleatoare. Pe de alta parte, daca T_i si R_i a doua sisteme T si R comuta, atunci sistemele comuta.

Un sistem pentru care spatiile M si E pot fi identificate, un caz comun este acela in care secventele de litere sunt transformate in secventele de litere, numit endomorfism ("endomorphic"). Un sistem endomorfic poate fi adus la puterea Tⁿ.

Un sistem secretizat T al carui produs cu el insusi este egal cu T, adica:

Va fi numit idempotent. De exemplu, substitutia simpla, transpozitia de perioada p, Vigenère de perioada p (toate cu chei asemanatoare) sunt idempotente.

Setul tuturor sistemelor secretizate endomorfice definite intr-un spatiu al mesajului fixat constituie o "varietate algebrica", ceea ce este un fel de algebra, care foloseste operatii de insumare si inmultire. De fapt, proprietatea de adunare si inmultire despre care am discutat pot fi prezentate dupa cum urmeaza:

Un set de cifruri (cifrari) cu acelasi spatiu al mesajului si cele doua operatii de combinare, de adunare ponderata si inmultire, formeaza o algebra asociativa lineara cu un element unitate, in plus, coeficientii dintr-o suma ponderata trebuie sa fie pozitivi iar suma lor sa fie egala cu unu.

Operatiile combiante ne dau modalitati de a construi multe tipuri noi de sisteme secretizate, sigure, cum sunt cele date in exemple. Le vom folosi deasemenea pentru a descrie situatia cu care se confrunta un criptanalist cand incearca sa rezolve o criptograma de un tip necunoscut. El rezolva, de fapt, un sistem secretizat de tipul:

unde A, B, ,S sunt tipuri cunoscute de cifruri, cu p_i probabilitatile a priori, in aceasta situatie si

corespunde posibilitatii unui complet nou si necunoscut tip de cifru.

7. Cifruri pure si mixate

Tipurile sigure de cifruri cum ar fi substitutiile simple, transpozitiile de perioada data, Vigenère de perioada data, alfabetul mixat Vigenère, etc. (toate cu chei asemanatoare) prezinta o omogenitate sigura in acord cu cheia. Indiferent de cheie, cifrarea, descifrarea si procesul de decriptare sunt in esenta la fel. Aceasta poate contrasta cu cifrul:

unde S este o substitutie simpla, iar T o transpozitie de perioada data. In acest caz, intregul sistem se schimba pentru cifrare, descifrare si decriptare si depinde de folosirea fie a transpozitiei, fie a substitutiei.

Cauza omogenitatii ("homogeneity") in aceste sisteme este stopata ("stems") de proprietatea grupului - de mentionat ca, in exemplele de mai sus de cifruri omogene, produsul T_iT_j al oricaror doua transformari din set este egal cu o a treia transformare T_k din set. Pe de alta parte TiSj nu este egal cu orice transformare din cifrul

care contine doar substitutii si transpozitii, nu produse.

Putem defini un cifru "pur" atunci cand T_i formeaza un grup. Acesta poate fi prea restrictiv din moment ce necesita ca spatiul E sa fie la fel cu spatiul M, astfel incat sistemul sa fie endomorfic. Transpozitia este la fel de omogena ca o transpozitie obisnuita fara a fi endomorfica. Definitia corespunzatoare este precum urmeaza: Un cifru T este pur daca pentru fiecare T_i ,T_j ,T _k exista un T_s astfel incat:

si fiecare cheie este asemanatoare ("equally likely"). Altfel, cifrul este mixat. Sistemele din Fig. 2 sunt mixate. In Fig. 4 este un sistem pur, daca toate cheile sunt asemanatoare.

Teorema1.

Intr-un cifru (cifrare) pur operatiile:

care transforma spatiul mesajului in el insusi, formeaza un grup de ordin m, adica numarul de chei diferite.

Pentru

Fiecare element are o inversa. Legea asociativa este adevarata, atat timp cat acestea sunt operatiiile, iar proprietatea de grup reiese din:

folosind presupunerea ca:

pentru un s.

Operatia

inseamna, desigur, cifrarea mesajului cu cheia j si apoi descifrarea cu cheia i, care ne conduce inapoi la spatiul mesajului. Daca T este endomorfica, astfel incat T i transforma spatiul

in el insusi (asa cum este in cazul multor cifruri, in care, atat spatiul mesajului, cat si spatiul criptogramei reprezinta secvente de litere, cuvinte), iar transformarile T_i reprezinta un grup si sunt asemanatoare "equally likely", atunci T este pur, cat timp:

Teorema 2. Produsul a doua cifruri pure, care comuta, este tot un cifru pur.

Daca T si R comuta

pentru fiecare i, j cu l, m, corespunzatoare avem si:

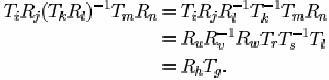
Conditia de comutare nu este necesara pentru ca produsul sa fie un cifru pur.

Un sistem cu o singura cheie, cu o singura operatie definita T₁ este pur, deoarece avem:

Astfel, expansiunea unui cifru general intr-o suma de transformari simple este reprezentat ca o suma de cifruri pure.

O examinare a unui exemplu de cifru pur aratat in Figura 4. dezvaluie proprietatile sigure. Mesajele sunt introduse in subseturi pe care le vom numi clase reziduale, iar posibilele criptograme sunt impartite in clasele reziduale corespunzatoare. Exista cel putin o linie de la fiecare mesaj dintr-o clasa la fiecare criptograma in clasa corespunzatoare si nici o linie intre clasele care nu corespund. Numarul de mesaje dintr-o clasa este un divizor al numarului total de chei. Numarul de linii "in paralel" de la un mesaj M la o criptograma, in clasa corespunzatoare, este egal cu numarul cheilor impartit (separat) la (de) numarul mesajelor din clasa ce contine mesajul (sau criptograma). Este aratat in anexa ca aceasta se intampla in general pentru cifrurile pure. Sintetizand, obtinem:

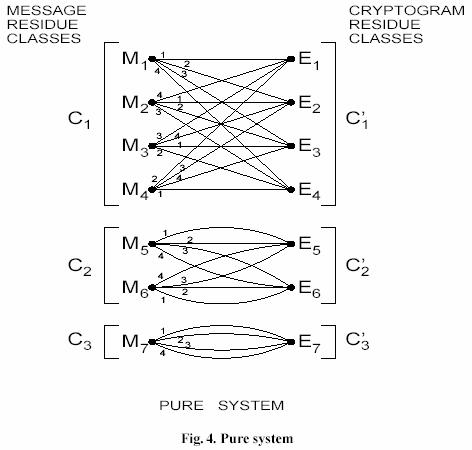
Teorema 3. Intr-un sistem pur mesajele pot fi impartite intr-un set de "clase reziduale":

Iar criptogramele intr-un set de "clase reziduale" :

cu urmatoarele proprietati:

(1) Clasele reziduale ale mesajelor sunt exclusive mutual si impreuna contin toate mesajele posibile. Similar pentru clasele reziduale ale criptogramelor.

(2) Cifrarea oricarui mesaj in C_i cu orice cheie produce o criptograma in C_i. Descifrarea oricarei criptograme in C_i cu orice cheie conduce la un mesaj in C_i .

(3) Numarul de mesaje in C_i , fie

este egal cu numarul de criptograme din

si este un divizor al lui k, numarul de chei.

(4) Fiecare mesaj din C_i poate fi cifrat in fiecare criptograma din

prin exact

chei diferite. Similar, pentru descifrare.

Importanta conceptului unui cifru pur (si motivul pentru nume) reiese din faptul ca intr-un cifru pur toate cheile sunt, in esenta, la fel. Indiferent ce cheie este folosita pentru un anumit mesaj, probabilitatile a priori ale tuturor mesajelor sunt identice. Pentru a vedea aceasta, se considera doua chei diferite care, aplicate aceluiasi mesaj, conduc la doua criptograme care fac parte din aceeasi clasa a rezidurilor, sa presupunem:

.

Cele doua criptograme pot fi apoi descifrate prin

chei in fiecare mesaj din C_i si nu in alte mesaje posibile.

Toate cheile care sunt la fel, asemanatoare cu probabilitatile a posteriori ale diferitelor mesaje sunt atunci:

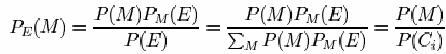
unde M este in C_i , E este

iar suma este peste toate mesajele din C_i. Daca E si M nu sunt clase reziduale corespunzatoare, P_E(M) = 0. In mod similar, poate fi aratat ca probabilitatile a posteriori ale diferitelor chei sunt aceleasi in valoare, dar aceste valori sunt asociate cu diferite chei, cand este utilizata. Acelasi set de valori ale lui P_E(K) prezinta cate o permutare prin chei. Astfel, obtinem rezultatul.

Teorema 4. Intr-un sistem pur probabilitatile a posteriori ale diferitelor mesaje P_E(M) sunt independente de cheia aleasa. Probabilitatile a posteriori ale cheilor P_E(K) sunt aceleasi in valoare, dar permutate prin alegerea unei chei diferite.

Se mai poate spune ca orice alegere a cheii conduce la aceeasi problema criptanalitica intr-un cifru pur. Deoarece chei diferite conduc la criptograme din aceeasi clasa reziduala, inseamna ca toate criptogramele, din aceeasi clasa reziduala, sunt criptanalitic echivalente - ele conduc la aceleasi probabilitati a posteriori ale mesajelor si diferite prin permutare, la aceleasi probabilitati ale cheilor.

Ca in exemplul acesta, o substitutie simpla cu toate cheile la fel, este un cifru pur. Clasa reziduala ce corespunde unei criptograme date E reprezinta setul tuturor criptogramelor care pot fi obtinute din E prin operatiile:

In acest caz,

este in sine o substitutie si, in consecinta, orice substitutie pe E va da un alt membru al aceleiasi clase reziduale. Astfel, daca respectiva criptograma este

atunci:

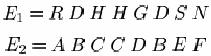
sunt in aceeasi clasa reziduala. Este evident in acest caz ca aceste criptograme sunt in esenta echivalente. Ceea ce este important intr-o substitutie simpla cu cheie aleatoare este paternul (modelul) repetitiilor literelor (cuvintelor, secventelor), literele actuale fiind slab variabile. Intr-adevar, ne putem dispensa de ele de tot, indicand peternul (modelul) repetitiilor din E, dupa cum urmeaza:

Aceasta notatie descrie clasa reziduala, dar elimina toate informatiile referitoare la um membru specific al clasei. Astfel, este pastrata acea informatie care este pertinenta din punct de vedere criptanalitic. Aceasta se refera la o metoda de atac a cifrurilor cu substitutie simpla - metoda cuvintelor patern (model).

In cifrul de tip Cezar doar primele mod 26 diferente din criptograma sunt semnificative. Doua criptograme cu acelasi

se afla in aceeasi clasa reziduala.

O modalitate de spargere a acestui tip de cifru este cea realizata prin scrierea in ordine inversa a celor 26 de membrii din clasa reziduala a mesajului si acoaterea celui care are sens.

Un cifru de tip Vigenère de perioada d cu cheia aleatoare este un alt exemplu de cifru pur. Aici, clasa reziduala a mesajului este alcatuita din toate secventele cu aceleasi prime diferente ca si criptograma, pentru literele separate prin distanta d. Pentru d=3 clasa de reziduuri este definita astfel:

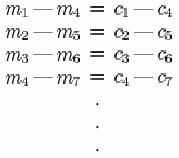
unde E = e₁, e₂, e₃, este criptograma, iar m₁,m₂, este orice M in clasa reziduala corespunzatoare.

In cifrul de traspozitie de perioada d cu cheie aleatoare, clasa reziduala este alcatuita din toate argumentele lui e_i in care nici un e_i nu este mutat in afara blocului lui de lungime d, si oricare doua e_i la distanta d, raman la aceasta distanta. Aceasta este folosita la spargerea acestor blocuri, dupa cum urmeaza: Criptograma este scrisa in blocuri succesive de lungime d, unul sub altul, dupa cum urmeaza (d=5):

Coloanele sunt apoi taiate, indepartate si rearanjate, pentru a alcatui un text cu inteles. Cand coloanele sunt indepartate, singura informatie care ramane este clasa reziduala a criptogramei.

Teorema 5. Daca T este pur atunci:

unde T_iT_j sunt oricare doua transformari ale lui T. Reciproc, daca aceasta relatie este adevarata, pentru oricare T_iT_j intr-un sistem T, atunci T este pur.

Prima parte a acestei teoreme este evidenta din definitia unui sistem pur. Pentru a demonstra cea de-a doua parte, vom nota mai intai ca, in cazul in care:

atunci,

este o transformare a lui T. Ramane de vazut ca toate cheile sunt echiprobabile. Vom avea:

si:

Termenul din partea stanga a sumei cu s=j devine:

Singurul termen in T i din partea dreapta este:

Din moment ce toti coeficientii sunt pozitivi (ne-negativi), rezulta:

Acelasi argument poate avea i sau j, care interschimba si in consecinta:

si T este pur. Astfel, conditia:

poate fi folosita ca o alternativa la definitia unui sistem pur.

8. Sisteme similare

Se spune despre doua sisteme R si S ca sunt similare, daca exista o transformare A care are o inversa A^-1, astfel incat:

Aceasta inseamna ca cifrarea cu R este aceeasi cu cifrarea cu S si apoi opeararea rezultatului cu transformarea A. Daca scriem:

inseamna ca R este similar cu S, fiind clar ca:

implica si:

Deasemenea:

si

implica:

si in final:

Se poate spune ca similaritatea este o relatie de echivalenta.

Insemnatatea similaritatii in criptografie este aceea ca daca:

Atunci R si S sunt echivalente din punct de vedere criptanalitic. Intr-adevar, daca un criptanalist intercepteaza o criptograma in sistemul S, el o poate transforma intr-una din sistemul R, doar aplicandu-i transformarea A. O criptograma in sistemul R este transformata intr-una din sistemul S aplicandu-i A^-1. Daca R si S sunt aplicate aceluiasi spatiu al mesajului sau aceluiasi limbaj, exista o corespondenta unu-la-unu intre criptogramele rezultate. Criptogramele corespunzatoare dau aceeasi corespondenta probabilitatilor a priori pentru toate mesajele.

Daca exista o metoda de a sparge sistemul R, atunci orice sistem S similar cu R poate fi spart (ajungand la R) prin aplicarea lui A. Aceasta este o modalitate frecvent utilizata in practica criptanalizei.

Ca un exemplu foarte simplu, trivial, substitutia simpla, in care substituentii nu sunt litere, ci simboluri aleatoare, este similara cu substitutia simpla in care se folosesc litere drept substituenti. Un al doilea exemplu este cifrul Cezar si cifrul Cezar reversibil. Cel de-al doilea este uneori spart de primul, fiind transformat intr-un cifru Cezar. Aceasta poate fi facuta prin inversarea alfabetului in criptograma. Cifrurile Vigenère, Beaufort si Beaufort Variant sunt toate similare, cand cheia este aleatoare. Cifrul cu "autocheie" (cu mesajul utilizat drept "cheie"), cu cheia:

este similara cu cifrul de tip Vigenère cu cheie alternativ adaugata si eliminata ????? Mod 26. Transformarea A in acest caz este de a "descifra" autocheia cu serii de cate d A-uri pentru cheia primara.

PARTEA A II-A

SECRETIZAREA TEORETICA

9. INTRODUCERE

Consideram acum problemele legate de "secretizarea teoretica" a unui sistem. Cat de imun este un sistem la o criptanaliza, atunci cand criptanalistul dispune de timp si de forta de lucru nelimitate pentru analiza criptogramelor? Are intr-adevar o criptograma o solutie unica (chiar daca ar fi nevoie de o cantitate nerezonabila de lucru pentru a o gasi), si daca nu, cate solutii rezonabile are ea? Cat de mult text dintr-un sistem dat trebuie interceptat inainte ca solutia sa devina unica? Exista sisteme care nu devin niciodata unice ca solutie, indiferent cat de mult text cifrat este interceptat? Exista sisteme pentru care nu este data nicio informatie, de orice fel, inamicului, indiferent cat de mult text este interceptat? In analiza acestor probleme, conceptele de entropie, redundanta si altele asemenea, dezvoltate in "O teorie matematica a comunicatiei" (engl.: A Mathematical Theory of Communication) (referita de aici incolo prin MTC) isi vor gasi o larga aplicare.

10. SECRETIZAREA PERFECTA

Sa presupunem ca mesajele posibile sunt finite in numar, M₁, , M_n si au probabilitati a priori P(M₁), , P(M_n) si ca acestea sunt cifrate in criptogramele posibile E₁, , E_m prin:

E T_iM.

Criptanalistul intercepteaza un E particular si poate apoi calcula, cel putin in principiu, probabilitatile a posteriori pentru diversele mesaje, P_E(M). Este natural sa definim secretizarea perfecta prin conditia in care, pentru toate E, probabilitatile a posteriori sunt egale cu probabilitatile a priori, independent de valorile acestora. In acest caz, interceptarea mesajului nu a oferit criptanalistului nicio informatie (NOTA: un puritan ar putea obiecta ca inamicul a obtinut o oarecare informatie, in ideea ca el stie ca a fost trimis un mesaj. Acestuia i se poate raspunde prin introducerea printre mesaje a unui "blanc", corespunzator cu "niciun mesaj". Daca nu este generat niciun mesaj, blancul este cifrat si trimis ca si criptograma. Atunci, chiar si aceasta mica parte de informatie ramasa este eliminata). Orice actiune a sa, care depinde de informatia continuta in criptograma nu poate fi modificata, deoarece toate probabilitatile sale referitor la ceea ce contine criptograma raman neschimbate. Pe de alta parte, daca nu este satisfacuta conditia, vor exista situatii in care inamicul are anumite probabilitati a priori, si pot aparea anumite alegeri ale cheii si mesajului pentru care probabilitatile inamicului intr-adevar se modifica. In schimb, acest lucru poate afecta actiunile sale si astfel secretizarea perfecta nu a fost obtinuta. De aceea, definitia data este ceruta in mod necesar de ideile noastre intuitive despre ceea ce ar trebui sa insemne secretizarea perfecta.

O conditie necesara si suficienta pentru secretizarea perfecta poate fi descoperita dupa cum urmeaza: avem teorema lui Bayes:

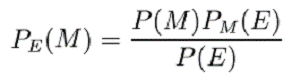
unde:

P(M) = probabilitatea a priori a mesajului M.

P_M(E) = probabilitatea conditionata a criptogramei E daca mesajul M este ales, adica suma probabilitatilor tuturor cheilor care produc criptograma E din mesajul M.

P(E) = probabilitatea de a obtine criptograma E din orice cauza.

P_E(M) = probabilitatea a posteriori a mesajului M daca criptograma E este interceptata.

Pentru secretizarea perfecta, P_E(M) trebuie sa fie egal cu P(M) pentru toate E si toate M. De aici, fie P(M)=0, o solutie care trebuie exclusa din moment ce avem nevoie de egalitate independent de valorile P(M), fie

P_M(E)=P(E)

pentru fiecare M si E. Pe de alta parte, daca P_M(E)=P(E), atunci

P_E(M)=P(M)

si avem secretizare perfecta. Astfel, avem rezultatul:

Teorema 6. O conditie necesara si suficienta pentru secretizarea perfecta este ca

P_M(E)=P(E)

pentru toate M si E. Aceasta inseamna ca P_M(E) trebuie sa fie independent de M.

Altfel spus, probabilitatea totala a tuturor cheilor care transforma M_i intr-o criptograma E data este egala cu cea a tuturor cheilor care transforma M_j in acelasi E, pentru toate M_i, M_j si E.

Acum, trebuie sa existe tot atatea E-uri cate M-uri, din moment ce, pentru un i fixat, T_i da o corespondenta unu‑la‑unu intre toate M-urile si o parte din E-uri. Pentru secretizare perfecta, P_M(E)=P(E) 0 pentru oricare din aceste E-uri si orice M. Astfel, exista cel putin o cheie care transforma orice M in oricare din aceste E-uri. Dar toate cheile de la un M fixat catre E-uri diferite trebuie sa fie diferite, si de aceea numarul cheilor diferite este cel putin la fel de mare ca numarul de M-uri.

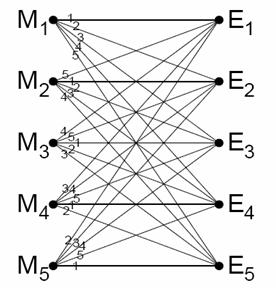
Fig. 5. Sistem perfect

Este posibil sa se obtina secretizarea perfecta doar cu acest numar de chei, asa cum se poate arata prin urmatorul exemplu: Fie M_i numerotat de la 1 la n si E_i la fel, si folosind n chei, fie

T_iM_j=E_s

Unde s=i+j(Mod n). In acest caz, observam ca P_E(M)=1/n=P(E) si avem secretizare perfecta. Este prezentat un exemplu in Fig. 5 cu s=i+j-1(Mod 5).

Sistemele perfecte in care numarul criptogramelor, numarul mesajelor si numarul cheilor sunt toate egale sunt caracterizate de proprietatea ca (1) fiecare M este legat de fiecare E prin exact o linie, (2) toate cheile sunt la fel de probabile (engl.: equally likely). Astfel, reprezentarea matriciala a sistemului este un "careu latin".

In MTC a fost aratat ca informatia poate fi masurata convenabil prin intermediul entropiei. Daca avem un set de posibilitati cu probabilitatile p₁, p₂, , p_n, entropia H este data de

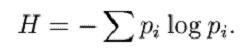
Intr-un sistem de secretizare sunt implicate doua optiuni statistice, cea a mesajului si cea a cheii. Putem masura cantitatea de informatie produsa atunci cand este ales un mesaj prin H(M):

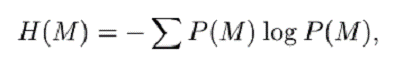
sumarea fiind peste toate mesajele posibile. Similar, exista o incertitudine asociata cu alegerea unei chei, data de:

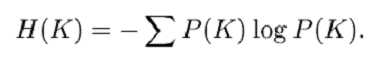
In sistemele perfecte de tipul descris mai sus, cantitatea de informatie din mesaj este cel mult log n (care are loc atunci cand toate mesajele sunt echiprobabile). Aceasta informatie poate fi complet mascata numai daca incertitudinea cheii este cel putin log n. Acesta este primul exemplu al unui principiu general care va aparea frecvent: acela ca exista o limita a ceea ce putem obtine cu o anumita incertitudine a cheii - cantitatea de incertitudine pe care o putem introduce in solutie nu poate fi mai mare decat incertitudinea cheii.

Situatia este oarecum mai complicata daca numarul mesajelor este infinit. Sa presupunem, de exemplu, ca ele sunt generate ca secvente infinite de litere printr-un proces Markov corespunzator. Este clar ca nicio cheie finita nu va da secretizare perfecta. Apoi, presupunem ca sursa de chei genereaza chei in acelasi mod, adica, ca o secventa infinita de simboluri. Sa presupunem mai departe ca doar o anumita portiune a cheii L_K este necesara pentru cifrarea si descifrarea unei portiuni L_M a mesajului. Fie logaritmul numarului de litere din alfabetul mesajului R_M si cel pentru alfabetul cheii R_K. Apoi, din cazul finit, este evident ca secretizarea perfecta necesita

R_M L_M R_K L_K.

Acest tip de secretizare perfecta este realizata de sistemul Vernam.

Aceste rezultate au fost deduse pe baza probabilitatilor necunoscute sau arbitrar a priori ale mesajelor. Cheia necesara pentru secretizarea perfecta depinde apoi de numarul total al mesajelor posibile.

Cineva s-ar astepta ca, daca spatiul mesajelor are statistici cunoscute fixate, astfel incat are o rata medie definita R de a genera informatiile, in sensul MTC, atunci cantitatea din cheie necesara ar putea fi redusa la media din chiar acest raport R/R_M, iar acest lucru este adevarat. De fapt, mesajul poate fi transferat printr-un transformator (engl.: transducer) care elimina redundanta si reduce lungimea, care este de asteptat sa apara, chiar la acest raport, iar apoi poate fi aplicat un sistem Vernam la rezultat. Evident ca, cantitatea din cheie utilizata pentru fiecare litera din mesaj este redusa statistic cu un factor R/R_M, si in acest caz sursa de chei si sursa de informatii chiar se potrivesc - un bit din cheie mascheaza complet un bit din informatia din mesaj. De asemenea, este lesne de aratat, prin metodele utilizate in MTC, ca aceasta este maximul care se poate obtine.

Sistemele de secretizare perfecte au un loc in imaginea practica - ele pot fi utilizate fie acolo unde cea mai mare importanta este acordata secretizarii complete - de exemplu corespondenta dintre cele mai inalte niveluri de comanda, fie in cazurile in care numarul mesajelor posibile este redus. Astfel, pentru a da un exemplu extrem, daca ar fi anticipate doar doua mesaje, "yes" sau "no" ("da" sau "nu"), un sistem perfect ar trebui sa fie functional, probabil cu tabela de transformare:

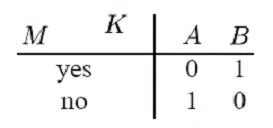
Dezavantajul sistemelor perfecte pentru sisteme mari de corespondente este, bineinteles, cantitatea echivalenta din cheie care trebuie trimisa. In sectiunile urmatoare vom lua in considerare ceea ce poate fi obtinut cu o dimensiune mai mica a cheii, in particular cu chei finite.

11. ECHIVOCITATE

Sa presupunem ca a fost folosit un cifru simplu de substitutie pe un text in engleza si ca interceptam o anumita cantitate, N litere, din textul cifrat. Pentru un N suficient de mare, sa spunem mai mare de 50 de litere, exista aproape intotdeauna o solutie unica pentru cifru; adica, o singura secventa buna in engleza care se transforma in materialul interceptat printr-o simpla substitutie. Cu un N mai mic, totusi, sansa mai multor solutii este mai mare: pentru N=15 va exista in general un numar considerabil de fragmente posibile din text care s-ar putea potrivi, in timp ce pentru N=8 este posibila o buna parte (de ordinul 1/8) din toate secventele rezonabile in engleza de acea dimensiune, din moment ce exista rar mai mult de o litera repetata in cele 8. Pentru N=1, orice litera este evident posibila, si are aceeasi probabilitate a posteriori ca si probabilitatea sa a priori. Pentru o litera, sistemul este perfect.

Acest lucru se intampla in general cu cifruri solvabile. Inainte de a intercepta orice material, ne putem imagina probabilitatile a priori atasate diverselor mesaje posibile, si de asemenea diverselor chei. O data ce materialul este interceptat, criptanalistul calculeaza probabilitatile a posteriori; iar pe masura ce creste N, cresc si probabilitatile anumitor mesaje, si, mai ales, descresc, pana cand ramane un singur mesaj, care are probabilitatea aproape de unu, in timp ce probabilitatile tuturor celorlalte este aproape de zero.

Aceste calcule pot fi efectuate in realitate pentru sisteme foarte simple. Tabela 1 prezinta probabilitatile a posteriori pentru un cifru de tip Cezar aplicat unui text in engleza, cu o cheie aleasa aleator din cele 26 de posibilitati. Pentru a permite folosirea tabelelor de frecventa ale unei litere standard, ale digramelor si trigramelor, textul a fost initializat intr-un punct aleator (prin deschiderea unei carti si plasarea unui creion la intamplare pe pagina). Mesajul selectat astfel incepe cu "creases to . " si incepe in interiorul cuvantului "increases". Daca s-ar fi stiut ca in mesaj incepe o propozitie noua, atunci trebuie folosit un set diferit de probabilitati, corespunzatoare frecventelor literelor, digramelor etc., de la inceputul propozitiilor.

Tabelul 1. Probabilitatile a posteriori pentru o criptograma de tip Cezar

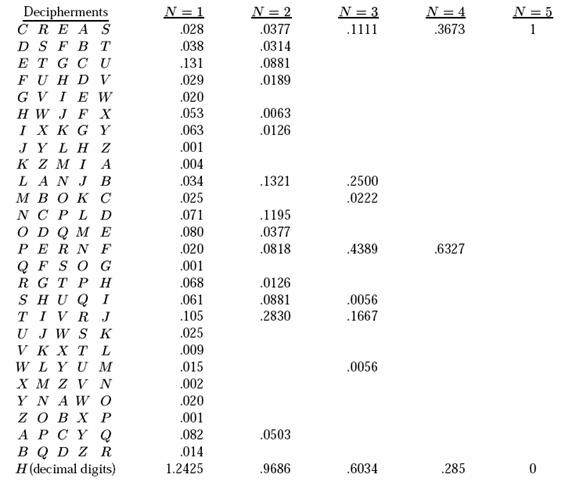
Cezar cu cheie aleatoare este un cifru pur, iar cheia particulara aleasa nu afecteaza probabilitatile a posteriori. Pentru a determina acestea, trebuie doar sa listam descifrarile posibile prin toate cheile si sa calculam probabilitatile lor a priori. Probabilitatile a posteriori sunt acestea impartite la suma lor. Aceste descifrari posibile sunt descoperite prin procesul standard de "parcurgere a alfabetului" (engl.: "running down the alphabet") din mesaj si sunt listate in partea stanga. Acestea formeaza clasa resturilor pentru mesaj. Pentru o litera interceptata, probabilitatile a posteriori sunt egale cu probabilitatile a priori pentru litere (NOTA: Probabilitatile pentru acest tabel au fost luate din tabelele de frecvente date de Fletcher Pratt in cartea "Secret si urgent", publicata de Blue Ribbon Books, New York, 1939. Desi incomplete, ele sunt suficiente pentru scopurile de fata) si sunt prezentate in coloana cu titlul N=1. Pentru doua litere interceptate, probabilitatile sunt cele pentru digrame, ajustate pentru ca suma lor sa dea unu (engl.: adjusted to sum to unity) si acestea sunt prezentate in coloana cu titlul N=2. Frecventele trigramelor au fost de asemenea introduse si sunt prezentate in coloana cu titlul N=3. Pentru secventele de 4 si 5 litere, probabilitatile au fost obtinute prin multiplicarea frecventelor trigramelor, deoarece, cu aproximatie,

p(ijkl)=p(ijk)p_jk(l).

Sa observam ca, la trei litere, campul a fost restrans la patru mesaje cu suficient de mare probabilitate, celelalte fiind relativ mici. La patru, exista doua posibilitati, iar la cinci doar una, descifrarea corecta.

In principiu, acest lucru poate fi realizat cu orice sistem, dar, in afara cazului in care cheia este foarte mica, numarul posibilitatilor este atat de mare incat lucrul implicat impiedica calculele efective.

Acest set de probabilitati a posteriori descrie modul in care cunostintele criptanalistului despre mesaj si cheie devin treptat mai precise pe masura ce este obtinut materialul cifrat. Aceasta descriere, totusi, este mult prea complicata si dificil de obtinut pentru scopurile noastre. Ceea ce dorim este o descriere simplificata a acestei abordari catre unicitatea solutiilor posibile.

O situatie similara provine in teoria comunicatiei atunci cand un semnal transmis este perturbat de zgomot. Este necesar sa se stabileasca o masura potrivita a incertitudinii asupra a ceea ce a fost transmis in realitate, cunoscand doar versiunea perturbata, data de semnalul receptionat. In MTC s-a aratat ca o masura matematica naturala a acestei incertitudini este entropia conditionata a semnalului transmis, atunci cand semnalul receptionat este cunoscut. Aceasta entropie conditionata a fost numita, pentru simplificare, echivocitate.

Din punctul de vedere al criptanalistului, un sistem de secretizare este aproape identic cu un sistem de comunicatie zgomotos. Mesajul (semnalul transmis) este prelucrat de un element statistic, sistemul de cifrare, cu cheia sa statistic aleasa. Rezultatul acestei operatii este criptograma (analoga cu semnalul perturbat) care este disponibila pentru analiza. Principalele diferente in cele doua cazuri sunt: in primul rand, aceea ca operatia de transformare pentru cifrare este in general de o complexitate mai mare decat zgomotul perturbator intr-un canal; iar in al doilea rand, cheia pentru un sistem de secretizare este de obicei aleasa dintr-un set finit de posibilitati, in timp ce zgomotul dintr-un canal este mai des introdus continuu, practic ales dintr-un set infinit.

Avand in vedere aceste aspecte, este naturala utilizarea echivocitatii ca un index teoretic pentru secretizare. Poate fi observat ca exista doua echivocitati semnificative, aceea a cheii si aceea a mesajului. Acestea vor fi notate prin H_E(K) si respectiv H_E(M). Ele sunt date de:

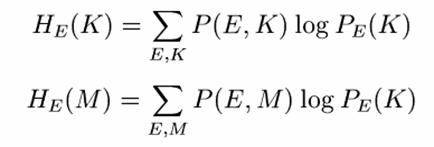
unde E, M si K sunt criptograma, mesajul si cheia, iar

P(E,K) este probabilitatea cheii K si criptogramei E,

P_E(K) este probabilitatea a posteriori a cheii K daca este interceptata criptograma E,

P(E,M) si P_E(M) sunt probabilitatile similare pentru mesaj in locul cheii.

Sumarea din H_E(K) este peste toate criptogramele posibile de o anumita lungime (sa spunem N litere) si peste toate cheile. Pentru H_E(M) sumarea este peste toate mesajele si criptogramele de lungime N. Astfel, H_E(K) si H_E(M) sunt ambele functii de N, numarul de litere interceptate. Acest lucru va fi uneori indicat explicit prin scrierea H_E(K,N) si H_E(M, N). Sa observam ca acestea sunt echivocitati "totale"; adica, nu impartim la N pentru a obtine rata echivocitatii care a fost folosita in MTC.

Aceleasi argumente generale folosite la justificarea echivocitatii ca masura a incertitudinii in teoria comunicatiei se aplica si aici. Sa observam ca echivocitatea zero necesita ca un mesaj (sau cheie) sa aiba probabilitate unitara, toate celelalte zero, corespunzator cunoasterii (informatiilor) complete. Considerata ca o functie de N, descresterea treptata a echivocitatii corespunde cresterii cunoasterii cheii originale a mesajului. Cele doua curbe ale echivocitatii trasate ca functii de N vor fi numite caracteristicile echivocitatii sistemului de secretizare in discutie.

Valorile lui H_E(K,N) si H_E(M, N) pentru criptograma de tip Cezar considerata mai sus au fost calculate si sunt date in ultima linie a Tabelului 1. H_E(K,N) si H_E(M, N) sunt egale in acest caz si sunt date in cifre zecimale (adica, in calcule este folosit logaritmul in baza 10). Ar trebui observat ca aici echivocitatea este pentru o criptograma particulara, sumarea fiind doar peste M (sau K), nu peste E. In general, sumarea ar trebui sa fie peste toate criptogramele posibil interceptate de lungime N si ar trebui sa dea incertitudinea medie. Dificultatile de calcul impiedica aceste calcule generale.

12. PROPRIETATI ALE ECHIVOCITATII

Se poate arata ca echivocitatea are un numar de proprietati interesante, din care cele mai multe se potrivesc cu imaginea noastra intuitiva despre cum ar trebui sa se comporte o astfel de marime. Vom arata mai intai ca echivocitatea cheii sau a unei parti fixe din mesaj descreste atunci cand este interceptat mai mult material cifrat.

Teorema 7. Echivocitatea cheii H_E(K,N) este o functie non-crescatoare de N.

Echivocitatea primelor A litere din mesaj este o functie non-crescatoare de numarul N care a fost interceptat. Daca au fost interceptate N litere din mesaj, echivocitatea primelor N litere din mesaj este mai mica sau egala cu cea a cheii. Acestea se pot scrie astfel:

H_E(K,S) H_E(K,N), S N

H_E(M,S) H_E(M,N), S N (H pentru primele A litere din text)

H_E(M,N) H_E(K,N).

Cerinta privind A litere din al doilea rezultat al teoremei este astfel incat echivocitatea va fi calculata in raport cu cantitatea din mesaj care a fost interceptata. Daca este asa, echivocitatea mesajului poate creste (si de obicei chiar creste) pentru un timp, mai ales datorita faptului ca mai multe litere inlocuiesc o gama posibila mai mare de mesaje. Rezultatele teoremei sunt ceea ce am putea spera de la un index bun de secretizare, din moment ce ne-am astepta foarte greu sa fie mai slab decat media (engl.: we would hardly expect to be worse off on the average), dupa interceptarea de material suplimentar decat inainte. Faptul ca ele pot fi dovedite ofera mai multa justificare pentru a folosi masura echivocitatii.

Rezultatele acestei teoreme sunt consecinta anumitor proprietati ale entropiei conditionate demonstrate in MTC. Astfel, pentru a arata prima sau a doua afirmatie a teoremei 7, avem evenimentele aleatoare A si B,

H(B) H_A(B)

Daca identificam B cu cheia (cunoscand primele S litere din criptograma) si A cu cele N-S litere ramase, obtinem primul rezultat. Similar, identificand B cu mesajul obtinem al doilea rezultat. Ultimul rezultat provine din

H_E(M) H_E(K,M)=H_E(K)+H_E,K(M)

si din faptul ca H_E,K(M)=0, din moment ce K si E determina in mod unic M.

Deoarece mesajul si cheia sunt alese independent, avem:

H(M,K)=H(M)+H(K)

Mai mult,

H(M,K)=H(E,K)=H(E)+H_E(K)

prima egalitate rezultand din faptul ca, cunoasterea lui M si a lui K sau a lui E si a lui K este echivalenta cu cunoasterea tuturor celor trei. Combinand acestea doua, obtinem o formula pentru echivocitatea cheii:

H_E(K)=H(M)+H(K)-H(E)

In particular, daca H(M)=H(E) atunci echivocitatea cheii, H_E(K), este egala cu incertitudinea a priori a cheii, H(K). Acest lucru se intampla in sistemele perfecte descrise mai sus.

O formula pentru echivocitatea mesajului poate fi gasita prin mijloace similare. Avem:

H(M,E)=H(E)+H_E(M)=H(M)+H_M(E)

H_E(M)=H(M)+H_M(E)- H(E).

Daca avem un sistem produs (engl.: product system) S=TR, este de asteptat ca al doilea proces de cifrare sa descreasca echivocitatea mesajului. Ca acest lucru este adevarat, poate fi aratat dupa cum urmeaza: fie M, E₁, E₂ mesajul, respectiv prima si a doua cifrare. Atunci:

P_E1E2(M)=P_E1(M)

Rezulta:

H_E1E2(M)=H_E1(M)

Deoarece, pentru orice variabile aleatoare, x, y, z, H_xy(z) H_y(z), avem rezultatul dorit, H_E2(M) H_E1(M)

Teorema 8. Echivocitatea mesajului intr-un sistem produs S=TR nu este mai mica decat aceea atunci cand este utilizat doar R.

Sa presupunem acum ca avem un sistem T care poate fi scris ca o suma ponderata de mai multe sisteme, R, S, , U:

T=p₁R+p₂S+ +p_mU, Σp_i=1

si ca sistemele R, S, , U au echivocitatile H₁, H₂, H₃, , H_m.

Teorema 9. Echivocitatea H a unei sume ponderate de sisteme este limitata de inegalitatile

Σp_iH_i H Σp_iH_i - Σp_i log p_i .

Acestea sunt cele mai bune limite posibile. H-urile pot fi echivocitati fie ale cheii, fie ale mesajului

Limita superioara este atinsa, de exemplu, in sistemele puternic idealizate (care vor fi descrise mai tarziu), acolo unde descompunerea se face in transformari simple ale sistemului. Limita inferioara se atinge daca toate sistemele R, S, , U intra in spatii complet diferite de criptograme. Aceasta teorema este demonstrata si de inegalitatile generale care guverneaza echivocitatea,

H_A(B) H(B) H(A)+H_A(B)

Identificam A cu sistemul particular care este folosit si B cu cheia sau mesajul.

Exista o teorema similara pentru sumele ponderate ale limbajelor. Pentru aceasta, identificam A cu acel limbaj.

Teorema 10. Sa presupunem ca un sistem poate fi aplicat limbajelor L₁, L₂, , L_m si ca are caracteristicile de echivocitate H₁, H₂, , H_m. Atunci cand se aplica sumei ponderate Sp_iL_i, echivocitatea H este limitata de:

Σp_iH_i H Σp_iH_i - Σp_i log p_i .

Aceste limite sunt maximul posibil, iar echivocitatile in cauza pot fi fie pentru cheie, fie pentru mesaj

Redundanta totala D_N pentru N litere din mesaj este definita prin:

D_N=log G-H(M)

unde G este numarul total de mesaje de lungime N, iar H(M) este incertitudinea in alegerea acestora. Intr-un sistem de secretizare unde numarul total de criptograme posibile este egal cu numarul de mesaje posibile de lungime N, H(E) log G. Rezulta:

H_E(K)=H(K)+H(M)-H(E) H(K)-[log G-H(M)].

Asadar,

H(K)-H_E(K) D_N

Aceasta arata ca, intr-un sistem inchis, de exemplu, micsorarea echivocitatii cheii dupa ce au fost interceptate N litere nu este mai mare decat redundanta a N litere din limbaj. In asemenea sisteme, care cuprind majoritatea cifrurilor (engl.: ciphers), numai existenta redundantei in mesajele originale fac posibila o solutie.

Sa presupunem acum ca avem un sistem pur. Fie diversele clase de reziduuri ale mesajelor C₁, C₂, C₃, , C_r, si fie setul corespunzator de clase de reziduuri ale criptogramelor C , C'₂, C'₃, , C'_r . Probabilitatea fiecarui E din C' este aceeasi:

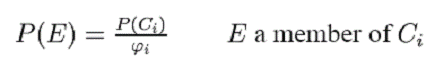
unde j_i este numarul mesajelor diferite din C_i. Astfel, avem:

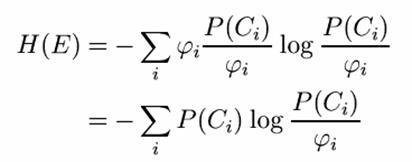
Inlocuind in ecuatia noastra pentru H_E(K), obtinem:

Teorema 11. Pentru un cifru pur,

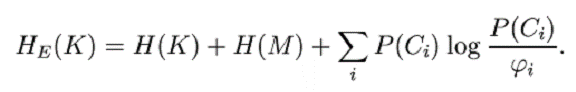
Acest rezultat poate fi folosit pentru a calcula H_E(K) in unele cazuri care prezinta interes.

13. ECHIVOCITATEA PENTRU SUBSTITUTIA SIMPLA PE UN LIMBAJ DE DOUA LITERE

Vom calcula acum echivocitatea cheii sau a mesajului atunci cand este aplicata substitutia simpla pe un limbaj de doua litere, cu probabilitatile p si q pentru 0 si 1, si litere succesive alese independent. Avem:

Probabilitatea ca E sa contina exact s zerouri intr-o anumita permutare este:

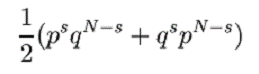
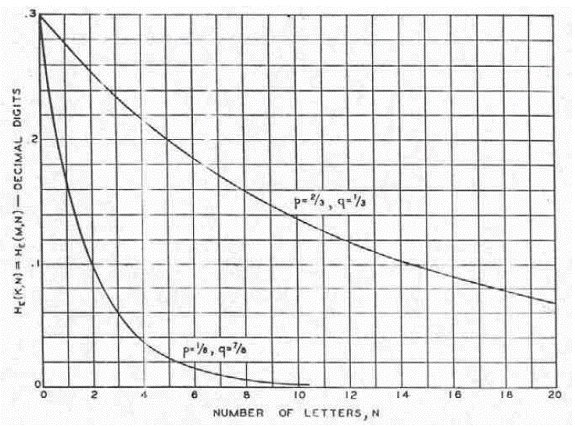
Figura 6. Echivocitatea pentru substitutia simpla pe un limbaj de doua litere

si probabilitatile a posteriori ale substitutiilor identitate si inversiune (singurele doua in sistem) sunt respectiv:

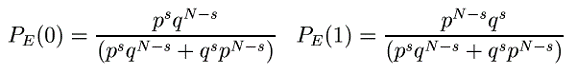
Exista termeni pentru fiecare s, si, astfel:

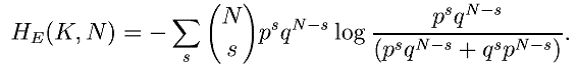
Pentru p=1/3, q=2/3 si pentru p=1/8, q=7/8, H_E(K,N) a fost calculata si este redata in Figura 6.

14. CARACTERISTICA ECHIVOCITATII PENTRU UN CIFRU "ALEATOR"

In sectiunea anterioara am calculat caracteristicile echivocitatii pentru o substitutie simpla aplicata unui limbaj cu doua litere. Acesta este cam cel mai simplu tip de cifru si cea mai simpla structura de limbaj posibila, desi formulele sunt deja destul de complicate, ceea ce le face aproape de neutilizat (engl.: so involved as to be nearly useless). Ce facem cu cazurile de interes practic, sa spunem transformarile implicate de un sistem de transpozitie fractionala aplicate unui text in engleza cu structura sa statistica extrem de complexa? Insasi aceasta complexitate sugereaza o metoda de abordare. Problemele suficient de complicate pot fi rezolvate de multe ori statistic. Pentru a usura acest lucru, definim notiunea de cifru "aleator".

Vom face urmatoarele presupuneri:

1. Numarul de mesaje posibile de lungime N este T=2^R0N, astfel ca R₀=log₂G, unde G este numarul de litere din alfabet. Numarul criptogramelor posibile de lungime N este de asemenea presupus a fi T.

2. Mesajele posibile de lungime N pot fi impartite in doua grupuri: un grup cu probabilitate a priori ridicata si destul de uniforma, al doilea grup cu probabilitate totala neglijabila. Grupul cu probabilitate mare va contine S=2^RN mesaje, unde R=H(M)/N, adica, R este entropia sursei mesajului per litera.

3. Operatia de descifrare poate fi vazuta ca o serie de linii, ca in Figurile 2 si 4, mergand inapoi de la fiecare E catre diverse M-uri. Presupunem k chei echiprobabile diferite in asa fel incat vor fi k linii care duc inapoi de la fiecare E. Pentru cifrul aleator, presupunem ca liniile de la fiecare E se intorc catre o selectie aleatoare de mesaje posibile. De fapt, atunci, un cifru aleator este un intreg ansamblu de cifruri, iar echivocitatea este echivocitatea medie pentru acest ansamblu.

Echivocitatea cheii este definita de

H_E(K)=SP(E)P_E(K)log P_E(K).

Probabilitatea ca exact m linii sa se intoarca de la un anumit E catre grupul de mesaje cu probabilitate mare este

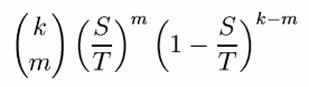
Daca este interceptata o criptograma cu m astfel de linii, echivocitatea este log m. Probabilitatea unei astfel de criptograme este mT/SK, deoarece poate fi produsa de m chei din mesajele de probabilitate mare, fiecare cu probabilitatea T/S. De aici, echivocitatea este:

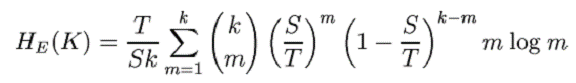
Dorim sa gasim o aproximare simpla pentru aceasta atunci cand k este mare. Daca valoarea care este de asteptat sa apara a lui m, adica , variatia lui log m peste domeniul unde distributia binomiala presupune valori mari va fi mica, si putem inlocui log m cu log . Acesta poate fi acum scos ca factor comun din sumare (engl.: can now be factored out of the summation), ceea ce se reduce apoi la . De aici, cu aceasta conditie,

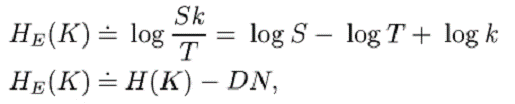
unde D este redundanta per litera din limbajul original (D=D_N/N).

Daca este mic in comparatie cu marele k, distributia binomiala poate fi aproximata printr-o distributie Poisson:

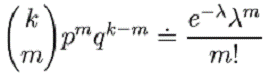
unde l=Sk/T. De aici,

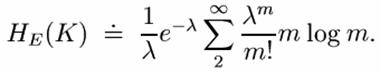
Daca inlocuim m cu m+1, obtinem:

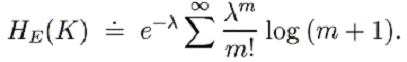
Acest lucru poate fi utilizat in zona unde l este aproape unitar. Pentru l<<1, singurul termen important din serie este cel pentru m=1; neglijandu-i pe ceilalti, avem:

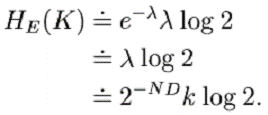
Pentru a concluziona: H_E(K), considerata ca functie de N, numarul de litere interceptate, porneste de la H(K) atunci cand N=0. Ea descreste liniar cu o panta -D afara din vecinatatea lui N=H(K)/D. Dupa o regiune scurta de tranzitie, H_E(K) urmeaza o exponentiala cu distanta de injumatatire (engl.: "half life" distance) 1/D, daca D este masurata in biti per litera. Acest comportament este prezentat in Figura 7, impreuna cu curbele aproximative.

Dintr-un motiv similar poate fi calculata echivocitatea mesajului. Ea este:

H_E(M)=R₀N, pentru R₀N << H_E(K)

H_E(M)= H_E(K), pentru R₀N >> H_E(K)

H_E(M)= H_E(K)-φ(N), pentru R₀N ~ H_E(K)

unde j(N) este functia prezentata in Figura 7 cu scala N redusa cu un factor D/R₀. Astfel, H_E(M) creste liniar cu panta R₀, pana cand aproape intersecteaza linia H_E(K).

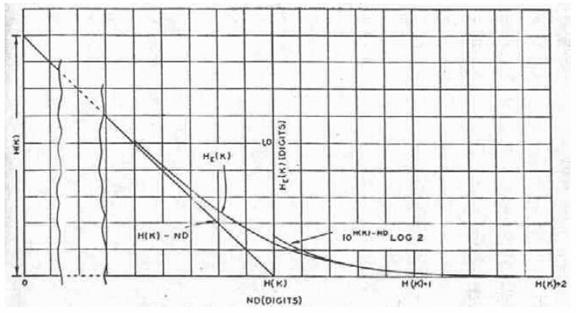
Figura 7. Echivocitatea pentru cifrul aleator

Dupa o tranzitie completa (engl.: rounded transition) ea urmeaza in jos curba H_E(K).

Se va vedea din Figura 7 ca, curbele echivocitatii tind catre zero destul de abrupt. Astfel putem vorbi, cu doar o mica ambiguitate, despre un punct in care solutia devine unica. Pentru cifrul aleator, acesta este aproximativ H(K)/D.

15. APLICATIE LA CIFRURILE STANDARD

Cele mai multe din cifrurile standard implica operatii de cifrare si descifrare destul de complicate. Mai mult, este extrem de implicata structura statistica a limbajelor naturale. Este deci rezonabil sa presupunem ca formulele derivate din cifrul aleator pot fi aplicate in asemenea cazuri. Este totusi necesar sa aplicam anumite corectii in unele cazuri. Principalele puncte care trebuie observate sunt urmatoarele:

1. Am presupus pentru cifrul aleator ca descifrarile posibile ale criptogramei sunt o selectie aleatoare din mesajele posibile. Desi nu este strict adevarat in sistemele obisnuite, acest caz apare din ce in ce mai mult / acesta devine mai apropiat de adevar (engl.: "this becomes more nearly the case"), pe masura ce creste complexitatea operatiilor de cifrare si a structurii limbajului. Cu un cifru de transpozitie este clar ca frecventele literelor sunt pastrate sub operatiile de descifrare. Aceasta inseamna ca descifrarile posibile sunt alese dintr-un grup mai limitat, nu din intregul spatiu de mesaje, iar formula ar trebui schimbata. In locul lui R₀, se poate utiliza R₁, rata entropiei pentru un limbaj cu litere independente dar cu frecvente regulate ale literelor. In alte cateva cazuri, poate fi vazuta o tendinta definita catre intoarcerea descifrarilor catre mesajele cu probabilitate mare. Daca nu exista o tendinta clara a acestui tip, iar sistemul este suficient de complicat, atunci este rezonabil sa se utilizeze analiza cifrului aleator.

2. In multe cazuri, nu este utilizata cheia completa in cifrarea mesajelor scurte. De exemplu, intr-o substitutie simpla, numai mesajele suficient de lungi vor contine toate literele alfabetului si astfel implica cheia completa. Este evident ca presupunerea aleatoare nu se mentine pentru N mic intr-un astfel de caz, din moment ce toate cheile care difera doar prin literele care nu apar inca in criptograma conduc inapoi catre acelasi mesaj si nu sunt distribuite aleator. Aceasta eroare este corectata usor catre o aproximare buna prin utilizarea unei "caracteristici de aparitie a cheii". Cineva utilizeaza, pentru un anumit N, cantitatea efectiva din cheie la care ne putem astepta cu acea lungime a criptogramei. Pentru cele mai multe cifruri, acest lucru este usor de estimat.

3. Exista anumite "efecte de sfarsit" din cauza initializarii definite a mesajului, care produc o discrepanta fata de caracteristicile aleatoare. Daca luam un punct de initializare aleator intr-un text in engleza, prima litera (atunci cand nu observam literele precedente) are o posibilitate de a fi orice litera, cu probabilitatile obisnuite ale literelor. Urmatoarea litera este specificata mai complet din moment ce avem apoi frecventele din diagrama. Aceasta micsorare a valorii de alegere continua pentru un timp. Efectul acestui lucru asupra curbei este ca portiunea de linie dreapta este mutata si apropiata de o curba care depinde de cat de mult este imprastiata structura statistica a limbajului peste literele vecine. Ca o prima aproximare, curba poate fi corectata prin translatia liniei catre punctul de jumatate de redundanta (engl.: "half redundancy point") - adica, numarul de litere unde redundanta limbajului este jumatate din valoarea sa finala.

Daca se iau in calcul aceste trei efecte, pot fi facute estimari rezonabile ale caracteristicii echivocitatii si ale punctului de unicitate. Calculele pot fi facute grafic, asa cum este indicat in Figura 8. Se traseaza caracteristica aparitiei cheii si curba pentru redundanta totala D_N (care este de obicei suficient de bine reprezentata prin linia N D ). Diferenta dintre acestea, catre vecinatatea intersectiei lor este H_E(M). Cu un cifru simplu de substitutie aplicat textului in engleza, aceste calcule au dat curbele prezentate in Figura 9. caracteristica aparitiei cheii a fost in acest caz estimata prin numararea literelor diferite care apar in portiunile tipice in engleza de N litere. Cat timp au putut fi gasite date experimentale pe substitutia simpla, ele se potrivesc suficient de bine cu curbele din Figura 9, luand in considerare diversele idealizari si aproximari care au fost facute. De exemplu, poate fi demonstrat experimental ca punctul de unicitate, situat la aproximativ 27 de litere, se gaseste intre limitele 20 si 30. Cu 30 de litere exista aproape intotdeauna o solutie unica la o criptograma de acest tip, iar cu 20 este de obicei usor de gasit un numar de solutii.

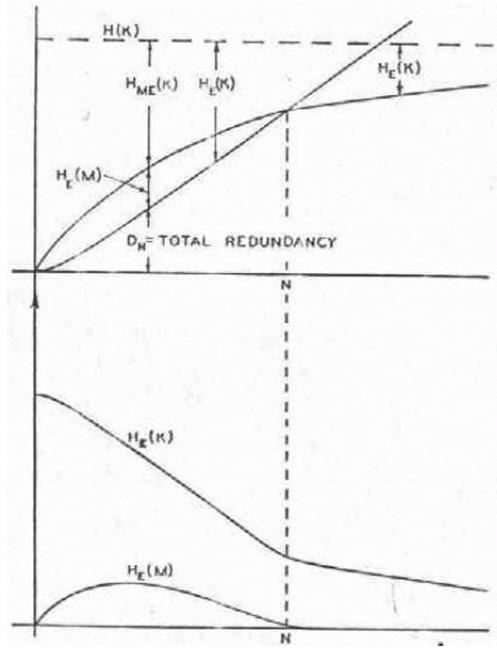
Figura 8. Calculul grafic al echivocitatii

Cu o transpozitie cu perioada d (cheie aleatoare), H(K)=log d!, sau aproximativ d log d/e (folosind o aproximare Stirling pentru d!). Daca luam 0,6 cifre zecimale per litera ca redundanta potrivita, reamintindu-ne de pastrarea frecventei literelor, obtinem aproximativ 1,7d log d/e ca distanta de unicitate. Aceasta se verifica de asemenea destul de bine experimental. Sa observam ca in acest caz H_E(M) este definit numai pentru multipli intregi ai lui d.

Cu Vigenère, punctul de unicitate va aparea la aproximativ 2d litere, si de asemenea acest lucru este aproape adevarat. Caracteristica Vigenère de aceeasi dimensiune a cheii ca si substitutia simpla va fi aproximativ aceeasi cu cea prezentata in Figura 10. Cazurile Vigenère, Playfair si Fractional au sanse mai mari corespunda formulelor teoretice pentru cifruri aleatoare decat substitutia simpla si transpozitia. Motivul acestui lucru este ca ele sunt mai complexe si dau caracteristici de mixare mai bune mesajelor pe care opereaza.

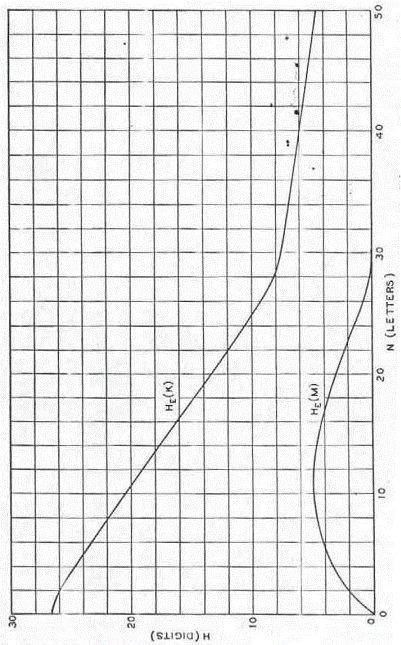
Figura 9. Echivocitatea pentru substitutia simpla in engleza

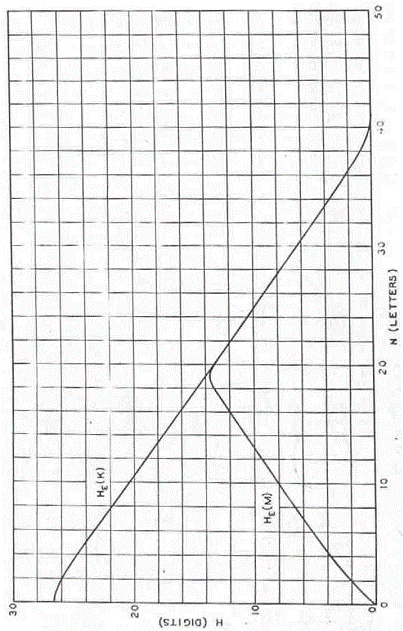
Figura 10. Echivocitatea pentru Vigenère in engleza

Alfabetul mixat Vigenère (fiecare din cele d alfabete mixate independent si folosite secvential) are o dimensiune a cheii

H(K)=d log 26!=26,3d

iar punctul de unicitate ar trebui sa fie la aproximativ 53d litere.

Aceste concluzii pot fi de asemenea introduse intr-un test experimental cu cifrul de tip Cezar. Intr-o anumita criptograma analizata in Tabela 1, sectiunea 11, functia H_E(K,N) a fost calculata si este data mai jos, impreuna cu valorile pentru un cifru aleator.

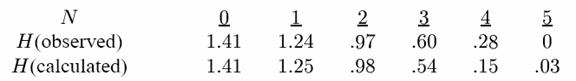
Se vede ca potrivirea este destul de buna, mai ales cand ne amintim ca H observata ar trebui de fapt sa fie media mai multor criptograme diferite, si ca H pentru valori mari ale lui N este estimat doar grosier.

Se mai vede ca analiza cifrului aleator poate fi folosita pentru a estima caracteristicile echivocitatii si distanta de unicitate pentru tipurile obisnuite de cifruri.

16. VALIDITATEA UNEI SOLUTII PENTRU CRIPTOGRAMA

Formulele pentru echivocitate sunt relevante pentru intrebarile care apar uneori in munca criptografica privind validitatea unei pretinse solutii la o criptograma. In istoria criptografiei au existat multe criptograme, sau posibile criptograme, la care analisti inteligenti au gasit o "solutie". Acest lucru a implicat totusi un proces asa de complex, sau materialul a fost asa de sarac, incat s-a nascut intrebarea daca criptanalistii au "citit solutia" in criptograma. Vezi, de exemplu, cifrurile Bacon-Shakespeare si manuscrisul "Roger Bacon" (NOTA: Vezi Fletcher Pratt, loc. cit.).

In general, putem spune ca daca un sistem si o cheie propuse rezolva o criptograma pentru o marime a materialului considerabil mai mare decat distanta de unicitate, solutia este destul de suspecta.

Acest efect al redundantei in producerea treptata a solutiei unice pentru un cifru poate fi vazuta si in alt mod, ceea ce este de ajutor. Redundanta este in esenta o serie de conditii peste literele mesajului, care asigura ca va fi rezonabil statistic. Aceste conditii de consistenta produc conditii de consistenta corespunzatoare in criptograma. Cheia ofera o anumita masura de libertate pentru criptograma, dar, pe masura ce sunt interceptate tot mai multe litere, conditiile de consistenta epuizeaza libertatea permisa de cheie. In final, exista un singur mesaj si o singura cheie care satisfac toate conditiile si au o solutie unica. In cifrul aleator, conditiile de consistenta sunt, intr-un sens "ortogonal" cu "granularitatea cheii" si isi au efectul complet in eliminarea mesajelor si cheilor cat de repede posibil. Acesta este cazul obisnuit. Totusi, prin proiectare corespunzatoare, este posibil sa se "aranjeze" redundanta limbajului cu "granularitatea cheii" in asa fel incat conditiile de consistenta sa fie automat satisfacute si H_E(K) sa nu se apropie de zero. Aceste sisteme "ideale", care vor fi luate in considerare in urmatoarea sectiune, sunt de asa natura incat toate transformarile T_i induc aceleasi probabilitati in spatiul E.

17. SISTEME DE SECRETIZARE IDEALE

Am vazut ca secretizarea perfecta necesita o cantitate infinita din cheie daca permitem mesaje de lungime nelimitata. Cu o dimensiune finita a cheii, echivocitatea cheii si a mesajului se apropie in general de zero, dar nu in mod necesar. De fapt, este posibil ca H_E­(K) sa ramana constant la valoarea sa initiala H(K). Apoi, indiferent de cat de mult material este interceptat, nu exista o solutie unica, cu mai multe, cu probabilitati comparabile. Am definit un sistem "ideal" ca fiind unul in care H_E­(K) si H_E­(M) nu tind la zero pentru N ∞. Un sistem "puternic ideal" este unul in care ca H_E­(K) ramane constant H(K).

Un exemplu este substitutia simpla pe un limbaj artificial in care toate literele sunt echiprobabile, iar literele succesive sunt alese independent. Este usor de vazut ca H_E­(K)=H(K), iar H_E­(M) creste liniar de-a lungul unei linii de panta log G (unde G este numarul de litere din alfabet) pana cand atinge linia H(K), dupa care ramane constant la aceasta valoare.

Cu limbajele naturale este in general posibila aproximarea caracteristicii ideale - punctul de unicitate poate fi facut sa apara pentru N oricat de mare. Totusi, complexitatea sistemului necesar creste de obicei rapid cand incercam acest lucru. Nu este intotdeauna posibila atingerea efectiva a caracteristicii ideale cu orice sistem de complexitate finita.

Pentru a aproxima echivocitatea ideala, se poate opera mai intai pe mesaj cu un transformator (engl.: transducer) care inlatura toate redundantele. Dupa aceasta, aproape orice sistem de cifrare simplu - substitutie, transpozitie, Vigenère etc. - este satisfacator. Cu cat transformatorul este mai elaborat iar iesirea este mai aproape de forma dorita, cu atat mai bine sistemul de secretizare va aproxima caracteristica ideala.

Teorema 12. O conditie necesara si suficienta pentru ca T sa fie puternic ideal este ca, pentru oricare doua chei, T_i^-1T_j sa fie o transformare care pastreaza masurile, de pe spatiul mesaj catre el insusi.

Acest lucru este adevarat din moment ce probabilitatea a posteriori a fiecarei chei este egala cu probabilitatea sa a priori daca si numai daca aceasta conditie este satisfacuta.

18. EXEMPLE DE SISTEME DE SECRETIZARE IDEALE

Sa presupunem ca limbajul nostru consta intr-o secventa de litere, toate alese independent si cu probabilitati egale. Atunci redundanta este zero, iar din rezultatul de la sectiunea 12, H_E(K)=H(K). Obtinem rezultatul:

Teorema 13. Daca toate literele sunt echiprobabile si independente, orice cifru inchis este ideal.

Echivocitatea mesajului va creste de-a lungul caracteristicii aparitiei cheii, care se va apropia de obicei de H(K), desi in unele cazuri nu. In cazurile substitutiei pe n-grame, transpozitiei, Vigenère, si variatiilor, fractiilor etc., avem sisteme puternic ideale pentru acest limbaj simplu cu H_E(M) H(K), pentru N

Sistemele de secretizare ideale sufera de un numar de dezavantaje.

1. Sistemul trebuie sa se potriveasca foarte bine cu limbajul. Aceasta necesita un studiu extensiv al structurii limbajului, de catre proiectant. De asemenea, o modificare in structura statistica sau o selectie din setul de mesaje posibile, ca in cazul cuvintelor probabile (cuvinte care sunt de asteptat sa apara in aceasta criptograma), fac ca sistemul sa fie vulnerabil la analiza.

2. Structura limbajelor naturale este extrem de complicata, iar acest lucru implica o complexitate a transformarilor necesare pentru a elimina redundanta. Astfel, orice masina care trebuie sa efectueze aceasta operatie trebuie in mod necesar sa fie destul de complicata, cel putin in sensul stocarii informatiilor, din moment ce trebuie sa ne asteptam la un "dictionar" al magnitudinii mai mare decat cea a unui dictionar obisnuit.

3. In general, transformarile necesare introduc o propagare defectuoasa a caracteristicii erorii. O eroare in transmisia unei singure litere produce o regiune de modificari langa ea, de marime comparabila cu lungimea efectelor statistice in limbajul original.

19. OBSERVATII MAI PROFUNDE ASUPRA ECHIVOCITATII SI REDUNDANTEI

Am considerat redundanta "englezei normale" ca fiind aproximativ 0,7 cifre zecimale per litera, sau o redundanta de 50%. Aceasta este pe baza ipotezei ca au fost omise despartirile in silabe ale cuvintelor (engl.: word divisions). Este o cifra aproximativa, bazata pe o structura statistica extinsa pe aproximativ 8 litere, si considera textul ca fiind unul de tip obisnuit, cum ar fi scriere de ziar, text literar etc. Putem observa aici o metoda de estimare grosiera a acestui numar care este de un oarecare interes criptografic.

Un cifru cu cheie succesiva (engl.: running key) este un sistem de tip Vernam unde, in locul unei secvente aleatoare de litere, cheia este un text cu inteles. Acum este cunoscut faptul ca cifrurile cu cheie succesiva pot fi de obicei rezolvate unic. Acest lucru arata ca engleza poate fi redusa cu un factor de doi la unu si implica o redundanta de cel putin 50%. Aceasta cifra nu poate fi marita foarte mult, totusi, pentru un numar de motive, in afara cazului in care este luata in considerare structura cu "inteles" de arie larga (engl.: long range "meaning") a englezei.

Cifrul cu cheie succesiva poate fi usor imbunatatit spre sisteme de cifrare care nu pot fi rezolvate fara cheie. Daca se foloseste in loc de un text in engleza, aproximativ d texte diferite drept cheie, adaugandu-le pe toate mesajului, o cantitate suficienta din cheie a fost introdusa pentru a produce o echivocitate mare si pozitiva. O alta metoda ar fi sa se utilizeze, sa spunem, fiecare a 10-a litera din text ca si cheie. Literele intermediare sunt omise si nu mai pot fi folosite in nici un alt punct al mesajului. Acest lucru ale cam acelasi efect, din moment ce aceste litere distantate sunt aproape independente.

Faptul ca vocalele dintr-un pasaj pot fi omise fara o pierdere semnificativa sugereaza o cale simpla de imbunatatire substantiala a aproape oricarui sistem de cifrare. Mai intai se sterg toate vocalele, sau tot atat de mult din mesaje cat este posibil fara sa se ajunga la riscul reconstructiilor multiple, si apoi se cifreaza ceea ce ramane. Din moment ce acest lucru reduce redundanta cu un factor de poate 3 sau 4 la 1, punctul de unicitate va fi eliminat de acest factor. Acesta este unul din caile de abordare a sistemelor ideale - folosind cunostintele de engleza ale descifratorului ca parte in sistemul de descifrare.

20. DISTRIBUTIA ECHIVOCITATII

O descriere mai completa a sistemului de secretizare aplicat unui limbaj pe care caracteristicile echivocitatii si-l pot permite poate fi gasita prin introducerea distributiei echivocitatii. Pentru N litere interceptate consideram fractia din criptograme pentru care echivocitatea (pentru aceste E-uri, nu media H_E(M)) ia valori intre anumite limite. Acest lucru da o functie de distributie a densitatii:

P(H_E(M),N) dH_E(M)

pentru probabilitatea ca pentru N litere H sa se gaseasca intre limitele H si H+dH. Media echivocitatii pe care am studiat-o mai devreme este media acestei distributii. Functia P(H_E(M),N) poate fi vazuta trasata de-a lungul unei a treia dimensiuni, normala pe planul foii, pe planul H_E(M),N. Daca limbajul este pur, cu o arie de influenta redusa, iar cifrul este pur, functia va fi de obicei o muchie in acest plan, al carei punct maxim urmareste aproximativ media H_E(M), cel putin pana langa punctul de unicitate. In acest caz, sau atunci cand conditiile sunt aproape verificate, curba medie ofera o imagine rezonabil de completa asupra sistemului.

Pe de alta parte, daca limbajul nu este pur, dar alcatuit dintr-un set de componente pure

L=Σp_iL_i

avand diferite curbe de echivocitate cu sistemul, atunci distributia totala va fi de obicei alcatuita dintr-o serie de muchii. Va exista cate una pentru fiecare L_i ponderata corespunzator cu p_i-ul sau. Caracteristica echivocitatii medii va fi o linie undeva intre aceste muchii, si poate sa nu ofere o imagine foarte completa a situatiei. Acest lucru este prezentat in Figura 11. Un efect similar are loc daca sistemul nu este pur, ci alcatuit din cateva sisteme cu curbe H diferite.

Efectul mixarii limbajelor pure, apropiate unele de altele ca structura statistica, este cresterea latimii muchiei.

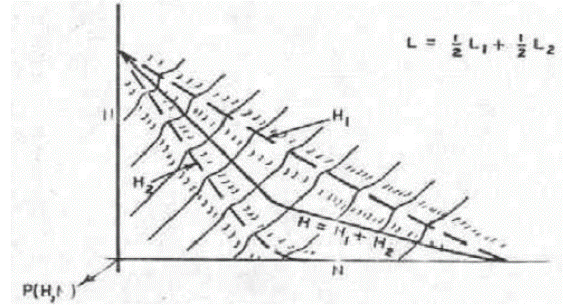
Figura 11. Distributia echivocitatii cu un limbaj mixat L-1/2L₁+1/2L₂

Langa punctul de unicitate, aceasta tinde sa mareasca echivocitatea, din moment ce echivocitatea nu poate deveni negativa, iar imprastierea este in special in directie pozitiva. Ne asteptam deci ca in aceasta regiune calculele bazate pe cifrul aleator sa fie oarecum reduse.

PARTEA A III-A

SECRETIZAREA PRACTICA

21. CARACTERISTICA DE LUCRU

Dupa ce a fost depasit punctul de unicitate in materialul interceptat, va exista de obicei o solutie unica la criptograma. Problema izolarii acestei singure solutii de probabilitate ridicata este problema criptanalizei. In regiunea dinaintea punctului de unicitate putem spune ca problema criptanalizei este aceea de a izola toate posibilele solutii de probabilitate ridicata (in comparatie cu ceea ce ramane) si de a determina diversele lor probabilitati.

Desi este intotdeauna posibila in principiu determinarea acestor solutii (prin incercarea fiecarei chei posibile, de exemplu), sisteme de cifrare diferite prezinta o variatie larga in volumul de lucru necesar. Volumul mediu de lucru pentru a determina cheia unei criptograme de N litere, W(N), masurata sa spunem in om-ore, poate fi denumita caracteristica de lucru a sistemului. Aceasta medie este luata peste toate mesajele si toate cheile cu probabilitatile lor corespunzatoare. Functia W(N) este o masura a cantitatii de "secretizare practica" pe care si-o poate permite sistemul.

Pentru o substitutie simpla in engleza, caracteristica de lucru si cea a echivocitatii vor arata cumva ca in Figura 12. portiunea punctata a curbei este in zona unde exista numeroase solutii posibile, iar acestea trebuie toate determinate.

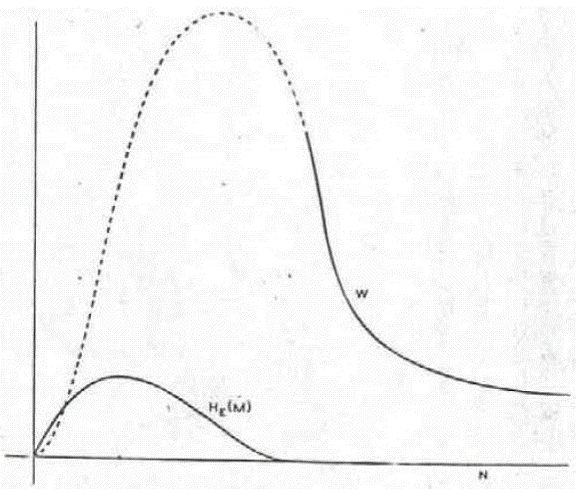
Figura 12. Caracteristicile tipice pentru volumul de lucru si pentru echivocitate

In portiunea continua, dupa punctul de unicitate, in general exista o singura solutie, dar, daca numai datele minim necesare sunt furnizate, este nevoie de un volum foarte mare de lucru pentru a o izola. Pe masura ce este disponibil mai mult material, volumul de lucru scade rapid catre o valoare asimptotica - unde datele suplimentare nu mai reduc volumul de lucru.

In esenta, comportamentul prezentat in Figura 12 este de asteptat sa apara cu orice tip de sistem de secretizare unde echivocitatea se apropie de zero. Scala de om-ore necesara, totusi, va diferi mult cu tipuri diferite de cifruri, chiar si atunci cand curbele H_E(M) sunt aproape identice. Un Vigenère sau un Vigenère compus, de exemplu, cu aceeasi marime a cheii ar trebui sa aiba o caracteristica de lucru mult mai buna (de exemplu, mult mai ridicata). Un sistem (practic) de secretizare bun este unul in care curba W(N) ramane suficient de ridicata, pana spre numarul de litere care se asteapta a fi transmise cu cheia, pentru a impiedica inamicul sa ajunga de fapt la solutie, sau sa intarzie acest lucru pana spre o limita la care informatiile sunt deja perimate (inutile, in plus).

Vom considera in sectiunea urmatoare modalitatile de a pastra functia W(N) mare, chiar daca H_E(K) poate fi practic zero. Acestea este in esenta un tip de problema "max min" asa cum se intampla intotdeuna in cazul luptei intelectelor¹²????. In proiectarea unui bun cifru trebuie maximizat minimul cantitatii de efort pe care inamicul trebuie sa-l depuna pentru a sparge cifrul. Nu este suficient sa ne asiguram ca nu exista metode standard ale muncii criptanalistului - trebuie sa fim siguri ca nu exista nici o metoda care sa sparga usor sistemul. Aceasta, de fapt, a fost slabiciunea multor sisteme; desi proiectate sa reziste tuturor metodelor cunocute, mai tarziu, s-au dovedit vulnerabile in fata noilor tehnici de criptanaliza.

Problema unui cifru bun este aceea de a gasi problemele dificile, subiect al altor conditii sigure. Aceasta este o situatie rar intalnita, deoarece se cauta, in general, problemele cu solutiile cele mai simple si usoare.

Cum putem fi vreodata siguri ca un sistem care nu este ideal si care are o solutie unica pentru un N suficient de mare va necesita un volum mare de munca pentru a fi spart cu fiecare metoda de analiza? Exista doua abordari la aceasta problema; (1) Putem studia metodele posibile ale solutiei disponibile criptanalistului si sa incercam sa le descriem in termeni suficient de generali pentru a acoperi orice metoda pe care el ar putea sa o foloseasca. Apoi, vom construi sistemul nostru care sa reziste acestei metode generale de solutionare. (2) Putem construi cifrul nostru astfel incat spargerea lui este echivalenta cu (sau necesita intr-un anumit moment de timp al procesului) solutionarea unei probleme care se stie ca este foarte laborioasa. Astfel, daca putem arata ca rezolvarea unui sistem sigur necesita o munca cel putin egala cu cea depusa pentru solutionarea unui sistem de ecuatii simultane cu un numar mare de necunoscute, complexe, atunci vom avea o banda joasa a tipurilor pentru caracteristica de lucru.

Urmatoarele trei sectiuni prezinta aceste probleme generale. Este dificil sa definesti idei pertinente care presupun suficienta precizie, pentru a obtine rezultate sub forma unor teoreme matematice. Se considera insa, ca respectivele concluzii, sub forma unor principii generale, sunt corecte.

22. Generalitati in privinta solutionarii criptogramelor

Dupa ce distanta unica a fost depasita in materialul interceptat, orice sistem poate fi solutionat, in principiu, prin a incerca fiecare cheie posibila, pana cand este obtinuta solutia unica - astfel incat, mesajul descifrat are sens in limbajul original. Un calcul simplu arata ca aceasta metoda de solutionare (care poate fi numita trial complet si eroare) nu este aplicabila decat atunci cand cheia este absurd de mica.

Sa presupunem ca, de exemplu, avem o cheie cu 26! posibilitati sau cu aproximativ 26.3 digiti zecimali, aceeasi dimensiune ca in substitutia simpla in limba engleza. Aceasta este, intr-o masura semnificativa, o cheie mica. Ea poate fi scrisa pe o bucata mica de hartie sau memorata in cateva minute. Poate fi inregistrata pe 27 de switch-uri, fiecare avand 10 pozitii sau pe 88 switch-uri cu doua pozitii.

Mai departe, presupunem ca un criptanalist are toate avantajele posibile si construieste un device (dispozitiv) electronic care sa testeze (incerce) cheile la o rata de o microsecunda (poate in mod automat sa selecteze din rezultatele testului pentru semnificatie statistica). El se poate astepta sa gaseasca o cheie corespunzatoare dupa parcurgerea a jumate din cale si dupa un timp estimat de aproximativ

ani.

Cu alte cuvinte, chiar si cu o cheie mica, trialul (testul) si eroarea (complete) nu va fi niciodata folosit la solutionarea criptogramelor, cu exceptia cazurilor triviale in care cheia este extrem de mica, de ex. cifrul Cezar cu 26 posibilitati sau 1.4 digiti. Metoda trialului si erorii, care este folosita atat de des in criptografie este de un alt tip sau este extinsa prin alte mijloace. Daca avem un sistem secretizat care necesita trialul si eroarea complete, el va fi extrem de sigur. Un astfel de sistem va rezulta, se pare, daca mesajele originale cu inteles, sa spunem din 1000 litere, reprezinta selectii aleatoare din setul tuturor secventelor de 1000 de litere. Daca oricare dintre cifrurile aleatoare care au fost aplicate acestui tip de limbaj pare a fi o mica imbunatatire a trialului si erori complete, poate fi posibil.

Metodele de criptanaliza folosite in prezent implica de cele mai multe ori trialul (test) si eroarea, dar in diferite moduri. Pentru inceput, trialurile au evoluat de la ipotezele mai probabile la cele mai putin probabile, iar in al doilea rand, fiecare trial dispune de un numar mare de chei, nu doar de una singura. Astfel, spatiul cheii poate fi impartit in 10 subseturi, fiecare continand aproximativ acelasi numar de chei. Din cel mult 10 trialuri, unul determina care dintre subseturi este cel corect. Acest subset este apoi divizat in cateva subseturi secundare si procesul se repeta. Cu aceeasi dimensiune a cheii (26!=2*10²⁵) ne vom astepta la aproximativ 26*5 sau 130 trial-uri (teste) comparate cu 10²⁶ de trialul si eroarea complete. Posibilitatea de a alege cel mai potrivit dintre subseturi primul pentru test, va imbunatati acest rezultat si mai mult. Daca impartirile au fost facute intre doua sectiuni (cea mai buna cale de a minimiza numarul de teste, trial-uri) doar 88 de teste vor fi necesare. Cat timp trial-ul si eroarea complete vor solicita trial-uri in ordinea numarului cheilor, aceasta subdivizare de test si eroare va solicita doar trial-uri in ordinea dimensiunii cheii in biti.

Aceasta ramane adevarata chiar si atunci cand chei diferite au diferite probabilitati. Atunci, procedura corespunzatoare de a minimiza numarul asteptat de teste (trial-uri) este aceea de a imparti spatiul cheii in subseturi de echiprobabilitati. Cand este determinat subsetul corespunzator, acesta este din nou subivizat in subseturi de echiprobabilitati. Daca acest proces poate fi continuat, numarul de teste asteptat cand fiecare diviziune este reprezentata de doua subseturi, va fi:

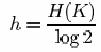
Daca fiecare test are S rezultate posibile si fiecare dintre acestea corespunde cheii aflate intr-unul dintre subseturile de echiprobabilitati S, atunci:

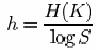
trial-uri vor fi asteptate. Semnificatia intuitiva a acestor rezultate ar trebui notata. Intr-un test cu doua sectiuni cu echiprobabilitate, fiecare test furnizeaza un bit de informatie drept cheie. Daca subseturile au diferite probabilitati, ca in testarea unei singure chei in trial-ul si eroarea complete, doar o mica parte din informatie este obtinuta din test. Astfel, cu 26 chei echiprobabile, testarea uneia furnizeaza doar:

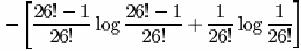
sau aproximativ 10^-25 biti de informatie.

Impartirea in S subseturi de echiprobabilitati maximizeaza informatia obtinuta din fiecare trial, la logS, iar numarul asteptat de trial-uri reprezinta informatia totala ce este obtinuta, care este H(K), impartita la aceasta cantitate.

Problema aici este similara cu cea a monedelor de diferita greutate care a circulat recent. Un exemplu tipic este urmatorul: se stie ca o moneda din 27 este contrafacuta si mult mai stralucitoare decat celelalte. Balanta chimistului este disponbila si moneda contrafacuta va fi izolata de celelalte, printr-o serie de cantariri. Care este numarul minim de cantariri necesare? Raspunsul corect este 3, obtint, la inceput, prin impartirea monedelor in trei grupuri de cate 9 monede fiecare. Doua dintre acestea sunt comparate in balanta. Trei rezultate posibile determina setul de 9 care contine moneda contrafacuta. Acest set este apoi divizat in 3 subseturi de cate 3 fiecare, iar proceesul continua. Setul de monede corespunde setului cheilor, moneda contrafacuta corespunde cheii corecte, iar procedura de cantarire este trial-ul sau testul. Incertitudinea initiala este de log₂27 biti, iar fiecare trial furnizeaza log₂3 biti de informatie; astfel, cand nu este "problema ????" (eng.:"diophantine trouble"),

sau 3 trial-uri sunt suficiente.

Aceasta metoda de solutionare este viabila doar daca spatiul cheii poate fi impartit intr-un numar mic de subseturi, cu o metoda simpla de determinare a subsetului caruia ii apartine cheia corecta. Poate fi testata o metoda care nu are nevoie sa-si asume o cheie completa, in sensul aplicarii unui test de consistenta si determinarii justificarii presupunerii - presupunerea pentru o parte din cheie (sau daca respectiva cheie este intr-o sectiune mare din spatiul cheii). Cu alte cuvinte, este posibil sa se rezolve cheia bit cu bit.

Posibilitatea unei astfel de metode de analiza reprezinta slabiciunea de baza a celor mai multe sisteme de cifrare. De exemplu, in substitutia simpla, o presupunere pentru o singura litera poate fi verificata pentru frecventa sa, varietatea contactului, dublelor sau reversurilor, etc. La determinarea unei singure litere, spatiul cheii este redus prin 1.4 digiti zecimali din initialul 26. Acelasi efect este vazut in toate tipurile elementare de cifruri. In Vigenere, presupunerea a doua sau trei litere ale cheii este verificata usor prin descifrarea la alte puncte cu acest fragment si notarea, daca apare clarul. Vigenere compus este mult mai bun, din acest punct de vedere, daca presupunem un numar mare de perioade componente, care produc o rata de repetitie mai mare decat va fi interceptata. In acest caz, sunt folosite in cifrare atatea litere cheie cate perioade exista pentru fiecare litera. Desi aceasta este doar ofractiune din intreaga cheie, cel putin un numar corect de litere trebuie presupus, inainte ca verificarea consistentei sa poata fi aplicata.

Prima noastra concluzie este atunci, privind proiectarea cifrurilor cu cheie mica, ca ar trebui utilizata o cantitate considerabila a cheii la cifrarea fiecarui element mic din mesaj.

23. METODE STATISTICE

Este posibil sa fie rezolvate multe tipuri de cifruri prin analiza statistica. Vom considera din nou substitutia simpla. Primul lucru pe care il face un criptanalist cu o criptograma interceptata este acela de a face o masurare a frecventei. Daca respectiva criptograma contine, sa spunem, 200 de litere, este sigur sa se presupuna ca o parte din litere sunt in afara grupurilor lor de frecventa, aceasta fiind o impartire in 4 seturi de limite de frecventa bine definite. Logaritmul numarului de chei, cu aceasta limitare poate fi calculata ca:

si frecventa simpla conduce la reducerea incertitudinii cheii prin 12 digiti zecimali, un extraordinar castig.

In general, un atac statistic decurge dupa cum urmeaza: O statistica (valoare) sigura este masurata pe o criptograma interceptata E. Aceasta statistica este la fel pentru toate mesajele rezonabile M si se presupune ca are aceeasi valoare, S_k, valoarea depinzand doar de cheia particulara K ce este folosita. Valoarea astfel obtinuta serveste la limitarea cheilor posibile la acele chei care furnizeaza valori ale lui S in vecinatatea celei observate. O statistica ce nu depinde de K sau care variaza cu M, cat variaza cu K nu este o valoare in limita lui K. Astfel, in cifrurile de transpozitie, frecventa masurata a literelor nu da nici o informatie despre K - fiecare K pastreaza statistica aceeasi. De aceea, una care nu este de folos in frecventa, conteaza in spargerea cifrurilor de transpozitie.

Mai precis, una care atribuie o "putere de solutionare" (eng.: "solving power") unei statistici date S.Pentru fiecare valoare a lui S va exista o echivocitate conditionata a cheii:

Echivocitate, cand S are valoarea sa particulara, iar aceasta este tot ce se stie despre cheie. Insemnatatea cantitativa a acestor valori:

da echivocitatea semnificativa a cheii cand S este cunoscut, P(S) fiind probabilitatea a priori a unei valori particulare S. Dimensiunea cheii H(K), mai putin aceasta echivocitate semnificativa, masoara "puterea de solutionare" a statisticii S.

Intr-un cifru ideal puternic, toate statisticile criptogramei sunt independente de cheia particulara utilizata. Aceasta este masura care protejeaza proprietatea:

pentru spatiul E sau

pentru spatiul M mentionat mai sus.

Exista statistici slabe sau bune, asa cum exista metode de trial si eroare slabe sau bune. Intr-adevar, testarea de tip trial si eroare a unei ipoteze este un tip de statistica si ceea ce a fost spus mai devreme privind cele mai bune tipuri de trial-uri contin generalitati. O statistica buna pentru rezolvarea unui sistem trebuie sa aiba urmatoarele proprietati:

1. Trebuie sa fie usor de masurat.

2. Trebuie sa depinda mai mult de cheie decat de mesaj, daca acesta presupune rezolvarea pentru cheie. Variatia cu M nu trebuie sa mascheze (acopere) variatia sa cu K.

3. Valoarea statisticii care poate fi "rezolvata" in ciuda "ambiguitatii" produse de variatia in M, trebuie sa imparta spatiul cheii intr-un numar de subseturi de probabilitati comparabile, in care statistica specifica acel subspatiu in care se afla cheia corecta. Statistica ar trebui sa furnizeze o informatie considerabila despre cheie, nu doar o mica fractiune dintr-un bit.

4. Informatia data trebuie sa fie simpla si folositoare. Astfel, subseturile in care statistica localizeaza cheia trebuie sa fie simple in spatiul cheii.

Frecventa care se bazeaza pe substitutia simpla este un exemplu de statistica foarte buna.

Doua metode (altele decat alegerea sistemelor ideale) se propun pe sine pentru descurajarea analizei statistice. Acestea pot fi numite metode de difuzie si confuzie. In metoda difuziei, structura statistica a lui M care conduce la redundanta sa este "disipata" intr-o varietate mare de statistici - adica, intr-o structura statistica ce presupune combinatii lungi de litere in criptograma. Efectul aici este acela ca inamicul trebuie sa intercepteze o cantitate mare de material pentru a reduce aceasta structura, din moment ce structura este formata din blocuri de probabilitate individuala foarte mica. Mai mult, chiar daca inamicul detine suficient material, munca analitica necesara este mai mare din moment ce redundanta a fost difuzata intr-un numar mare de statistici individuale. Un exemplu de difuzie a statisticilor este operarea pe un mesaj M = m₁, m₂, m₃, cu operatie de insumare, astfel incat:

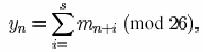
adaugand s litere succesive ale mesajului pentru a obtine litera y_n. Se poate arata ca redundanta secventei y este aceeasi cu cea a secventei m, dar structura a fost disipata. Astfel, frecventele literei in y vor fi mai apropiate decat in m, frecventele in diagrama deasemenea apropiate, etc. Intr-adevar, orice operatie reversibila care produce o litera in afara fiecarei litere si care nu are o memorie infinita, are o iesire cu aceeasi redundanta ca si intrarea. Statisticile nu pot fi nicicodata eliminate fara compresie, dar pot fi imprastiate (expandate).

Metoda confuziei este aceea de a face din relatia intre statisticile simple ale lui E si descrierea simpla a lui K o relatie complexa si de interes. In cazul substitutiei simple, este usor de descris limitarea lui K impusa de frecventele literei din E. Daca legatura este de interes si foarte confuza, inamicul poate fi capabil sa evalueze statistica S₁, sa spunem, care limiteaza cheia la o parte din spatiul cheii. Aceasta limitare, oricum, este pentru o regiune complexa R in spatiul, poate "folded ever" (intalnita) de multe ori, iar inamicului ii este dificil, din punct de vedere al timpului, sa o foloseasca. O statistica secundara S₂ limiteaza pe K aproape de R₂, pana cand el ajunge in regiunea de intersectie; dar aceasta nu ajuta prea mult, deoarece este dificil sa determini exact care este intersectia.   

Pentru a fi mai precis, sa presupunem ca spatiul cheii are cu siguranta "coordonate naturale" k₁, k₂, ., k_p pe care el (inamicul) vrea sa le determine. El masoara, sa spunem, un set de ststistici s1, s2, , sn si acestea sunt suficiente sa-l determine pe k_i .Oricum, in metoda confuziei, ecuatiile care contin aceste seturi de variabile sunt de interse si complexe. Avem, sa spunem:

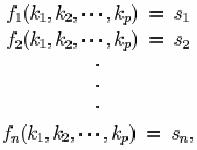
si toate f_i implica toate k_i.

Criptanalistul trebuie sa rezolve acest sistem simultan - o treaba dificila. In cazurile simple (nu cele confuze) functiile presupun doar un numar mic de k_i - sau macar o parte dintre acestia. Prima functie rezolva ecuatiile simple, evaluand cateva dintre k_i si substituindu-le pe acestea in ecuatii mai complicate.

Confuzia, aici, este urmatoarea: pentru sistemele de cifrare bune pasii trebuie facuti fie pentru difuzia sau confuzia redundantei (sau ambele).

24. METODA CUVANTULUI PROBABIL

Una din cele mai potrivite unelte pentru spargerea cifrurilor este folosirea cuvintelor probabile. Cuvintele probabile pot fi cuvinte sau fraze la care ne-am putea astepta in acel mesaj, din cauza sursei sale, sau pot fi pur si simplu cuvinte comune sau silabe care apar in orice text in acea limba, cum sunt the, and, tion, that si altele asemenea in engleza.

In general, metoda cuvintelor probabile este folosita astfel: presupunand ca un cuvant probabil se gaseste intr-un anumit punct in clar, cheia sau o parte din cheie este determinata. Aceasta este folosita pentru a descifra alte parti ale criptogramei si pentru a oferi un test de consistenta. Daca celelalte parti apar in clar, presupunerea este justificata.

Cateva din cifrurile de tip clasic folosesc o cheie de dimensiune mica si pot rezista mult timp la o analiza cu cuvinte probabile. Dintr-o considerare a acestei metode, putem incadra un test de cifruri care poate fi denumit testul acid. El se aplica doar cifrurilor cu o cheie de dimensiune mica (mai mica de, sa spunem, 50 de cifre zecimale), aplicat limbajelor naturale, si care nu foloseste metoda ideala de obtinere a secretizarii. Testul acid este acesta: cat de dificil este de determinat cheia sau o parte din cheie, cunoscand un mic esantion din mesaj si criptograma corespunzatoare. Orice sistem in care acest lucru este usor nu poate fi foarte rezistent, deoarece criptanalistul poate intotdeauna folosi cuvintele probabile, combinate cu incercarea si eroarea, pana cand este obtinuta o solutie consistenta.

Conditiile asupra dimensiunii cheii fac ca volumul de incercari si erori sa fie mic, iar conditia despre sisteme ideale este necesara, din moment ce acestea dau automat verificari de consistenta. Existenta cuvintelor si frazelor probabile este implicata de presupunerea limbajelor naturale.

Sa observam ca necesitatea solutiei dificile in aceste conditii nu este, prin ea insasi, contradictorie cu cerintele ca cifrarea si descifrarea sa fie procese simple. Folosind notatia functionala, avem, pentru cifrare,

Iar pentru descifrare,

Ambele pot fi operatii simple pe argumentele lor, fara ca a treia ecuatie,

sa fie simpla.

Putem de asemenea arata ca in investigarea unui nou tip de sistem de cifrare una din cele mai bune metode de atac este de a lua in considerare cum poate fi determinata cheia daca este dat un volum suficient din M si E.

Principiul confuziei poate fi (si trebuie sa fie) folosit la crearea dificultatilor pentru criptanalist folosind tehnicile de cuvinte probabile. Fiind date (sau presupunand cunoscute) M=m₁, m₂, , m_s­­ si E=e₁, e₂, . , e_s criptanalistul poate stabili ecuatii pentru elemente diferite k₁, k₂, , k_r (de fapt, ecuatiile de cifrare).

Presupunem ca totul este cunoscut, in afara lui k_i. Fiecare din aceste ecuatii ar trebui sa fie complexe in k_i si sa implice multe din ele. Altfel, inamicul le poate rezolva pe cele simple si apoi pe cele mai complexe prin substitutie.

Din punct de vedere al cresterii confuziei, este de dorit sa facem ca f_i-urile sa implice cateva m_i, mai ales daca acestea nu sunt adiacente si deci mai putin corelate. Aceasta introduce caracteristica nedorita a propagarii erorii, totusi, pentru ca atunci fiecare e_i va afecta in general cateva m_i-uri in descifrare, iar o eroare se va imprastia catre toate acestea.

Tragem concluzia ca o mare parte din cheie ar trebui folosita intr-o maniera implicata in obtinerea oricarei litere din criptograma mesajului pentru a pastra caracteristica muncii ridicata. Mai mult, este de dorit o dependenta de cateva m_i-uri necorelate, daca o anumita propagare a erorii poate fi tolerata. Suntem condusi catre toate trei argumentele acestor sectiuni pentru a lua in considerare "transformarile de mixare".

25. TRANSFORMARILE DE MIXARE

O notiune care s-a dovedit valoroasa in cazul teoriei probabilitatii este conceptul de transformare de mixare. Presupunem ca avem o probabilitate sau spatiul masurabil

si o masura care sa pastreze transformarea F a spatiului in el insusi, adica, o masura prin care regiunea transformata FR este egala cu masura regiunii initiale R. Transformarea este numita de mixare daca pentru orice functie definita peste spatiu si orice regiune R, integrala functiei peste regiunea:

aproximeaza, cu:

integrala functiei peste intreg spatiul:

multiplicat prin volumul lui R. Aceasta inseamna ca orice regiune initiala R este mixata cu o densitate uniforma prin intreg spatiul, daca F este aplicat de un numar mare de ori. In general,

devine o regiune ce contine un numar mare de fasii subtiri imprastiate peste

.

Cu cat n creste, fasiile devin din ce in ce mai fine, iar densitatea lor mai constanta (persistenta, continua). In acest sens precis, o transformare de mixare poate apare doar intr-un spatiu cu un numar infinit de puncte, iar pentru un punct finit din spatiu transformarea trebuie sa fie periodica. Se poate gandi ca o transformare de mixare este una care distribuie orice regiune consistenta, ordonata, rezonabila din spatiu, intr-un mod omogen peste intreg spatiul. Daca prima regiune poate fi descrisa in termeni simpli, cea de-a doua necesita termeni cu un inalt nivel de complexitate.

In criptografie, ne putem gandi la toate mesajele posibile de lungime N drept spatiul:

iar mesajele de probabilitate mare drept regiunea R. Acest grup din urma are o structura statistica simpla. Daca este aplicata o transformare de mixare, mesajele de probabilitate mare vor fi imprastiate prin spatiu.

Transformarile de mixare bune sunt de cele mai multe ori formate prin produsele repetate a doua operatii simple ne-comutative. Hopf¹³ a aratat, de ex., ca aceasta masa densa (aluat, eng.:"pastry dough") poate fi mixata printr-o astfel de secventa de operatii. Aluatul este pentru inceput rulat intr-o portiune subtire, apoi intins, apoi rulat din nou, si iar intinsa, etc.

Intr-o transformare de mixare buna a spatiului, cu coordonatele naturale X₁, X₂ , X_s, punctul X_i este tinut de transformarea intr-un punct:

cu

iar functiile f_i sunt complicate si presupun toate variabilele intr-un sens "senzitiv". O mica variatie a unuia,

sa spunem, schimba toate

in mod considerabil.

Daca

trece prin gama sa de variatie posibila, punctul:

traseaza o cale in zig-zag prin spatiu.

Metodele variate de mixare aplicabile secventelor statistice ale tipului gasit in limbajele naturale pot fi impartite. Una care arata foarte bine este aceea in care o transpozitie preliminara este urmata de o secventa de substitutii alternative si operatii simple liniare, si adaugarea de litere adiacente mod 26, de exemplu. Astfel, putem avea:

unde T este o transpozitie, L este o operatie liniara si S este o substitutie.

26. CIFRURI DE TIPUL T _kFS_j

Presupunem ca F este o transformare de mixare buna care poate fi aplicata unei secvente de litere si T_k si S_j sunt oricare doua familii simple de transformari, doua cifruri simple, care pot fi aceleasi. Mai concret, ne putem gandi la ele ca la doua substitutii simple.

Se pare ca cifrul TFS va fi un sistem de secretizare foarte bun din punct de vedere al caracteristicii muncii sale. In primul rand, este clar ca, in cazul argumentelor noastre referitoare la metodele statistice, nu exista statistici simple care sa furnizeze informatii despre cheie - orice statistica semnificativa derivata din E trebuie sa fie relevanta si senzitiva - redundanta a fost atat difuza, cat si confuza prin transformarea F. Deasemenea cuvintele probabile devin un sistem complex de ecuatii (care includ toate partile cheii, atunci cand mixarea este buna) care trebuie rezolvate simultan.

Este interesant de notat ca daca cifrul T este omis, sistemul ramas este similar cu S si astfel, nu prea puternic. Inamicul poate sa aplice operatia inversa mixarii (eng.:"unmixes") pentru criptograma, prin aplicarea lui F^-1 si apoi sa rezolve. Daca S este omis, sistemul ramas este mai puternic ca T singur, cand mixarea este buna, dar incomparabila cu TFS.

Principiul de baza aici, al cifrurilor simple separate prin transformarea de mixare, poate fi, desigur, extinsa. De exemplu, se poate folosi:

cu doua mixari si trei cifrari simple. Poate fi deasemenea simplificat prin utilizarea acelorasi cifruri, si chiar a acelorasi chei, la fel cu aceleasi transformari de mixare. Aceasta poate simplifica mult mecanismul acestor sisteme.    

Transformarea de mixare care separa doua (sau mai multe) aparitii ale cheii se comporta ca o bariera pentru inamic - este usor de tinut peste aceasta bariera un element cunoscut, dar cu unul nestiut (cheia), nu merge atat de usor.

Prin inlocuirea a doua seturi de necunoscute, si anume, cheia pentru S si cheia pentru T, si separandu-le prin transformarea de mixare F, vom obtine alaturarea (eng.: "entangled") necunoscutelor intr-o maniera care face ca solutionarea sa fie foarte dificila.

Desi sistemele construite pe baza acestui principiu vor fi extrem de sigure, ele au un mare dezavantaj. Daca mixarea este buna, atunci propagarea erorilor este rea. Eroarea de transmisie a unei litere va afecta cateva litere la descifrare.

27. INCOMPATIBILITATEA CRITERIILOR PENTRU SISTEMELE BUNE

Criteriul cinci pentru sistemele de secretizare bune dat in sectiunea 5 pare sa aiba o incompatibilitate sigura cand este aplicata unui limbaj natural cu o structura statistica a sa complicata. Cu limbajele artificiale care au o structura statistica simpla, este posibil sa satisfaci toate cerintele simultan, prin mijloacele date de cifrurile ideale. In limbajele naturale, trebuie facut un compromis si evaluarile echilibrate una in defavoarea alteia, cu o vizualizare asupra aplicatiei particulare.

Daca se renunta la unul dintre cele cinci, celelalte patru pot satisface foarte bine, asa cum arata exemplul urmator:

1. Daca omitem prima cerinta (cantitatea de secretizare) oricare cifru simplu, cum ar fi substitutia simpla va satisface. In caz extrem, de omitere a acestei conditii complet, nu este cerut nici un fel de cifru si va fi trimis direct clarul!

2. Daca dimensiunea cheii nu este limitata, atunci poate fi folosit cifrul Vernam.

3. Daca nu este limitata complexitatea operatiilor, pot fi utilizate procese de cifrare de tipuri diferite, extrem de complicate.    

4. Daca se omite conditia de propagare a erorii, va fi foarte bun un sistem de tipul TFS, desi este destul de complicat.

5. Daca se permite un mesaj mare, extins, vor fi cu usurinta dezvoltate multe sisteme diferite, in care mesajul corect este mixat cu multe altele, incorecte (eng.:"misinformation"). Cheia determina care dintre aceste mesaje este corect.

Un foarte puternic argument pentru incompatibilitatea celor cinci conditii poate fi dat in cele ce urmeaza: de la conditia 5, trebuie folosite, in esenta, sistemele secretizate asa cum au fost studiate in acest document. Sistemele perfecte si ideale sunt excluse prin conditiile 2, 3 si 4. Secretizarea ridicata ceruta de 1 trebuie sa provina dintr-o caracteristica a muncii inalta si nu dintr-o caracteristica de echivocitate inalta. Daca respectiva cheie este mica, sistemul simplu si erorile nu se propaga, probabil metodele pe cuvant vor rezolva in general usor sistemul, deoarece vom avea un sistem simplu de ecuatii pentru cheie.

Acest motiv este prea vag pentru a fi concluziv, dar ideea generala pare sa fie rezonabila. Poate daca diferitelor criterii le pot fi date semnificatii cantitative, pot fi gasite unele tipuri de ecuatii de schimbare care sa dea cele mai bune seturi de valori compatibile fizic. Doua dintre cele mai dificile de masurat numeric sunt: complexitatea operatiilor si complexitatea structurii statistice a limbajului.

ANEXA

Demonstrarea Teoremei 3

Se selecteaza orice mesaj M₁ si sunt grupate impreuna toate criptogramele care pot fi obtinute din M₁ prin orice operatie de cifrare T_i. Fie aceasta calsa de criptograme C₁. Grupam cu M₁ toate mesajele care pot fi obtinute din M₁ prin:

si le vom numi clasa C_1.

La fel va fi obtinut:

Daca vom incepe cu orice alt M in C₁, cat timp:

In mod similar, poate fi obtinut si C_1.

Alegand un M in C₁ (daca acesta exista) vom construi C₂ si

in acelasi mod. Continuand in acelasi mod, vom obtine clasa reziduala cu proprietatile (1) si (2). Fie M₁ si M₂ in C₁ si presupunem:

Daca E₁ este in:

si poate fi obtinut din M₁ prin:

atunci:

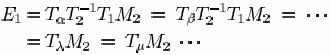
Astfel, fiecare M_i din C₁ va fi transformat in E₁ folosind acelasi numar de chei. In mod similar, fiecare E_i din C₁ este obtinut din orice M din C₁ folosind acelasi numar de chei. Ca urmare, acest numar de chei este un divizor al numarului total de chei si vom avea in continuare proprietatile (3) si (4).