Verificarea confirmarii ipotezelor privind datele, factorii si modelul

VERIFICAREA CONFIRMARII IPOTEZELOR PRIVIND DATELE, FACTORII SI MODELUL

"Cata exactitate au datele - care nu pot

fi decat probabile, cum spundea Laplace -

atat au si rezultatele" (O. Onicescu)

1. Ipoteze privind modelul si metoda de estimare

Incorsetarea unui proces economic in "chingile" unei ecuatii implica acceptarea unor ipoteze, aspect general valabil in oricare demers stiintific.

Acceptarea dependentei liniare, acceptarea unor factori pe considerentul ca exercita un rol determinant pentru procesul analizat reprezinta, in ultima instanta, prezumtii pe care ne bazam calculele. Prezumtiile pot fi, in continuare, detaliate tinand seama de cerintele metodei de estimare. Ele se pot referi la aspecte care privesc "comportamentul actorilor": y, x, u. astfel, variabila y este considerata o combinatie liniara in raport cu factorii plus perturbatia (u):

, (1

variabilele factoriale sunt independente intre ele fiind excluse relatiile liniare de tip ca si posibilitatea de a include un factor ale carui niveluri reprezinta o combinatie liniara de niveluri ale altor factori din ecuatia respectiva. De asemenea, in ce priveste variabila reziduala (u) se presupune ca valorile nu depind de vreun factor din model si prezinta, pe segmente de valori , o imprastiere egala. Comportamentul variabilei reziduale este presupus, de asemenea, a fi aleatoriu ca manifestare, fiind un reziduu care nu include nimic sistematic decat faptul ca urmeaza o lege normala, de medie egala cu zero, fara a exista vreo relatie de dependenta intre valori obtinute in succesiune.

Aceleasi ipoteze redate intr-o forma ceva mai riguroasa si in orice caz mai completa, pot fi exprimate astfel:

1 - Datele sunt obtinute corect(fara erori sistematice de observare) si in numar suficient de mare (depasind, in orice caz, numarul de parametrii care urmeaza sa fie estimati) asa incat solutiile sa prezinte stabilitate;

2 - Variabila factoriala (x) este nestochastica si prezinta aceleasi valori in eventualitatea in care repetam sondajul (nivelurile fixe in sensul regasirii acelorasi valori in colectivitati diferite);

3 - Factorul (x) prezinta variabilitate in ce priveste nivelurile inregistrate in cadrul unui esantion de date (dispersia fiind un numar pozitiv finit), asa incatrolul factorului sa poata fi pus in evidenta;

4 - Modelul de regresie este liniar in raport cu parametrii .

5 - Modelul de regresie este corect specificat in sensul alegerii functiei potrivite (liniare sau neliniare) si includerii factorilor importanti asa incat gradul de determinare () sa fie suficient de mare;

6 - Variabila reziduala este de medie zero si urmeaza, fie si asimptotic, o repartitie normala.

; ~ (2

7 - Variabila reziduala prezinta o imprastiere (dispersie) egala pentru diferitele valori (homoscedastica).

(3

intrucat iar .

8 - Variabila reziduala nu este corelata cu variabila factoriala (x), asa incat covarianta dintre si este zero.

(4

Aceasta ipoteza este legata direct de posibilitatea separarii influentei pe care o exercita "x" si "u" asupra variabilei y.

9 - Variabila reziduala nu este autocorelata in sensul ca pentru oricare doua valori () perturbatiile aferente nu sunt corelate:

(6

In matricea variantelor (dispersiilor) - covariantelor variabilei reziduale elementele nediagonale sunt egale cu zero.

10 - Factorii inclusi in model (varianta multifactoriala) sunt independenti unii in raport cu ceilalti, nefiind corelati (sau, cel putin, nefiind perfect corelati) intre ei.

Motivele pentru care in econometrie se pune accentul pe verificarea modalitatii in care astfel de prezumtii sunt confirmate, ar putea fi exprimate de constatari precum:

Economia, prin manifestarile ei in timp sau in structura, nu tine seama de cerintele metodelor destinate descrierii comportamentului ei. Ca urmare, putem avea "surpriza" de a constata ca unii factori sunt corelati sau situatii in care evolutia factorilor conduce la comportamente bizare ale variabilei-efect, manifestate prin abatei de la normal tot mai mari etc. Contracararea unor astfel de situatii presupune utilizarea unor variante metodologice adecvate;

Verificarile cu privire la confirmarea ipotezelor pot oferi explicatii cu privire la motivele pentru care verificarea semnificatiei (testul t, testul F) nu a condus la rezultatele asteptate;

Cresterea increderii in modelul elaborat ne indeamna "sa-l punem la treaba" si, functie de ceea ce poate (rezultate concretizate in estimatii, valori reziduale), sa-l apreciem. Daca aprecierea este, in general, pozitiva vis-a-vis de asteptari (confirma din perspectiva semnificatiei si ipotezelor) putem trece la etapa utilizarii lui pentru analize, prognoze, simulari.

Marile obstacole de care se loveste cercetarea econometrica sunt reprezentate mai ales de neconfirmarea ipotezelor mentionate si ele pot fi redate succint astfel (Kane M.):

Multicoliniaritatea;

Autocorelarea (valorilor reziduale);

Lipsa datelor;

Timpul si banii cheltuiti;

Heteroscedasticitatea;

Unicitatea ecuatiei si neidentificarea;

Specificarea incompleta sau incorecta.

Initialele "obstacolelor" enumerate formeaza numele MALTHUS.

In cele ce urmeaza ne referim la metodele de verificare a celor mai importante dintre prezumtiile mentionate precum si la implicatiile si solutiile presupuse de neconfirmarea acestora.

2. Date suficiente, neafectate de erori sistematice

Prezumtia cu privire la calitatea datelor poate fi exprimata in mod explicit sau poate fi subinteleasa (motiv pentru care nu este strict necesara includerea ei intre ipotezele de baza ale modelului). Urmatoarele motive importante consideram ca "pledeaza" pentru abordarea problemei datelor:

Modalitatea de obtinere a datelor nu indeplineste conditiile unei observari riguroase (din perspectiva modelarii econometrice) similare celor de laborator. Inregistrarile numerice la care avem acces au fost realizate in diverse scopuri (evidente financiar-contabile, raportari statistice, anchete sociale etc.) si in diverse conjuncturi de situatii (metodologii modificate in decursul timpului, intarzieri in ce priveste consemnarea realizarilor, durate inegale de activitate economica, situatii exceptionale etc.);

Imposibilitatea obtinerii de date privind unele dintre variabilele modelului econometric sau absenta unor inregistrari pentru o parte dintre cazuri sau perioade;

Importanta datelor, atat din perspectiva numarului de cazuri cat si in ce priveste calitatea "masuratorilor", pentru acuratetea solutiilor. Este posibil ca existenta unor date eronate, fie si pentru un singur caz, sa modifice estimarile, sa schimbe rezultatul testelor de semnificatie si, in final, sa puna sub semnul intrebarii utilitatea modelului.

Importanta datelor este subliniata si de urmatoarele aprecieri:

"Exista trei modalitati de a nu spune adevarul: direct prin minciuna, indirect prin calomnie, cel mai grav prin statistica." (Disraeli)

"Priveste de doua ori pentru a vedea corect (de 4 ori afirma Deming in studiile sale privind calitatea productiei) dar numai o singura data pentru a constata frumusetea." (Amiel)

"Rationamentul sistematic este minunat, nu da gres niciodata, dar ajunge sa existe un defect in datele initiale, pe care le introduci, ca impecabila concluzie sa fie eronata". (Penco, Gh., Bursan A.)

Ca urmare, acceptarea fara o prealabila verificare a prezumtiei care confera datelor calitatea de a fi complete si corecte, in situatia in care acestea se obtin de catre altii, iar scopurile sunt altele decat analiza econometrica, implica o serie de riscuri. Verificarea o consideram necesara si ea implica aprecierea datelor numerice din mai multe puncte de vedere. Redam, in cele ce urmeaza, astfel de "filtre", mentionand si solutiile recomandate in vederea acceptarii respectivelor exprimari numerice:

Existenta de date care se refera intr-un mod indubitabil la variabila-efect, repsectiv la fiecare dintre factorii inclusi in model. In cazurile in care datele nu corespund acestui deziderat (nu exista sau nu pot fi procurate date suficiente pentru una din variabile), se recurge la variabila cea mai apropiata ca sens si mod de a evolua (variabila-reprezentant) in vederea evitarii unei zone neexplicate () prea mari;

Controlul cantitatii in sensul aprecierii daca numarul de cazuri pentru care avem date este suficient de mare iar pentru fiecare caz datele sunt complete (exista inregistrarea privind , respectiv );

Daca numarul de cazuri este mult mai mic decat (nivel apreciat, din practica obtinerii de estimatii stabile, ca satisfacator, la limita) urmeaza sa adaugam cazuri sau sa inlocuim datele anuale cu date trimestriale sau lunare. Daca pentru unele cazuri (perioade din seria cronologica, unitati din esantion) datele nu sunt complete sau prezinta suspiciuni, procedam la corectii, daca acestea pot fi facute, sau la excluderea cazurilor respective, daca aceasta nu conduce la un volum prea mic (n<15) de cazuri;

Verificarea omogenitatii sub aspectul unitatii de masura, definirii indicatorului si exprimarii in preturi constante (pentru exprimari valorice). O astfel de verificare se refera la fiecare variabila in parte, asa incat pe intreg intervalul sau pentru intreg esantionul variabila sa fie exprimata unitar, sa rezulte in urma aceluiasi mod de calcul (masurare, agregare, formula de obtinere), prin utilizarea preturilor unei perioade de baza.

La ce ne putem astepta daca neglijam verificarea ipotezei privind corectitudinea datelor? Raspunsurile ar putea fi, functie de genul de eroare, urmatoarele:

Daca renuntam la unele variabile din lipsa de date, aceasta va saraci analiza, ar putea mari gradul de nedeterminare sau distorsiona estimatiile;

Daca, fie si pentru o variabila, datel sunt exprimate intr-o forma neomogena sau prezinta erori sistematice, acestea afecteaza grav solutiile modelului (practic utilitatea sa este compromisa).

Urmatorul exemplu are in vedere 2 posibilitati de obtinere a datelor:

a)      optica longitudinala (temporala) in care datele se refera la 13 luni succesive (t-13, t-12, t-1) privind: Q (productia in sute buc.) si M (numarul de angajati) la intreprinderea A.

b)      optica transversala in care datele se refera la 9 unitati (firme) care formeaza un esantion.

Tabelul 1

Date care formeaza seria de timp pot fi afectate de erori privind indeosebi: influenta modificarii pretului in timp, conditii total diferite de realizare a procesului, schimbarea definitiei sau a relatiei de calcul in decursul timpului, existenta trendului in date.

In exemplul prezentat, datele nu sunt afectate de inflatie (exprimarea este in unitati naturale) si se presupune ca nu au intervenit schimbari majore privind calitatea produsului si conditiile de productie cu exceptia numarului de angajati. In schimb, a aparut initial o eroare privind ordinea de marime, intrucat in luna t-5 cifra corecta este 55 si nu 5 500 (cum era initial, intrucat s-a omis faptul ca productia reprezinta sute bucati).

Datele obtinute in optica transversala pot fi afectate de erori ce privesc indeosebi numarul redus de cazuri in esantion, valori neschimbate pentru una dintre variabile, absenta inregistrarilor pentru unele unitati, aparitia unor cazuri atipice in esantion.

In exemplul prezentat putem constata ca eronate aspectele: numarul relativ redus de cazuri (doar 9 intreprinderi), absenta numarului de angajati la firma E.

Daca datele culese sunt destinate unui studiu avand drept obiectiv important prognoza, preferam utilizarea seriei de timp (a); daca obiectivul este destinat analizei rolului numarului de angajati asupra cresterii productiei, este mai indicata seria transversala (b) mai ales daca marim esantionul, eventual ne asiguram de reprezentativitatea lui in ansamblul firmelor de acelasi profil.

3. Variabilele factoriale din ecuatia de regresie sunt independente intre ele

Prezumtia independentei factorilor trebuie inteleasa intr-un sens mai nuantat, intrucat analogii si influente directe sau indirecte se constata peste tot in economie. In fig. 1 este sugerat un fel de "efect de domino", urmare a modificarii semnificative fie si a unei singure variabile, pentru ca declansarea unor modificari in lant sa se transmita asupra multor altor variabile. Din perspectiva estimarii parametrilor modelului, important este ca astfel de influente contaminate sa nu se manifeste sub forma unor corelatii foarte intense.

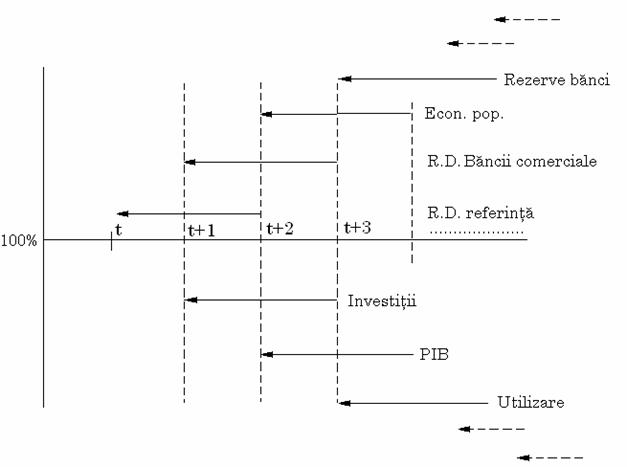
A)     Stare de stabilitate

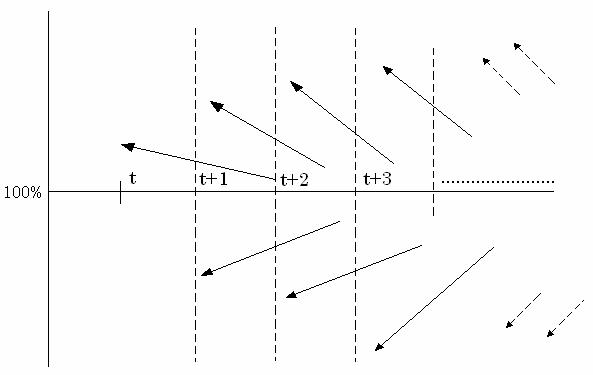
B)     Instabilitate urmare a modificarii variabilei "R.D. referinta"

Fig. 1

Daca intre variabilele factoriale ale modelului exista asemanari frecvente in ce priveste evolutia in timp sau in ce priveste modificarile de la o unitate de observare (familie, judet, firma) la alta, se considera ca ipoteza cu privire la independenta variabilelor cauzale incluse in modelul de regresie este infirmata. Termenul de multicoliniaritate se refera la astfel de situatii si el acopera atat cazul existentei in model a unui numar de 2 factori coliniari (perfect sau partial coliniari) cat si la cazul existentei de legaturi intense intre 3 sau mai multe variabile factoriale din ecuatia respectiva. Astfel de legaturi intre variabilele explicative incluse in reprezentari de forma pot fi expresii ale unei relatii de cauzalitate (x determinari pe z sau atat x cat si z depinde intens de factorul w neinclus in model), pot reprezenta combinatii liniare de forma , sau pot fi simple analogii in evolutia inregistrata pe segmentul de "n" valori de care dispunem. Toate aceste situatii produc aceleasi efecte daca asemanarile sunt foarte intense:

Estimatiile obtinute pentru parametri pot fi deformate;

Imprecizia acestora creste;

Rezultatele testului t indeosebi, sunt distorsionate in directia nesemnificatiei.

Pentru a avea o imagine mai concreta a implicatiilor nedorite pe care le poate genera multicoliniaritatea sa consideram urmatorul exemplu:

Pentru esantionul de 8 piete au fost culese date cu privire la: vanzari (y), oferta (x), pret (z).

Tabelul 2

Este acceptata urmatoarea functie a cererii:

In urma aplicarii analizei de regresie rezultatele au fost:

Rezultatele nu satisfac din perspectiva indicatorilor si nici in ce priveste semnul pozitiv al parametrului care se refera la rolul pretului (0,1989).

Se considera ca o posibila cauza ar putea fi coliniaritatea exprimarilor numerice care privesc variabilele x si z. se verifica prezumtia si, intr-adevar, coeficientul de corelatie dintre factori este foarte apropiat in valoare absoluta de 1 (). Analogia modificarilor pentru esantionul relativ mic (n=8) dar si efectele legii cererii si ofertei ar putea fi explicatii pentru o astfel de situatie. Ca urmare, se recurge la redimensionare, adaugandu-se inca 7 cazuri asa incat numarul de unitati sa ajunga la n

A rezultat ca prin simpla adaugare de cazuri pot fi obtinute ameliorari atat in ce priveste semnalarea sensului influentei factorilor (estimatia privind rolul pretului) cat si imprastierea S.e., determinatia ( a crescut), si testul F (semnificatie). Ceea ce a ramas de verificat este nesemnificatia parametrului -0,048.

In cele ce urmeaza, ne vom referi la semnalele care atrag atentia aspura prezentei multicoliniaritatii cu o intensitate mult prea mare precum si la posibilitatile de a "readuce lucrurile pe fagasul normal" in sensul diminuarii efectelor nedorite.

Semnale cu privire la multicoliniaritate:

a)      in cazul in care utilizam un model in care apar 2 factori ():

coeficientul de corelatie calculat pentru factori () intrece, in valoare absoluta, nivelul de 0,85 sau chiar de 0,9;

reprezentarea grafica (diagrama imprastierii), privind exclusiv factorii, semnaleaza o suspecta ordonare a punctelor de coordonate in jurul unei drepte;

b)      in cazul mai general in care apar 2 sau mai multi factori:

coeficientul de determinatie () fie prezinta valori apropiate de nivelul maxim (1 respectiv 100 ) in conditiile in care estimatiile pentru parametrii (una sau mai multe) nu trec testul t (n udifera semnificativ de zero);

coeficientul de determinatie (forma ajustata) este inferior ca marime coeficientilor de determinatie entru regresiile auxiliare.

Un semnal este dat si de determinantul matricei inverse , din relatia de estimare in sensul ca nivelul determinantului devine extrem de mic pe masura ce gradul de coliniaritate intre 2 factori creste (pentru coliniaritatea perfecta, determinantul devine zero, ceea ce face imposibila aplicarea relatiei (3.29). de aici decurge si o alta implicatie: un nivel mic al determinantului conduce la valori foarte mari ale elementelor inversei si, implicit, la elemente (vezi rel. 4.6b) ceea ce face ca imprastierea fiecarei valori estimate () sa prezinte valori mari. Intrucat o imprastiere mare este echivalenta cu o imprecizie mare, calitatea estimatorului de a fi eficient este afectata. La aceasta se adauga si faptul ca testul t include la numitor indicatorul imprastierii ( - vezi 4.1) care, amplificat fiind, conduce, frecvent, la nesemnificatie in ce priveste estimatia .

Solutiile pe care le putem avea in vedere in astfel de situatii sunt mai multe, fiecare cu avantajele si dezavantajele ei. Fiecare solutie implica un "daca", astfel:

daca putem suplimenta datele, marind astfel numarul de cazuri in esantion sau numarul de perioade in seriile cronologice, acestea actioneaza in directia cresterii marimii determinantului necesar calcularii inversei in relatia (3.29) mai ales daca intamplatoarele analogii in evolutia factorilor se atenueaza;

daca in loc de date culese in timp (serii cronologice) putem utiliza date obtinute in optica transversala (serii teritoriale, date privind bugetele de familie etc.), atunci acestea din urma ne asteptam sa fie mai putin afectate de corelatii intre factori si, ca urmare, solutia care este recomandata consta in utilizarea datelor daca acest din urma tip prezinta interes;

daca putem renunta la unul dintre factorii care prezinta o intensa corelatie cu un alt factor (sau este "prins" intr-o relatie de tip combinatie linirara), atunci eiminarea acestui factor ar fi o solutie. Conditia este ca eliminarea factorului sa nu afecteze analiza printr-o poerdere de informatie si nici gradul de determinare () in mod semnificativ;

daca nu urmarim in mod expres interpretarea parametrilor ci ne intereseaza doar atenuarea efectelor multicoliniaritatii (si cu deosebire diminuarea imprastierii si impreciziei estimatorului), atunci asa-numita regresie ridge poate fi o solutie. Procedeul consta in adaugarea unui scalar elementelor de pe diagonala inversei si estimarea in urma unei astfel de modificari.

Asadar,

(9

In exemplul considerat s-a avut in vedere prima dintre solutiile mentionate si intr-adevar suplimentarea cazurilor a condus la rezultate notabile in sensul micsorarii impreciziei estimatiilor (cu exceptia unui parametru) cresterii gradului de determinare, confirmarii modelului in sensul testului F.

Multicoliniaritatea reprezinta un "pericol" potential care trebuie avut in vedere in oricare cercetare aplicativa ("eine ewige Aufgabe") reprezentand totodata o problema deschisa pentru teoria econometrica.

4. Ipoteza privind liniaritatea modelului si corecta sa specificare

Liniaritatea relatiei de deendenta dintr variabila-efect (y) si factorul determinant (x), respectiv combinatia de modificari simultane a factorilor prezinta interes indeosebi din perspectiva utilizarii metodei celor mai mici patrate in vederea estimarii.

Deseori prin model liniar avem in vedere varianta transformata a modelului neliniar in raport cu variabilele. Aratam ca prin utilizarea logaritmilor sau a altor procedee, liniarizarea devine posibila (vezi par. 3.2, relatiile 3.35 - 3.37).

Verificarea prezumtiei liniaritatii poate fi realizata:

pe cale grafica, in sensul ca diagrama imprastierii este deseori elocventa mai ales in cazul unifactorial. In cazul multifactorial (cu deosebire cazul bifactorial) se poate analiza daca valorile y, respectiv x ce revin pe nuitate de factor "partener" (z) urmeaza forma liniara (similar );

in urma constatarii nivelului aproximativ constant al raportului modificarilor paralele de genul .

Deseori elaborarea modelului in mai multe variante face posibila analiza comparativa din perspectiva coeficientelor testul t, testul F. rezultatele analizei pot confirma sau infirma liniaritatea modelului in situatii in care exista cel putin 2 variante (una liniara, alta neliniara).

In ce priveste factorii luati in calcul, acestia trebuie sa indeplineasca conditii precum: influenta fiecaruia sa fie determinata pentru variabila-efect; factorii sa nu prezinte analogii intense in evolutie (multicoliniaritatea trebuie evitata), sa prezinte variabilitate.

Verificarea incorectei specificari din perspectiva factorilor atrasi in model are in vedere:

coeficienul de determinatie;

semnificatie in sensul testului t, dar si a testului F.

Un model econometric confirma asteptarile in ce priveste functia liniara adoptata daca gradul de determinare () este apropiat de 1 (100 ), testele de semnificatie (F,t) confirma modelul, abaterile reziduale se comporta precum valorile unei variabile aleatoare. Dar la caracteristicile erorii (u) urmeaza sa ne referim in capitolul urmator.