 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
I. Siruri
Def.1. Se numeste sir de numere reale orice functie ![]() , unde A este o submultime finita a lui N.
, unde A este o submultime finita a lui N.
Def.2. Un sir ![]() este marginit
este marginit ![]() .
.
-Un sir care nu este marginit se numeste sir nemarginit.
Def.3. Un sir ![]() este strict crescator
(crescator)
este strict crescator
(crescator) ![]()
Un sir ![]() este strict
descrescator (descrescator)
este strict
descrescator (descrescator) ![]()
Def.4. O multime V se numeste vecinatate a lui ![]() daca exista
daca exista ![]() .
.
Def.5. Un numar real x este limita unui sir ![]() daca orice vecinatate
a lui x contine toti termenii sirului, exceptand un numar finit de tremeni ai sai.
daca orice vecinatate
a lui x contine toti termenii sirului, exceptand un numar finit de tremeni ai sai.
Def.6. ![]()
-Produsul dintre un sir marginit si un sir convergent la zero este un sir convergent la zero.
![]() . Fie
. Fie ![]() ,
,![]() ,
,![]() trei siruri ce satisfac conditiile:
trei siruri ce satisfac conditiile:
1)
![]()
2)
![]()
Atunci ![]() are aceeasi limita a.
are aceeasi limita a.
![]() . Orice sir monoton si
marginit este convergent.
. Orice sir monoton si
marginit este convergent.
Dreapta incheiata.
![]()
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ;
;
6) 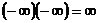 ; 7)
; 7) ![]() ; 8)
; 8) ![]() ; 9)
; 9)![]() .
. ![]()
Operatii
fara sens: 1) ![]() ; 2)
; 2) ![]() 3)
3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() .
.
![]() . a) Orice sir crescator si nemarginit are limita
. a) Orice sir crescator si nemarginit are limita ![]() .
.
b) Orice sir descrescator si
nemarginit are limita ![]() .
.
-a) ![]()
-b) ![]()
-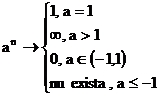
-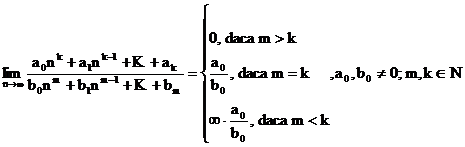
-Daca 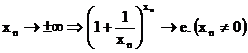
-Daca ![]()
-Daca ![]()
![]() . Fie
. Fie ![]() ,
,![]() cu proprietatile:
cu proprietatile:
1) ![]()
2) ![]()
3) ![]() este nemarginit
este nemarginit
4) ![]()
Atunci ![]()
-![]()
-Daca ![]() este definit prin
relatia
este definit prin
relatia ![]() cu
cu ![]() date, ecuatia
date, ecuatia ![]() se numeste ecuatia
caracteristica asociata relatiei de recurenta date.
se numeste ecuatia
caracteristica asociata relatiei de recurenta date.
a)Daca ![]()
b)Daca
![]() , c si d se determina din conditiile initiale.
, c si d se determina din conditiile initiale.
II. Limite de functii
![]() . Fie
. Fie ![]() s. n. Punct de
acumulare al multimii A daca
s. n. Punct de
acumulare al multimii A daca ![]() .
.
![]() .
. ![]() este limita functiei
este limita functiei ![]() in punctul de acumulare a al multimii E, daca
in punctul de acumulare a al multimii E, daca ![]() ,
,
![]() .
.
-Pentru a
arata ca o functie f nu are limita intr-un punct a, este suficient sa alegem
doua siruri ![]() si
si ![]() ,
, ![]() pentru care
pentru care ![]() au limite diferite.
au limite diferite.
![]() .
. ![]() este limita la stanga a functiei
este limita la stanga a functiei ![]() in punctul a -punct de
acumulare pentru
in punctul a -punct de
acumulare pentru ![]() , daca
, daca ![]() .
.
![]() .
. ![]() este limita la dreapta a functiei
este limita la dreapta a functiei ![]() in punctul a -punct de
acumulare pentru
in punctul a -punct de
acumulare pentru ![]() , daca
, daca ![]() .
.
![]() : Fie
: Fie ![]() ,
, ![]() -punct de acumulare
pentru E cu proprietatea ca f are limite laterale in a. Atunci urmatoarele
afirmatii sunt echivalente:
-punct de acumulare
pentru E cu proprietatea ca f are limite laterale in a. Atunci urmatoarele
afirmatii sunt echivalente:
f are limita in a
![]()
In aceste conditii ![]()
-![]()
- 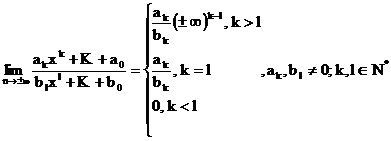
- Daca ![]() .
.
- Daca ![]() .
.
- Daca ![]() .
.
- Daca ![]() .
.
- 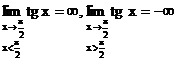
- ![]()
- ![]()
- ![]()
![]() . Fie
. Fie ![]() -punct de acumulare pentru E si
-punct de acumulare pentru E si ![]() . Daca:
. Daca:
1) ![]()
2) ![]() , atunci g are limita in a si
, atunci g are limita in a si ![]() .
.
-Limita produsului dintre o functie marginita si o functie de limita zero este zero.
![]() . Daca
. Daca ![]() -punct de acumulare pentru E,
-punct de acumulare pentru E, ![]() , atunci
, atunci ![]() .
.
-![]()
-![]()
-![]()
-![]() .
.
III. Functii continue
![]() Fie
Fie ![]() si
si ![]() punct de acumulare
pentru E. Spunem ca functia f este continua in a daca
punct de acumulare
pentru E. Spunem ca functia f este continua in a daca ![]() .
.
![]()
![]() este continua in a
este continua in a![]() .
.
![]() O functie
O functie ![]() este continua pe
este continua pe ![]() daca este continua in
orice punct din I
daca este continua in
orice punct din I
![]() Functiile elementare sunt continue.
Functiile elementare sunt continue.
![]() a)
a) ![]() este continua la dreapta in
este continua la dreapta in![]()
b) ![]() este continua la
stanga in
este continua la
stanga in![]()
![]()
![]() este continua in
este continua in ![]()
![]() f este continua la stanga si la dreapta in a.
f este continua la stanga si la dreapta in a.
![]() Fie
Fie ![]() punct de acumulare pentru E.
punct de acumulare pentru E.
Daca ![]() si g este continua in b, atunci
si g este continua in b, atunci ![]() .
.
![]() Fie E un interval.
Fie E un interval.
![]() are proprietatea lui
Darboux pe intervalul E, daca pentru orice puncte
are proprietatea lui
Darboux pe intervalul E, daca pentru orice puncte ![]() din E si orice numar
real
din E si orice numar
real ![]() situat intre
situat intre ![]() , exista
, exista ![]() .
.
![]() Orice functie continua
Orice functie continua ![]() , are proprietatea lui Darboux pe
, are proprietatea lui Darboux pe ![]() .
.
-Daca ![]() este continua si
este continua si ![]() este interval, atunci
este interval, atunci ![]() este interval.
este interval.
![]() Fie
Fie ![]() continua. Atunci f este marginita si isi atinge marginile pe
acest interval.
continua. Atunci f este marginita si isi atinge marginile pe
acest interval.
-Fie ![]() continua a.i.
continua a.i. ![]() . Atunci exista
. Atunci exista ![]()
![]() O functie
O functie ![]() este discontinua in
este discontinua in ![]() daca nu este continua in acest punct.
daca nu este continua in acest punct.
![]() Un punct
Un punct ![]() se numeste punct de discontinuitate de prima speta daca
exista
se numeste punct de discontinuitate de prima speta daca
exista ![]() dar nu are loc
egalitatea
dar nu are loc
egalitatea![]() .
.
![]() Un punct
Un punct ![]() se numeste punct de discontinuitate de speta a doua, daca nu
este punct de discontinuitate de prima speta a lui f.
se numeste punct de discontinuitate de speta a doua, daca nu
este punct de discontinuitate de prima speta a lui f.
IV Functii derivabile
![]() Se spune ca functia
Se spune ca functia ![]() are derivata in
are derivata in ![]() daca limita
daca limita ![]() .
.
Daca ![]() , f se numeste derivabila in
, f se numeste derivabila in ![]() .
.
![]() a)
a) ![]() are derivata la stanga in
are derivata la stanga in ![]() pentru care
pentru care ![]() daca
daca 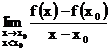 exista in
exista in ![]() .
. ![]()
b) ![]() are derivata la dreapta in
are derivata la dreapta in ![]() pentru care
pentru care 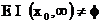 daca
daca 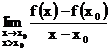 exista in
exista in ![]() .
. ![]()
![]() Functia f are
derivata in
Functia f are
derivata in ![]() f are derivate laterale in
f are derivate laterale in ![]() si
si ![]() .
.
![]() Fie
Fie ![]() , f continua in
, f continua in ![]() . Daca f are derivata in
. Daca f are derivata in ![]() si daca graficul este
convex (concav) de o parte a lui
si daca graficul este
convex (concav) de o parte a lui ![]() si convex (concav) de
cealalta parte,
si convex (concav) de
cealalta parte, ![]() se numeste punct de
infelxiune al functiei f.
se numeste punct de
infelxiune al functiei f.
![]() Un punct
Un punct ![]() se numeste punct de
intoarcere pentru graficul functiei
se numeste punct de
intoarcere pentru graficul functiei ![]() , f continua in
, f continua in ![]() , daca derivatele laterale ale functiei f in
, daca derivatele laterale ale functiei f in ![]() sunt infinite si
diferite.
sunt infinite si
diferite.
![]() Un punct
Un punct ![]() se numeste punct
unghiular pentru graficul functiei
se numeste punct
unghiular pentru graficul functiei ![]() , f continua in
, f continua in ![]() , daca derivatele laterale ale functiei f in
, daca derivatele laterale ale functiei f in ![]() sunt diferite si cel
putin una este finita.
sunt diferite si cel
putin una este finita.
![]() Orice functie
derivabila intr-un punct este continua in acel punct.
Orice functie
derivabila intr-un punct este continua in acel punct.
![]()
![]() . f este derivabila pe intervalul
. f este derivabila pe intervalul ![]() , daca f este derivabila in orice punct al intervalului I.
, daca f este derivabila in orice punct al intervalului I.
-Derivatele functiilor elementare
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
7) ![]()
8) ![]()
9) ![]()
10) ![]()
11) ![]()
12) ![]()
13) ![]()
-Reguli de derivare
1) ![]()
2) ![]()
3) ![]()
4) 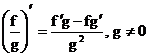
5) ![]()
6) ![]()
7) ![]()
![]() Un punct
Un punct ![]() se numeste punct de
maxim local al functiei
se numeste punct de
maxim local al functiei ![]() , daca exista o vecinatate V a lui a astfel incat
, daca exista o vecinatate V a lui a astfel incat ![]() .
.
![]() Un punct
Un punct ![]() se numeste punct de
minim local al functiei
se numeste punct de
minim local al functiei ![]() , daca exista o vecinatate V a lui b astfel incat
, daca exista o vecinatate V a lui b astfel incat ![]() .
.
![]() Un punct de minim
local sau de maxim local pentru o functie
Un punct de minim
local sau de maxim local pentru o functie ![]() se numeste punct de
extrem local al functiei. Valorile functiei in punctele de extrem se numesc
extremele functiei.
se numeste punct de
extrem local al functiei. Valorile functiei in punctele de extrem se numesc
extremele functiei.
![]() Fie
Fie ![]() , E-intreval iar
, E-intreval iar ![]() un punct de extrem din
interiorul intervalului. Daca f este derivabila in
un punct de extrem din
interiorul intervalului. Daca f este derivabila in ![]() , atunci
, atunci ![]() .
.
![]() Fie
Fie ![]() ,
, ![]() . Daca:
. Daca:
f este
continua pe ![]() ;
;
f este
derivabila pe ![]() ;
;
![]()
atunci exista ![]() astfel incat
astfel incat ![]() .
.
![]() Fie
Fie ![]() ,
, 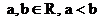 . Daca:
. Daca:
f este
continua pe ![]() ;
;
f este
derivabila pe ![]() ;
;
atunci exista ![]() astfel incat
astfel incat ![]() .
.
![]() Fie
Fie ![]() ,
, ![]() . Daca:
. Daca:
f,g
continue pe ![]() ;
;
f,g
derivabile pe ![]() ;
;
![]()
atunci ![]() si exista
si exista ![]() astfel incat
astfel incat ![]() .
.
-Fie ![]() , (E-interval) derivabila.
, (E-interval) derivabila.
Daca ![]() , atunci f este crescatoare (strict crescatoare) pe E
, atunci f este crescatoare (strict crescatoare) pe E
Daca ![]() , atunci f este descrescatoare (strict descrescatoare)
pe E.
, atunci f este descrescatoare (strict descrescatoare)
pe E.
-Fie ![]() , E-interval si
, E-interval si ![]() . Daca:
. Daca:
f este
continua in ![]()
f este
derivabila pe ![]()
Exista ![]() ,
,
atunci f are derivata in ![]() si
si ![]() . Daca
. Daca ![]() , atunci f este derivabila in
, atunci f este derivabila in ![]() si
si ![]() .
.
![]() Daca f este o functie derivabila pe un interval E,
atunci derivata f' are proprietatea lui Darboux pe E.
Daca f este o functie derivabila pe un interval E,
atunci derivata f' are proprietatea lui Darboux pe E.
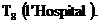 Fie
Fie ![]() . Daca:
. Daca:
f,g
derivabile pe ![]() ;
;
![]() ;
;
![]() ;
;
Exista ![]() ,
,
atunci exista ![]() .
.
 Fie
Fie ![]() . Daca:
. Daca:
f,g derivabile pe ![]() ;
;
![]() ;
;
![]() ;
;
Exista ![]() ,
,
atunci exista ![]() .
.
![]() Fie
Fie ![]() , E-interval.
, E-interval.
f se
numeste convexa pe E ![]()
f se
numeste concava pe E ![]()
![]() Fie
Fie ![]() o functie de doua ori
derivabila pe
o functie de doua ori
derivabila pe ![]() .
.
Daca ![]() , atunci f este convexa pe
, atunci f este convexa pe ![]() .
.
Daca ![]() , atunci f este concava pe
, atunci f este concava pe ![]() .
.
![]() Fie
Fie ![]() , E-interval si
, E-interval si ![]() . Daca f este de doua ori derivabila intr-o vecinatate
V a lui
. Daca f este de doua ori derivabila intr-o vecinatate
V a lui ![]() si daca exista doua
numere
si daca exista doua
numere ![]() astfel incat:
astfel incat:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() , atunci
, atunci ![]() este punct de
inflexiune pentru f.
este punct de
inflexiune pentru f.
![]() Fie
Fie ![]() ,
, ![]() punct de acumulare pentu E.
punct de acumulare pentu E.
1) Dreapta ![]() se numeste asimptota
verticala la stanga a functiei f, daca
se numeste asimptota
verticala la stanga a functiei f, daca ![]()
2) Dreapta ![]() se numeste asimptota
verticala la dreapta a functiei f, daca
se numeste asimptota
verticala la dreapta a functiei f, daca ![]()
![]() 1) Fie
1) Fie ![]() a.i.
a.i. ![]() Dreapta
Dreapta ![]() se numeste asimptota oblica la ramura spre
se numeste asimptota oblica la ramura spre ![]() a functiei f,
daca
a functiei f,
daca ![]() .
.
2) Fie ![]() a.i.
a.i. ![]() Dreapta
Dreapta ![]() se numeste asimptota oblica la ramura spre
se numeste asimptota oblica la ramura spre ![]() a functiei f,
daca
a functiei f,
daca ![]() .
.
![]() 1)
1) ![]() este asimptota oblica
la ramura spre
este asimptota oblica
la ramura spre ![]() a functiei f
a functiei f ![]() ,
, ![]()
2) ![]() este asimptota oblica
la ramura spre
este asimptota oblica
la ramura spre![]() a functiei f
a functiei f ![]()
![]() ,
, ![]()
3) Daca ![]() , dreapta
, dreapta ![]() se numeste asimptota
orizontala spre
se numeste asimptota
orizontala spre ![]() a functiei f.
a functiei f.
4) Daca ![]() , dreapta
, dreapta ![]() se numeste asimptota
orizontala spre
se numeste asimptota
orizontala spre ![]() a functiei f.
a functiei f.
Copyright © 2025 - Toate drepturile rezervate