Numere Complexe

Numere Complexe

Forma algebrica a unui numar complex

Prin produsul cartezian RXR intelegem multimea , pe aceasta multime definim operatiile algebrice de adunare si inmultire .

Fie Z₁=si Z₂= ; Z₁ ,Z₂ RXR

Adunarea Z₁+Z₂=RXR ,

caz particular : Z₁+Z₂=RXX R

Inmultirea Z₁ Z₂=RXR ,

caz particular : Z₁∙Z₂=RXX R

pentru cazul general avem :

DEF: Multimea numerelor RXR pe care am definit operatiile algebrice de adunare si de inmultire se numeste multimea numerelor complexe notata cu "C" ,

Notam cu multimea numerelor complexe nenule .

a = se numeste partea reala a lui "z" (se mai noteaza uneori a= R e ) ;

b = se numeste partea imaginara a lui "z" (se mai noteaza uneori a= I m ) .

Daca b = 0 , atunci Z = aR RC

Daca a = 0 , atunci Z = bi , b 0 se numeste numar complex pur imaginar

Forma algebrica a unui numar complex Z este Z= a + bi , i ² = -1

Operatii algebrice cu numere complexe :

Fie Z₁=si Z₂= ; Z₁ = a₁ + b₁ i ; Z₂ =a₂ +b₂ i ; Z₁ ,Z₂ RXR

Adunarea :

Z₁ + Z₂= a₁ + b₁ i + a₂ +b₂ i = a₁+a₂ + i(b₁ +b₂) =

Proprietati :

1) Asociativitatea (Z₁ +Z₂ )+Z₃ =Z₁ +( Z₂ +Z₃ ) ,

2) Comutativitatea Z₁ +Z₂= Z₂ +Z₁    ,

3) Elementul neutru ( 0 =0 + 0i ) , i asfel incat Z+0=0+Z=Z ,

4) Elemente opuse Z+(-Z)=(-Z) +Z = 0 ,

OBS :Spunem ca multimea "C" impreuna cu operatia de adunare si operatiile 1 , 2 , 3 , 4 formeaza

grupul aditiv comutativ al numerelor complexe .

Inmultirea :

Z₁ ∙ Z₂= (a₁ + b₁ i ) ∙ (a₂ +b₂ i ) = =

Proprietati :

1) Asociativitatea (Z₁ ∙Z₂ ) ∙ Z₃ =Z₁ ∙ ( Z₂ ∙ Z₃ ) ,

2) Comutativitatea Z₁ ∙ Z₂= Z₂ ∙ Z₁    ,

3) Elementul neutru ( 1 =1 + 0i ) , i asfel incat Z+1=1+Z=Z ,

4) Elemente inversabile Z∙Z^-1 = Z^-1 ∙Z= 1 ,

5) Distributivitatea in raport cu adunarea Z₁ ∙ (Z₂ +Z₃ ) =Z₁ ∙Z₂ + Z₁ ∙ Z₃

OBS :Spunem ca multimea "C" impreuna cu operatia de inmultire si operatiile 1 , 2 , 3 , 4 (si operatia de adunare cu operatiile 1 , 2 , 3 , 4 ) formeaza corp comutativ al numerelor complexe , numit corpul comutativ al numerelor complexe .

Multimea "C" nu este ordonata , adica un numar complex nu poate fi inferior sau superior altui

numar complex ( nu prezinta relatia de ordine < sau > )

Numere complexe conjugate

DEF : Fie Z = a + bi C .Se numeste conjugatul lui Z notat , numarul complex = a - bi

Proprietati

1) Suma a doua numere complexe conjugate este egala cu un numar real Z+R , .

2) Produsul a doua numere complexe conjugate este egal cu un numar real Z ∙ R , .

3) Conjugatul a sumei a doua numere complexe este egal cu suma conjugatelor celor doua numere

complexe , .

4) Conjugatul a produsului a doua numere complexe este egal cu produsul conjugatelor celor doua

numere complexe , .

5) Conjugatul a catului a doua numere complexe este egal cu catul conjugatelor celor doua numere

complexe , .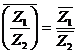

6) (OBS : ; ;

Modulul unui numar complex

DEF : Fie Z = a + bi C .Se numeste modulul numarului complex Z , notat, numarul pozitiv = .

Proprietati

1) ,

2) Modulul unui numar complex coincide cu modulul conjugatului sau, = , .

3) Produsul dintre un numar complex si conjugatul sau este egal cu patratul modulului acelui numar

∙ = , .

4) Modulul produsului a doua numere complexe este egal cu produsul modulelor celor doua numere .

, .

5) Modulul catului a doua numere complexe este egal cu catul modulelor lor .

, .

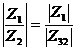6)Inegalitatea triunghiului (sau inegalitatea lui Minkowski )

Radacinile patrate ale unui numar complex

DEF : Fie ZC . Se numeste radacina patrata a lui "Z" un numar complex "r" C cu propietatea r² =Z .

Teorema : Orice numar complex nenul admite doua radacini patrate opuse .

EX: r ₁=1+i este radacina patrata a lui Z=2i r₁² = (1+i)² =2i =Z.

Rezolvarea ecuatiei de grad II cu coeficienti numere complexe

Teorema : Ecuatia : aX² +bX+c=0 ; a, b , c R , a, cu are doua radacini complexe conjugate date de formulele :