Calculul cu diferente finite

Calculul cu diferente finite

La determinarea polinoamelor de interpolare se utilizeaza calculul cu diferente finite aplicate asupra multimii de date

Fie functia y=f(x) tabelata in puncte echidistante si h - pasul retelei.

Definitie: Se numeste diferenta finita de ordinul 1, la dreapta, pentru f(x), expresia:

(17)

Conform definitiei, diferentele finite de ordin superior se exprima prin relatia:

(18)

Obs: Utilizarea discretizarii cu pas egal conduce la simplificarea calculelor prin scrierea valorilor variabilei independente sub forma: x₀, x₀+h, x₀+2h, ..x₀+nh sau x₀+ih

Proprietatile operatorului diferenta "

- aditivitatea

- omogenitatea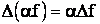

Se mai definesc urmatorii operatori:

- translatia: (19)

- diferenta simetrica:

- media:

Din relatiile 17 si 18, aplicand proprietatile operatorului diferenta (relatiile 19), rezulta:

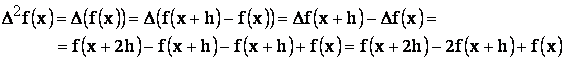
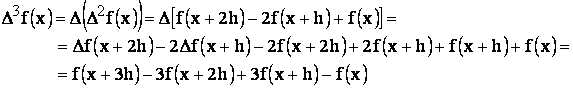
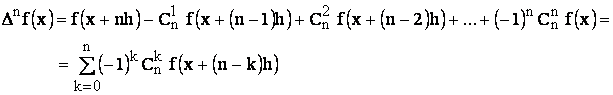(20)

Cu relatia 20 se poate construi tabelul diferentelor finite ale functiei f, necesar pentru obtinerea unor tipuri de polinoame de interpolare.

Presupunem ca se cunosc (n+1) puncte de pe graficul functiei y = f(x).

Rezulta ca avem:

(21)

Pentru aplicatii se construieste tabelul:

Calculul diferentelor finite generalizate ale lui x:

Definitie: Produsul se numeste puterea generalizata a lui x.

Obs. Pentru h = 0:

adica, puterea generalizata coincide cu puterea obisnuita.

Diferentele finite ale puterii generalizate ale lui x:

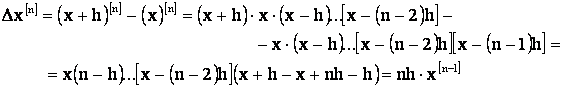(22)

Prin inductie completa:

Obs. Pentru k > n, rezulta: .