Metoda contururilor vectoriale

Metoda contururilor vectoriale

Aceasta metoda permite rezolvarea parametrilor cinematici pe cale analitica si se poate rezolva cu usurinta daca in procesul de rezolvare apar numai doua necunoscute. In cazul in care apar mai multe necunoscute, se scriu ecuatiile respective rezultand sisteme de n ecuatii cu n necunoscute care se rezolva prin metode obisnuite. Se mentioneaza ca la mecanismele complexe, sistemele de ecuatii pot avea grade mai mari si in unele situatii ecuatiile pot fi si neliniare. In aceste situatii rezolvarea se poate face numai prin metode aproximative cu ajutorul calculatorului.

Metoda contururilor vectoriale se aplica la mecanismele plane si consta in:

1. Se ataseaza mecanismului un sistem de axe fix.

2. Se imparte mecanismul in mai multe contururi poligonale inchise, intr-o anumita ordine. Numarul contururilor se poate stabili cu relatia:

(2.43)

in care; - numarul cuplelor de clasa 5, iar n'- numarul elementelor mobile.

3. Pentru fiecare contur poligonal se ataseaza vectorii care conduce la obtinera unei ecuatii de inchidere.

4. Rezolvind aceste ecuatii se determina parametrii cinematici ai mecanismului.

5. Sensul de masurare este trigonometric.

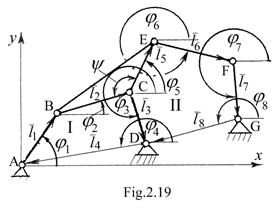
In Fig.2.19, se prezinta un mecanism cu doua contururi poligonale inchise si deformabile care au urmatoarele ecuatii de inchidere:

I (2.44)

II

Aceste contururi vectoriale sunt caracterizate de urmatorii parametri: I- variabila independenta ; parametrii constanti ; parametrii necunoscuti iar pentru II- parametrii constanti ; parametrii variabili necunoscuti . Intre parametrii celor doua contururi exista anumite legaturi: - comun;.

Daca se analizeaza cele doua contururi se constata ca conturul I are doua necunos- cute, iar conturul II trei necunoscute insa una dintre aceste necunoscute depinde de una din conturul I. In rezolvare pot fi trei obtiuni: elementul conducator putand fi elementul

Primele variante sunt favorabile introducand in contururi numai cate doua necunoscute, situatie usor de rezolvat. In varianta trei, apar trei necunoscute in poligonul II de langa elementul conducator si care nu poate fi rezolvat inependent. Rezolvarea se poate face numai pentru ambele poligoane simultan. Evident, caz mult mai greu de rezolvat. Din acest motiv s-a precizat in etapa 2 " anumita ordine".

Ca aplicatie, se considera un mecanism patrulater, Fig.2.20 cu urmatorii parametri:

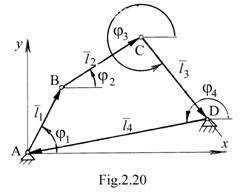
- variabila independenta care determina, in primul rand, viteza unghiulara si acceleratia unghiulara a elementului conducator care, apoi, se transmite la urmatorii parametri variabili; parametrii constanti- ; parametrii variabili - care derivati conduc la aflarea vitezelor si apoi a acceleratiilor ungiulare ale elementelor respective.

Prin analiza cinematica se pot urmari mai multi parametri cinematici din care cei mai importanti sunt: pozitia unghiulara a elementelor 2 si 3 fata de elementul fix 1; vitezele si acceleratiile unghiulare absolute ale elementelor; vitezele si accelratiile unghiulare relative dintre elemente; vitezele si acceleratiile absolute ale unor puncte de pe mecanism; traiectoriile unor puncte.

Rezolvarea pozitiilor unghiulare

Se scrie ecuatia vectoriala a contutului poligonal ABCD, parcurs in sens orar:

(2.45)

Se proiecteaza ecuatia (2.45) pe axele sistemului fix, rezultand sitemul de doua ecuatii scalare:

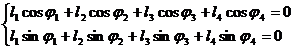(2.46)

Se fac notatile:

(2.47)

Se separa variabilele din sistemul (2.46) si se introduc notatiile (2.47) rezultand sistemul urmator:

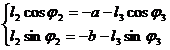(2.48)

Se ridica la patrat fiacare ecuatie a sistemului (2.48)si se aduna, membru cu membru,

rezultand:

(2.49)

Se imparte relatia (2.49) la 2al₃ , si se fac notatiile:

In aceste conditii, relatia (2.49) capata forma:

(2.50)

Solutiile ecuatiei (2.50) sunt:

(2.51)

in care; .

Dintre cele doua solutii se alege solutia pentru care are sens functia cosinus, adica Revenind la vechea variabila, se obtine necunoscuta:

(2.52)

Daca se noteaza , dintr-o ecuatie a sistemului (2.48) rezulta , de unde rezulta urmatoarea necunoscuta:

(2.53)

Vitezele unghiulare absolute

Se deriveaza ecuatiile scalare ale sistemului (2.46) si rezulta un nou sistem:

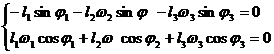(2.54)

unde; ; ; .

Pentru rezolvare, se apeleaza la un artifici simplu de a se roti sistemul de axe fix cu unghiul, apoi cu in sens pozitiv si se transccreie prima ecuatie a sistemului (2.54) in noile sisteme rezultand relatiile:

(2.56)

Considerand ca se obtin vitezele unghiulare:

Acceleratiile unghiulare absolute

Se deriveaza prima ecuatie a sitemului (2.54) rezultand ecuatia:

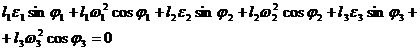(2.57)

Considerand si utilizand acelasi artificiu de rotire a sitemului fix si de transcriere a ecuatiei (2.57) in noile sisteme, rezulta relatiile (2.58) din care se deduc acceleratiile unghiulare absolute.

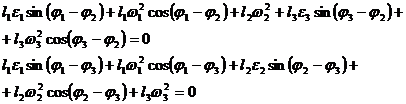(2.58)

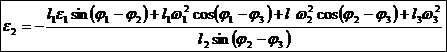
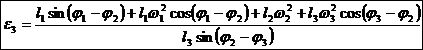
Vitezele si acceleratiile unghiulare relative

Miscarea relativa din cuplele de rotatie B si C se determina cu relatiile urmatoare:

viteze acceleratii

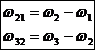
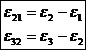
De precizeaza ca vitezele si acceleratiile absolute se introduc, in aceste relatii, cu semnele rezultate din calcul.

Vitezele si accelwratiile absolute ale unor puncte

Se folosesc ecuatiile analitice obtinute din transformarea ecuatiilor vectoriale.

Problema traiectoriilor

Pentru cuplele B si C, cat si pentru alte puncte de pe elementele 1 si 3, traiectoriile sunt cercuri de forma:

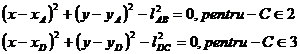(2.60)

Daca punctele apartin bielei BC, ecuatiile parametrice se scriu usor insa ecuatiile de forma se obtin mai greu folosind o metoda generala utilizata in mecanica teoretica, cunoscute sub denumirea de ecuatiile lui Roberts pentru curbe de biela care sunt ecuatii de gradul 6.