 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
Calcul integral
Functii primitivabile
Definitie, proprietati, tabel de primitive
Definitie: O functie f : I→ R (I![]() interval) se numeste primitivabila daca exista
interval) se numeste primitivabila daca exista
F : I→R
derivabila astfel incat ![]() F se numeste primitiva
a functiei f si vom nota cu
F se numeste primitiva
a functiei f si vom nota cu
![]() =F+c
=F+c
F- multimea tuturor primitivelor functiei f.
Observatie:
Avem ![]() =F+C, unde cu C am notat multimea functiilor constante
definite pe I cu valori reale.
=F+C, unde cu C am notat multimea functiilor constante
definite pe I cu valori reale.
Teorema: (Liniaritatea operatorului de primitivare)
Daca f,g: I →R sunt primitivabile si ![]() atunci f+g si
atunci f+g si ![]() sunt primitivabile si in plus:
sunt primitivabile si in plus:
![]()
![]()
Teorema: Daca f : I→ R este continua atunci f este primitivabila.
2.Daca f : I→ R este primitivabila atunci f are proprietatea lui Darboux.
Tabel de primitive:
1. 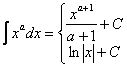
![]()
2. ![]()
In particular ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]()
![]()
10. ![]()
11. ![]()
12. ![]()
13. ![]()
Observatie: La scrierea acestor formule nu am precizat cine
este intervalul I![]() pe care sunt valabile. Astfel la formula (1) daca:
pe care sunt valabile. Astfel la formula (1) daca:
a > -1atunci I![]() ;
;
a ≤ 1 a ![]()
![]() atunci I
atunci I![]() *;
*;
a ≤ -1 a ![]() R -Z atunci I
R -Z atunci I![]() (0,
(0,![]() ).
).
Formulele (5)
si (7) sunt valabile pentru I![]()
![]()
Formulele (6)
si (8) au loc pentru I![]()
![]()
Formula (9)
este valabila pentru I![]()
![]()
Formula (11)
este valabila pentru I![]() ) sau I
) sau I![]()
![]() .
.
Formula (13)
este valabila pentru I![]() .
.
Formula de integrare prin parti
Teorema: Daca f,g:I →R sunt derivabile cu derivate continue atunci:
![]()
Observatie: Aceasta formula poate fi aplicata cu succes in mai multe situatii. Precizam doua dintre cele mai des intalnite.
I. ![]() este ex, sin x, cos x si g este ex,
sinx,cos x sau o functie polinomiala.
este ex, sin x, cos x si g este ex,
sinx,cos x sau o functie polinomiala.
Exemplu:
1) ![]() 2)
2) ![]()
Solutie:
1. ![]()
Atunci ![]() 2.
2. ![]()
g(x)=cos x ![]()
![]()
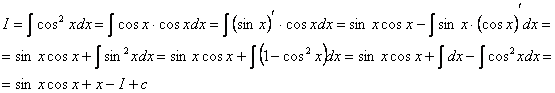
I=sin x cos x+x -I+c
![]()
II. ![]() este o functie polinomiala si g (x)=lnkx, k
este o functie polinomiala si g (x)=lnkx, k![]() N*
N*
Exemple:
1)
![]() 2)
2)
![]()
Solutie:
1. ![]()
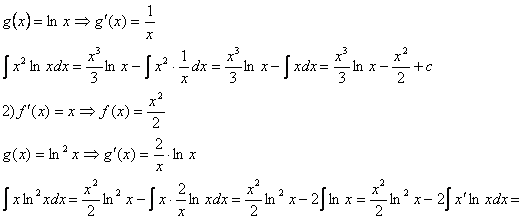
![]()
Formula schimbarii de variabila
Teorema: (Prima formula de schimbare de variabila)
Fie I,J![]() R intervale. Daca f:J →R este primitivabila si
R intervale. Daca f:J →R este primitivabila si ![]() este derivabila
atunci (f
este derivabila
atunci (f![]() admite pe I
primitiva F
admite pe I
primitiva F![]() , unde f este o
primitiva oarecare a functiei f, adica:
, unde f este o
primitiva oarecare a functiei f, adica:
![]()
Exemplu:
1. ![]() 2.
2. ![]()
Solutie:
Facem substitutia x2=t de unde 2xdx=dt
Atunci
![]()
2. Facem substitutia x2-1=t de unde 2xdx=dt
adica ![]()
![]() . Atunci:
. Atunci:
![]()
Teorema (Formula de schimbare de variabila)
Fie I, J![]() R intervale. Daca f
R intervale. Daca f![]() R admite primitive,
R admite primitive, ![]() este bijectiva, derivabila, cu derivata nenula pe I atunci f
admite pe I primitiva G
este bijectiva, derivabila, cu derivata nenula pe I atunci f
admite pe I primitiva G![]() unde G este o primitiva pentru (
unde G este o primitiva pentru (![]() iar
iar ![]() este inversa functiei
este inversa functiei ![]() . Deci:
. Deci:
![]()
Exemplu
![]()
Aceasta integrala poate fi rezolvata in doua moduri:
Cu ajutorul integrarii prin parti
Facand substitutia x=sht, unde sht![]() sinus hiperbolic deci dx=cht. Avem
sinus hiperbolic deci dx=cht. Avem
![]()
![]() (1)
(1)
Din x = sht![]() de unde t = ln(x+
de unde t = ln(x+![]() )
)
Si inlocuind in (1) obtinem
![]()
![]()
Calculul prin recurenta a unor integrale
Pentru exemplificare vom considera:
I![]()
![]() n
n![]() , a
, a![]()
Observam ca:
![]()
Dorim sa gasim o relatie de recurenta adica o formula care exprima In(x) in functie de In-1(x). Utilizand aceasta relatie de recurenta din I1(x) vom putea deduce valoarea lui I2(x), din I2(x) va rezulta I3(x) si asa mai departe.
Pentru n≥2 vom avea:
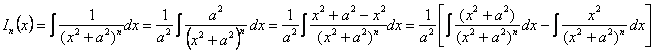
In(x)=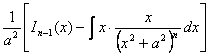
![]()
Vom face schimbarea de variabila x2+a2=t. Atunci 2xdx=dt.
Revenind obtinem
f(x)=![]()
g(x)=x ![]()
![]()
In(x)=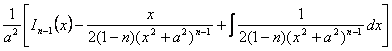
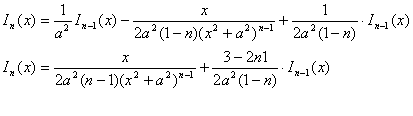
Primitivele functiilor rationale
I. Mai intai se scrie functia rationala sub forma unei sume in care pot interveni un polinom si functii rationale de forma:
(1) ![]()
(2) ![]()
Cum vom face acest lucru?
Reamintim ca o functie
rationala f este catul a doua functii polinomiale P si Q, adica f(x)=![]() . Daca grad P≥grad Q vom putea efectua impartirea si
vom obtine:
. Daca grad P≥grad Q vom putea efectua impartirea si
vom obtine:
P(x)=Q(x)C(x)+R(x) in care catul C(x) este polinom iar restul R(x) este tot un polinom cu grad R<grad Q. Aici functia rationala f se va scrie
![]()
In cazul in care grad P< grad Q vom scrie ![]() unde R(x)=P(x)
unde R(x)=P(x)
Pentru a scrie acum ![]() ca o suma de fractii de forma (1) si (2), vom proceda in
felul urmator:
ca o suma de fractii de forma (1) si (2), vom proceda in
felul urmator:
Daca polinomul Q are radacina reala "a"
avand ordinul de multiplicitate k in descompunerea lui ![]() vom avea termenii
vom avea termenii
![]()
Daca polinomul Q are radacinile complexe ![]() avand ordinul de
multiplicitate m atunci in descompunerea lui
avand ordinul de
multiplicitate m atunci in descompunerea lui ![]() vom avea fractiile:
vom avea fractiile:
![]()
unde b=-2 , c=x2+ 2. In final se vor determina constantele A1,A2,.B1,B2,..,C1,C2,
II. Acum ca functia rationala este scrisa ca suma dintre un polinom si functii rationale de forma (1) si (2) pentru a calcula primitiva unei functii rationale va trebui sa stim sa calculam primitivele functiilor polinomiale (ceea ce este clar daca utilizam liniaritatea operatorului de primitivare si prima formula din tabelul de primitive) si primitivele functiilor rationale de forma (1) si forma (2).
Vom avea:
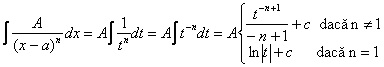
![]()
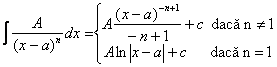
Apoi
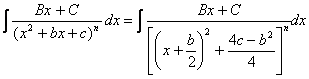
Cum b2-4c<0 vom
avea ![]() si vom putea nota
si vom putea nota ![]()
Vom face schimbarea de variabila ![]() . Atunci dx=dt. Revenind avem:
. Atunci dx=dt. Revenind avem:
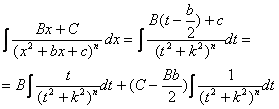
Prima integrala se va calcula cu schimbarea de variabila t2+k2=u iar a doua prin recurenta.
Exemple:
![]()
![]()
Numitorul se descompune in factori ireductibili
x4-10x2+9=(x2-1)(x2-9)=(x-1)(x+1)(x-3)(x+3)
Deci putem descompune fractia in franctii simple astfel:
![]() (1)
(1)
Inmultind relatia (1) cu x-1 obtinandu-se
![]()
dupa care trecem la limita cand x→1 si gasim A=1
Procedand la fel obtinem B=2; C=3; D=4.
Descompunerea in functii rationale simple este
![]()
integrand obtinem:
![]()
![]()
Primitivele unor functii irationale
Vom nota in continuare cu R o functie rationala ce poate fi de mai multe variabile.
I. Primitivarea functiei:
![]()
se reduce la primitivarea unei functii rationale facand schimbare de variabila
![]() unde n=c.m.m.m.c
unde n=c.m.m.m.c ![]()
Mai notam ca ![]() si
si ![]()
Exemplu:
![]()
Facem substitutia x=t6 deci dx=6t5dt.
Avem:

unde ![]()
Deci ![]()
I. Daca 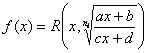 vom proceda asemanator
utilizand schimbarea de variabila.
vom proceda asemanator
utilizand schimbarea de variabila.
![]() unde n=c.m.m.m.c.
unde n=c.m.m.m.c.![]()
Exemplu:
![]()
Facem substitutia ![]()
Deci ![]()
Atunci:
![]()
Descompunem fractia in fractii simple si notam ![]() si obtinem
si obtinem
![]()
II.
R(x,![]() ) Vom calcula
) Vom calcula ![]() . Avem cazurile:
. Avem cazurile:
(A) ![]() atunci pentru ca radicalul sa aiba sens va rezulta a>0 si
atunci
atunci pentru ca radicalul sa aiba sens va rezulta a>0 si
atunci ![]()
(B) ![]() , caz in care a>0. Vom face schimbarea de variabila
, caz in care a>0. Vom face schimbarea de variabila
![]()

(C) ![]() Primitivele se cauta pe un interval pe care radicalul este definit si pe care nu se anuleaza
numitorul fractiei. Cum
Primitivele se cauta pe un interval pe care radicalul este definit si pe care nu se anuleaza
numitorul fractiei. Cum
![]()
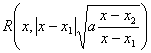
si am redus problema la cazul II, deci facem substitutia
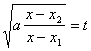
Exemplu:
![]()
2) ![]()
3)![]() , x>4
, x>4
Solutie: ![]() Cum
Cum ![]() , vom scrie
, vom scrie ![]() unde
unde ![]() este semnul lui x.
Atunci
este semnul lui x.
Atunci
![]()
2) ![]() Vom face schimbarea de
variabile
Vom face schimbarea de
variabile
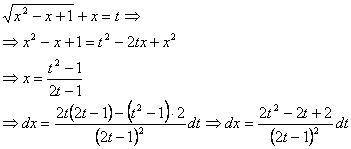
![]()
Dar
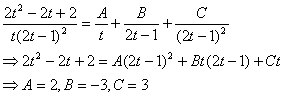
Deci
![]()
de unde
![]()
Daca facem in ultimele doua integrale schimbarea de variabila 2t-1=u(2dt=du) obtinem
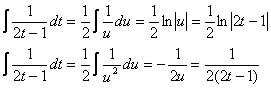
deci
![]()
In final avem
![]() 3)
3) ![]() si facem schimbarea de
variabila
si facem schimbarea de
variabila
![]()
![]()
![]() x
x![]()
Atunci
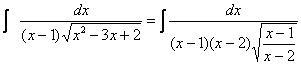
=![]()
Primitivele functiilor trigonometrice
Notam cu R(u,v) o functie rationala in variabile u si v. Pentru functia f(x)=R(sinx,
cosx) se face substitutia tg![]() =t si problema revine la calculul primitivei unei functii rationale.
Sa mai notam ca
=t si problema revine la calculul primitivei unei functii rationale.
Sa mai notam ca
sin
x=![]()
Sa precizam ca se aplica formula a II-a de schimbare de variabila acest lucru este
posibil pe un interval pe care functia ![]() este bijectiva. Prin
urmare aceasta metoda se aplica pe intervale de forma
este bijectiva. Prin
urmare aceasta metoda se aplica pe intervale de forma![]()
![]() .
.
Exemplu
![]()
![]()
Solutie :
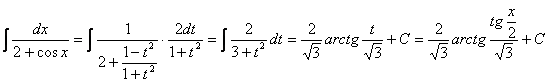
Daca dorim o primitiva pe R calculam saltul acestei "primitive" in punctele de forma (2k+1)π:

Vom avea:
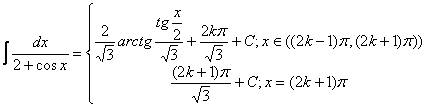
Observatie: Calculul primitivei poate fi simplificat in urmatoarele cazuri:
Exemplu
1) ![]()
2) ![]()
Solutie:
R(u,v)=u3v2; R(-u,v)=(-u)3v2=- u3v2=-R(u,v)
Prin urmare facem substitutia cos x=t ![]()
![]()
![]()
R(u,v)=![]() R(-u,-v)=
R(-u,-v)=![]()
Vom face substitutia tg x=t
![]() t
t![]() dx=
dx=![]()
![]() dx=
dx=![]()
![]() t=At
t=At![]() +A+B
+A+B![]()
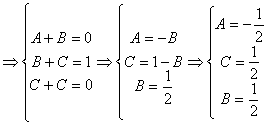
![]()
![]()
=-![]()
=-![]()
Copyright © 2025 - Toate drepturile rezervate