FUNCTII - proprietati

Paritate, imparitate

Multime simetrica: A se numeste simetrica daca xA, pentru A.

Functie para: f: AR, A = multime simetrica

f para: daca f(-x) = f(x), A

Interpretare grafica: graficul unei functii pare este simetric fata de axa Ox

Functie impara: f: AR, A = multime simetrica

f impara daca f(-x) = f(x), A

Interpretare grafica: graficul unei functii impare este simetric fata de origine.

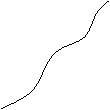
Monotonie f: AR

f este strict crescatoare daca: x< xf(x)<f(x),xA

f este strict descrescatoare daca: x< xf(x)>f(x),xA

f este crescatoare daca: xxf(x)f(x),xA

f este descrescatoare daca: x xf(x)f(x),xA

f este strict monotona daca f este strict crescatoare sau strict descrescatoare

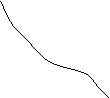
functie strict descrescatoare

f este monotona daca f este crescatoare sau descrescatoare

Raportul de variatie

pentru x: R(xx) =

Negarea monotoniei: pentru a demonstra ca f nu e monotona se cauta a, b, c A astfel incat a < b < c si f(a) < f(b) > f(c) sau f(a) > f(b) < f(c).

Interpretare grafica: o functie crescatoare are o alura crescatoare in sensul cresterii lui x si o functie descrescatoare are o alura descrescatoare in sensul cresterii lui x.

Proprietati

1) f, g strict crescatoare (descrescatoare) f + g strict crescatoare (descrescatoare)

2) a > 0 si f strict crescatoare (descrescatoare) af strict crescatoare (descrescatoare)

a < 0 si f strict crescatoare (descrescatoare) af strict descrescatoare (crescatoare)

caz particular: f strict crescatoare - f strict descrescatoare

f strict descrescatoare - f strict descrescatoare

3) Daca f, g sunt pozitive si strict crescatoare (descrescatoare) g strict crescatoare (descrescatoare)

4) Daca f > 0 si f strict crescatoare (descrescatoare) este strict descrescatoare (crescatoare)

5) (,,regula semnelor'') Daca f, g sunt crescatoare atunci fg este crescatoare

Daca f, g sunt descrescatoare atunci fg este crescatoare

Daca f si g au monotonii diferite g este descrescatoare

6) Daca f este strict crescatoare si g este strict descrescatoareecuatia f(x) = g(x) are cel mult o solutie.

Injectivitate: f: AB

f injectiva daca: xxf(x)f(x),A

Observatie: f injectiva: f(x) = f(x)x = x,A

practic: fie xxA astfel incat f(x) = f(x). Se demonstreaza ca x = xf injectiva.

Proprietati: f injectiva ecuatia f(x) = y are cel mult o solutie.

Interpretare grafica: f injectivaorice paralela la Ox taie graficul in cel mult un punct.

Noninjectivitate: se cauta x, x astfel incat xx, dar f(x)f(x).

Proprietati

1) f strict monotona f injectiva.

2) f, g injectiva gf injectiva

3) gf injectivaf injectiva.

Observatie: Orice functie are cel putin o restrictie injectiva.

Surjectivitate: f:AB

f surjectiva daca pentru B, A astfel incat f(x) = y

Proprietate: f surjectivamf = B

Practic: fie yB astfel incat f(x) = y. Se afla x si se verifica xA. Atunci f este surjectiva.

Proprietate: f surjectiva ecuatia f(x) = y are cel putin o solutie in A.

Interpretare grafica: f surjectivaorice paralela la Ox, dusa prin codomeniu, taie graficul in cel putin un punct.

Nonsurjectivitate: Se demonstreaza ca ImfB sau se cauta yB astfel incat f(x) y,A.

Proprietati

1) f, g surjectivef surjectiva

2) gf surjectivag surjectiva

Observatie: Orice functie are o singura corestrictie surjectiva.

Bijectivitate: f:AB

f este bijectiva daca f este injectiva si surjectiva

Proprietate: f bijectiva ecuatia f(x) = y are solutie unica.

Interpretare grafica: f bijectiva orice paralela la Ox care trece prin codomeniu taie graficul intr-un unic punct.

Nonbijectivitate: se demonstreaza ca functia nu e bijectiva sau surjectiva.

Proprietate:

1) f, g bijectivagf bijectiva

2) gf surjectivaf injectiva si g surjectiva

Observatie: Orice functie poate fi restrictionata si corestrictionata la o functie bijectiva.