 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
Logica Predicatelor
1. Alfabetul si sintaxa in logica predicatelor
Vom prezenta logica predicatelor ca un limbaj formal, ca si logica propozitiilor. Reamintim ca un limbaj formal este format, in general, dintr-un alfabet care contine toate simbolurile limbajului, o sintaxa care stabileste modul in care sunt folosite simbolurile limbajului pentru a forma cu ele formule ( aceste formule, in logica propozitiilor, s-au numit propozitii) si o semantica care stabileste interpretarea acestor formule.
Alfabetul. In logica propozitiilor alfabetul este format din trei categorii de simboluri:
a) Simboluri logice:
i) Variabile
care se vor nota cu litere mici de la sfarsitul alfabetului latin,
insotite eventual de indici: ![]() ,etc.
,etc.
ii) Simboluri ale conectorilor logici: ![]() .
.
iii) Un simbol , numit virgula, un simbol ( , numit paranteza deschisa si un simbol, ), numit paranteza inchisa.
iv) Cuantificatori:![]() .
.
b) Simboluri specifice:
i) Simboluri de predicate care se vor nota cu litere mari ale alfabetului latin de
tipul P, Q, ![]() ,, etc.
,, etc.
ii) Simboluri de constante care se vor nota cu litere mici de la inceputul
alfabetului latin: a , b, ![]() ,,etc.
,,etc.
iii) Simboluri de functii care se vor nota cu litere mici ale alfabetului latin
de tipul ![]() g,
g, ![]() ,,etc.
,,etc.
Cuantificatorii ![]() si
si ![]() se numesc respectiv cuantificatorul universal si cuantifcatorul existential.
se numesc respectiv cuantificatorul universal si cuantifcatorul existential.
Mentionam ca
predicatele, ca si funtiile, se disting intre ele prin aritatea lor, aritate care trebue
sa fie un numar intreg pozitiv; respectiv vom avea simboluri de
predicate sau simboluri de functii,
unare, binare, ternare, , ![]() are,, etc. Din punct de vedere formal aritatea nu se
defineste ci se mentioneaza la fiecare aparitie a unui
simbol de predicat sau de functie. Din comoditate vom spune in loc de
simboluri de constante sau simboluri de variabile pur si simplu constante,
respectiv variabile.
are,, etc. Din punct de vedere formal aritatea nu se
defineste ci se mentioneaza la fiecare aparitie a unui
simbol de predicat sau de functie. Din comoditate vom spune in loc de
simboluri de constante sau simboluri de variabile pur si simplu constante,
respectiv variabile.
Sintaxa. Orice secventa de simboluri se numesre expresie. Printre expresii distingem unele care se numesc termeni, formule atomice( atomi), formule, formule inchise( fraze).
Notiunea de termen se defineste inductiv astfel;
i) Orice variabila si orice constanta sunt termeni.
ii) Daca f este un simbol de
functie ![]() ara si
ara si ![]() sunt termeni atunci
sunt termeni atunci ![]() este un termen.
este un termen.
iii) Orice termen se obtine aplicand succesiv, de un numar finit de ori, regulile i) si ii).
Notiunea de formula atomica: O formula atomica este o
expresie de forma ![]() unde P este un simbol de predicat
unde P este un simbol de predicat ![]() ar si
ar si ![]() sunt termeni.
sunt termeni.
Notiunea de formula se defineste inductiv astfel:
i) Orice formula atomica este o formula.
ii) Daca ![]() si
si ![]() sunt formule atunci
sunt formule atunci ![]() sunt formule.
sunt formule.
iii) Daca ![]() este o formula
si
este o formula
si ![]() este o variabila
atunci
este o variabila
atunci ![]() si
si ![]() sunt formule.
sunt formule.
iv) Orice formula se obtine aplicand succesiv, de un numar finit de ori, regulile i) si ii) si iii).
In ![]() formula
formula ![]() se numeste scopul cuantificatorului
se numeste scopul cuantificatorului ![]() si, analog, in
si, analog, in ![]() formula
formula ![]() se numeste scopul cuantificatorului
se numeste scopul cuantificatorului ![]() . Notam, de asemenea, ca in
. Notam, de asemenea, ca in ![]() sau
sau ![]() variabila
variabila ![]() poate sa
lipseasca din expresia lui
poate sa
lipseasca din expresia lui ![]() ; in acest caz, dupa cum vom vedea, din punct de vedere
semantic,
; in acest caz, dupa cum vom vedea, din punct de vedere
semantic, ![]() si
si ![]() , au aceeasi semnificatie ca si
, au aceeasi semnificatie ca si ![]() .
.
Parantezele se poate reduce dupa aceleasi reguli ca si in logica propozitiilor
- mai intai se reduc parantezele
exterioare; astfel ![]() devine
devine ![]() ,
, ![]() devine
devine ![]() , etc.
, etc.
- ordinea de prioritate a
aplicarii conectorilor logici si a cuantificatorilor ![]() si
si ![]() este:
este:
![]()
Iar
in cazul aparitiei multiple ale aceluiasi cuantificator acesta, cu
exceptia negatiei, se aplica de la dreapta la stanga.
Astfel ![]() devine
devine ![]() .
.
-
daca avem mai multe aparitii succesive ale cuantificatorilor, acesia
se aplica de la stanga la dreapta fara a mai mentona acest
lucru prin paranteze. Astfel ![]() devine
devine ![]() .
.
Exemple
1.![]() se obtine prin reducerea
parantezelor din
se obtine prin reducerea
parantezelor din ![]() .
.
2.![]() se obtine prin reducerea
parantezelor din
se obtine prin reducerea
parantezelor din ![]() .
.
3.![]() se obtine prin reducerea parantezelor
din
se obtine prin reducerea parantezelor
din ![]() .
.
4.
Pentru a indica un limbaj concret
este suficient sa indicam simbolurile sale specifice. Astfel putem
considera un limbaj ![]() care contine
doua constante 0 si 1, doua predicate binare
care contine
doua constante 0 si 1, doua predicate binare ![]() si
si ![]() , o functie binara +. In acest limbaj putem
considera urmatorele formule:
, o functie binara +. In acest limbaj putem
considera urmatorele formule:
![]() ,
, ![]() ,
, 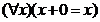 ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Mentionam
ca am notat, pentru orice doi termeni u
si v, ![]() in loc de
in loc de ![]() ,
, ![]() in loc de
in loc de ![]() si
si ![]() in loc de
in loc de ![]()
Exercitii.
1. Refaceti parantezele pentru urmatoarele formule
(a) ![]() .
.
![]() ;
; ![]() .
.
(b) ![]() .
.
![]() ;
; ![]() .
.
(c) ![]() .
.
![]() ;
; ![]() .
.
(d) ![]() .
.
![]() ;
; ![]() ..
..
(e) ![]() .
.
![]() .
.
(f) ![]() .
.
![]() ;
; ![]() .
.
(g) ![]() .
.
![]()
2. Reduceti cat mai multe paranteze posibile in urmatoarele formule.
a) ![]() .
.
![]() .
.
(b) ![]() .
.
![]() .
.
(c) ![]()
![]()
O aparitie a unei variabile x intr-o formula ![]() se numeste legata daca aparitia lui x este intr-un cuantificator,
se numeste legata daca aparitia lui x este intr-un cuantificator, ![]() sau
sau ![]() , sau in scopul unui
cuantificator,
, sau in scopul unui
cuantificator, ![]() sau
sau ![]() din
din ![]() . In caz contrar aparitia se numeste libera in
. In caz contrar aparitia se numeste libera in ![]() . O variabila se numeste legata( respectiv libera)
intr-o formula
. O variabila se numeste legata( respectiv libera)
intr-o formula ![]() daca are cel putin o aparitie legata(
respectiv libera) in
daca are cel putin o aparitie legata(
respectiv libera) in ![]() .
.
Exemple.
1. ![]() .
.
2.
![]() .
.
3. ![]() .
.
4.
![]()
In exemplul 1
singura aparitie a lui x este
libera. In exemplul 2, prima aparitie a lui x este libera dar a doua aparitie a lui x ca si a treia sunt legate. In
exemplul 3, toate aparitiile lui ![]() sunt legate. In
exemplul 4, x are o singura
aparitie care este legata. In fiecare dintre exemplele de mai sus
variabila y are o singura
aparitie care este libera. In exemplul 2, variabila
sunt legate. In
exemplul 4, x are o singura
aparitie care este legata. In fiecare dintre exemplele de mai sus
variabila y are o singura
aparitie care este libera. In exemplul 2, variabila ![]() este atat legata
cat si libera
este atat legata
cat si libera
Exercitii
1. Indicati aparitiile libere si legate ale variabilelor in urmatoarele formule:
(a) ![]() .
.
x are doua aparitii legate; y o aparitie libera; z doua aparitii legate.
(b) ![]()
Primele doua aparitii ale lui y sunt legate si a treia este libera; prima aparitie a lui z este libera si celelalte doua sunt legate.
(c) ![]()
Toate aparitiile lui x sunt legate; y are primele trei aparitii legate si a treia libera.
Pentru orice formula ![]() vom scrie
vom scrie ![]() in loc de
in loc de ![]() pentru a indica
ca
pentru a indica
ca ![]() nu are alte variabile
libere in afara de
nu are alte variabile
libere in afara de ![]() ( ceea ce nu inseamna ca
( ceea ce nu inseamna ca ![]() contine
neaparat aceste variabile libere). Notatia este convenabila
deoarece vom consimti sa scriem
contine
neaparat aceste variabile libere). Notatia este convenabila
deoarece vom consimti sa scriem ![]() pentru rezultatul substitutiilor variabilelor
pentru rezultatul substitutiilor variabilelor ![]() cu termenii
cu termenii ![]() in toate
apatitiile libere(daca exista) ale lui
in toate
apatitiile libere(daca exista) ale lui ![]() respectiv.
respectiv.
2. Interpretari
Formulele din limbajul logicii predicatelor nu au sens decat daca se da o anumita interpretare simbolurilor limbajului. O interpretare I consta din urmatoarele:
i) O multime D numita domeniul interpretarii.
ii) Pentru fiecare simbol de predicat ![]() ar P, o
relatie
ar P, o
relatie ![]() ara
ara ![]() intre elementele lui D.
intre elementele lui D.
iii) Pentru fiecare simbol de
functie ![]() ara f, o
functie
ara f, o
functie ![]() ara
ara ![]() .
.
iv) Pentru fiecare simbol de
constanta a, un element ![]() .
.
Pentru fiecare simbol de predicat P, simbol de functie f, simbol de constanta a, relatia ![]() , functia
, functia ![]() si elementul
si elementul ![]() se numesc interpretarile lui P, f,
a in raport cu interpretarea I a limbajului si daca
interpretarea I este clara din
context nu se mai face distinctie intre simbol si inerpretarea sa.
se numesc interpretarile lui P, f,
a in raport cu interpretarea I a limbajului si daca
interpretarea I este clara din
context nu se mai face distinctie intre simbol si inerpretarea sa.
O formula care nu contine variabile libere se numeste formula inchisa sau fraza. Putem considera ca frazele sunt propozitii care in raport cu o interpretare data sunt adevarate sau false. Formulele in general pot fi( in raport cu o interpretare data) adevarate( satisfacute) pentru anumite valori ale variabilelor libere in domeniu de interpretare si false pentru alte valori ale lor.
Exemple. Consideram urmatoarele formule
1.
![]() .
.
2.
![]() .
.
3. ![]()
Consideram
o intrepretare I in care domeniul
interpretarii este multimea ![]() a numerelor intregi
pozitive iar interpretarea predicatului binar P este relatia de ordine pe
a numerelor intregi
pozitive iar interpretarea predicatului binar P este relatia de ordine pe ![]() ; deci daca
; deci daca ![]() atunci
atunci ![]() daca
daca ![]() . Formula 1 reprezinta atunci o expresie in limbajul
cotidian, anume
. Formula 1 reprezinta atunci o expresie in limbajul
cotidian, anume ![]() (
( ![]() x este mai mic sau
egal ca y
x este mai mic sau
egal ca y![]() ) care este satisfacuta de anumite perechi
) care este satisfacuta de anumite perechi ![]() de numere intregi
pozitive ( de exemplu avem
de numere intregi
pozitive ( de exemplu avem ![]() si
si ![]() deci perechile
deci perechile ![]() si
si ![]() satisfac formula
noastra) si nu este satisfacuta de altele ( de exemplu avem
satisfac formula
noastra) si nu este satisfacuta de altele ( de exemplu avem ![]() deci perechea
deci perechea ![]() nu satisface formula. Formula 2 reprezinta expresia
nu satisface formula. Formula 2 reprezinta expresia ![]() pentru orice numar intrg pozitiv y ,
pentru orice numar intrg pozitiv y , ![]()
![]() si este
satisfacuta numai de numarul 1. Formula 3 este insa o
fraza care afirma ca exista un cel mai mic numar
intreg pozitiv si este adevarata in interpretarea noastra.
Daca insa domeniul interpretarii este multimea
si este
satisfacuta numai de numarul 1. Formula 3 este insa o
fraza care afirma ca exista un cel mai mic numar
intreg pozitiv si este adevarata in interpretarea noastra.
Daca insa domeniul interpretarii este multimea ![]() a numerelor intregi
atunci fraza noastra nu mai este adevarata.
a numerelor intregi
atunci fraza noastra nu mai este adevarata.
Exercitiu
Pentru urmatoarele formule si pentru interpretarile indicate stabiliti pentru ce valori ale variabilelor libere aceste formule sunt satisfacute sau, in cazul cand ele sunt fraze, daca ele sunt adevarate
(i) ![]() ;
;
(ii) ![]() ;
;
(iii) ![]() .
.
(a) Domeniul interpretarii este
multimea ![]() a numerelor intregi
pozitive, interpretarea predicatului binar P
este relatia de ordine pe
a numerelor intregi
pozitive, interpretarea predicatului binar P
este relatia de ordine pe ![]() , interpretarea functiei binare f este inmultirea pe
, interpretarea functiei binare f este inmultirea pe ![]() si interpretarea
constantei a este
si interpretarea
constantei a este ![]() .
.
(b) Domeniu interpretarii este
multimea ![]() a numerelor intregi,
interpretarea predicatului binar P
este relatia de egalitate pe
a numerelor intregi,
interpretarea predicatului binar P
este relatia de egalitate pe ![]() si interpretarea
constantei a este
si interpretarea
constantei a este ![]() .
.
(iii) Domeniul inerpretarii este
multimea ![]() a tuturor
submultimilor lui
a tuturor
submultimilor lui ![]() ,
, ![]() inseamna
inseamna ![]() ,
, ![]() inseamna
inseamna ![]() iar a inseamna multimea vida
iar a inseamna multimea vida ![]() .
.
Rezolvare
(a) Formula (i) este expresia ![]() care este satisfacuta de toate perechile
care este satisfacuta de toate perechile ![]() de numere intregi
pozitive cu
de numere intregi
pozitive cu ![]() si nu este satisfacuta de perechea
si nu este satisfacuta de perechea ![]() .
.
Formula (ii) este expresia ![]() . O pereche
. O pereche ![]() de numere intregi
pozitive astfel ca
de numere intregi
pozitive astfel ca ![]() satisface formula
daca si numai daca
satisface formula
daca si numai daca ![]() .
.
Formula (iii) este insa o
fraza care afirma ca relatia de ordine pe ![]() este tranzitiva
si este evident adevarata.
este tranzitiva
si este evident adevarata.
In continuare vom defini notiunile semantice de adevar sau satisfactie intr-un mod precis.
Fie I
o interpretare.O asociere in interpretarea I este o aplicatie
![]() unde
unde ![]() este multimea tuturor variabilelor si D este domeniul interpretarii. Fie
este multimea tuturor variabilelor si D este domeniul interpretarii. Fie ![]() o asociere in
interpretarea M . Notam cu
o asociere in
interpretarea M . Notam cu ![]() multimea tuturor
termenilor si definim o aplicatie
multimea tuturor
termenilor si definim o aplicatie ![]() inductiv astfel:
inductiv astfel:
i) Pentru orice constanta c luam ![]() .
.
ii) Pentru orice variabila x luam ![]() .
.
iii) Daca f este o functie ![]() ara si
ara si ![]() sunt termeni atunci
sunt termeni atunci ![]() .
.
Aplicatia ![]() se noteaza cu
aceeasi litera
se noteaza cu
aceeasi litera ![]() ca si asocierea
data. Spunem, de asemenea ca
ca si asocierea
data. Spunem, de asemenea ca ![]() este elementul din D asociat
termenului
este elementul din D asociat
termenului ![]() .
.
Exemplu.
Consideram termenul ![]() unde f si g sunt functii binare,
unde f si g sunt functii binare, ![]() si
si ![]() variabile si a o constanta. Consideram
interpretarea I cu domeniul
multimea
variabile si a o constanta. Consideram
interpretarea I cu domeniul
multimea ![]() a numerelor intregi,
functia f interpretata ca
inmultirea numerelor intregi, functia g interpretata ca adunarea numerelor intregi si constanta
a interpretata ca numarul
intreg 2. Pentru o pereche
a numerelor intregi,
functia f interpretata ca
inmultirea numerelor intregi, functia g interpretata ca adunarea numerelor intregi si constanta
a interpretata ca numarul
intreg 2. Pentru o pereche ![]() de numere intregi
putem considera o asociere
de numere intregi
putem considera o asociere ![]() cu
cu ![]() si
si ![]() . Atunci asociatul termenului
. Atunci asociatul termenului ![]() este numarul
intreg
este numarul
intreg ![]() .
.
Faptul ca o asociere ![]() satisface o formula
satisface o formula ![]() se defineste
se defineste![]() inductiv astfel
inductiv astfel
i) Daca ![]() este o formula
atomica atunci
este o formula
atomica atunci ![]() unde P este un predicat
unde P este un predicat ![]() ar si
ar si ![]() sunt termeni; in acest
sunt termeni; in acest
![]() satisface
satisface ![]() daca
daca ![]() .
.
ii) Daca ![]() si
si ![]() sunt formule atunci
sunt formule atunci
a) ![]() satisface
satisface ![]() daca
daca ![]() nu satisface
nu satisface ![]() ;
;
b) ![]() satisface
satisface ![]() daca
daca ![]() satisface
satisface ![]() si
si ![]() satisface
satisface ![]() ;
;
c) ![]() satisface
satisface ![]() daca
daca ![]() satisface
satisface ![]() sau
sau ![]() satisface
satisface ![]() ;
;
d) ![]() satisface
satisface ![]() daca
daca ![]() nu satisface
nu satisface ![]() sau
sau ![]() satisface
satisface ![]() ;
;
e) ![]() satisface
satisface ![]() daca
daca ![]() satisface
satisface ![]() si
si ![]() satisface
satisface ![]() sau
sau ![]() nu satisface
nu satisface ![]() sau
sau ![]() nu satisface
nu satisface ![]() si
si ![]() nu satisface
nu satisface ![]() .
.
iii) Daca ![]() este o formula
si x este o variabila
atunci
este o formula
si x este o variabila
atunci
a) ![]() satisface
satisface ![]() daca pentru orice
element
daca pentru orice
element ![]() asocierea
asocierea ![]() definita prin
definita prin
![]()
satisface
![]() .
.
b) ![]() satisface
satisface ![]() daca exista
un element
daca exista
un element ![]() astfel incat asocierea
astfel incat asocierea
![]() de mai sus satisface
de mai sus satisface ![]() .
.
Putem reformula definitia de mai
sus definind pentru fiecare asociere ![]() o valorizare
o valorizare ![]() astfel: pentru
astfel: pentru ![]() luam
luam ![]() daca
daca ![]() satisface
satisface ![]() si
si ![]() daca
daca ![]() nu satisface
nu satisface ![]() . Atunci punctele i), ii) si iii) ale definitiei se
transcriu astfel:
. Atunci punctele i), ii) si iii) ale definitiei se
transcriu astfel:
i) Daca ![]() este o formula
atomica,
este o formula
atomica, ![]() unde P este un predicat
unde P este un predicat ![]() ar si
ar si ![]() sunt termeni atunci
sunt termeni atunci ![]() daca si
numai daca
daca si
numai daca ![]() .
.
ii) Daca ![]() si
si ![]() sunt formule atunci
sunt formule atunci
![]()
![]() .
.
iii) Daca ![]() este o formula
si x este o variabila
atunci
este o formula
si x este o variabila
atunci ![]() daca si
numai daca pentru orice
daca si
numai daca pentru orice ![]() avem
avem ![]() si
si ![]() daca si
numai daca exista un
daca si
numai daca exista un ![]() astfel incat
astfel incat![]() .
.
Fie I
o interpretare. Daca ![]() este o fraza(
formula inchisa) atunci, evident, pentru orice doua asocieri
este o fraza(
formula inchisa) atunci, evident, pentru orice doua asocieri ![]() ( unde D este
domeniul interpretarii) avem
( unde D este
domeniul interpretarii) avem ![]() motiv pentru care
scriem
motiv pentru care
scriem ![]() unde
unde ![]() este o asociere
oarecare. In ceea ce urmeaza vom studia din punct de vedere semantic numai
frazele. Motivul este ca de regula, din punct de vedere semantic,
formulele care nu sunt inchise pot fi inlocuite cu fraze. Astfel avem:
este o asociere
oarecare. In ceea ce urmeaza vom studia din punct de vedere semantic numai
frazele. Motivul este ca de regula, din punct de vedere semantic,
formulele care nu sunt inchise pot fi inlocuite cu fraze. Astfel avem:
Fie
![]() o formula care nu
este neaparat inchisa. Atunci, evident
o formula care nu
este neaparat inchisa. Atunci, evident ![]() si
si ![]() sunt fraze si
avem
sunt fraze si
avem
1. Exista o asociere ![]() astfel incat
astfel incat ![]() daca si
numai daca
daca si
numai daca ![]() .
.
2. Pentru orice asociere ![]() avem
avem ![]() daca si
numai daca
daca si
numai daca ![]() .
.
O fraza ![]() se numeste
adevarata in interpretarea I daca
se numeste
adevarata in interpretarea I daca
![]() ; in aceasta situatie spunem, de asemenea, ca
interpretarea I este un model pentru
; in aceasta situatie spunem, de asemenea, ca
interpretarea I este un model pentru ![]() si notam
si notam ![]() . Fraza
. Fraza ![]() se numeste
falsa in interpretarea I
daca
se numeste
falsa in interpretarea I
daca ![]() . Fraza
. Fraza ![]() se numeste logic adevarata ( tautologie) daca este adevarata in orice
interpretare, caz in care sctriem
se numeste logic adevarata ( tautologie) daca este adevarata in orice
interpretare, caz in care sctriem ![]() , si logic
falsa ( contradictie) daca este falsa in orice
interpretare).
, si logic
falsa ( contradictie) daca este falsa in orice
interpretare).
Exemple(analiza semantica a unor fraze)
Fraza ![]() este logic
adevarata. Intr-adevar, In caz contrar ar exista o interpretare I astfel incat
este logic
adevarata. Intr-adevar, In caz contrar ar exista o interpretare I astfel incat ![]() este falsa in
aceasta interpretare adica
este falsa in
aceasta interpretare adica ![]() este adevarata si
este adevarata si ![]() este falsa. Interpretarea predicatului unar
este falsa. Interpretarea predicatului unar ![]() este o submultime
este o submultime
![]() si interpretarea
constantei
si interpretarea
constantei ![]() este elementul
este elementul ![]() si, in
particular, faptul ca
si, in
particular, faptul ca ![]() este falsa in I
inseamna ca
este falsa in I
inseamna ca ![]() . Pe de alta parte faptul ca
. Pe de alta parte faptul ca ![]() este adevarata inseamna ca
este adevarata inseamna ca ![]() pentru orice element
pentru orice element ![]() . Evident, avem o contradictie.
. Evident, avem o contradictie.
2.
Consideram fraza![]() . Fie I o
interpretare oarecare. Interpretarea predicatului binar P este o relatie binara
. Fie I o
interpretare oarecare. Interpretarea predicatului binar P este o relatie binara ![]() . Faptul ca fraza
. Faptul ca fraza ![]() este adevarata
in I inseamna ca pentru orice elemente
este adevarata
in I inseamna ca pentru orice elemente ![]() daca
daca ![]() atunci
atunci ![]() . Astfel fraza
. Astfel fraza ![]() este
adevarata intr-o interpretare I
daca si numai daca interpretarea predicatului binar P este o relatie binara
simetrica pe domenul D al
interpretarii.
este
adevarata intr-o interpretare I
daca si numai daca interpretarea predicatului binar P este o relatie binara
simetrica pe domenul D al
interpretarii.
Analog fraza ![]() este
adevarata intr-o interpretare I
daca si numai daca interpretarea predicatului binar P este o relatie binara
reflexiva pe domenul D al
interpretarii, fraza
este
adevarata intr-o interpretare I
daca si numai daca interpretarea predicatului binar P este o relatie binara
reflexiva pe domenul D al
interpretarii, fraza ![]() este
adevarata intr-o interpretare I
daca si numai daca interpretarea predicatului binar P este o relatie binara
tranzitiva pe domenul D al
interpretarii; in fine fraza
este
adevarata intr-o interpretare I
daca si numai daca interpretarea predicatului binar P este o relatie binara
tranzitiva pe domenul D al
interpretarii; in fine fraza
![]()
este adevarata intr-o interpretare I daca si numai daca interpretarea predicatului binar P este o relatie de echivalenta pe domenul D al interpretarii.
3. Consideram fraza ![]() . Fie I o
interpretare oarecare si presupunem ca interpretarea predicatului
binar Q este relatia de
egalitate pe D. Atunci fraza
. Fie I o
interpretare oarecare si presupunem ca interpretarea predicatului
binar Q este relatia de
egalitate pe D. Atunci fraza ![]() este
adevarata in I daca
si numai daca interpretarea predicatului binar P este graficul unei aplicatii
este
adevarata in I daca
si numai daca interpretarea predicatului binar P este graficul unei aplicatii ![]() .
.
5.
Consideram fraza ![]() . Consideram o interpretare I cu domeniul interpretarii
. Consideram o interpretare I cu domeniul interpretarii ![]() si interpretarea
predicatului binar relatia de prdine
si interpretarea
predicatului binar relatia de prdine ![]() pe
pe ![]() . Atunci fraza
. Atunci fraza ![]() este
adevarata in I daca
si numai daca interpretarea constantei a este numarul natural 0. Rezulta, de asemenea, ca
fraza
este
adevarata in I daca
si numai daca interpretarea constantei a este numarul natural 0. Rezulta, de asemenea, ca
fraza ![]() este adevarata in interpretarea de mai sus.
Daca schimbam domeniul interpretarii si anume il luam
este adevarata in interpretarea de mai sus.
Daca schimbam domeniul interpretarii si anume il luam ![]() atunci fraza
atunci fraza ![]() nu este
adevarata pentru orice interpretare a constantei a si, in particular fraza
nu este
adevarata pentru orice interpretare a constantei a si, in particular fraza ![]() nu este adevarata.
nu este adevarata.
Echivalenta frazelor se
defineste exact ca si in logica propozitiilor mai precis pentru
orce doua fraze ![]() avem
avem ![]() daca
daca ![]() iar echivalenta
ferzelor are aceleasi proprietati ca si echivalenta
propozitiilor.
iar echivalenta
ferzelor are aceleasi proprietati ca si echivalenta
propozitiilor.
Tablouri semantice.
Sintaxa frazelor se poate formula independent de sintaxa formulelor in general pe baza urmatoarelor definitii:
Un termen de baza este un termen in expresia caruia nu apar variabile.
O fraza
atomica este o expresie de forma ![]() unde P este un simbol de predicat
unde P este un simbol de predicat ![]() ar si
ar si ![]() sunt termeni de
baza.
sunt termeni de
baza.
Notiunea de fraza se poate defini inductiv astfel:
i) Orice fraza atomica este o fraza.
ii) Daca ![]() si
si ![]() sunt fraze atunci
sunt fraze atunci ![]() sunt fraze.
sunt fraze.
iii) Daca ![]() este o formula
unde
este o formula
unde ![]() este o variabila
atunci
este o variabila
atunci ![]() si
si ![]() sunt fraze.
sunt fraze.
iv) Orice fraza se obtine aplicand succesiv, de un numar finit de ori, regulile i) si ii) si iii).
Tablourile semantice atomice sunt:
![]() Pentru fiecare
fraza atomica
Pentru fiecare
fraza atomica ![]() ,
,
(1) ![]() si (2)
si (2)![]() ;
;
![]() Pentru fraza
Pentru fraza ![]() ,
,
(3) ![]() si (4)
si (4) 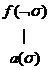 ;
;
![]() Pentru orice fraze
Pentru orice fraze ![]() ,
,
(5)
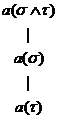 si (6)
si (6) 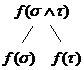 ;
;
(7) 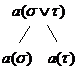 si (8)
si (8) 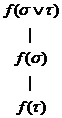 ;
;
(9) 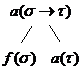 si (10)
si (10) 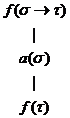 ;
;
(11) 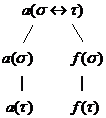 si (12)
si (12) 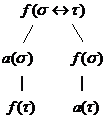 ;
;
![]() Pentru orice formula
Pentru orice formula ![]() ,
,
(13) 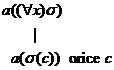 (14)
(14) 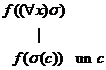 ;
;
(15) 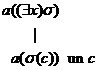 (16)
(16) 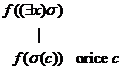 .
.
Acum putem demonstra, cu ajutorul tablourilor semantice( demonstratii Beth), ca anumite fraze din logica propozitiilor sunt logic adevarate , teorema de corectitudine fiind evidenta; insa datorita faptului ca tablourile semantice in logica predicatelor pot sa fie infinite, nu mai functioneaza o teorema de completitudine clara, ca cea din logica propozitiilor.
(1)
![]() ( pe scurt
( pe scurt![]() ),
),
(2) ![]() ( pe scurt si
( pe scurt si
![]() ),
),
unde ![]() si
si ![]() .
.
Pentru afirmatia (1) demonstratia Beth este
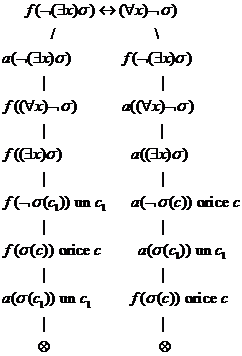
Afirmatia (2) rezulta din (1) prin echivalente astfel:
![]() ( deoarece
( deoarece ![]() prin legea dublei
negatii)
prin legea dublei
negatii)
![]() ( deoarece, conform lui (1),
( deoarece, conform lui (1), ![]() )
)
![]() ( prin legea dublei negatii).
( prin legea dublei negatii).
(3)
![]() ( pe scurt
( pe scurt ![]() ),
),
(4) ![]() ( pe scurt
( pe scurt ![]() ),
),
unde ![]() si
si ![]() .
.
(3) si (4) rezulta prin echivalente din (1):
![]() ( deoarece, conform lui (1),
( deoarece, conform lui (1), ![]() )
)
![]() ( deoarece
( deoarece ![]() prin legea dublei
negatii);
prin legea dublei
negatii);
![]() ( deoarece, conform lui (2),
( deoarece, conform lui (2), ![]() )
)
![]() ( deoarece
( deoarece ![]() prin legea dublei
negatii).
prin legea dublei
negatii).
(5)
![]() (
distributivitatea completa a cuantificatorului universal fata de
conjunctie),
(
distributivitatea completa a cuantificatorului universal fata de
conjunctie),
(6)
![]() ( distributivitatea
completa a cuantificatorului existential fata de
disjunctie).
( distributivitatea
completa a cuantificatorului existential fata de
disjunctie).
Pentru afirmatia (5) vom da mai jos o demonstratie Beth. Afirmatia (6) rezulta prin echivalente astfel:
![]() ( deoarece, conform lui (4),
( deoarece, conform lui (4),![]() )
)
![]() ( deoarece, conform lui De Morgan,
( deoarece, conform lui De Morgan,![]() )
)
![]() ( conform lui (5)
( conform lui (5)
![]() ( conform lui De Morgan)
( conform lui De Morgan)
![]() ( deoarece, conform lui (4),
( deoarece, conform lui (4), ![]() ).
).

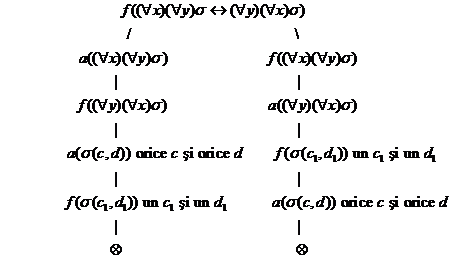
(7)![]()
(8)![]()
(9)![]() este logic adevarata
este logic adevarata
(10)
![]() nu este logic
adevarata; aici
nu este logic
adevarata; aici ![]() .
.
Pentru (7) urmeaza demonstratie Beth
Pentru (8) procedam prin echivalete astfel:
![]() prin legea dublei
negatii)
prin legea dublei
negatii)
![]() ( deoarece, conform lui (2),
( deoarece, conform lui (2), ![]() )
)
![]() ( deoarece, conform lui (2),
( deoarece, conform lui (2), ![]() )
)
![]() ( conform lui (7))
( conform lui (7))
![]() ( deoarece, conform lui (1),
( deoarece, conform lui (1), ![]() )
)
![]() ( deoarece, conform lui (1),
( deoarece, conform lui (1), ![]() )
)
![]() ( conform legii dublei negatii).
( conform legii dublei negatii).
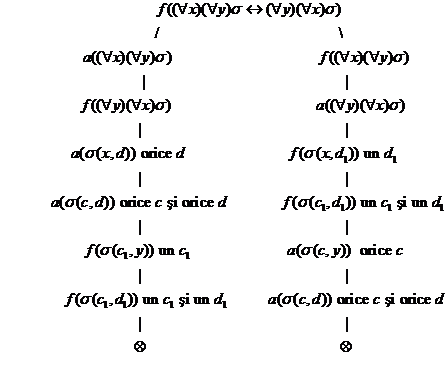
Pentru (9) urmeaza demonstratie Beth
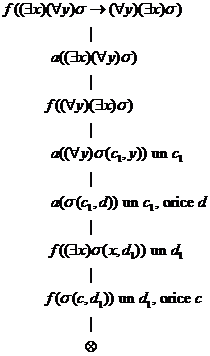
Pentru a
demonstra (10) consideram formula ![]() unde P este un predicat binar si
interpretarea I cu domeniul
multimea
unde P este un predicat binar si
interpretarea I cu domeniul
multimea ![]() a numerelor naturale
si predicatul P relatia de
egalitate pe
a numerelor naturale
si predicatul P relatia de
egalitate pe ![]() . Atunci, interpretarea formulei
. Atunci, interpretarea formulei ![]() este
este ![]() , interpretarea formulei
, interpretarea formulei ![]() este
este ![]() si avem, evident,
si avem, evident,
![]() ,
, ![]()
si deci
![]() .
.
Insa este instructiv de vazut si de ce demonstrata Beth esueaza.
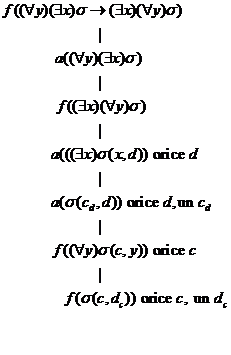
Cuantificatorul universal are o distributivitate partiala fata de disjunctie iar cuantificatorul existential are o distributivitate partiala fata de conjunctie
(11)
![]() este logic
adevarata,
este logic
adevarata,
(12) ![]() nu este logic
adevarata,
nu este logic
adevarata,
(13) ![]() este logic
adevarata,
este logic
adevarata,
(14) ![]() nu este logic
adevarata.
nu este logic
adevarata.
In (13) si (14) avem ![]() si
si ![]() .
.
Pentru (11) vom da demonstratie Beth mai jos. Pentru (13) folosim echivalente astfel:
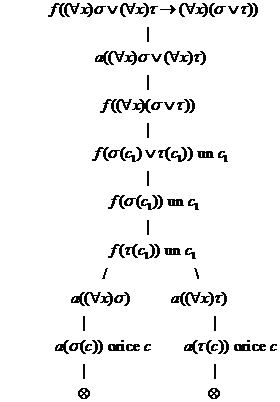
Pentru (13) procedam prin echivalente:
![]()
deoarece
![]() )
)
![]() ( conform lui De Morgan )
( conform lui De Morgan )
![]() (deoarece
(deoarece ![]() )
)
![]() ( conform lui De Morgan )
( conform lui De Morgan )
si ultima formula este logic adevarata conform lui (11).
Pentru (12) consideram doua
predicate binare P si Q , o constanta 1 si formulele
![]() si
si ![]() . Consideram de asemenea o interpretare I in care domeniul este
. Consideram de asemenea o interpretare I in care domeniul este ![]() , interpretarea lui P
este relatia
, interpretarea lui P
este relatia ![]() pe
pe ![]() iar interpretarea lui Q este relatia
iar interpretarea lui Q este relatia ![]() pe
pe ![]() iar interpretarea
constantei este cea uzuala. Interpretarea formulei
iar interpretarea
constantei este cea uzuala. Interpretarea formulei ![]() este
este ![]() iar a formulei
iar a formulei ![]() este
este ![]() . Avem, evident
. Avem, evident ![]() ,
, ![]() astfel ca
astfel ca
![]() .
.
Pentru (14)
consideram un predicat binar P ,
doua constante 0 si 1 si formulele ![]() si
si ![]() . Consideram de asemenea o interpretare I in care domeniul este
. Consideram de asemenea o interpretare I in care domeniul este ![]() , interpretarea lui P
este relatia
, interpretarea lui P
este relatia ![]() pe
pe ![]() iar interpretarea
constantelor este cea uzuala. Interpretarea formulei
iar interpretarea
constantelor este cea uzuala. Interpretarea formulei ![]() este
este ![]() iar interpretarea
formulei
iar interpretarea
formulei ![]() este
este ![]() . Avem, evident,
. Avem, evident, ![]() si
si ![]() astfel ca
astfel ca ![]() .
.
Pe de alta parte daca ![]() si
si ![]() este o fraza
avem:
este o fraza
avem:
(15)
![]() ;
;
(16) ![]() .
.
Pentru (15),
avem ca ![]() este logic
adevarata conform lui (11) si ramane de demonstrat ca
este logic
adevarata conform lui (11) si ramane de demonstrat ca ![]() este logic
adevarata; dam o
demonstratie Beth.
este logic
adevarata; dam o
demonstratie Beth.
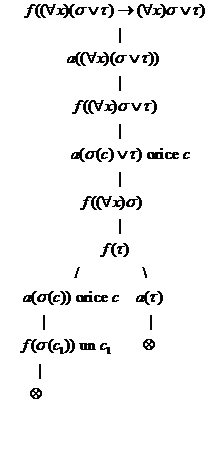
Pentru (16) procedam prin echivalente|
![]()
![]() ( conform lui (14)
( conform lui (14)
![]() .
.
O lista de formule care se pot justifica cu metode asemanatoare cu cele de mai sus este urmatoarea
![]() ( pe scurt
( pe scurt![]() ).
).
![]() ( pe scurt si
( pe scurt si
![]() ).
).
(3) ![]() ( pe scurt
( pe scurt ![]() ).
).
![]() ( pe scurt
( pe scurt ![]() ).
).
(5) ![]() .
.
![]() .
.
(7) ![]() .
.
(8) ![]() .
.
(9)![]() .
.
(10) ![]() .
.
(11) ![]() .
.
(12)![]() .
.
(13) ![]() .
.
(14)![]() .
.
15) ![]() .
.
(16)![]() .
.
(17)![]() .
.
(18) ![]() .
.
(19) ![]() .
.
![]() .
.
(21) ![]() .
.
Copyright © 2026 - Toate drepturile rezervate