LEGI ALE NUMERELOR MARI SI

TEOREMA LIMITA CENTRALA

1. Introducere

Am vazut ca nu putem sti inainte de efectuarea experimentului ce valoare va lua v.a. pe care o studiem. S-ar parea ca, intrucat despre fiecare v.a. dispunem de informatii reduse, cu greu am putea determina comportarea mediei aritmetice a unui numar de v.a. In realitate, in conditii putin restrictive, media aritmetica a unui numar suficient de mare de v.a. isi pierde caracterul intamplator.

Pentru practica este important sa cunoastem conditiile in care actiunea combinata a mai multi factori intamplatori conduce la un rezultat care sa nu depinda de intamplare, deci care sa ne permita sa prevedem desfasurarea fenomenului studiat. Astfel de conditii se dau in teoremele cunoscute sub denumirea comuna de legea numerelor mari.

Teorema limita centrala

Repartitia normala ocupa un loc special printre repartitiile studiate, ceea ce va permite utilizarea ei in anumite conditii in cazul celor mai diferite modele.

Teorema: Fie un sir de variabile aleatoare independente si la fel repartizate cu M(X_n)=m, D(X_n)=s , Y_n=X₁+X₂++X_n. Daca F_n este functia de repartitie a variabilei avem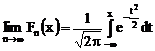

Teorema Liapunov: Fie (X_n)_n un sir de v.a. independente: M(X_n)=m_n,D(X_n)= nIN*. Fie ,

F_n functia de repartitie a variabilei Z_n.

Daca atunci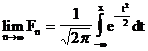

Observatie: Fie (X_n)_n v.a. independente identic repartizate Bernoulli ce iau valorile "1" sau "0" cu probabilitatile "p", respectiv q = "1-p" (M(X_n) = p si D(X_n) = pq)

V.a. Y_n = X₁ + X₂ + + X_n are M(Y_n) = np, D(Y) = npq si

.

=>

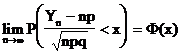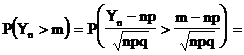
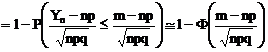
unde F este functia de repartitie a variabilei N(0, 1).

Exemplu: Presupunem ca intr-un sistem de componente legate in paralel, trebuie sa functioneze cel putin "n" componente pentru ca sistemul sa lucreze la performanta maxima. Probabilitatea ca o componenta sa se defecteze este "p". Vrem sa determinam numarul general "m" de componente ce trebuie sa intre in alcatuirea sistemului astfel ca: sistemul sa functioneze la performanta maxima, cu probabilitatea "a a I

Asociem aceasta problema cu "m" incercari independente cu probabilitatea de realizare "p" a unui eveniment. Atunci:

P(numarul de componente defecte m-n) =

Folosind aproximatia ce rezulta din teorema limita centrala obtinem:

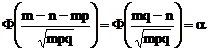si , unde

deci .

3. Inegalitati pentru variabile aleatoare

Teorema:

a)      Fie g :R R functie masurabila satisfacand g(x) b pentru x a unde aIR, bIR

Atunci pentru fiecare v.a. Y,

b)      Fie o v.a.Y si g o functie nenegativa nedescrescatoare g(a)>0 =>

c)      Fie o v.a. X de patrat integrabila si o constanta a > 0 => (inegalitatea lui CEBASEV)

Teorema: Daca X este o v.a. continua ce ia valori pozitive, atunci

, a I

unde M(X), M(X²) sunt valoarea medie, respectiv momentul de ordinul doi.

Exemplu. Departamentul de control al calitatii a verificat 900 de piese la intamplare. Probabilitatea ca o piesa sa se incadreze in standardul existent este 0,9. Fie v.a. X = numarul de piese care se incadreaza in standardul propus din intregul lot. Sa se afle cel mai mic interval simetric fata de m_X in care se afla numarul de piese cu o probabilitate mai mare la 0,99.

Solutie: p = 0,9; X Bi (n; p), n = 900. Din inegalitatea Cebasev

=> e T e 90 deci intervalul este (720

4. Tipuri de convergente pentru siruri de v.a.

Convergenta sirurilor de v.a., spre deosebire de convergenta sirurilor de functii din analiza matematica clasica, are la baza existenta unei masuri de probabilitate pe E.

Vom presupune in cele ce urmeaza ca toate v.a. sunt definite pe acelasi spatiu de probabilitate (E, K, P).

1) Convergenta in probabilitate

Definitie: Sirul de v.a. (X_n)_n converge in probabilitate la v.a. X, daca

.

Teorema

a)      Limita unui sir de v.a. convergent in probabilitate este unica (aproape sigur)

b)      Daca si si a,bR, atunci

c)      Daca    , atunci

2) Convergenta in repartitie

Definitie: Daca sirul de functii de repartitie converge catre o functie de repartitie F, in fiecare punct de continuitate al acesteia, spunem ca sirul de v.a. converge in repartitie catre v.a. X a carei functie de repartitie este F (folosim notatia ).

Teorema:

a)      Daca , atunci

b)      Daca c este o constanta reala si daca , atunci .

3) Convergenta aproape sigura

Definitia 3: Sirul de v.a. converge aproape sigur catre v.a. X (folosim notatia ) daca multimea punctelor e", in care sirul X_n converge punctual, formeaza un eveniment de probabilitate 1:

Acest mod de convergenta este denumit si tare.

Teorema Daca , atunci si implicit

Teorema: Daca X_n, X sunt v.a., atunci urmatoarele afirmatii sunt echivalente

a)      ,

b)      Din orice subsir al sirului (X_n)_n se poate extrage alt subsir asa incat

4) Convergenta in medie

Definitie: Fie (X_n)_n un sir de v.a. si fie X o v.a. Daca exista si M(X^r) si daca spunem ca sirul (X_n)_n converge in medie "r" la X.

Teorema: Convergenta in medie patratica implica convergenta in probabilitate.

5. Legi ale numerelor mari

Teorema lui Bernoulli - forma slaba: Fie A un eveniment a carui probabilitate de realizare este p si fie f_n(A) frecventa relativa de realizare a evenimentului A in n repetari independente ale experimentului in care se produce A.

Atunci pentru fiecare e > 0 are loc egalitatea

Observatie In cazul unei populatii de volum mare, daca se efectueaza o selectie de volum n si se obtin a rezultate favorabile, atunci cu o probabilitate apropiata de unitate, putem afirma ca probabilitatea evenimentului cercetat este data de frecventa relativa.

Prin urmare daca in studiul populatiilor pentru care nu putem determina apriori probabilitatea p, aceasta se poate exprima pe cale experimentala prin frecventa relativa a evenimentului considerat, fapt ce constituie justificarea teoretica a folosirii frecventei relative in loc de probabilitate.

Teorema Cebasev: Fie un sir de v.a. independente doua cate doua, avand dispersiile marginite de aceeasi constanta: D(X_n) C, n = 1, 2,

Atunci, pentru fiecare e > 0,

sau cu alte cuvinte, sirul de v.a. converge in probabilitate catre 0.

Observatii:

a)      Daca M(X₁)=M(X₂)==M(X_n)=m si sunt indeplinite conditiile teoremei Cebasev, atunci

ceea ce explica de ce putem face observatii asupra mediei unei populatii pe baza unei selectii de volum mic comparativ cu al intregii populatii. Explicatia consta in aceea ca selectia implica un numar de masuratori, suficient prin ele insele.

Deci Teorema lui Cebasev sta la baza teoriei selectiei.

b)      Teorema lui Cebasev ne spune ca, desi v.a. independente pot lua valori departe de mediile lor, media aritmetica a unui numar suficient de mare de astfel de v.a. ia, cu o probabilitate foarte mare, valori in vecinatatea constantei

Aceasta observatie ne arata ca intre comportarea fiecarei v.a., si a mediei lor aritmetice exista o mare deosebire, in sensul ca nu putem preciza ce valoare va lua fiecare v.a., insa putem preciza cu o probabilitate apropiata de 1 ce valoare va lua media aritmetica a acestor v.a.

Teorema lui Poisson: Fie A un eveniment a carui probabilitate de realizare variaza pe parcursul unui sir de experimente independente, astfel ca in experimentul de ordin k, P(A)=p_k, k=1,2, si fie f_n(A) frecventa relativa de realizare a lui A in primele n repetari.

Atunci

Teorema Cantelli: Fie X₁,X₂,,X_n, v.a. independente, identic repartizate si . Atunci

Probleme rezolvate

Intr-o institutie publica, consideram v.a. X=varsta unui angajat al institutiei. Se stie ca varsta medie a angajatilor este M(X)=35 cu abaterea medie patratica Sa se gaseasca o limita inferioara a probabilitatii : P(30<X<40). Ce semnifica, din punct de vedere intuitiv, acest lucru ?

Solutie: In momentul in care nu avem informatii suplimentare cu privire la repartitia variabilei aleatoare considerate si se cere o margine inferioara a unei probabilitati de genul celei de mai sus, este necesar sa aplicam inegalitatea Cebasev :

P(|X-M(X)|<)1-D(X)/ . Inainte de toate, vom determina ce valoare va avea .

P(-<X-M(X)<)=P(

Asadar => P(30<X<40)

Intuitiv : exista cel putin 64% sanse ca, alegand la intamplare un angajat, varsta lui sa fie cuprinsa intre 30 si 40 de ani.

Pentru o variabila aleatoare normala P(|X-m|<3)=0,99 Ce valoare se asociaza acestei probabilitati cu inegalitatea Cebasev ?

Solutie : P(|X-m|<3)1-=1-1/9=8/9=0,89

Fie X= numarul de succese pe care le inregistreaza un sportiv in n competitii nationale. Sansa de a obtine un succes este p. X~Bi(n,p). Sa se determine la cate competitii sportive este necesar sa participe si cu ce sansa castiga o competitie oarecare nationala, astfel incat, folosind inegalitatea Cebasev: P(15<X<35)

Solutie: X~Bi(n,p) => M(X)=np; D(X)=np(1-p). Inegalitatea Cebasev se poate scrie: P( P=>

=>np=25 respectiv .

P(15<X<35) => (1-p)=0,8 => p=0,2 => n=125.

Probabilitatea de aparitie a unui eveniment A, intr-o proba, este 0,5. Se poate afirma, cu o probabilitate mai mare de 0,97, ca numarul de realizari ale evenimentului A in 1000 de probe independente va fi intre 400 si 600 ?

Solutie: P(400<K<600) >0,97 P(400-np<K-np<600-np)>0,97 unde n=1000, p=0,5 P(-100<K-M(K)<100)>0,97

Dar P(|K-M(K)|<100)>1-npq/100²=1-1/40=39/40=0,975>0,97 => afirmatia este corecta.

La secretariatul unei Facultati a Universitatii Politehnice Bucuresti, s-a observat ca X = numarul de solicitari,( pe ora), depuse de studenti, este o variabila aleatoare Po(). Sa se determine parametrul, astfel incat, folosind inegalitatea Cebasev, sa calculam P(20<X<40). Sa se gaseasca o margine inferioara a acestei probabilitati.

Solutie: P(|X-|< => P(- <X<

=> si => marginea inferioara este .

O piesa produsa de un robot este considerata buna daca abaterea dimensiunii de control de la valoarea nominala nu depaseste 2 mm. Abaterile aleatoare ale dimensiunii de control de la valoarea nominala sunt repartizate normal cu media 0 si dispersia 3.

a)      Care este proportia de piese bune produse de robot ?

b)      Cate piese trebuie sa se produca pentru ca cel putin una defecta sa se afle printre ele cu o probabilitate mai mare decat 0,95 ?

Solutie:

a)      Fie X variabila aleatoare ce reprezinta abaterea dimensiunii de control de la valoarea nominala:X~N(0,3)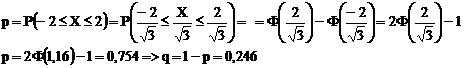

b)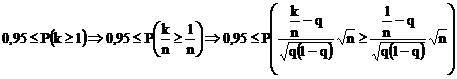     

Un zar cu 10 fete se arunca de 1000 de ori. Doua dintre fete sunt vopsite in rosu si celelalte opt sunt vopsite in albastru. Sa se determine probabilitatea de a se obtine mai mult de 190 de ori o fata vopsita rosie din cele 1000 aruncari.

Solutie : La aruncare avem ca rezultat o fata rosie cu probabilitatea 2/10=0,2 sau o fata albastra cu probabilitatea 8/10=0,8. Fie X_j ~Bi(1 ;0,2). Deoarece experienta s-a repetat de 1000 ori => S_n=~Bi(1000 ; 0,2). Avem

P(X₁+..+X₁₀₀₀>190)=P

Sa se determine o repartitie discreta de 2 variabila aleatoare (X,Y) pentru care cov(X,Y)=0, dar X si Y nu sunt independente.

Solutie: Se considera Y=X² cu repartitia:

M(X)=0, M(Y)=1/2, cov(X,Y)=M(X(X²-1/2))=M(X³)=0

Sa se calculeze P(|X-M(X)|5k) daca X~Bi(20 ;0,5) pentru k=2 si sa se compare rezultatul cu marginea superioara a acestei probabilitati, data de inegalitatea Cebasev.

Solutie : X~Bi(20 ;0,5) => M(X)=np=10, D(X)=np(1-p)=5 ;

Deci P(X=m)=

|X-M(X)|~ ;k sau 3

deci P(|X-M(X)|)=P(|X-10|=5)+ P(|X-10|=6)+ . + P(|X-10|=10)=

P(|X-M(X)|

Folosind inegalitatea Cebasev: P(|X-M(X)| in cazul problemei.

Se considera X₁,X₂, . ,X_k,.. v.a. independente cu P(X_k=a)=.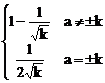

Se poate aplica legea numerelor mari acestui sir de v.a. ?

Solutie: M(X_k)=0 si D(X_k)=M()= Fie v.a. Y_n= avand M(Y_n)==0 si D(Y_n)=

P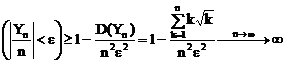 deci nu verifica legea numerelor mari deoarece , conform regulei Cesaro-Stolz,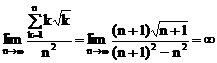

Fie un dispozitiv care are T= timpul de functionare neintrerupta intre 2 defectari succesive ; v.a. T este repartizata exponential Exp(1000). Stiind ca s-au luat in considerare primii 200 de timpi de functionare, sa se calculeze, folosind aproximarea normala, probabilitatea ca timpul total de functionare sa fie mai mare de 201.000 de ore.

Solutie: Fie T_i=timpul de functionare neintrerupta intre defectarea i si i+1,i=0,1,.,199

T₁,T₂, . ,T₂₀₀ v.a. independente, repartizate Exp(1000) cu d.r.: f(x)=,x0 cu =1000 => M(T_i)= si D(T_i)= , i=0,1,.,199

=> M( =200.000, D(

Folosind teorema limita centrala, se obtine aproximatia dorita:

P(>201.000)=P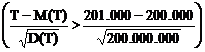P(Z>0,07)=0,5279

Probleme propuse

1.Numarul mediu de avioane, care aterizeaza pe aeroportul din Amsterdam, este de unul la 40 de secunde. Care este probabilitatea ca aproximativ 75 de asemenea zboruri sa se efectueze intr-un interval de 1 ora?

Indicatie: X=numarul de avioane ce aterizeaza sau decoleaza de pe aeroport, X~Po() si se foloseste aproximarea normala prin teorema limita centrala.

Consideram ca s-a aruncat un zar de n=10.000 ori si k=numarul de aparitii ale fetei 6. Aplicati inegalitatea Cebasev pentru a calcula . Calculati o aproximare a aceleasi probabilitati, folosind teorema limita centrala. Ce observati ?

Se considera X₁,X₂, . ,X_k, . v.a. independente cu P(X_k=a)=. Se poate aplica legea numerelor mari acestui sir de v.a. ?

Indicatie: Se calculeaza M(X_k),D(X_k), Y_n=si limita : P

Un zar are 6 fete marcate cu numerele: -14, -4; -2; 2; 4; 14. Fie S_n-suma numerelor obtinute la o aruncare de n ori a zarului. Sa se afle:

a)      b)

Indicatie: Aplicam teorema limita centrala cu M(S_n)=0 si D(S_n)=618n. Se obtin rezultatele:

a)      1; b)     0 .

Fie X~Bi(20;0,3). Folosind aproximatia normala, sa se determine probabilitatea:

a)      P(X3) b) P(36) c) P(X4) d) P(X=4)

Comparati cu valorile obtinute prin calcul direct. Ce observati?

Probabilitatea ca o piesa, aleasa la intamplare sa fie defecta este de 0,1. Intregul lot se respinge daca el contine cel putin 10 piese defecte. Cat de mare este necesar sa fie volumul selectiei, astfel incat, cu o probabilitate 0,6, un lot continant 10% defecte sa fie respins?

Indicatie: P(k)=0,6, aplicam teorema limita centrala si se obtine n100, dar, din considerente de reducere a costurilor de sondaj, se alege n=100 volumul selectiei.

Dintr-o urna care contine bile albe si bile negre in numar egal, se extrag 6 bile cu intoarcere. Se dau 2(5) puncte pentru o bila alba (neagra) si se noteaza v.a. X= suma punctelor obtinute.

a)      Care este repartitia variabilei aleatoare X?

b)      Sa se calculeze P(|X-M(X)|>5) si P(|X-M(X)|>10)

Indicatie: Y=numarul de bile albe extrase => Y~Bi(6; 0,5)

Iar X=2Y+5(6-Y)=30-3Y numarul de puncte castigat la sfarsitul extragerii.

Fie X o variabila aleatoare pentru care M(X)=5, D(X)=4. Se cere sa se calculeze

a)      Valoarea minima pentru P(-1<X<1); b) Valoarea cea mai mare pentru P(|X-5|>6)

c)      Cea mai mare valoare pentru P(|X-5|>4); d) Cea mai mica valoare pentru P(|X-5|

e)      Valoarea lui k, pentru care P(|X-5|<k)0,84

Folosind aproximarea normala pentru sirul de variabile aleatoare independente

X₁ ,X₂.,X₁₀₀ , sa se determine P(|S₁₀₀ -M( S₁₀₀ )|<3) daca S₁₀₀= si

a)      X~Bi(n,p) unde n=10, p=0,2 ; b) X~Po() unde =2 ; c)X~Geom(p) unde p=0,4

d)      X~N(m,) unde m=3, =2; e) X~Exp() unde =3( f(x)=,x>0)