Integrarea prin metode numerice

Integrarea prin metode numerice

Consideratii teoretice

Exista mai multe definitii ale notiunii de "integrala" fiecare definitie avand propriul suport tehnic. In mod intuitiv, integrala unei functii continue, pozitive, f(x), de variabila reala si luand valori reale, intre doua puncte a si b, reprezinta valoarea ariei marginite de segmentele x = a, x = b, axa x si graficul functiei f(x), asa cum este prezentat in figura 1.

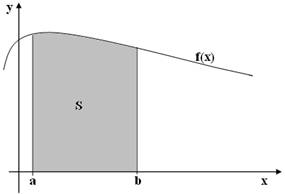
Figura 1. Integrala definita ca aria de sub graficul unei functii

Marimea suprafetei S este data de integrala functiei f(x) intre a si b:

In calculele ingineresti se intalnesc numeroase situatii in care este necesara rezolvarea integralelor definite (ex. determinarea modelului matematic pentru diverse tipuri de reactoare, determinarea concentratiei fractiunilor la distilarea simpla etc.).

Integralele prezentate in cursurile obisnuite de analiza matematica sunt alese intentionat pentru simplitatea lor, in scopuri didactice; cele gasite in aplicatiile reale sunt adesea mult mai complicate. Unele integrale nu pot fi calculate exact, altele necesita functii speciale care sunt la randul lor dificil de calculat, iar altele sunt atat de complicate incat fie nu pot fi rezolvate analitic, fie rezolvarea lor necesita un volum foarte mare de munca si de timp. Pentru rezolvarea integralelor complexe intr-un mod cat mai eficient (cat mai simplu si intr-un timp cat mai scurt) au fost elaborate numeroase metode de aproximare a integralelor. Una dintre metodele cele mai populare si mai frecvent folosite este metoda grafica.

Metoda grafica presupune trasarea pe hartie milimetrica a functiei f(x), reprezentarea intervalului pe care se face integrarea (punctele x = a si x = b) urmata de planimetrarea suprafetei marginite de axa x, de curba descrisa de functia f(x) si de paralelele la ordonata corespunzatoarea punctelor a si b. Acest procedeu este destul de laborios, necesitand multa atentie si acuratete grafica. Cu toate acestea, metoda este in continuare folosita ca instrument in rezolvarea integralelor definite aparute in problemele de inginerie.

O alta categorie de metode de aproximare a integralelor definite sunt metodele numerice. Metodele numerice pot fi mai simple sau mai complexe, in functie de precizia cu care trebuie calculata integrala. Cu cat precizia este mai buna, cu atat metoda este mai complexa, iar volumul de munca mai mare. Dezvoltarea tehnicii de calcul a facut si face ca aceste metode sa fie din ce in ce mai abordabile,    reducand considerabil atat volumul de munca cat si timpul de lucru. Cele mai populare metode de intregrare numerica sunt: metoda dreptunghiului, metoda trapezului, regula Simpson.

Metoda trapezului

Consideram ca functia de integrat este f(x). Aceasta functie poate fi aproximata cu o functie polinomiala de ordin n, astfel incat:

f(x)dx = f'(x)dx = c₀ + c₁x + c₂x² + c₃x³ + + c_n-1x^n-1 + c_nxⁿ

Metoda trapezului presupune ca n = 1, aproximand functia de integrat cu o dreapta, iar suprafata de sub curba corespunzatoare functiei de integrat cu suprafata unui trapez (figura 2).

f(x)dx = f'(x)dx = c₀ + c₁x

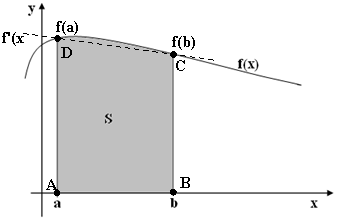
Figura 2. Integrarea cu ajutorul regulii trapezului

Pentru calculul integralei se foloseste relatia:

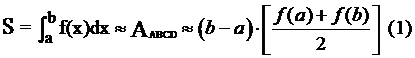
sau, altfel scris:

Metoda trapezului pe segmente multiple

Metoda trapezului pe segmente multiple presupune segmentarea suprafetei de sub curba corespunzatoare functiei si aplicarea metodei trapezului pentru fiecare segment in parte (figura 3). Suma rezultatelor obtinute pentru fiecare segment este aproximativ egala cu valoarea integralei. Volumul de munca este putin mai mare, insa precizia este mult mai buna.

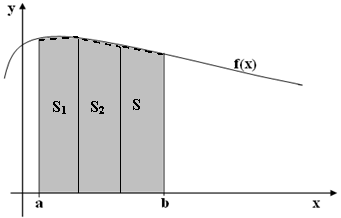
Figura 3 Regula trapezului pe segmente multiple

Daca intervalul (b-a) este impartit in n segmente egale, lungimea fiecarui segment este:

iar integrala poate fi scrisa ca suma a h integrale. Relatia de calcul a integralei devenind:

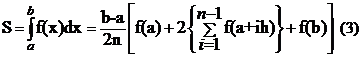
Obs. Cu cat n este mai mare, cu atat precizia este mai buna.

Regula Simpson

Aceasta metoda de integrare mai este cunoscuta si ca "regula Simson 1/3". Daca in cazul metodei trapezului functia de integrat era aproximata cu o functie polinomiala de ordinul 1, in cazul regulii Simpson functia de integrat este aproximata cu o polinomiala de ordinul 2.

f(x)dx = f'(x)dx = c₀ + c₁x + c₂x²

Formula de calcul a integralei este:

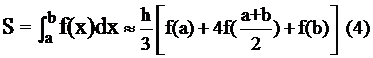
in care,

Aplicatii:

Pentru calculul volumului unui reactor ideal cu deplasare necesar prelucrarii unui amestec gazos format din componentii A si B, pana la un grad de transformare al reactantului A de 50% este necesara determinarea valorii timpului spatial, ceea ce presupune rezolvarea urmatoarei integrale:

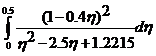
Sa se rezolve integrala folosind metoda grafica si    cele trei metode numerice.

Mod de lucru pentru metoda trapezului:

1. Se definesc limitele de integrare "a" si "b";
2. Se calculeaza valoarea functiei in punctele "a" si "b"
3. Se calculeaza integrala cu formula data de relatia 2.

Mod de lucu pentru metoda segmentelor multiple:

1. Se definesc numarul de segmente "n si limitele de integrare "a" si "b".
2. Se calculeaza pasul de integrare "h"
3. Se calculeaza functia in punctele "a" si "b"
4. Se creeaza o coloana "i" in care se incriu valori de la 1 la 10.000
5. Se calculeaza valoarea punctului "a+i·h" din formula 3
6. Se calculeaza functia in punctul "a+i·h", utilizand formula functiei din integrala data
7. Se determina integrala cu formula data de relatia 3.

Mod de lucru pentru metoda Simpson:

1. Se definesc limitele de ingrare, "a" si "b" si pasul de integrare "h"
2. Se calculeaza valoarea functiei in punctele "a" si "b"
3. Se determina punctul "(a+b)/2" si apoi se calculeaza valoarea functiei in punctul respectiv.
4. Se calculeaza integrala cu ajutorul formulei din relatia 4

Distanta (in metri) pe care se deplaseaza o racheta in intervalul de timp t₁ = 8 s, t₂ = 30 s, poate fi calculata cu relatia:

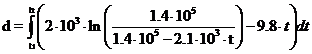
Calculati aceasta distanta folosind metodele numerice prezentate anterior.

Bibliografie

1. A. Kaw, M. Keteltas, Trapezoidal rule, https://numericalmethods.eng.usf.edu

2. A. Kaw, M. Keteltas, Simpson's 1/3 rule, https://numericalmethods.eng.usf.edu

3. I. Mamaliga, S. Petrescu, Operatii de transfer de masa, vol. I., Ed. Cermi, Iasi, 2004

4. O. Muntean, A. Woinaroschy, G. Bogza, Aplicatii la calculul reactoarelor chimice, Ed. Tehnica, Bucuresti, 1984