 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
FUNCTII TRIGONOMETRICE ALE ARCULUI DUBLU
Vom deduce valorile sin2x, cos2x, tg2x, apoi ca aplicatie valorile sin3x, cos3x.
sin2x =
2sinx cosx , ( ) x I R
Avem
urmatoarele formule:
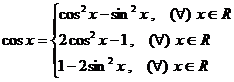
![]() a.i. cosx 0, cos2x
a.i. cosx 0, cos2x
Demonstratie
sin2x = sin(x+x) = sinx cosx + sinx cosx = 2sinx cosx
(am aplicat formula sin(a b) = sina cosb + sinb cosa, inlocuind a b = x )
cos2x = cos(x+x) = cosx cosx - sinx sinx = cos2x - sin2x
(am aplicat formula cos(a b) = cosa cosb - sinb sina, inlocuind a b = x )
cos2x = cos2x - sin2x = cos2x - (1-cos2x) = 2 cos2x -1 sau
cos2x = cos2x - sin2x = 1 - sin2x - sin2x = 1 - 2 sin2x
tg2x = tg(x+x) = ![]()
(am aplicat formula tg(a b) = ![]() )
)
Aplicatii
sin3x = sinx (3 - 4sin2x) , ( ) x I R cos3x = cosx (4cos2x - 3) , ( ) x I R
Vom deduce prima formula, pentru cea de-a doua procedandu-se analog.
sin3x = sin(2x+x) = sin2x cosx + sinx cos2x = 2sinx cos2x + sinx(1 - 2sin2x) = 2sinx (1 - sin2x) + sinx - 2sin3x = 3sinx - 4sin3x = sinx (3 - 4sin2x).
Din formula cos2x = 1 - 2sin2x,
deducem ![]() , ( ) x I R,
, ( ) x I R,
iar din formula cos 2x = 2cos2x
- 1, decucem ![]() , ( ) x I R.
, ( ) x I R.
Aceste doua ultime formule se mai numesc formule de liniarizare si ele sunt utile in aplicatii intrucat permit trecerea de la patrate de functii trigonometrice la functii trigonometrice la puterea intai, insa avand argumentul dublu.
In multe aplicatii sunt utile si formulele:
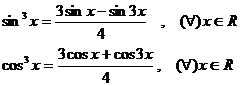 care sunt deduse
imediat din formullele ce exprima sin3x, respectiv cos3x.
care sunt deduse
imediat din formullele ce exprima sin3x, respectiv cos3x.
2. Probleme rezolvate
1) Demonstrati identitatile trigonometrice:
a)
(cos a + cos b)2 +
(sin a + sin b)2 = 4![]() c)
(cos a - cos b)2 + (sin a - sin b)2 = 4
c)
(cos a - cos b)2 + (sin a - sin b)2 = 4![]()
b) (cos a + cos 2a) (2cos a - 1) = cos 3a + 1
Rezolvare
Vom verifica b), a) si c) verificandu-se analog.
(cos a - cos b)2 + (sin a - sin b)2 = cos2a + cos2b - 2cos a cos b + sin2a + sin2b - 2sin a sin b =
= 2 - 2(cos a cos b + sina sin b) =
2 - 2cos(a-b) = 2[1 - cos(a-b)] = 4![]()
2) Demonstrati ca: ![]()
Rezolvare
Folosim formula ![]()
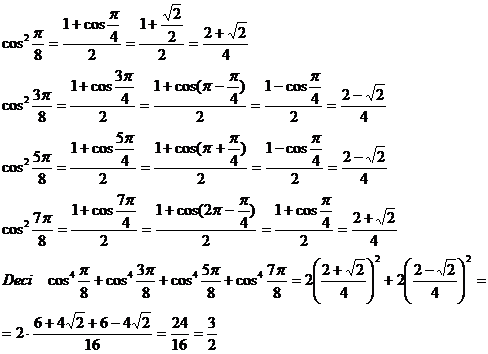
3) Sa se arate ca:
cos60 cos660 cos420 cos780 = ![]() , demonstrand mai intai 4 cos a cos(600 - a cos(600 + a) = cos 3a
, demonstrand mai intai 4 cos a cos(600 - a cos(600 + a) = cos 3a
Rezolvare :
cos a cos(600 - a cos(600 + a cos a (cos600 cos a + sin600 sin a ( cos600 cos a - sin600 sin a
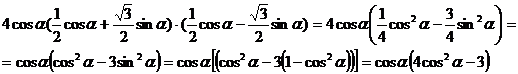
In identitatea verificata inlocuim a = 60 si a = 180 si obtinem:
4cos60 cos540 cos660 = cos180 4cos180 cos420 cos780 = cos540
Inmultind membru cu membru cele doua egalitati obtinem rezultatul dorit.
4) Demonstrati ca ![]()
Rezolvare:
![]()
Impartim prin
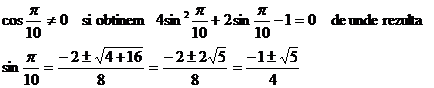
Evident alegem numai solutia
pozitiva, intrucat ![]()
5) Demonstrati identitatea: 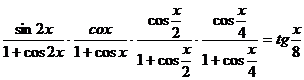
Rezolvare:
Membrul stang se scrie astfel:
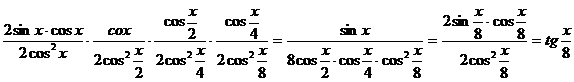
7) Calculati valoarea produsului P = cosx cos2x cos22x . .cos2nx.
Rezolvare:
Calculam
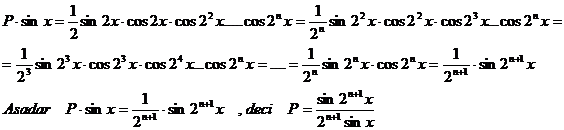
Observatie
Retineti modalitatea de calcul a acestui produs de cosinusuri in care argumentele formeaza o progresie geometrica. Pentru calculul sau, a fost necesar un "bobarnac" acesta fiind sinx, cu care am inmultit egalitatea, factorii din membrul drept "consumandu-se" doi cate doi pe baza formulei
sin a cosa= ![]() sin2a
sin2a
8) a) Demonstrati identitatea trigonometrica ![]()
b) Deduceti valoarea produsului: ![]()
Rezolvare: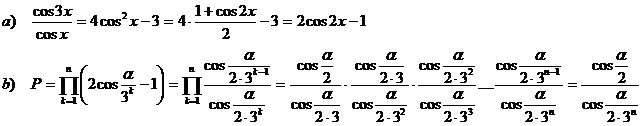
3. Probleme propuse
1) Demonstrati identitatile trigonometrice:
a) sin 6x = 2sin 5x cosx - sin 4x c)
![]()
b) cos 6x = 2cos 5x cos x - cos 4x
2) Sa se arate ca:
a) ![]() e)
sin(a + b) sin c + sin(b - c) sin a = sin(a + c) sin b
e)
sin(a + b) sin c + sin(b - c) sin a = sin(a + c) sin b
b) cos2 (x + y) - cos2(x - y) + sin 2x sin 2y = 0 f) sin(a + b) cos c - cos(b - c) sin a = cos(a + c) sin b
c) [sin2(x + y) + sin2(x - y)] [cos2(x + y) + cos2(x - y)] = 1 - cos2 2x cos2 2y
d) (1 + tgx)2 + (1 + ctgx)2
= 4 ![]() g)
(sin 2a + sin 4a)2 + (cos 2a
+ cos 4a)2 = 4 cos2
a
g)
(sin 2a + sin 4a)2 + (cos 2a
+ cos 4a)2 = 4 cos2
a
3) Demonstrati identitatile:
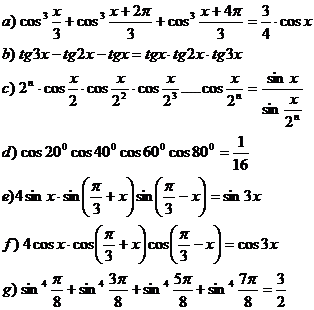
4) Demonstrati ca:
a) cos2 2x + cos2 (x - y) - 2 cos(x - y) cos(x + y) cos 2x = sin2 x + sin2 y + 2sin x sin y cos(x + y) , ( ) x, y I R
b) cos x < ![]() , ( ) x I p
, ( ) x I p
c) sin(x + y) sin(y + z) sin(z
+ x) sin 2x sin 2y sin 2z, ( ) x,
y, z, I [0, ![]() ]
]
5) Calculati: ![]()
6) Calculati produsul: ![]()
Functiile trigonometrice sin, cos, tg, ctg se exprima rational in functie de tangenta semiunghiului dupa urmatoarele formule:
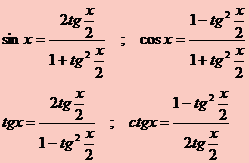 , cos
, cos![]()
Demonstram primele doua egalitati:
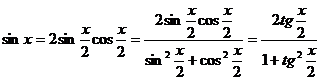
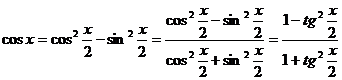
Probleme rezolvate
1) Determinati imaginea functiei f : R R, f(x) = a sin x + b cos x ; a, b I R.
R. Notam ![]() si atunci
functia f in variabila t este f(t) =
si atunci
functia f in variabila t este f(t) = ![]() .
.
Notam f(t) = y si obtinem 2at + b - bt2 = y + y t2 sau (b+y) t2 - 2at - b + y = 0, care este o ecuatie de gradul al doilea in variabila t. Intrucat t I R se impune conditia D ≥ 0 sau 4a2 - 4(y2 - b2) ≥ 0.
Deci ![]()
2) Daca tg a = 2, calculati sin 4a si cos 4a
R. Calculam ![]() si
si
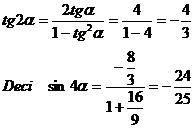
Analog pentru cos 4a
5. Transformarea sumei (diferentei) de functii trigonometrice in produs.
Au loc urmatoarele identitati:
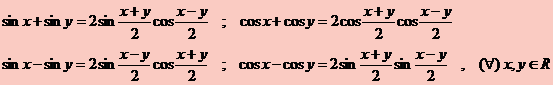
Demonstratie:
sin(a+b) = sin a cos b + sin b cos a sin(a-b) = sin a cos b - sin b cos a
Notam a+b = x ; a-b = y ,
rezulta ![]() .
.
Adunam primele egalitati
membru cu membru si obtinem: ![]()
Pentru y -y rezulta, tinand cont de imparitatea sinusului: ![]()
Pentru celelalte doua identitati folosim:
cos(a+b) = cos a cos b - sin a sin b cos(a-b) = cos a cos b + sin a sin b
si cu aceleasi notatii, adunand si scazand egalitatile membru cu membru obtinem rezultatele anuntate.
Observatie
Deduceti formulele:
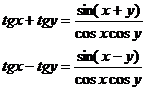
6. Transformarea produselor de functii trigonometrice in sume.
Au loc urmatoarele identitati:
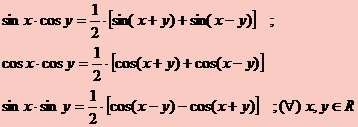
Folosind formulele deduse anterior si calculand membrul drept, sau folosind formulele ce dau functiile trigonometrice ale sumei sau diferentei (tot calcul in membrul drept) obtinem rezultatele anuntate.
1) Calculati ![]()
R. 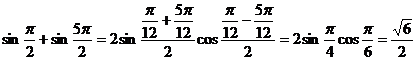
2) Demonstrati identitatile:
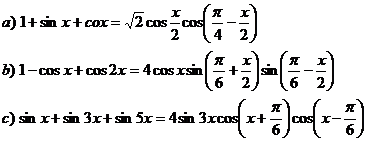
Rezolvare
a) 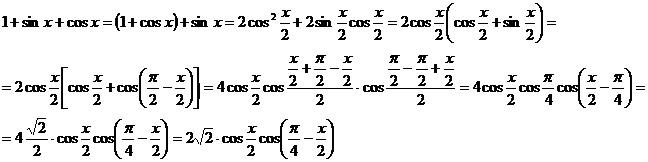
b) 
c) 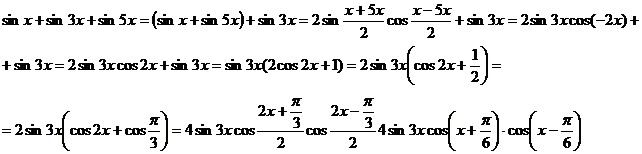
3) Simplificati fractiile:
![]() ;
; ![]()
R. ![]()
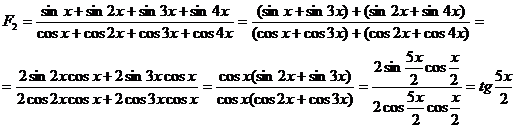
4) Demonstrati ca:
a) ![]() , ( ) x, y I p b)
, ( ) x, y I p b) ![]() ( ) x, y I p
( ) x, y I p
Rezolvare
a) Inegalitatea propusa este echivalenta cu
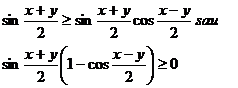 , ambii factori fiind pozitivi, deci inegalitatea se
verifica.
, ambii factori fiind pozitivi, deci inegalitatea se
verifica.
Analog se verifica si cea de-a doua.
Aceste inegalitati sunt de tip Jensen pentru functiile sinus si cosinus, restrictionate la [0,p], respectiv [0, p
5) Demonstrati ca:
![]()
![]()
"n" radicali ( ) n I N*
R. Notam ![]() , n IN*
, n IN*
x1=1
Demonstram prin inductie ca
P(n) : xn = ![]() , n I N*
, n I N*
Observam ca ![]() , ( ) n I N, n ≥ 2.
, ( ) n I N, n ≥ 2.
P(1) este o propozitie adevarata.
Presupunem P(k) adevarata ( ![]() ) si demonstram ca P(k+1) este
adevarata, deci ca
) si demonstram ca P(k+1) este
adevarata, deci ca
![]() . Dar
. Dar ![]()
Tinand cont ca xk >
0, obtinem ![]() , deci P(k+1) este adevarata.
, deci P(k+1) este adevarata.
6) Calculati urmatoarele sume:
a)
S1 = sin x + sin 2x
+ . .+ sin nx; c) S3 = ![]()
b) S2 = cos x + cos 2x + . .+ cos nx;
Rezolvare
Observam in cazul primelor doua sume ca argumentele functiilor trigonometrice (sinus si cosinus) formeaza o progresie aritmetica de ratie r = x.
Pentru a le calcula, inmultim ambii
membri cu ![]() (in general cu
(in general cu ![]() ).
).
Calculam S1, pentru ca S2 se calculeaza in mod asemanator.
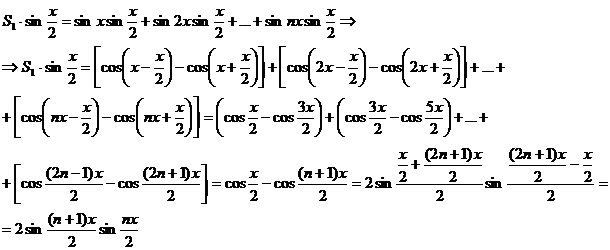
c) Vom demonstra mai intai identitatea: ![]() (*)
(*)
Membrul drept se scrie succesiv :
![]()
Conform (*), S3 = (ctg x - ctg 2x) + (ctg 2x - ctg22x) + . ..+(ctg2n-1x - ctg2nx) = ctg x -ctg2nx.
7) demonstrati ca daca a + b+ c = ![]() , atunci
, atunci ![]()
Rezolvare
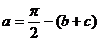 , deci sin a = cos(b+c) si inegalitatea se scrie:
, deci sin a = cos(b+c) si inegalitatea se scrie:
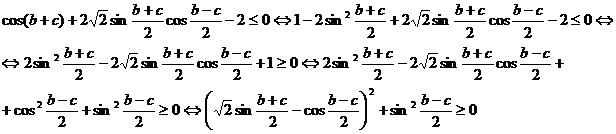
care este evidenta.
8.Probleme propuse
1) Calculati, scriind rezultatul sub forma de produs: a) sin 1050 + sin 750;
b) cos 750 + cos 150.
2) Verificati identitatile:
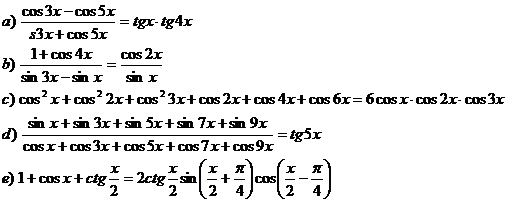
3) Sa se precizeze semnul numerelor:
a)
sin 5 + sin 4; b)
cos 2 + cos 4; c) ![]()
a) Daca x = y+z, sa se arate ca: tg x + ctg y + ctg z = tgx ctgy ctgz
b) Daca x+y+z = p, sa se arate ca: tg x + tg y + tg z = tg x tg y tgz
c) Daca x+y+z= 2p , sa se arate ca: sin x + sin y + sin z = 4![]()
5) Demonstrati ca:
1-cos2x - cos2y - cos2z
+ 2cosx cosy cosz = 4![]()
) x, y, z I R.
6) Calculati produsul: ![]()
7) Calculati urmatoarele sume:
a) S1= ![]() b) S2
= cos x + cos 3x + cos 5x + . .+cos(2n-1)x.
b) S2
= cos x + cos 3x + cos 5x + . .+cos(2n-1)x.
8) Demonstrati identitatile:
a) ![]() b) sin200 sin400 sin600 sin800 =
b) sin200 sin400 sin600 sin800 = ![]()
Solutii probleme2.3
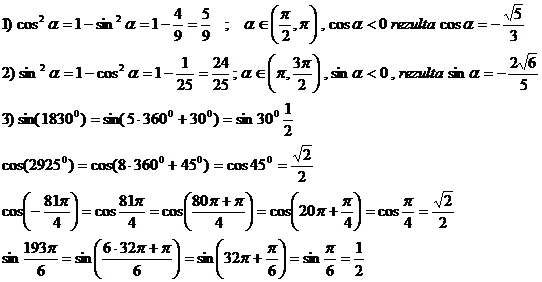
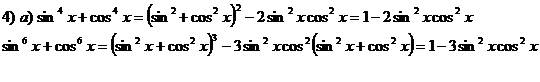
Expresia devine ![]()
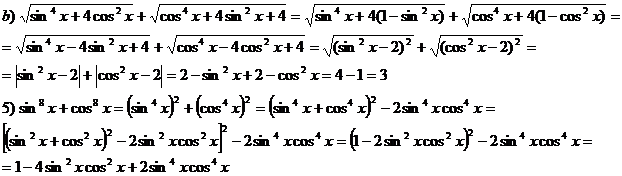
Inegalitatea de demonsrat este:
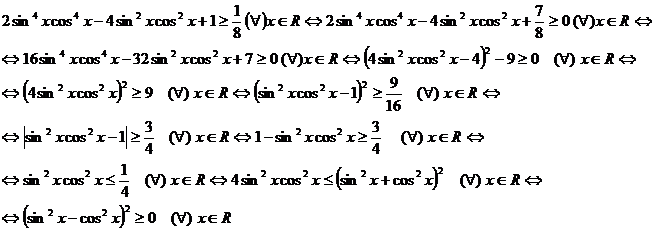
care este adevarata.
Solutii probleme propuse2.5
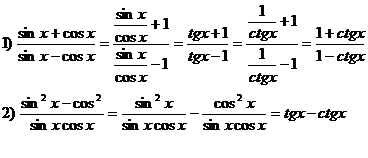
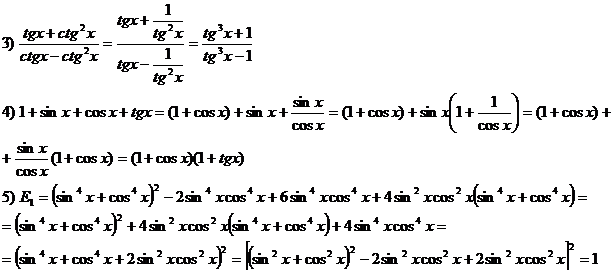
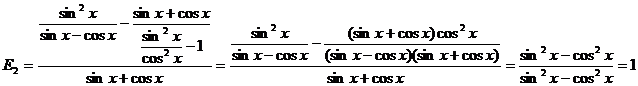
Solutii probleme propuse2.8
1) a) Expresia este egala cu ![]()
b) Expresia devine: ![]() , etc .
, etc .
2) Membrul stang al egalitatii este:
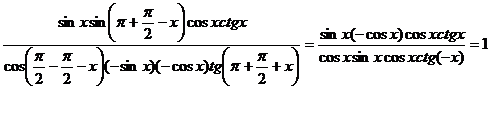
3) a) tg10 tg890= tg10 ctg10 = 1 => tg20 tg880 = tg20 ctg20 = 1 => tg440 tg460 = tg440 tg440 = 1 => tg450 = 1
b) Membrul stang este: 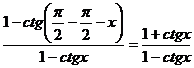 , iar membrul drept
este:
, iar membrul drept
este:
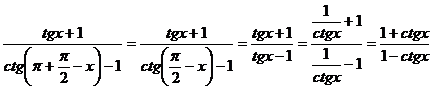
Solutii probleme propuse3.3
1) sin150 = sin(450 -
300) = sin450 cos300
- sin300 cos450
= ![]() , analog celelalte.
, analog celelalte.
2) sin1050 = sin(900 + 150) = cos(900 - 900 - 150) = cos150, etc .
3) a) sin(a+b) sin(a-b)= (sina cosb + sinb cosa)(sina cosb - sinb cosa)= sin2a cos2b - sin2b cos2a = =sin2a(1-sin2b) - sin2b(1-sin2a) = sin2a - sin2a sin2b - sin2b + sin2a sin2b = sin2a - sin2b
b) Analog cu a)
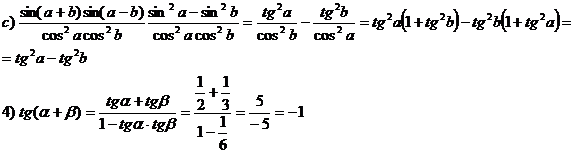
a b este in cadranul II, deci a b = ![]()
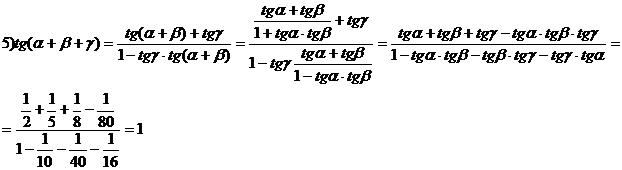
a b g sunt in cadranul I si toate mai mici decat p/4 (justificati)
Deoarece tg(a b g) > 0, rezulta ca a b g I p/2) sau a b g I p p/2), ultima incadrare nefiind posibila. Ramane a b g p
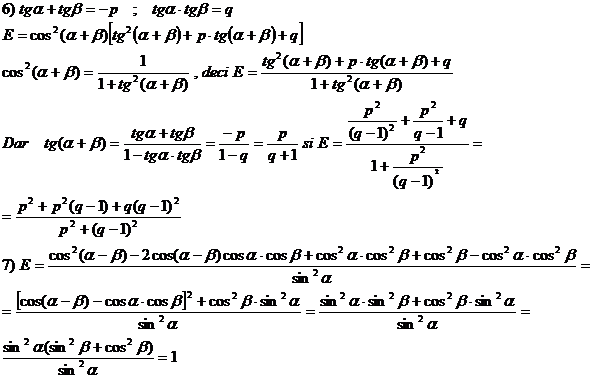
8) Membrul drept al egalitatii se scrie succesiv:
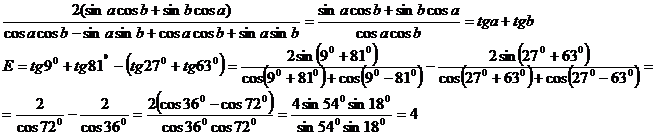
(In demonstratie am folosit ![]() , care se prezinta mai tarziu, dar care se poate deduce
si cu formulele utilizate pana la acest moment)
, care se prezinta mai tarziu, dar care se poate deduce
si cu formulele utilizate pana la acest moment)
9) cosx sin(y-z) = cox(siny cosz - sinz cosy) = cosx siny cosz - cosx sinz cosy
cosy sin(z-x) = cosy sinz cosx - cosy sinx cosz
cosz sin(x-y) = coz sinx cosy - cosz siny cosx Prin adunare se obtine 0.
a) Membrul stang este: ![]()
b) Membrul stang este:
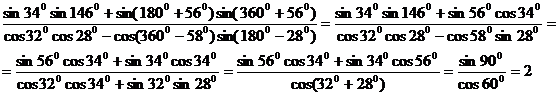
c) Membrul stang este: 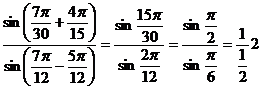
d) Membrul stang este:
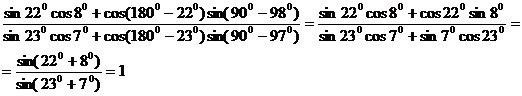
11) Se poate folosi ![]() si gasim
si gasim
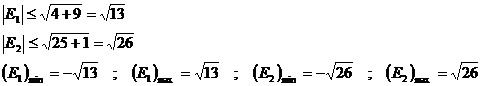
Solutii probleme propuse3
1) a) sin 6x = 2sin 5x cos x - sin 4x sin(5x + x) = 2sin 5x cos x - sin 4x sin 5x cosx + sinx cos 5x - 2sin 5x cos x = -sin 4x sin 5x cos x = sin x cos 5x + sin 4x sin 5x cos x - sin x cos 5x =
= sin 4x sin(5x - x) = sin 4x, evident.
b) Analog cu a).
c) Membrul stang se scrie succesiv:
![]()
2) a)
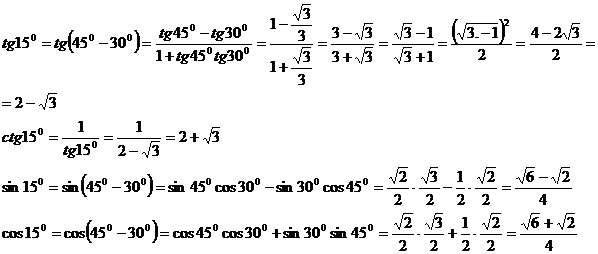
Membrul stang va fi: 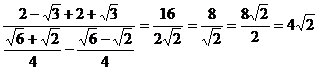
b) cos2(x + y) - cos2(x - y) + sin 2x sin 2y=
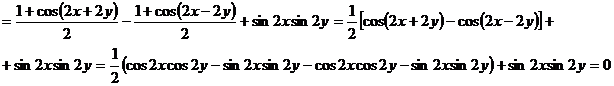
c) Membrul stang este:
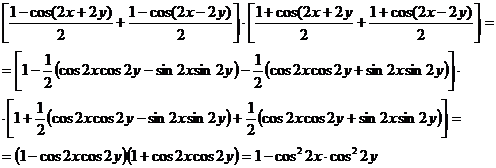
d) 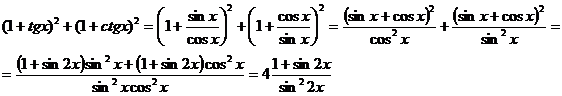
e) sin(a + b) sin c + sin(b - c) sin a = sin a cos b sin c +sin b cos a sin c + sin b cos c sin a - sin c cos b sin a = sin b(sin a cos c + sin c cos a) = sin b sin (a+c).
f) Analog ca e)
g) (sin 2a + sin 4a)2 + (cos 2a + cos 4a)2 = sin2 2a + cos2 2a + sin2 4a + cos2 4a + 2(sin 4a.sin 2a + cos 4a cos 2a) = 2 + 2cos(4a - 2a) = 2 + 2cos 2a = 2(1+cos 2a) = 4 cos2 a.
3) a)
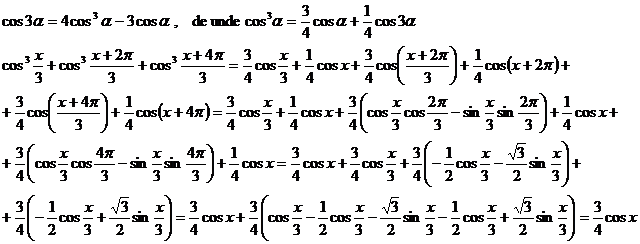
b)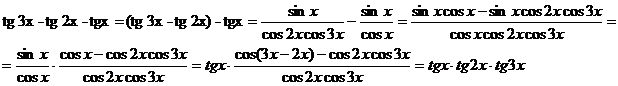
c) Vezi exercitiul rezolvat nr. 7
d) P = cos 200 cos 400 cos 600 cos 800
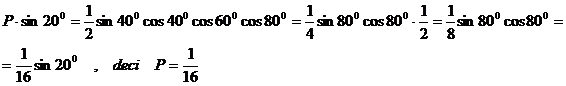
e) , f) se fac calcule in membrul stang.
g)
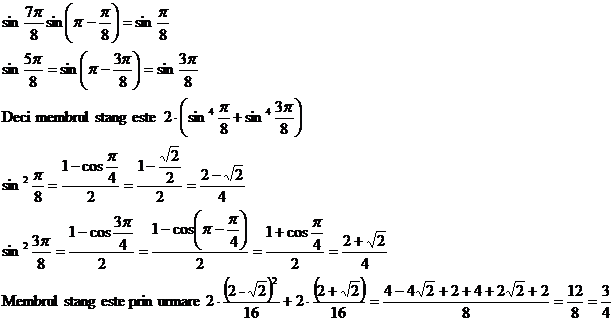
4) a) Membrul stang se scrie astfel:
cos2 2x -2cos 2x cos(x-y) cos(x+y) + cos2 (x-y) cos2(x+y) + cos2 (x-y) - cos2 (x-y) cos2(x+y)=
[cos2x - cos(x-y) cos(x+y)]2 + cos2 (x-y) sin2(x+y) = [cos 2x - (cos x cos y + sin x siny) (cos x cosy - sin x sin y)]2 + cos2(x-y) sin2(x+y)= (cos 2x - cos2 x cos2 y + sin2 x sin2 y)2+ cos2(x-y) sin2(x+y)= (cos2 x - cos2x cos2y + sin2x sin2y - sin2 x)2+ cos2(x-y) sin2 (x+y) = (cos2 x sin2y -
- sin2 x cos2 y)2 + cos2 (x-y) sin2 (x+y) = (sin x cos y - sin y cos x)2 (sin x cos y + sin y cos x)2+
+ cos2(x-y) sin2(x+y) = sin2 (x-y) sin2 (x+y) + cos2 (x-y) sin2 (x+y) = sin2 (x+y).
Membrul drept este:
sin2 x + 2sin x sin y cos (x+y) + sin2 y cos2 (x+y) - sin2 y cos2 (x+y) + sin2 y =
= [sin x + sin y cos(x+y)]2 + sin2 y sin2 (x+y) = (sin x + sin y cos y - sin2 y sin x)2 + sin2y sin2(x+y)= (sin x cos2 y + sin y cos x cos y)2 + sin2 y sin2 (x+y) = cos2 z(sin x cos y
+ sin y cos x)2 + sin2 y sin2 (x+y) = cos2 y sin2 (x+y) + sin2 y sin2 (x+y) = sin2 (x+y).
b) Inegalitatea este echivalenta cu:
![]() care este
adevarata in conditiile problemei
care este
adevarata in conditiile problemei ![]()
5) Vezi exercitiul rezolvat nr. 4
6) ![]() , api se procedeaza ca la exercitiul rezolvat nr.
6. Se gaseste
, api se procedeaza ca la exercitiul rezolvat nr.
6. Se gaseste 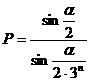
Solutii probleme propuse8
1) a) sin1050 + sin750
= ![]()
b) Analog a)
2) a) ![]()
b) ![]()
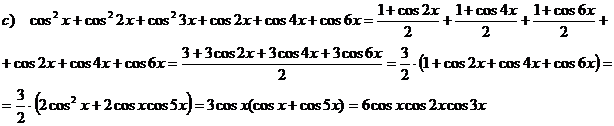
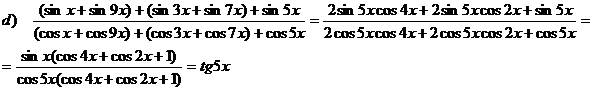
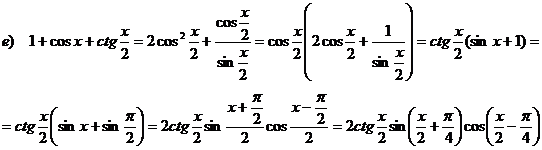
3)![]()
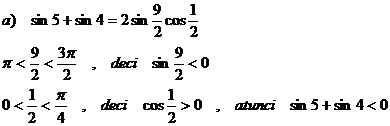
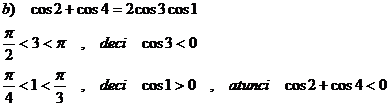
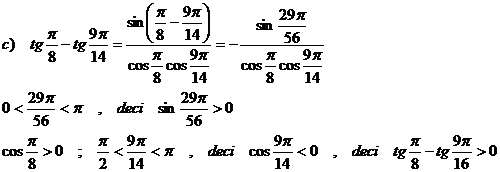
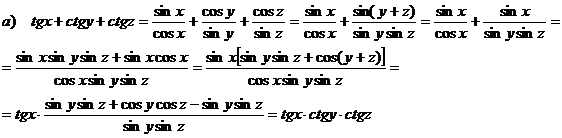
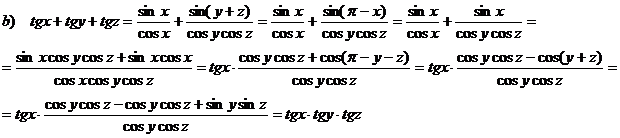
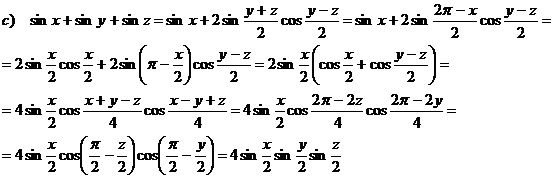
5) Membrul stang este: ![]()
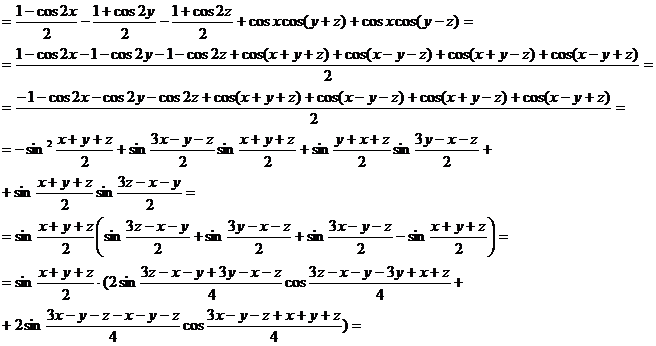
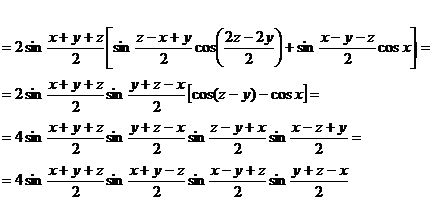
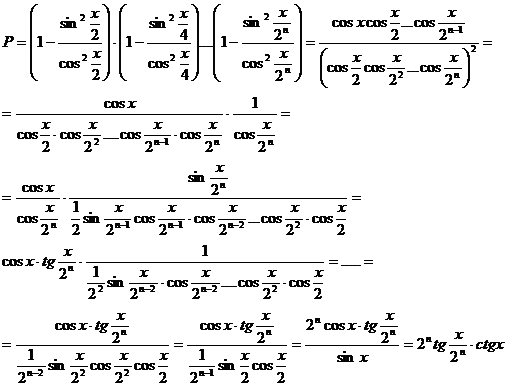
7) a) Se cauta o descompunere a termenului general de tipul f(k) - f(k+1).
In acest sens, verificam identitatea: ![]()
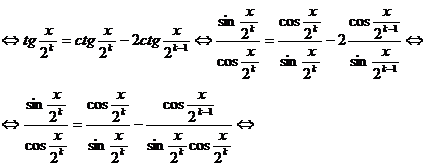
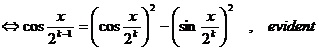 sumand egalitatea, obtinem :
sumand egalitatea, obtinem : ![]()
b) Vezi exercitiul rezolvat nr. 6)
a) Se poate aplica metoda de la 7 b), adica se poate inmulti
egalitatea cu ![]() , etc . .
, etc . .
b) P = sin200 sin400 sin600 sin800 =
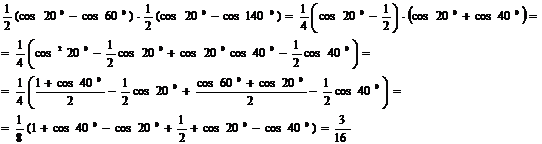
Copyright © 2025 - Toate drepturile rezervate