Comparatii legate de timpul de viata

Asigurari de persoane. Timp de viata

Cel mai simplu model de asigurari de persoane este de urmatorul tip:

Un individ (asiguratul, notat cu A) incheie cu o societate de asigurari (asiguratorul, notat cu S) urmatorul contract:

A se obliga sa plateasca lui S o suma de bani a(t) la fiecare moment de timp t (masurat in ani, luni, saptamini) pina la un moment , m > 0. Incepind de la acest moment, S se obliga sa plateasca lui A o alta suma de bani s(t) pina la sfirsitul vietii lui A.

De exemplu A este un salariat iar S este o casa de pensii. Pina la pensionare, A plateste o suma la fiecare unitate de timp (de exemplu luna sau chenzina) iar dupa aceea S se obliga sa ii plateasca o pensie in caloare de s(t) lei. In cazul cel mai simplu m este o constanta (de exemplu m = 35 de ani = 420 luni = 840 chenzine).

Suma platita de A este

S_A = a₀ + a₂ + . + a_m

Iar cea platita de S este

S_S = s₀ + s₁ + .+ s_{T - m}

unde T = T_A este timpul pe care il mai are de trait A din momentul inceperii asigurarii.

Perechea de functii (a,s) se numeste plan de asigurare pe viata, sau plan de pensie iar variabila aleatoare T se numeste timpul de viata (al asiguratului)

Conditia ca planul sa fie echitabil este ca

S_A = S_S

Apar doua probleme.

Prima este ca T este o variabila aleatoare. S nu are de unde sa stie cit timp va trai A. Dar, putem presupune ca in urma unor investigatii statistice de durata, S cunoaste repartitia lui T.

A doua problema este ca o unitate monetara la momentul t₀ nu este egala cu aceeasi unitate monetara la un moment ulterior , t₁ .

Sa neglijam deocamdata a doua problema.

Inseamna ca un contract echitabil in sensul satisfacerii ecuatiei (1.3) nu este posibil. O varianta de a-l inlocui, in caz ca S are multi asigurati cu aceeasi repartitie ca a lui A este de a inlocui egalitatea (1.3) cu

S_A =ES_S

Dar S_A este de asemenea o variabila aleatoare. Motivul este ca este posibil ca asiguratul A sa moara inaintea momentului m. Asa ca (1.1) ar trebui inlocuita cu

S_A = a₀ + a₂ + . + a_{m T}

iar (1.2) cu

S_S = (s₀ + s₁ + .+ s_{T - m})1_{(T m)}

Acum conditia ca planul sa fie echitabil devine

ES_A = ES_S

Luam acum in calcul valoarea diferita a unitatii monetare la momente de timp diferite. Aici apar notiunile duale de dobinda si de factor de depreciere.

O unitate monetara (1UM) depusa in planul de pensii la momentul t = 0 valoreaza la momentul t = 1 q₁ lei. Ne putem imagina ca sunt depusi la banca; valoarea q₁ - 1 este dobinda la momentul t = 1. Presupunind ca la momentele t = j dobinda va fi q_j - 1 , atunci 1 UM la momentul t = 0 valoreaza q₁q₂.q_j UM la momentul j.

Scriind q_j = e^d(j) relatia se mai poate scrie

1 UM la momentul t = 0 = e^{d d d(j)} UM la momentul j.

Invers, daca judecam planul de pensii la momentul t = 0, 1UM depus la momentul t = j valoreaza e^{- d d d(j)} UM la momentul 0. Tinind seama de aceste considerente, suma depusa de asigurat devine, actualizata la momentul t = 0

S_A = a₀ + a₁e ^-d + a₂e^{- d d} + .+ a_{m T}e^{-d d d(m T}

cea platita de asigurator devine

S_S = (s₀ e^{-d d d(m)} + s₁ e^{-d d d(m+1)} + .+ s_T e^{-d d d(T)})1_{(T m)}

Conditia ca planul sa fie echitabil ramine aceeasi, anume (1.7)

Relatiile (1.9)-(1.10) sunt incomod de tratat matematic. In principiu T este o variabila aleatoare pozitiva, nu neaparat cu valori intregi. Poate fi si absolut continua - si de fapt asa se si considera. De aceea este mai comod de facut o aproximare continua, astfel: postulam existenta unei intensitati a platilor efectuate de asigurat a(t) , a unei intensitati a platilor efectuate de asigurator s(t) si a unei dobinzi instantanee e^d(t) (corespunzatoare unui factor de depreciere instantaneu e^-d(t) ) de asa maniera incit suma platita de asigurat pe o unitate de timp intre momentul t si t+1 sa fie . Atunci un plan de pensie este o pereche de functii (a,s) cu a:[0,m] R si s: [m, R functii integrabile. Valoarile actualizate la momentul t = 0 a platilor facute de asigurat si asigurator devin

S_A = , S_S = =

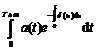
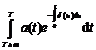
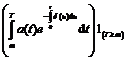
Tinind seama de formula

Ef(T) - f(0) = =

valabila daca T 0 si daca f este derivabila pe portiuni, obtinem

PROPOZITIA 1.1. Conditia ca planul (a,s) sa fie echitabil este ca

=

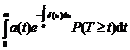
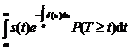
Demonstratie. Functia f(x) = este derivabila in afara punctului x = m si f'(x) = 1_(0,m) . De asemenea, functia g(x) = este de asemenea derivabila (cu exceptia aceluiasi x = m) si g'(x) = . Cum f(0) = g(0) = 0 formula (1.12) devine E(S_A) = Ef(T) = si E(S_S) = Eg(T) =

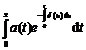
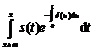
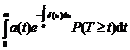
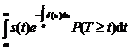
Devine importanta variabila aleatoare (T-m)1_{(T m)}, caci ea arata cit mai are de trait A dupa ce iese la pensie. Actuarii prefera sa lucreze cu variabila aleatoare T_(m) avind repartitia lui T - m conditionata de faptul ca T m. O notatie universal acceptata - desi nu chiar corecta pentru matematician - pentru T_(m) este

T_(m) = (T - m T m)

adica T - m in ipoteza ca T m. In scrierea noastra, T_(m) este o variabila aleatoare cu proprietatea ca

P(T_(m) t) = P(T t +m T t)

Notiuni fundamentale legate de timpul de viata

Fie T 0 o variabila aleatoare interpretata ca fiind timpul de viata al unui asigurat, incepind de la data inceperii planului de asigurare (a,s). Functia sa de repartitie o vom nota F = F_T deci F(x) = P(T x). Se va folosi de asemenea functia F(x) = P(T x) = 1 - F(x-0). Aceasta se numeste functia de supravietuire. In cazul in care T are densitate, aceasta se va nota f = f_T .

Prin variabila aleatoare absolut continua vom intelege o notiune mai restrictiva decit cea cu care se lucreaza de obicei. Vom face ipoteza ca densitatea sa este continua la dreapta , eventual cu exceptia punctului x = 0. In cazul acesta functia de repartitie F este continua, derivabila la dreapta si dt = F(x). In plus in acest caz este verificata relatia F(x) = 1 - F(x). Majoritatea repartitiilor absolut continue in sens obisnuit folosite in statistica satisfac aceasta proprietate. Punem aceasta conditie pentru a avea asigurata relatia F' = f peste tot si nu numai l-a.p.t. cum

Vom nota cu R = R_T opusul logaritmului functiei de supravietuire, adica R(x) = log F(x). Deci F = e^-R .

Un rol important il joaca cantitatea

r_T(x,h) = = P(T < x + h T x)

numita riscul de moarte pe intervalul (x, x+h). Deci este probabilitatea de deces a asiguratului A in intervalul (x,x+h) stiind ca au supravietuit pina la momentul x, impartita la lungimea intervalului. In termeni de functie de supravietuire, relatia devine

r_T(x,h) = =

In caz ca T este absolut continua exista limita r_T(x,0+0) = = . Aceasta cantitate poarta diferite nume, depinzind de autori. Notiunea se pare ca a fost introdusa in teoria fiabilitatii, sub numele de rata de defectare (failure rate, risque de panne). ( Gnedenko, B., Beliaev Y., Soloviev A. , Methodes Mathematiques dans la Theorie de la Fiabilite, Mir 1972; Barlow si Proschan 1965) . In acest context functia F poarta numele de functie de fiabilitate si se noteaza de multi autori cu P = P_T . A se remarca faptul ca exista o analogie izbitoare intre teoria fiabilitatii - care studiaza timpul de functionare a componentelor unui ansamblu - si actuariat sau demografie care studiaza acelasi lucru la organisme vii. In actuariat ( adica stiinta asigurarilor) cantitatea r_T(x,0+0) poarta de asemenea diferite nume : unii ii spun forta de mortalitate (Goovaerts, M.J., Kaas, R., Van Herwaarden, A. E., Bauwelinckx T.: Effective actuarial methods, North Holland 1990) altii risc instantaneu de moarte (Burlacu, V., Cenusa Gh., Bazele matematice ale teoriei asigurarilor, Bucuresti 2000) . Fiind un curs de actuariat, ii vom spune si noi risc de moarte.

In teoria fiabilitatii riscul de moarte se noteaza cu r_T (Barlow si Proschan) sau l_T (Karlin, Gnedenko) iar in actuariat cu m m_T . Noi il vom nota cu r_T(x) , folosind litera m in alte scopuri. Atragem atentia ca in textele de actuariat functia de supravietuire se noteaza cu p = p_T .

Asadar

r_T(x) : = r_T(x,0+0) = = (- logF(x))' = R'(x)

Ca atare , din (2.2) deducem relatiile

R_T(x) = dt si r_T(x,h) =

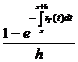
(A se nota ca relatiile de mai sus au sens deoarece am presupus densitatea f continua la dreapta, ca sa nu avem probleme cu derivatele)

Reciproc, orice repartitie absolut continua pe [0, m = fgl este unic determinata de functia sa de risc r prin relatia (2.4) : deci F(x) = . Daca (x)dx = variabila aleatoare T m este finita a.s. iar daca (x)dx < atunci P(T = ) = .

Notiunea de risc de moarte are si un analog discret. Daca variabila aleatoare T ia numai valori de forma dn cu n I N cu d > 0 (altfel zis are o repartitie laticeala) atunci definim

r_T dn) = (deci r_T(dn,h) = )

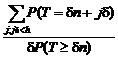
In cazul particular in care T(W N , T , atunci (2.5) devine

r_T(n) = (deci r_T(n,h) = )

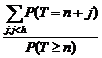
In acest ultim caz este usor de vazut ca daca notam a_n = r_T(n) atunci

p₀ = a , p₁ = (1- a a ,., p_n = (1- a a_n- a_n si n T F(n) = (1- a a_n-

Pentru fiecare h fixat domeniul de definitie al functiei x a r_T(x,h) este 0,M) unde M = ║T║ = ess sup T. Deci, daca T este din L - esential marginita - atunci domeniul de definitie depinde de T, ceea ce este neplacut. Daca insa observam ca x < T F(x) = 1, atunci putem extinde domeniul de definitie al riscului de moarte pe intervalul (- , M), ceea ce nu rezolva inca problema definirii lui r_T(x,h) pentru orice x. Facem de aceea urmatoarea

Conventie daca x ║T║ atunci r_T(x,h) = . Daca T este absolut continua, atunci x ║T║ T r_T(x) = iar daca T are repartitie laticeala pe dN atunci atunci x ║T║ T r_T(x) = .

Motivul este dat de urmatoarele proprietati simple ale lui r :

PROPOZITIA 2.1. Fie T I L o variabila aleatoare nenegativa, h > 0 si M = ║T║

(i). Daca x < M atunci r_T(x,h) . Mai mult, r_T(M-0 , h) = .

(ii). Daca T este absolut continua si densitatea sa f este monotona pe un interval (M-d, M) , d > 0 , atunci limita r_T(M - 0) exista si este egala cu +

(iii). Daca T are o repartitie laticeala atunci r_T(M) =

Demonstratie. (i). r_T(x,h) = = . Daca M - h < x < M , atunci nu avem decit sa observam ca x > M - h , T T M (a.s.) < x + h deci P( x T < x + h) = P(x T) T r_T(x,h) = . (ii): fie a = f(M-0). Limita exista, deoarece am presupus ca f este momotona pe un interval (M-d,M). Avem de calculat . Daca a > 0, limita este = ; daca a = 0, atunci f nu poate decit sa descreasca pe intervalul (x,M) daca M-d < x < M si, mai mult, x < M T f(x) > 0 (altfel s-ar incalca definitia lui M = ║T║ : daca f ar coincide cu 0 pe un interval (M-d, M) ar trebui ca T M-d (a.s.), fals). Atunci dt f(x)(M - x) de unde = . In sfirsit, (iii) este evident: r_T(M) = = , caci M = ess sup T = sup dn│ P(T = dn) > 0) = max dn│ P(T = dn) > 0) (caci multimea respectiva este finita!) deci P(T = M) = P(T M) > 0.

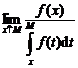
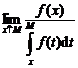
Observatie. Coeficientii r_T au sens si daca variabila aleatoare T nu este neaparat pozitiva. Ceea ce nu mai este adevarat este relatia F(x) = , caci acum F(0) nu mai este neaparat chiar 0.

Comportarea riscului de moarte fata de operatia de scalare. Prin scalare intelegem inlocuirea variabilei aleatoare T cu variabila T' = aT+b

PROPOZITIA 2.2. (i). Daca a > 0, atunci r_aT+b(x,h) = r_T( , ); daca T are densitate atunci r_aT+b(x) = r_T( )

(ii). r_T+b(x,h) = r_T(x-b,h) ; daca T are densitate, atunci r_T+b(x) = r_T(x-b).

Demonstratie. F_aT+b(x) = P(aT+b x) = P(T ) = F( ) deci r_aT+b(x,h) = = r_T( , ).

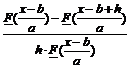
Riscul de moarte al timpului rezidual de viata. Aici formula este deosebit de simpla.

PROPOZITIA 2.3. Fie T un timp de viata si m 0. Atunci (x,h ) = r_T(x+m,h) iar daca T admite densitate atunci (x) = r_T(x+m)

Demonstratie. (x,h ) = = = r_T(x+m,h). Pentru a doua relatie trecem la limita cind h

Comportarea riscului de moarte la operatia de discretizare. Operatia de discretizare consta in inlocuirea variabilei aleatoare T cu discretizata ei T^(d d . Variabila aleatoare T^(d aproximeaza uniform pe T si ia valori in multimea dZ

PROPOZITIA 2.4. Fie r^(d (x,h) riscul de moarte al variabilei discretizate T^(d . Atunci

= r^(d (kd d) = r_T(kd d

Demonstratie. Observam ca P(kd T^(d < kd d) = P(k < k+1) = P( = k) = P(kd T < kd d) iar P( T^(d kd) = P( k) = P( T kd) . Deci dr ^d (kd d) = P(kd T^(d < kd d) / P( T^(d kd) = P(kd T < kd d)/ P( T kd dr_T(kd d

Dintre operatiile cu variabile aleatoare independente, singura fata de care riscul de moarte se comporta acceptabil este operatia de minim.

PROPOZITIA 2.5. Fie X,Y doua variabile aleatoare pozitive independente. Atunci

r_{X Y}(x,h) = r_X(x,h) + r_Y(x,h) - hr_X(x,h)r_Y(x,h)

In consecinta , daca X si Y sunt absolut continue

r_{X Y}(x) = r_X(x) + r_Y(x) si r_{X Y} r_X r_Y

iar daca sunt repartizate pe o retea de pas d

r_{X Y}(x) = r_X(x) + r_Y(y) - dr_X(x)r_Y(x)

Demonstratie. Folosind independenta variabilelor aleatoare X si Y deducem ca

P(X Y x) = P(X x, Y x) = P(X x)P(Y x) = F(x)G(x) unde F si G sunt functiile de supravietuire ale variabilelor aleatoare X si Y. Deci

r_{X Y}(x,h) = = =

= r_Y(x,h) + .

Dar din (2.2) hr_Y(x,h) = 1 - G(x+h)/G(x) T G(x+h)/G(x) = 1 - hr_Y(x,h).

Inlocuind , deducem ca r_{X Y}(x,h) = r_Y(x,h) + r_X(x,h)(1 - h r_Y(x,h)), adica (2.7). Egalitatea de la 2.8 se obtine facind h 0 iar inegalitatea este evidenta : chiar din definitia (2.1) este clar ca hr_Y si hr_Y

In legatura cu riscul de moarte al variabilei "timp rezidual de viata" avem urmatoarea formula:

PROPOZITIA 2.6. Fie m 0. Atunci pentru orice x,h 0 este valabila relatia

= r_T(x+m,h).

In cazul in care T este absolut continua sau repartizata pe reteaua dN, atunci = r_T(x+m). In al doilea caz se subintelege ca x,m I dN.

Demonstratie. Folosim (2.1): = = = = r_T(x+m,h).

Precizam acum comportarea riscului de moarte relativ la diferitele tipuri de convergenta..

PROPOZITIA 2.7.

(i). Daca T_n converg la T in repartitie si T este continua, atunci r_T(x,h) x I A, h > 0.

(ii). Daca T_n sunt absolut continue cu densitatile f_n iar T are densitatea f si f_n f , atunci r_T

(iii). Daca T_n = nT /n si T este absolut continua atunci r_T(x) in toate punctele de continuitate ale lui r_T .

Demonstratie. (i). Este imediat. Fie F_n si F functiile de repartitie ale variabilelor aleatoare T_n si T. Cum F este continua si T_n converge la T in repartitie, inseamna ca F_n converge la F ; deci = converge la = r_T(x,h). (ii). este evident. (iii):Fie x 0. Atunci = = . Fie k_x I N astfel ca k_x nx < k_x+ 1. Sunt doua posibilitati: sau x = k_x/n si atunci = = r_T(x, ) sau k_x < nx < k_x+ 1, in care caz = = r_T( , ). Sa notam x_n = in primul caz si x_n = in al doilea caz. Deci x_n x (deci F(x_n) F(x)!) si = r_T(x_n , ) = .

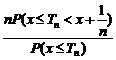
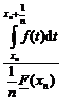
Sa presupunem ca f este continua in x. Deci pentru orice e > 0 exista d > 0 ca x - d < t < x+d T f(x) - e < f(t) < f(x) + e . Daca n este suficient de mare atunci x - d < x_n < x_n + < x + d T de unde rezulta imediat ca lim_n = r_T(x).

Un rol important il joaca in aceasta teorie variabilele aleatoare exponentiale si analogul lor discret, cele geometrice. Ele sunt singurele pentru care riscul instantaneu de moarte este constant.

PROPOZITIA 2.8. Daca r_X (x,h) = r(h) (nu depinde de x) atunci X este repartizata exponential: exista a>0 ca X e_a , adica F(x) = e^-ax1 (x). Daca X are repartitie in reteaua dN d>0 atunci X/d are o repartitie geometrica.

Demonstratie. Din (2.2) deducem ca marimea nu depinde de x. Inseamna ca R(x+h) - R(x) = j(h) x. Functia j A este continua la stinga (caci lim_d j(h-d) = lim_d (R(x+h - d) - R(x)) = R(x+h) - R(x) = j d) - am folosit continuitatea la stinga a functiei R = - logF !) coincide cu 0 daca h = 0 si este aditiva, adica ca j(h+k) = j(h)+j(k) h,k 0 (deoarece j(h+k) = R(x+h+k) - R(x) = (R(x+h+k) - R(x+h)) + (R(x+h) - R(x)) = j(k) + j(h)!) . Atunci j(h) = hj(1) pentru h 0 numar rational. Inseamna ca j(h) = hj h 0 (orice numar h > 0 se poate aproxima de la stinga cu un sir de numere rationale!). Fie a = j(1). Evident a 0 caci in caz contrar R = const, absurd - functia de supravietuire nu poate fi constanta decit daca X s , caz exclus. Am descoperit ca R(x+h) - R(x) = ah x 0. In particular, pentru x = 0 deducem ca R(h) - R(0) = ah . Dar R(0) = 0, deoarece X T F(0) = 1. Deci R(h) = ah. Mai mult, R T a > 0. In concluzie F(x) = e^-ax1 (x) deci X e_a.

Cazul discret. Fie X' = X/d. X' are atunci valori numere naturale. Fie q = r_X'(n) - nu depinde de n. Din (2.7) rezulta ca F_X'(n) = qⁿ, adica X' este repartizata geometric.

Relatia de dominare "p_m". Proprietati simple

Definitie. Fie X,Y doua variabile aleatoare pozitive. Spunem ca X este dominat de Y in sensul riscului de moarte daca r_X(x,h) r_Y(x,h) x 0, h > 0. Scriem in acest caz X p_m Y .

Observatie. Se pare ca notiunea provine din teoria fiabilitatii. Poate fi intilnita in teoria asteptarii sau a proceselor de reinnoire sub diferite alte nume sau notatii cum ar fi: "hazard rate domination "( S.M. ROSS, Stochastic Processes, Bell System Wiley, New York, (1983 sau Barlow, R. and F. Proschan (1975). Statistical Theory of Reliability and Life Testing: Probability Models, Holt, Rinehart and Winston, New York. Barlow, R. and F. Proschan (1965). Mathematical Theory of Reliability, John Wiley, New York., Shaked si Shantikumar 1994) Se mai noteaza in acest caz cu "X p_hr Y". De fapt este o relatie de ordine intre repartitii; are deci sens sa scriem mai degraba "m p_m n" unde m si n sunt doua repartitii pe dreapta.

Dam acum unele caracterizari echivalente ale acestei relatii.

PROPOZITIA 3.1. Fie X si Y doua variabile aleatoare pozitive. Fie F si G functiile lor de supravietuire . Urmatoarele afirmatii sunt echivalente.

(i).    X p_m Y

(ii).    x,h

(ii') x,y I G, x y unde G este o multime densa in [0,

(iii)          X_(t) p_st Y_(t) t

(iv)          X_(t) p_m Y_(t) t

In consecinta, facind in (iii) t = 0 deducem ca X p_m Y T X p_st Y .

Demonstratie

(i) (ii). Din (2.2) X p_m Y F(x)G(x+h) - G(x)F(x+h)

(ii) (ii'). Functia det(x,y) = este continua la stinga. Conditia (ii) este echivalenta cu "det(x,y) x y ", deci evident (ii) T (ii'). Sa presupunem ca este adevarata conditia (ii'). Daca x = 0, det(0,y) = 0, deci nu este nimic de demonstrat; la fel, det(x,x) = 0 x deci putem presupun ca x > 0 si y > x. Cum G este densa, exista sirurile (x_n)_n, (y_n)_n de elemente din G astfel ca x_n y_n si x_n x, y_n y , x_n y_n n. Din continuitatea la stinga avem det(x,y) = lim_n det(x_n, y_n)

(i) (iii). Functiile de supravietuire : pentru X_(t)­ este P(X_(t) h) = P(X - t h│ X t) = P(X t+h│X t) = iar pentru Y_(t) este P(X_(t) h) = . Atunci X p_m Y adica functia de supravietuire a lui X_(t) nu o depaseste pe cea a lui Y_(t) : P(X_(x) h) P(Y_(x) h) h 0 ceea ce este echivalent cu X_(x) p_st Y (vezi lectia despre dominare stocastica).

(i) (iv). Din Propozitia (2.6) avem = r_X(x+t,h) si = r_Y(x+t,h). Deci X p_m Y r_X(x,h) r_Y(x,h) x 0, h > 0 r_X(x+t,h) r_Y(x+t,h) x,t,h X_(t) p_m Y_(t) t

In cazul variabilelor aleatoare absolut continue sau discrete, dar cu valori in reteaua dN d > 0, se poate spune mai mult.

PROPOZITIA 3.2. Daca X,Y sunt absolut continue sau discrete cu valori in reteaua dN d > 0 atunci    X p_m Y r_X(x) r_Y(x) x I A (in al doilea caz x I dN

Demonstratie. "T": Daca X,Y sunt absolut continue, atunci exista limitele r_X(x,0+0) := r_X(x) respectiv r_Y(x,0+0) := r_Y(x) . Evident ca r_X(x,h) r_Y(x,h) h > 0 T r_X(x,0+0) r_Y(x,0+0). In al doilea caz, r_X(kd) nu inseamna altceva decit r_X(kd d

". Daca X,Y sunt absolut continue, avem din (2.4) r_X(x,h) = , r_Y(x,h) = . Evident ca r_X r_Y T r_X(x,h) r_Y(x,h).

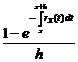
Sa presupunem ca X,Y au valori in d N . Fie x = kd.Daca h < d nu avem nimic de demonstrat, deoarece r_X(kd,h) = r_X(kd d) = r_X(kd). Presupunem ca h = nd + r cu 0 r < d. Atunci sa notam cu X',Y' noile variabile aleatoare X/d si Y/d. Acestea vor avea valori naturale. Fie a_j = r_X'(j) si b_j = r_Y'(j). Din ipoteza stim ca a_j b_j j 0. Din (2.7) rezulta ca F_X'(m) = (1-a a_j- ) si F_Y'(m) = (1-b b_j- j 1. Sa remarcam ca r_X(kd,h) = P(kd dX' < (k+n)d + r)/dP(kd dX') = P(k X' < (k+n) + r/d dP(k X') = r_X'(k,m) ( unde m = n daca r = 0 si m = n+1 daca r 0) = de unde r_X(kd,h) =1- (1-a_k a_k+ a_k+m- ) (am aplicat (2.7)! ) .Analog r_Y(kd,h) =1- (1-b_k b_k+ b_k+m- ). Acum concluzia este evidenta: a_j b_j T a_j b_j T a_k a_k+ a_k+m- b_k b_k+ b_k+m- T r_X(kd,h) r_Y(kd,h).

Exemplu.3.1. Daca X = a, Y = b sunt constante si a b atunci X p_m Y.

Intr-adevar, = 1_{(- ,a ,b} (x,x+h) - 1_{(- ,b ,a} (x,x+h) = 1_{(- ,a (a,b} (x,x+h) 0. Sau direct: r_X(x,h) = 1_(a-h, (x) 1_(b-h, (x) = r_Y(x,h). Scrisa in termeni de repartitii, relatia devine

a b T e_a p_m e_b

Dimpotriva, nu este adevarat ca X p_m X + a daca a

Contraexemplu. 3.2. Fie X astfel ca F(x) = 1 . Aceasta corespunde densitatii f(x) = si riscului instantaneu de moarte r_X(x) = (x). Pentru variabila aleatoare Y = X+a avem (fie calcul direct, fie folosim propozitia 2.2(ii)!) r_Y(x) = r_X(x-a) = _a+ (x). Pe intervalul (- ,a+1) este adevarat ca r_X r_Y , dar pe a+ ) este valabila exact inegalitatea inversa: r_X(x) = < r_Y(x) =

Definitie Daca X p_m X + a a 0 spunem ca X are rata crescinda de mortalitate. Vom nota acest lucru prin "X I IFR". Aceasta este notatia internationala si provine din teoria fiabilitatii : o prescurtare de la "Increasing Failure Rate". Notatia in termeni de repartitii ar fi "m I IFR"

Invarianta relatiei "p_m" la minim.

PROPOZITIA 3.3. Fie X,Y si X', Y' doua perechi de variabile aleatoare independente.

Daca X p_m X' si Y p_m Y' , atunci X Y p_m X' Y'

Demonstratie. Fie x,h >0. Fie a = r_X(x,h), b = r_Y(x,h), a' = r_X'(x,h) si b' = r_Y'(x,h). Din (2.7) stim ca r_{X Y}(x,h) = a + b - hab, r_{X' Y'}(x,h) = a' + b' - ha'b' . Din ipoteza a a', b b' . Vrem sa aratam ca

a + b - hab a' + b' - ha'b' a - a' + b -b' hab - ha'b'.

Dar hab - ha'b' = ha(b-b') + hb'(a-a') ( b -b') + (a - a') deoarece intotdeauna hr_T(x,h) 1 (din 2.1).

Invarianta relatiei "p_m" la operatia de scalare.

PROPOZITIA 3.4. Fie X,Y doua variabile aleatoare. Daca X p_m Y, atunci aX+b p_m aY+b pentru orice a,b

Demonstratie. Aplicam propozitia 2.2: r_aX+b(x,h) = r_X( , );) r_aY+b(x,h) = r_Y( ).

Observatie. Notiunea are sens si pentru variabile aleatoare nu neaparat pozitive; puteam accepta si b I A oarecare.

Invarianta relatiei "p_m" la operatia de discretizare.

PROPOZITIA 3.5. Fie X,Y doua variabile aleatoare pozitive. Daca X p_m Y, atunci aX p_m aY pentru orice a

Demonstratie. Fie X' = aX si Y' = aY . Cum acestea iau valori numere naturale, din propozitia 3.2 este suficient sa aratam ca r_X'(k) r_Y'(k) k natural. Dar P(X' = k)/P(X' k) = P(k aX<k+1)/P(k aX) = P(k/a X <k/a+1/a)/P(k/a X) = r_X(k/a, 1/a)/a r_Y(k/a, 1/a)/a = r_Xt(k).

Invarianta relatiei "p_m" la convergenta slaba.

PROPOZITIA 3.6. Daca m_n T m n_n T n sunt repartitii pe dreapta atunci

m_n p_m n_n n T m p_m n

Demonstratie. Functiile de supravietuire F_n (x) := m_n x, )) converg la F(x) = m x, )) in toate punctele de continuitate ale lui F iar G_n (x) := n_n x, )) converg la G(x) = n x, )) in toate punctele de continuitate ale lui G. Fie G x F si G sunt continue in x . Cum G^c este o multime cel mult numarabila, G este densa in [0, ). Putem aplica echivalenta (i) (ii') din Propozitia 3.1.

Intr-adevar, functiile det_n(x,y) := converg la det(x,y) := pentru (x,y) I G G, apoi m_n p_m n_n det_n(x,y) x y ; deci det(x,y) = lim_n det_n(x,y) (x,y) I G G , x y . Or, conditia det(x,y) x y, x,y I G este chivalenta cu "m p_m n

Contraexemplu 3.3. Relatia "p_m" nu este invarianta nici la maxim, nici la convolutie si nici la mixtura.

1. Fie X,Y doua variabile aleatoare exponentiale independente: X e_a, Y e_b, b > a. Vom arata ca relatia X p_m X Y este falsa. Cele doua variabile aleatoare sunt absolut continui, de aceea va fi suficient sa aratam ca nu este adevarat ca r_{X Y} r_X.

Din Propozitia 2.8 vedem ca r_X = a, r_Y = b . Apoi, cum X si Y sunt independente avem ca F_{X Y}(x) = P(X Y x) = P(X x) + P(Y x) - P(X x) P(Y x) = e^-ax + e^-bx - e^{- (a+b)x} de unde, derivind, gasim ca densitatea este f_{X Y}(x) = (a e^-ax + be^-bx -(a+b) e^{- (a+b)x})1 (x) deci, simplificind cu e^-(a+b)x rezulta

r_{X Y}(x) =

Inegalitatea r_{X Y} r_X devine ae^bx + be^ax- a - b ae^ax + ae^bx - a be^ax - b ae^ax (b-a)e^ax b x care este evident falsa: daca x termenul sting al inegalitatii tinde la

Deci nu numai ca se poate ca X p_m X', Y p_m Y' , X,Y si X',Y' independente dar sa nu fie adevarat ca X Y p_m X' Y' ci se poate si mai rau : X = X', Y = 0 si totusi X = X 0 sa nu fie dominat de X' Y'.

Se poate folosi chiar contraexemplul 3.2: X p_m X, 0 p_m a dar e fals ca X+0 p_m X + a.

Vom arata ca se pot construi repartitii m m n n' pe ) astfel ca m p_m m n p_m n' si totusi relatia pm + qn p_m pm' + qn' sa fie falsa (p+q = 1, p,q 0!) . Vom lua chiar mai mult: repartitii exponentiale: m m' = e_a , n = e_b+h si n' = e_b si p = q = ½ . Fie X pm + qn si Y pm' + qn' . Presupunem 0 <a < b .

Calculam densitatile si riscurile instantanee de moarte r_X si r_Y . Rezulta

r_X(x) = =

r_Y (x) = =

Pretindem ca pentru orice x > 0 se poate alege h astfel ca r_X(x) < r_Y(x). Intr-adevar, fie x > 0 fixat. Daca facem h atunci r_X(x) a < . Aceasta contrazice ipoteza ca r_X r_Y , adica X p_m Y sau in termeni de repartitii ca ar putea fi adevarata relatia pm + qn p_m pm' + qn

Observatie. In teoria fiabilitatii operatiile acestea sunt importante. Sa spunem ca X si Y sunt timpii de viata ai unor componente ale unui aparat. De multe ori - in cazurile cele mai simple- putem accepta ca X si Y sunt independente. De exemplu X ar pute fi durata de viata a platinii unui automobil iar Y cea a condensatorului. In cazul in care componentele sunt in paralel - adica aparatul nu functioneaza decit daca ambele componente functioneaza (cum este exemplul nostru cu platina si condensatorul) atunci X Y este durata de functionare a dispozitivului (in cazul nostru, daca una din piese nu functioneaza, masina nu merge). Fata de aceasta operatie relatia "p_m" se comporta bine: daca ai platina si condensator de calitate mai buna (cu risc instantaneu de defectare mai mic) atunci masina va merge mai mult fara defectiuni decit daca iei piese de calitate mai slaba. Din punct de vedere actuarial o asemenea situatie ar putea aparea daca cineva isi depune banii a o banca si isi stabileste un imputernicit care sa poata face operatiuni in cont: daca unul din ei moare, contractul cade. Sau daca isi propune sa depuna bani la o banca pina la un moment Y cind isi va putea cumpara o vila: depune pina la momentul X Y, X fiind durata sa de viata.

Se mai poate si altfel: componentele sa fie legate in serie. Ca sa revenim la exemplu cu masina. bujiile sunt legate in serie. Daca, sa zicem, avem un motor cu doua bujii - de exemplu un Trabant - el merge (cum merge, este alta problema) atita vreme cit mai functioneaza o bujie. Daca X,Y sunt timpii de functionare al bujiilor, atunci X Y va fi timpul cit, teoretic, motorul poate sa functioneze. Din punct de vedere actuarial un exemplu analog ar fi durata de timp in care se plateste pensia unei familii formata din doi pensionari. S-ar putea da probabil si exemple mai inteligente.

Se poate si asa: componentele cu durata de viata X si Y sunt puse in serie, dar a doua nu incepe sa functioneze decit atunci cind prima se defecteaza.Componentele sunt deci legate in serie cu inlocuire.Daca tot am vorbit de masini,ne putem gindi la roata de rezerva: X este timpul pina la prima pana de cauciuc, Y este timpul de la inlocuirea rotii defecte cu cea de rezerva pina la urmatoarea pana. Atunci durata de functionare a aparatului va fi X+Y. Nu e nevoie sa argumentam imortanta convolutiei in actuariat. Ajunge sa ne gindim ca suma platita de o societate de asigurari este o suma de variabile aleatoare care in majoritatea cazurilor se pot presupune independente.

In fine, operatia de mixtura corespunde urmatoarei situatii: avem mai multe componente, produse de firme diferite, avind repartitii diferite ale duratei de viata. Daca repartitiile lor sunt m m_n si luam o piesa la intimplare (de exemplu am amestecat piesele si nu mai stim firma care le-a produs) atunci repartitia timpului de viata al piesei alese va fi, apriori p₁m + .+ p_nm_n unde p_j este probabilitatea ca piesa sa fie din lotul "j". In actuariat o asemenea situatie este tipica unei abordari bayesiene (vezi capitolul despre teoria credibilitatii).

Relatia de ordine "p_m" se comporta bine asadar numai fata de prima operatie: de minim.

Si totusi, in anumite conditii suplimentare, se comporta bine si fata de convolutie.

Invarianta relatiei "p_m la convolutii cu repartitii IFR

Am vazut in contraexemplele 3.3. ca relatia de dominare "p_m" nu este invarianta la operatia de convolutie. Acum vom demonstra ca, totusi, daca repartitiile au unele proprietati suplimentare invarianta la convolutii poate fi salvata.

Reamintim ca o repartitie pe [0, m este de tip IFR daca X p_m X + a a 0 unde X este o variabila aleatoare repartizata X ~ m

Folosind propozitia 3.1. deducem urmatoarea caracterizare a acestor repartitii

PROPOZITIA 4.1. Fie X o variabila aleatoare pozitiva cu functia de supravietuire F.

Atunci X I IFR x I A, a,h X + a p_m X + b a < b.

Demonstratie. Functia de supravietuire a variabilei X + a este G(x) = P(X + a x) = F(x-a). Propozitia 3.1 arata ca relatia X p_m X + a este echivalenta cu h 0. In legatura cu a doua echivalenta, ea este imediata. Nu avem decit sa inlocuim in determinantul de mai sus pe x cu x-a si pe a cu b-a . Obtinem

Observatie. Atit propozitia 3.1 cit si propozitia 4.1 sunt adevarate si pentru variabile aleatoare oarecare, nu neaparat pozitive. Notiunile "IFR" si "p_m" au sens si pentru variabile aleatoare oarecare iar in demonstratia echivalentelor de la Prop. 3.1 nu s-a folosit nicaieri pozitivitatea lui X si Y.

PROPOZITIA 4.2. Fie X o variabila aleatoare pozitiva nemarginita, F functia sa de supravietuire si R(x) = - lnF(x).

Atunci X I IFR     R este convexa

In concluzie orice variabila aleatoare nemarginita de tip IFR este absolut continua.

Demonstratie. Aplicam propozitia anterioara. Avem :

F(x) = e^{- R(x)}, F(x+h) = e^{- R(x+h)}, F(x - a) = e^{- R(x-a)}, F(x - a + h) = e^{- R(x+h - a)}

deci R(x) - R(x-a) R(x+h) - R(x+h-a) x I R, a,h

Altfel spus diferenta x a R(x) - R(x-a) este o functie crescatoare. Dar aceasta este o caracterizare a convexitatii (o aplicare imediata a inegalitatii coardelor!) .

Fiind convexa, functia R: A A este si continua si derivabila la dreapta. Fie r = R', unde derivata este inteleasa ca fiind derivata la dreapta. Cum R este convexa, r este crescatoare si continua la dreapta (deci continua cu exceptia unei multimi cel mult numarabile, deci neglijabile Lebesgue).

Inseamna ca si F este continua si derivabila la dreapta. Derivata sa este F'(x) = - r(x)F(x) va fi de asemenea continua la dreapta si, fiind marginita pe orice interval compact si continua cu exceptia unei multimi cel mult numarabile, va fi integrabila Riemann. Mai [Z1] mult, este valabila formula Leibniz-Newton[1] F(b) - F(a) = . Daca vom pune f(x) = - F'(x) atunci aceasta va fi o densitate pentru repartitia lui X. Ca atare, X este absolut continua.

Observatie. Dar daca X este marginita ? Atunci nu mai este adevarat ca X I IFR T X absolut continua. De exemplu orice variabila aleatoare constanta este de tip IFR (a T X p_m X + a !) . Ramine adevarat insa R : I ) este continua, derivabila pe intervalul I = x R(x) := (a,b). Avem doua cazuri:

sau = ; in acest caz F(b) = 0, deci X este absolut continua;

sau    < ; atunci F(b) > 0 deci P(X = b) = F(b) - F(b+0) = F(b) > 0 , deci X nu este absolut continua. Repartitia sa este de forma (1- F(b))m + F(b)e_b unde m este o repartitie absolut continua pe intervalul (a,b).

Al doilea caz este tipic daca avem de a face cu variabile aleatoare Y = X b unde X este o variabila aleatoare absolut continua. De exemplu, daca X ~ U(0,1) si Y = X ½ atunci P X ^- = ½ (U(0, ½) + e

Observatie. Unii autori numesc proprietatea "IFR" logconcavitate: adica functia de supravietuire F este logconcava.

Pentru variabilele aleatoare discrete, exista un analog perfect:

Definitie . Fie X o variabila aleatoare cu valori in dZ. Atunci spunem ca X este de tip IFR (scriem X I IFR(d X p_m X + a a I dN

Proprietatea IFR este in acest sens invarianta la operatia de discretizare. Ea este de asemenea invarianta la operatia de scalare.

PROPOZITIA 4.3. Daca X I IFR atunci d I IFR(d d > 0. Mai mult, daca a,b 0 atunci X I IFR T aX + b I IFR

Demonstratie. Fie a = kd si X' = d . Trebuie aratat ca X' p_m X' + a. Dar X p_m X + a , caci X este de tip IFR. Dar relatia "p_m" este invarianta la discretizare si scalare (Propozitia 3.5 si 3.4). Inseamna ca

d p_m d = d = d( + k) = X' + dk sau, altfel spus, X' p_m X' + a.

A doua afirmatie rezulta imediat din Propozitia 4.1:daca a = 0 nu e nimic de demonstrat iar daca a >0 trebuie aratat ca t T aX+b p_m aX+b+t . Dar X I IFR T X p_m X + t/a (definitia) T aX+b p_m a(X+t/a) + b (Propozitia 3.4.) aX+b p_m aX+t+b

Cu aceste pregatiri putem demonstra rezultatul principal al acestei sectiuni.

Mai intii varianta discreta.

TEOREMA 4.4. Fie X₁, X₂ variabile aleatoare pozitive cu valori numere naturale si Y o variabila aleatoare de asemenea cu valori numere naturale si, in plus, de tip IFR.

Daca Y este independenta de X₁ si de X₂ atunci

X p_m X₂ T X₁ + Y p_m X₂ + Y

Sau, in termeni de repartitii: daca m m si n sunt repartitii pe N atunci

m p_m m n I IFR(1) T m n p_m m n

Demonstratie.

Sa fixam mai intii unele notatii. Fie, pentru j I N fixat

p_1,j = P(X₁ = j), p_2,j = P(X₂ = j), q_j = P(Y = j), F_1,j = P(X₁ j), F_2,j = P(X₂ j), G(j) = P(Y j)

Fie de asemenea a b si g riscurile de moarte ale celor trei variabile aleatoare. Deci

a_j = p_1,j /F_1,j , b_j = p_2,j /F_2,j, g_j = q_j /G(j) j I N

cu conventia de la propozitia 2.1: daca F₁(j) = 0, atunci a_j = 1; F₂(j) = 0 T b_j = 1 , G(j) = 0 T g_j

Din ipoteza si din definitia riscului de moarte avem atunci relatiile

a_j b_j p_1,j = a_j F₁(j), p_2,j = b_j F₂(j) , q_j = g_j G(j) j I N

Fie V₁ si V₂ functiile de supravietuire ale variabilelor aleatoare X₁ + Y si X₂ + Y.

Din definitia convolutiei avem

V (a) = , V₂(a) = , a I N

Conform Propozitiei 3.1 avem de demonstrat ca

Sa notam cu V(a,b) determinantul de mai sus. Fie a b doua numere naturale. Daca a = b , atunci V(a,a) = 0, deci nu avem nimic de demonstrat. Presupunem asadar a < b. Avem

V(a,b) = = -

= = + + . Suma din mijloc este egala evident cu 0 ; in cea din urma inlocuim i cu j si j cu i . Obtinem V(a,b) = + deci

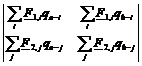
V(a,b) = =

Ultima egalitate este evidenta, deoarece pentru i = j termenul general al ei este egal cu 0. Sa notam cu s_j suma

s_j = =

unde

a_i = , b_i =

(intr-adevar, b_i - b_i-1 = = = - din (4.4))

Pe de alta parte = a_jb_j - a_jb_j-1 + a_j-1b_j-1 - a_j-1b_j-2 + a_j-2b_j-2 - a_j-2b_j-3 + a_j-3b_j-3 - a_j-3b_j-4 + . = a_jb_j + b_j-1(a_j-1 - a_j) + b_j-2(a_j-2 - a_j-1) + b_j-3(a_j-3 - a_j-2) + . = (caci din (4.10) a_jb_j = 0!)

In cazul nostru a_i - a_i+1 = - = = . Inlocuind in (4.9) rezulta

s_j =

Dar , din (4.6) avem : = b_i 0 (conform ipotezei a_i b_i iar 0 caci X₁ p_m X₂ si aplicam Propozitia 3.1 (ii)! ). Pe de alta parte = g_a-j 0 (conform ipotezei Y I IFR, deci sirul (g_n)_n este crescator: cum a < b T b-j a-j T g_b-j g_a-j ; pe de alta parte i < j T a - j < a - i, b - j < b - i si din (2.7) deducem ca G(a-i) = G(a-j)g_a-jg_a-j+ g_a-i- , G(a-i) = G(b-j)g_b-jg_b-j+ g_b-i- deci = G(a-j)G(b-j) (g_b-jg_b-j+ g_b-i- g_a-jg_a-j+ g_a-i- 0 fiindca a < b T g_b-t g_a-t

Am obtinut in definitiv estimarea

s_j g_a-j G(a-j)G(b-j) (g_b-jg_b-j+ g_b-i- g_a-jg_a-j+ g_a-i-

Cu aceasta teorema este demonstrata: nu avem decit sa vedem ca V(a,b) =

TEOREMA 4.5. (invarianta la convolutii cu repartitii IFR)

Fie X₁, X₂, Y₁, Y₂ variabile aleatoare cu valori numere naturale. Presupunem ca X₁ p_m X₂ si Y₁ p Y₂. Daca

(i)       X este independenta de Y₁, X₂ este independenta de Y₂ ;

(ii)     Y si X₂ I IFR sau X₁ si Y₂ I IFR

Atunci X₁ + X₂ p_m Y₁ + Y₂ .

In particular rezultatul este cu atit mai mult valabil daca toate cele patru variabile aleatoare sunt de tip IFR.

Scris in termeni de repartitii rezultatul este : daca m_j n_j sunt repartitii pe N atunci

m p_m m n p_m n I IFR(1) T m n p_m m n

Demonstratie. Putem presupune, lucrind eventual cu alte variante de variabile aleatoare pe un spatiu probabilizat convenabil ales ca (X₁, Y₁) este independent de (X₂, Y₂). Sa presupunem ca Y₁ si X₂ sunt de tip IFR. Din Teorema 4.4 avem atunci implicatia X₁ p_m X₂ T X₁ + Y₁ p_m X₂ + Y₁ . Dar X₂ este de tip IFR, deci X₂ + Y₁ p_m X₂ + Y₂ . Cum relatia " p_m " este tranzitiva rezulta imediat concluzia dorita.

In al doilea caz, adica daca X₁ si Y₂ I IFR(1) atunci Y₁ p_m Y₂ T Y₁ + X₁ p_mY + X₁ p_m Y₂ + X₂ .

In sfirsit, acum putem prezenta rezultatul general.

TEOREMA 4.6. Fie X₁, X₂, Y₁, Y₂ variabile aleatoare pozitive. Presupunem ca X₁ p_m X₂ si Y₁ p_m Y₂. Daca

(i)      X este independenta de Y₁, X₂ este independenta de Y₂ ;

(ii)            Y si X₂ I IFR sau X₁ si Y₂ I IFR

Atunci X₁ + X₂ p_m Y₁ + Y₂

In termeni de repartitii: pentru orice repartitii pe [0, ) este adevarat ca

m p_m m n p_m n I IFR(1) T m n p_m m n

Demonstratie.

Demonstram mai intii ca X₁ p_m X₂, Y I IFR, Y independenta de X₁ si de X₂ T X₁ + Y p_m X₂ + Y. Fie X_1,n =[nX₁]/n, X_2,n = [nX₂]/n, Y_n = [nY]/n. Din Propozitia 3.5. [nX₁] p_m [nX₂]. Din Propozitia 4.3 nY I IFR T [nY] I IFR(1) (propozitia 4.3 cu d = 1) . Mai mult, [nY] este independenta de [nX₁] si de[nX₂]

Inseamna ca [nX₁] +[nY] p_m [nX₂]+ [nY]. Aplicind din nou propozitia 3.4 urmeaza ca

X_1,n + Y_n p_m X_2,n + Y_n n

Dar X_1,n + Y_n (respectiv X_2,n + Y_n ) converge uniform la X₁ + Y (respectiv la X₂ + Y), deci si in repartitie. Din Propozitia 3.6 rezulta atunci ca X₁ + Y p_m X₂ + Y .

Restul demonstratiei este analog celei din Teorema 4.5; schema este aceeasi

X + Y₁ p_m X₂ + Y₁ p_m X₂ + Y₂ .

COROLAR 4.7. Sa presupunem ca X,Y sunt variabile aleatoare independente absolut continue pozitive si X I IFR. Atunci

r_X+Y r_X r_Y

Demonstratie. 0 p_m Y, X p_m X T 0 + X p_m Y + X T r_X r_X+Y . Analog r_Y r_X+Y .

5. Pastrarea proprietatii "IFR" la convolutii

Am vazut in Propozitia 4.3 ca proprietatea IFR este invarianta la operatiunile de scalare si discretizare. Este usor de vazut ca ea este invarianta la operatia de minim precum si la cea de limita slaba .

PROPOZITIA 5.1. Fie X,Y doua variabile aleatoare independente .

Atunci

(i). X,Y I IFR T X Y I IFR.

(ii). Daca X,Y sunt cu valori in N atunci X,Y I IFR(1) T X Y I IFR(1)

(iii). Daca m_n I IFR si m_n T m , atunci m I IFR

Demonstratie. (i).Un mod de a demonstra afirmatia este folosind chiar definitia si Propozitia 3.3: X,Y I IFR X p_m X + a, Y p_m Y + a a 0 . Deci X Y p_m (X + a) (Y + a) = X Y + a. Demonstratia are avantajul ca merge si la punctul (ii), decit ca acum trebuie inlocuit "a 0" cu "aIN" : X,Y I IFR(1) X p_m X + a, Y p_m Y + a a I N

(iii). Fie F_n functiile de supravietuire ale repartitiilor m_n si R_n = - logF_n. Din Propozitia 4.2 acestea sunt functii convexe. Dar limita unui sir de functii convexe este de asemenea o functie convexa, deci m I IFR, folosind din nou Propozitia 4.2

Vom demonstra acum o proprietate importanta a repartitiilor de tip IFR : invarianta la convolutie. In cazul absolut continuu ea a fost demonstrata de Barlow si Proschan in 1965

TEOREMA 5.2. Fie X,Y doua variabile aleatoare independente. Atunci

(i). X,Y I IFR T X + Y I IFR ;

(ii). X,Y I IFR(1) T X + Y I IFR(1) ;

Dimpotriva, nu este adevarat ca X I IFR, Y I IFR(1) T X+Y I IFR

Demonstratie. (i). Trebuie aratat ca X+Y + a p_m X+Y a 0. Daca a = 0 nu este nimic de demonstrat, deci vom presupune ca a > 0. Din ipoteza Y p_m Y + a , caci Y I IFR. Cum X este independenta de Y, ea va fi independenta si de Y + a. Teorema 4.6. , in care punem X₁ = X₂ = X, Y₁ = Y si Y₂ = Y+ a ne spune ca X + Y p_m X + (Y + a). La punctul (ii) demonstratia este similara, dar folosim Teorema 4.5.

Pentru ultima afirmatie, un contraexemplu ar putea fi urmatorul : m = Uniform(0,½ ) , n e e ) / 2. Atunci m n este repartitia uniforma pe (0, ½) (1,1½) care nu mai este de tip IFR.

Observatie. Contraexemplele din paragraful 3 sugereaza ca proprietatea IFR nu este invarianta la operatiile de maxim si de mixtura. Daca luam X e₁ si Y e₂ cu X,Y independente atunci, din (3.3) vedem ca r_{X Y} = , care nu este o functie crescatoare. Ca o mixtura de variabile IFR nu mai e neaparat IFR se poate vedea din relatiile (3.4), (3.5): se poat alege parametrii a,b ca ricurile inatantanee de moarte sa nu fie crescatoare.

Observatie. Exista o notiune duala notiunii de "IFR", folosita mai ales in teoria asteptarii (Ross, Stochastic processes, 1983) , anume aceea de "DFR" (Decreasing Failure Rate) . Daca X este o variabila aleatoare absolut continua si pozitiva, Y I DFR r_X : [0, ) este o functie descrescatoare. Spre deosebire de notiunea "IFR" care are sens pentru orice variabila aleatoare absolut continua, cea de "DFR" nu are sens decit pentru variabile aleatoare marginite inferior, caci nu se poate ca raportul r_X = f_X /F sa fie descrescator pe toata axa reala. Motivul este ca F(x) = ar fi egal cu 0 daca r_X ar fi o functie descrescatoare. Repartitiile de tip DFR corespund timpilor de viata ale componentelor "mai bune folosite decit noi " - de exemplu motorul unei masini. Repartitiile DFR nu sunt invariante la convolutie (de exemplu repartitia exponentiala e_a- care este si IFR si DFR convolutata cu ea insasi da nastere unei repartitii Gamma, care este IFR , dar nu si DFR) in schimb sunt invariante la mixturi. (Vezi de exemplu Ross sau Barlow si Proschan).

Vom trece acum in revista unele repartitii de tip IFR.

PROPOZITIA 5.3. Urmatoarele repartitii discrete sunt de tip IFR(1)

(i). m = (1-p)e + pe

(ii). m = Geometric(p)

(iii). Repartitiile complet decompozabile, adica avind proprietatea ca functia lor generatoare este produs de polinoame de gradul I;

(iii). Binomial(n,p);

(iv). Poisson(l

(v). Repartitia binomiala inversa, adica m := Negbin(n,p) = Geometric(p)*ⁿ

Demonstratie. (i). Calcul direct: r_m(n) = (1-p)1 (n) + 1_[1, (n) este un sir crescator.

(ii). p_n = pqⁿ , F(n) = qⁿ T r_m(n) = p ; repartitia geometrica este analogul discret al exponentialei.

(iii). O repartitie complet decompozabila este de forma m m m m_n unde m_j =(1-p_j)e + p_je ; aplicam Teorema 5.2.

(iv). Binomiala este complet decompozabila.

(iv). Poisson(l) = lim_nBinomial(n,l/n) . Dar se verifica usor si direct.

(v). Aplicam Teorema 5.2.

Observatie. Nu stim daca repartitia hipergeometrica Hipergeometric(a,n ; k) este de tip IFR. Banuim ca da, insa nu am reusit o demonstratie.

Observatie. Punctul (iii) al propozitiei furnizeaza un criteriu de a decide daca o repartitie este complet decompozabila. De exemplu repartitia m e e e ) / 10 nu este decompozabila deoarece r_m , r_m(1) = 0.2 si r_m(n) = 1 (daca n 2) nu este un sir crescator.

Observatie.A se remarca faptul ca in abordarea repartitiilor folosind riscul instantaneu de moarte r_m repartitia exponentiala e_a joaca rolul central: ea este si de tip IFR si de tip DFR. De fapt IFR DFR = EXP, adica repartitiile exponentiale.

Multe repartitii uzuale sunt de tip IFR.

PROPOZITIA 5.4. Urmatoarele repartitii absolut continue sunt de tip IFR:

(i). Uniform(0,1) si deci, prin scalare Uniform(a,b) si prin convolutie, repartitiile triunghiulare;

(ii). Gamma(n,a) daca n 1 deci si c (n) pentru n

(iii). N(m s

(iv). Beta(m+1, n+1) cu m,n

Demonstratie. (i). Fie X Uniform(0,1). Atunci r_X(x) = 1_(0,1)(x)/(1-x) + (x) este o functie crescatoare.

(ii). Daca X Gamma(n,a) atunci X = Y/a unde Y Gamma(n,1). Din invarianta proprietatii IFR la scalare, rezulta ca este suficient de demonstrat ca Y I IFR. Daca n este un numar natural, afirmatia este o consecinta imediata a teoremei 5.2 , deoarece Y este o suma de n variabile aleatoare independente repartizate exponential : Gamma(n,1) = e₁ e e , convolutia facindu-se de n ori. Vom presupune asadar ca n = n +1+ e cu n un numar natural si e I (0,1). Atunci densitatea f_Y va fi de forma f_Y(x) = Cxⁿ e^-x (x). Sa notam p = n - 1 = n + e > 0. Deci

r(x) := r_Y(x) = , x

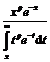
Trebuie aratat ca aceasta functie este crescatoare. Conditia r'(x) 0 devine

(p - x) dt + x^p+1e^-x

Daca 0 x p aceasta este evident. Vom presupune deci x > p si vom scrie (5.2) sub forma

dt

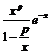
Pentru a demonstra inegalitatea (5.3) vom integra in mod repetat prin parti.Avem :

dt = x^pe^-x+p dt = x^pe^-x+ px^p-1e^-x + p(p-1) dt = . = e^-x(x^p+ px^p-1 + p(p-1)x^p-2 + . + p(p-1).(p-n+1)x^p-n + p(p-1).(p-n) dt .

Dar dt = dt x^e dt (caci e < 1 T e - 1 < 0 deci t < x T t^e < x ^e ) = x^e e^-x

Deducem astfel inegalitatea

dt e^-x( x^p + )

(A se observa ca, daca p este numar natural (5.4) este chiar egalitate!)

Pe de alta parte

= e^-x( x^p + )

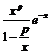
Comparind membrii drepti ai relatiilor (5.4) si (5.5) inegalitatea (5.3) devine evidenta . Deci Y I IFR

In legatura cu repartitia c (n), se stie ca c (n) = Gamma(n /2, ½) .

(iii). Din ratiuni de scalare este suficient de demonstrat ca N(0,1) I IFR. Intr-adevar, daca X N(m s ), atunci X = m sY cu Y N(0,1). De data aceasta rata de mortalitate, r este o functie de finita pe R cu valori pozitive. Mai precis

r(x) = deci r' dt

Daca x 0 inegalitatea de mai sus este evidenta. Daca x > 0 avem dt = dt dt (caci x t!) = .

(iv). La repartitia Beta(m+1,n+1) densitatea este de forma f(x) = C x^m(1-x)ⁿ 1_(0,1)(x) unde C este o constanta de normare (de fapt 1/C = b(m+1,n+1) , nu are importanta). Daca m = n = 0, avem repartitia uniforma care este de tip IFR. Presupunem ca m+ n > 0.Atunci riscul instantaneu de moarte este

r(x) =

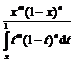
de unde, derivind, rezulta conditia ca r sa fie crescatoare si anume

r' ((m+n)x - m) x^m+1(1-x)ⁿ⁺¹ x

Daca x inegalitatea este evidenta, deoarece membrul sting este negativ iar cel drept pozitiv. Daca < x < 1 inegalitatea este echivalenta cu

< x < 1

Sa notam y = 1-x si sa facem substitutia t := 1- t . Atunci (5.9) devine

0 < y <

Pentru a o demonstra, sa consideram functiile f,g : [0, ) R date prin f(y) = si g(y) = . Vrem sa aratam ca f g. Sa observam ca f(0) = g(0) = 0. Vom arata ca f' g', ceea ce va rezolva problema : functia cu derivata mai mare va fi mai mare. Derivind si scapind de numitori, vedem ca inegalitatea f' g' este echivalenta cu

(n - (m+n)y)² (n+1 - (m+n+2)y)( n - (m+n)y) + (m+n)y(1 - y) 0 < y <

care, in urma reducerii termenilor asemenea devine

(m+n)y² - 2ny + n

care este evidenta: discriminantul D = n² - n(m+n) este negativ.

Observatie. Din inegalitatile 5.4, 5.6 si (5.9) rezulta urmatoarele estimari

r_Gamma(p+1,1)(x)

r_N (x) x₊

r_{Beta(m+1,n+1)}(x)

Mai mult, in cazul in care p este un numar natural, prima inegalitate din (5.13) devine chiar egalitate.

Ca exemplu de aplicare:

p T r_Gamma(p+1,1)(x)

1 < p T r_Gamma(p+1,1)(x)

In legatura cu (5.13), ar fi de verificat numai ca r_Gamma(p+1,1)(x) 1 ceea ce este acelasi lucru cu x^pe^-x care este evidenta : t x T = x^p = x^pe ^-x . Cit despre (5.14), inegalitatea r' 0 este echivalenta cu .

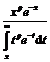
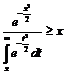
Se poate arata chiar mai mult: functia r_N(0,1) este chiar convexa si pentru x mare r_N(0,1)(x) x. (Vezi de exemplu Gnedenko, Beleaev, Soloviev , pg. 104). Demonstratia nu este de loc simpla.

Familiile de repartitii uzuale de tip IFR au anumite proprietati de monotonie. Sa spunem ca o familie de repartitii (m_t)_{t I I R} este crescatoare(respectiv descrescatoare )daca s < t T m_{s m} m_t si (respectiv s < t T m_{t m} m_s

PROPOZITIA 5.5.

(i). Familia (Binomial (n,p))_{n I N p} este crescatoare atit in n cit si in p;

(ii). Familia (Negbin(n,p)) _{n I N p} este crescatoare in n si descrescatoare in p ;

(iii). Familia (Poisson(l _l este crescatoare;

(iv). Familia (Uniform(0,a))_a este crescatoare;

(v). Familia (Gamma(n+1,a))_{n, a} este crescatoare in n si descrescatoare in a;

(vi). Familia (Beta(m+1, n+1))_{m, n} este crescatoare im m si descrescatoare in n;

(vii). Familia (N(m s _{mI R s} este crescatoare in m, nu are monotonie in s

Demonstratie.(i).: Este suficient de verificat ca p < q T Binomial(1, p) _m Binomial(1, q) si apoi aplicam Teorema 4.5; (ii).: Este suficient de verificat ca p < q T Negbin(1, q) _m Negbin(1, p) ceea ce este iarasi evident: repartitia binomial negativa este in acest caz repartitia geometrica, avind rata de defectare constanta: r_Negbin(1,q) = q > p = r_Negbin(1,p) ; (iii).: Poisson(l) = lim_n Binomial(n, ). Aplicam punctul (i). si invarianta relatiei " _m" la convergenta slaba.

(iv). Este imediat caci r_Uniform(0,a)(x) = 1_(0,a)(x);

(v). Fie 0 < a < b . Atunci, din propozitia 2.2 avem relatiile

r : = r_Gamma(n+1,a)(x) = ar_Gamma(n (ax), r₂ := r_Gamma(n+1,b)(x) = br_Gamma(n (bx) . Trebuie aratat ca r₁ r₂ , sau ceea ce este imediat deoarece a < b T ax < bx T r_Gamma(n (ax) r_Gamma(n (bx) (caci repartitiile Gamma sunt de tip IFR!) T . Deci aplicatia a a Gamma(n+1,a) este descrescatoare. Pentru a demonstra cealalta monotonie, observam ca datorita invariantei la operatia de scalare este suficient de aratat ca m < n T Gamma(m+1, 1) _m Gamma(n+1, 1) sau ca

x > 0 T

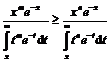
care este echivalenta cu

= x^n-m

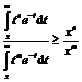
ceea ce este imediat: (caci t x !) .

(vi). Demonstratia este asemanatoare cu cea a punctului precedent : daca m < m' atunci deci r_{Beta(m, n)}(x) r_{Beta(m', n)}(x) iar daca n < n' atunci deci r_{Beta(m, n)}(x) r_{Beta(m, n')}(x) .

(vii). Rezulta imediat din relatia : intr-adevar, m < m T x - m x - m T T .

Faptul ca N(m s ) si N(m s'²) nu sunt comparabile este clar deoarece cele doua repartitii au aceiasi medie, m. Daca, sa zicem N(m s _m N(m s'²) atunci ar trebui ca N(m s _st N(m s'²) deci functiile de supravietuire sa fie comparabile, ceea ce nu este adevarat caci ambele functii au graficul simetric fata de punctul (m

Proprietati ale repartitiilor de tip "IFR"

Vom folosi notatiile de la paragraful 2: F_T(x) = P(T x) = e^-R(x)

Faptul ca logaritmul functiei de supravietuire este o functie concava are consecinte.

In primul rind toate repartitiile de tip IFR pozitive au momente de orice ordin.

PROPOZITIA 6.1. Fie T I IFR o variabila aleatoare pozitiva. Atunci T I L^p p <

Analogul discret este de asemenea adevarat: daca T I IFR(1) atunci ET^p < p

Demonstratie. Daca T este marginita, nu este nimic de demonstrat. Daca nu, fiind de tip IFR, variabila aleatoare T este absolut continua, deci R este de forma R(x) = dt unde r este riscul instantaneu de moarte. Mai mult, functia r : [0, ] este crescatoare si exista x₀ ca a:=r(x₀)>0. Deci x x₀ T R(x) dt = r(x₀)(x - x₀) = a(x-x₀) T F(x) . Daca x < x₀ inegalitatea este cu atit mai mult adevarata, deci avem estimarea F(x) Ce^-ax T ET^p = dt dt <

Daca T I IFR(1) atunci logF nu mai este concava. Avem doua situatii: sau T este marginita - deci nu mai este nimic de demonstrat- sau sirul (R_n)_n = (logF(n))_n este concav. Unind cu segmente de dreapta punctele (n,R_n) si (n+1,R_n+1) obtinem o functie poligonala concava, R*, avind proprietatea ca F e^-R* si demonstratia este analoga: ET^p = dt e^{-R* (t)}dt <

Observatie. Sa presupunem ca T este o variabila aleatoare nemarginita cu valori naturale. Daca notam F* = e^{- R*} obtinem tot o functie de supravietuire, a unei variabile aleatoare T* care este absolut continua de data aceasta, de tip IFR, si domina stocastic pe T. Am putea numi variabila T* aproximarea IFR a lui T. Daca T este marginita, fie k primul n cu proprietatea ca F(n) = 0. Operatia de inlocuire a lui -R cu o linie poligonala - R* situata deasupra lui R nu se mai poate face decat pina la acest n; variabila aleatoare T* de care vorbeam nu mai este absolut continua, ci repartitia sa este o mixtura intre o repartitie absolut continua si e_n-

In al doilea rind, in cazul repartitiilor de tip IFR functia F este log - concava, lucru care nu poate ramine fara urmari.

PROPOZITIA 6.2. Fie T 0 o variabila aleatoare pozitiva de tip IFR cu functia de supravietuire F si fie m = ET > 0.. Atunci

0 < x < m T F(x)

Demonstratie. Functia g(x) = log F(x) este concava. Inegalitatea Jensen spune atunci ca

Eg(T) g(ET) = g(m

Fie X = F(T). Daca T ar fi continua, X ar fi uniform repartizata.

In general, fie a = inf F > 0 , b = sup F < 1

Avem doua cazuri.

Cazul 1. Daca b < , deci T I L , fie p = F(b) = P(T b) = P(T = b). Functia F : (a,b) (p,1) este continua si strict descrescatoare (este continua deoarece logF este concava, deci continua si strict descrescatoare deoarece daca ar exista a < x₁ < x₂ < b ca g(x₁) = g(x₂) ar trebui ca g(x) sa coincida cu g(x₁) pentru orice x I (x₁, x₂), ceea ce ar contrazice concavitatea functiei g). Inseamna ca F este bijectiva pe (a,b) si are o inversa F^-1: (p,1) (a,b).

Calculam functia de repartitie a variabilei aleatoare X. Avem doua cazuri:

daca p < x < 1 atunci P(X x) = P(F(T) x) = P(F(T) F(F ^-1(x))) = P(T F ^-1(x)) = F(F ^-1(x)) = x.

Daca 0 < x < p atunci P(X x) = 0, deoarece p X 1 (a.s.)

In concluzie functia de repartitie a variabilei aleatoare X este F_X(x) = x1_[p,1](x) + 1_(1, (x) ceea ce corespunde repartitiei P X^- = pe_p + (1-p)U(p,1). Ca atare in acest caz avem

Eg(T) = ElogX = plog p + x dx = - ( 1 - p) > - 1

Cazul 2. Daca b = este cazul simplu, deoarece atunci T este o variabila absolut continua, p = F(b) = 0 si X este uniform repartizata. Deci acum

Eg(T) = ElogX = x dx = - 1 = - 1 + p

Inlocuind in (6.2) deducem ca in ambele situatii log F(m - 1 deci ca

F(m) = P(T ET) e ^{-1+ p}

Pe de alta parte functia t a g(t)/t ( = !) este descrescatoare - asa e la functii concave, asadar si functia t a este descrescatoare. Deci daca t < m atunci (din 6.4). Acum inegalitatea (6.1) este evidenta.

Propozitia 6.2 sugereaza ca, in cazul repartitiilor IFR continue macar, putem spune cite ceva despre cuantile. Fie T o variabila aleatoare de tip IFR absolut continua avind functia de repartitie F si cea de supravietuire F, p I (0,1) si x(p) = sup t F(t) p - cuantila de ordin p . Din continuitatea functiilor F si F avem atunci ca (6.1) F(x(p)) = p, F(x(p)) = 1 - p si - R(x(p)) = log(1-p)

Fie - a = . Functia -R fiind concava, sunt valabile inegalitatile

t x(p) T F(t) e^{- at}, t > x(p) T F(t) e^-at

PROPOZITIA 6.3. Fie T o variabila aleatoare de tip IFR absolut continua cu functia de repartitia F si cea de supravietuire F , fie m = ET si M = Median(T). Atunci

x(p)

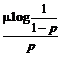
mlog2 M m log2

Daca T nu este absolut continua, inseamna ca este esential marginita. Atunci estimarile de mai sus se pot imbunatati astfel

x(p) p I ( 0, F( ))

M m log2)

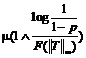
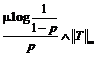
Demonstratie. Daca T este absolut continua, F( ) = 0. Sa presupunem ca x(p) m. Inlocuind in (6.1) deducem ca F(x(p)) . Dar F este continua, deci F(x(p)) = 1 - p ; asadar log(1-p) x(p)/m . Altfel spus am verificat ca ca

x(p) m T x(p)

Daca x(p) m nu e nimic de demonstrat caci m Astfel am demonstrat prima inegalitate din (6.6).

Pe de alta parte functia am vazut ca functia t a -R(t)/t este descrescatoare deci F(t)^{1/ t} este de asemenea descrescatoare. Avem atunci inegalitatile

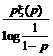
m 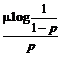= dt dt = dt dt = dt (cu A = ) = = (caci A^x(p) = F(x(p)) = 1 - p !) de unde x(p) Am demonstrat astfel a doua inegalitate (6.6)..

Inegalitatea 6.7 rezulta inlocuind p cu ½ : mediana este cuantila la 50%.

In fine, daca T nu este absolut continua (deci marginita esential) , aplicam din nou inegalitatea (6.1) care spune ca x(p) < m T F x(p)) log(1 - p) = de unde rezulta prima estimare din (6.6'); a doua este evidenta, toate cuantilele sunt mai mici ca supremul esential.

Observatie. Dupa cum ne putem convinge studiind mediana unei variabile aleatoare de tipul X = Y m unde Y ~ U(0,1) sau Y ~ e₁ , cele doua margini din (6.7') se ating. Adica inegalitatea nu poate fi substantial imbunatatita.

Observatie. Inegalitatea (6.4) F (ET) e^-1 nu are nici un analog discret. De exemplu, daca T ~ Binomial(n,p) cu p suficient de mic, F(ET) = F(np) = np poate fi facut oricit de mic; daca T ~ Poisson(l) cu l < 1 atunci F(ET) = F(l) = (1 - e ^{- l} l poate fi de asemenea oricit de mic.

Pentru a obtine estimari de cuantile in cazul variabilelor aleatoare discrete vom folosi "aproximatia IFR" a lor.

Fie T o variabila aleatoare cu valori naturale, p_n = P(T = n), F_n = P(T n) si m = ║T║ = max n F_n - care poate sa fie si . Unim punctele de coordonate (n,logF_n) si (n+1,logF_n+1) cu segmente de dreapta pentru n = 0,1,., m-1 si obtinem astfel graficul unei functii concava pe [0,m) situata deasupra graficului functiei logF ; sa notam aceasta functie cu - R* . Fie F*(x) = e ^{- R*(x)}1_[0,m](x) (daca m ) sau F*(x) = e ^{- R*(x)} (daca m = ) . Atunci F* este functia de supravietuire a unei variabile aleatoare T* care este de tip IFR; mai mult, T p_st T* caci T* are functia de supravietuire mai mare.

Mai mult, daca analizam cele doua functii, F si F* vedem ca

F*(x+1) F(x) F*(x)

ceea ce ne va permite sa dam estimari de cuantile.

Fie m = ET = (x) dx si m* = ET* = *(x) dx . Din (6.9) deducem ca

m m m

Intr-adevar, ca m m* este evident. A doua inegalitate rezulta integrind prima inegalitate din (6.9): deci *(x+1)dx (x) dx deci , (cu t = x+1) *(t)dt - *(t)dt m T m*- *(t)dt m de unde m m *(t)dt

Fie x(p) cuantilele lui T si x*(p) cuantilele lui T* . Din (6.9) deducem clestele

x*(p) - 1 x(p) x*(p)

Acum putem aplica estimatiile din Propozitia 6.3.

PROPOZITIA 6.4. Fie T I IFR(1) o variabila aleatoare cu valori naturale, b = ║T║ , F functia sa de supravietuire, F functia de repartitie, a = F(b) = 1 - F(b), m = ET, x(p) cuantilele sale. Atunci

- 1 x(p) p I a

- 1 Median(T) m 2log2) b

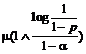
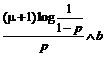
Demonstratie. Se aplica (6.11), (6.10) si inegalitatile (6.6') si (6.7').

Bibliografie

1. Gnedenko, B., Beliaev Y., Soloviev A. , Methodes Mathematiques dans la Theorie de la Fiabilite, Mir 1972;

2. Barlow, R. E., and F. Proschan. Mathematical Theory of Reliability. J. Wiley & Sons. (1965)

Reprinted (1996) SIAM, Philadelphia, PA.

3. Goovaerts, M.J., Kaas, R., Van Herwaarden, A. E., Bauwelinckx T.: Effective actuarial methods, North Holland 1990

4. Burlacu, V., Cenusa Gh., Bazele matematice ale teoriei asigurarilor, Bucuresti 2000