MINISTERUL EDUCATIEI, CERCETARII  SI INOVARII

INSPECTORATUL SCOLAR JUDETEAN IASI

LICEUL DE INFORMATICA „GRIGORE T. MOISIL” IASI

CONCURSUL DE MATEMATICA FLORICA T. CAMPAN

ETAPA INTERJUDETEANA, 21 MARTIE

SOLUTII SI BAREME

Clasa a VII-a

1.Luandu-se dupa harta care a apartinut piratului Supernegru, pentru a gasi comoara fabuloasa (adica o supercomoara) ascunsa de acesta candva, undeva in Caraibe, patru supercautatori trebuie sa caute in interiorului patrulaterului NESV situat pe un teren plat si obtinut astfel: din acelasi punct O, fiecare dintre cei 4 merge, in linie dreapta, primul face b pasi spre nord pana in N, al doilea c pasi spre est pana in E, al treilea a pasi spre sud pana in S si ultimul a pasi spre vest pana in V (a,b,c numere naturale). Stiind ca intre N si E sunt exact a pasi si ca lungimea pasului fiecaruia dintre cei 4 este aceeasi si constanta, aratati ca suprafata patrulaterului NESV are aria exprimata printr-un numar natural (unitatea de masura este patratul cu latura de 1pas). Este posibil ca aria patrulaterului sa fie egala cu aria unui patrat de latura 6 pasi ?

Solutie

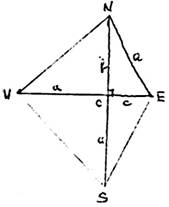I Observam ca , deci ; cum cel putin unul dintre numerele si este numar par. Sa presupunem, prin reducere la absurd, ca si sunt ambele impare si sa mai observam ca . Daca presupunem ca a este impar, atunci b si c trebuie sa fie, ambele, pare, de unde si sunt pare si din par, adica a par, contradictie. Daca a este par, atunci b si c trebuie sa fie ambele impare.

a par multiplu de 4; fie si , atunci , adica este multiplu de 4 plus 2. Cum este adevarata, ajungem la o contradictie. Ramane ca, macar unul dintre numerele , este par.

II si deci este multiplu de 4 este multiplu de 2

Barem

Modeleaza geometric situatia descrisa de problema: patrulaterul NESV este ortodiagonal cu lungimile diagonalelor si … 2

. . . . . . . . . . . . . 1

.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 1

Presupune, prin R.A. ca  si sunt ambele impare .. . . . . . . . . . . . 1

Daca a impar, arata ca se ajunge la o contradictie .. . . . . . . . . . . . . ..  3

Daca a par, arata ca se ajunge la o contradictie .. . . . . . . . . . . . . . ..  4

Finalizare .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..  1

2.i) Fie numere reale pozitive. Demonstrati ca este media geometrica a lui si daca si numai daca

ii) Fie punctul de intersectie a diagonalelor patrulaterului convex. Demonstrati ca daca si numai daca

Solutie

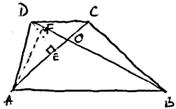i)

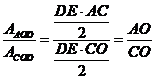ii)Notam si si observam ca si Conform i) avem (1). Fie si , , .

si 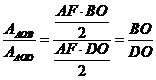acum (1) , q.e.d.

Barem

i) aducerea corecta la acelasi numitor .. . . . . . . . . . . . . . . . . . . . . 1p

.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2p

ii)  observa ca se poate folosi i) si arata ca 3p

arata ca si .. . . . . . . . . . . . . . . . . . . .. 3p

.. . . . . . . . . . . . . . . . . . . . . 2p

3p

3. Rezolvati in multimea numerelor intregi ecuatia:

Solutie

Notam si .. . . . . . .. . .. . . . . .. .. . . . . .. .. . . . . .. .. . . . .. 1p

Ecuatia devine .. . . . . .. .. . . . . .. .. . . . . .. .. . . . . .. 1p

Grupand convenabil, obtinem .. . . . . .. .. . . . . .. .. . . . . .. 4p

Rezulta .. . . . . .. .. . . . . .. .. . . . . .. .. . . . . .. .. . . . .. 2p

Apar urmatoarele patru posibilitati

sau sau sau ………….………….………….……….. 2p

Numai primul si ultimul au solutii intregi: (0,1),(1,0),(-6,1),(,-6) .. . .. .. . .. .. . .. .. . .. .. . . 1p

Prin urmare solutiile ecuatiei sunt …….. . . . . . . . . . . 2p