 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
Siruri de numere reale. Puncte limita. Convergenta
Definitia 1.1.1. Fie sirul ![]() de numere reale. Un
numar real a se numeste punct
limita al sirului considerat, daca in orice
vecinatate a sa se afla o infinitate de termeni ai sirului.
de numere reale. Un
numar real a se numeste punct
limita al sirului considerat, daca in orice
vecinatate a sa se afla o infinitate de termeni ai sirului.
Notandu-se
cu L multimea punctelor limita
pentru sirul ![]() , marginea superioara a multimii L se va numi limita superioara a
sirului, iar marginea inferioara a multimii L se va numi limita inferioara a
sirului considerat.
, marginea superioara a multimii L se va numi limita superioara a
sirului, iar marginea inferioara a multimii L se va numi limita inferioara a
sirului considerat.
Se
va scrie: ![]() si
si ![]() .
.
Sirul cu termenul general 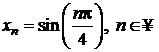 , are ca puncte limita pe
, are ca puncte limita pe 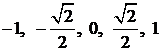 .
.
Sirul cu termenul general ![]() , va avea
, va avea ![]() , deci
, deci ![]() , sirul fiind convergent.
, sirul fiind convergent.
Definitia 1.1.2. Sirul ![]() se numeste convergent,
daca exista un numar x,
astfel incat pentru
se numeste convergent,
daca exista un numar x,
astfel incat pentru ![]() , astfel incat pentru
, astfel incat pentru ![]() sa se verifice
sa se verifice ![]() .
.
Numarul
real x cu proprietatea de mai sus se
numeste limita sirului ![]() si se va scrie
si se va scrie ![]() .
.
Daca
un sir ![]() este convergent,
limitele sale superioara si inferioara sunt egale.
este convergent,
limitele sale superioara si inferioara sunt egale.
Definitia 1.1.3. Un sir care are limita infinita sau un sir pentru care cele doua limite, inferioara si superioara, sunt diferite se numeste sir divergent.
Teorema lui Weierstrass Orice sir monoton si marginit este convergent.
Teorema
Töplitz. Fie o matrice infinita de numere reale ![]() cu proprietatea
ca exista
cu proprietatea
ca exista ![]() , astfel incat:
, astfel incat:
![]() .
.
Urmatoarele afirmatii sunt echivalente:
pentru orice sir convergent de numere reale ![]() sirul
sirul ![]() definit prin
definit prin 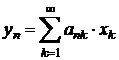 este convergent
si
este convergent
si ![]() ;
;
(i) ![]() ;
;
(ii)
![]() .
.
Consecinta 1. Daca in Teorema
Töplitz se modifica punctul 2) (ii) in ![]() , atunci afirmatia 1) devine
, atunci afirmatia 1) devine ![]() .
.
Teorema Cesaro-Stolz Fie
sirul ![]() oarecare si
oarecare si ![]() monoton crescator
de numere pozitive, cu
monoton crescator
de numere pozitive, cu ![]() . Atunci, daca exista
. Atunci, daca exista 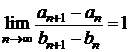 , va exista si
, va exista si 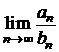 si cele doua
limite vor avea aceeasi valoare.
si cele doua
limite vor avea aceeasi valoare.
Se aplica Teorema Töplitz
sirului 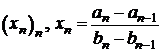 , iar sirul dublu
, iar sirul dublu
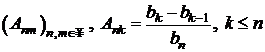 si
si ![]() .
.
In aceste conditii 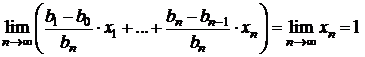 .
.
De asemenea, 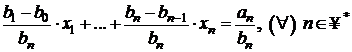 .
.
Consecinta 2. Daca 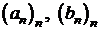 sunt doua
siruri de numere reale cu proprietatile:
sunt doua
siruri de numere reale cu proprietatile:
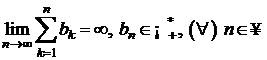 ;
;
![]() .
.
Atunci 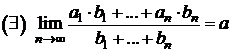 .
.
Criteriul radicalului
Daca sirul ![]() este convergent
si are termenii pozitivi, atunci
este convergent
si are termenii pozitivi, atunci ![]() .
.
Se aplica teorema Cesaro-Stolz pentru
sirurile ![]() si
si ![]() . Atunci
. Atunci
![]() ,
,
de unde rezulta ![]() si de aici
cerinta problemei.
si de aici
cerinta problemei.
Criteriul raportului
Daca sirul ![]() are termenii pozitivi,
atunci
are termenii pozitivi,
atunci 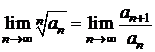 , daca ultima limita exista.
, daca ultima limita exista.
Criteriul majorarii
Daca ![]() si
si ![]() , atunci
, atunci ![]() .
.
O reciproca a teoremei Cesaro-Stolz
Daca 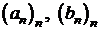 sunt doua
siruri de numere reale cu proprietatile:
sunt doua
siruri de numere reale cu proprietatile:
![]() ;
;
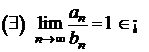 ;
;
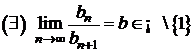 .
.
Atunci 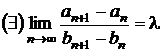 .
.
Criteriul general de convergenta al lui Cauchy. Conditia necesara
si suficienta ca un sir ![]() sa fie convergent
este ca pentru
sa fie convergent
este ca pentru ![]() ,
, ![]() , astfel incat pentru
, astfel incat pentru 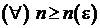 si pentru
si pentru ![]() sa se verifice
sa se verifice ![]() .
.
1.2 Siruri recurente
Definitia 1.2.1. Un sir ![]() se numeste sir
recurent daca este definit de o relatie de forma
se numeste sir
recurent daca este definit de o relatie de forma ![]() cunoscuti.
Numarul natural k se
numeste ordinul relatiei de recurenta.
cunoscuti.
Numarul natural k se
numeste ordinul relatiei de recurenta.
Recurenta de ordinul 1
![]() .
.
Cazul 1. ![]() .
.
Cazul 2. ![]() .
.
Cazul 3. ![]() .
.
Se cauta un sir cu
termenul general de forma ![]() .
.
![]() . Impunem conditia
. Impunem conditia ![]() si rezulta
si rezulta ![]() si deci
si deci
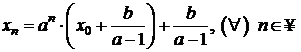 .
.
![]() .
.
Observatie. Printr-o
translatie a sirului ![]() se poate obtine o
recurenta de forma
se poate obtine o
recurenta de forma ![]() .
.
Pentru
aceasta problema se cauta solutii de forma ![]() . Inlocuind aceasta in relatia de recurenta,
vom obtine ecuatia
. Inlocuind aceasta in relatia de recurenta,
vom obtine ecuatia ![]() numita
ecuatia caracteristica asociata recurentei.
numita
ecuatia caracteristica asociata recurentei.
Se disting trei cazuri:
Cazul I: Daca ![]() , ecuatia caracteristica are doua
radacini reale si distincte
, ecuatia caracteristica are doua
radacini reale si distincte ![]() .
.
Lema 1. Sirurile cu termenii
generali ![]() , sunt solutii ale relatiei de recurenta.
, sunt solutii ale relatiei de recurenta.
Lema 2. Orice combinatie
liniara a sirurilor ![]() , este solutie a relatiei de recurenta.
, este solutie a relatiei de recurenta.
Lema 3. Solutia generala ![]() a relatiei de
recurenta si sirurile
a relatiei de
recurenta si sirurile ![]() ,
, ![]() sunt liniar
dependente.
sunt liniar
dependente.
Prin urmare, solutia generala a relatiei de recurenta este:
![]() .
.
Cazul II: Daca ![]()
Lema 1. Sirurile cu termenii
generali ![]() sunt solutii ale
relatiei de recurenta.
sunt solutii ale
relatiei de recurenta.
Lema 2. Orice combinatie
liniara a sirurilor ![]() este solutie a
relatiei de recurenta.
este solutie a
relatiei de recurenta.
Lema 3. Solutia generala ![]() a relatiei de
recurenta si sirurile
a relatiei de
recurenta si sirurile ![]() ,
, ![]() sunt liniar
dependente.
sunt liniar
dependente.
Prin urmare, solutia generala a relatiei de recurenta este:
![]() .
.
Cazul III: Daca ![]() .
.
Lema 1. Sirurile cu termenii
generali ![]() si
si ![]() sunt solutii ale
relatiei de recurenta.
sunt solutii ale
relatiei de recurenta.
Lema 2. Orice combinatie
liniara a sirurilor ![]() este solutie a
relatiei de recurenta.
este solutie a
relatiei de recurenta.
Lema 3. Solutia generala ![]() a relatiei de
recurenta si sirurile
a relatiei de
recurenta si sirurile ![]() ,
, ![]() sunt liniar
dependente.
sunt liniar
dependente.
Prin urmare, solutia generala a relatiei de recurenta este:
![]() .
.
Observatie. Pentru relatii de recurenta de ordin superior lui doi se procedeaza similar, urmand urmatoarele etape:
se scrie si se rezolva ecuatia caracteristica;
se scrie solutia generala a relatiei de recurenta ca o combinatie liniara a solutiilor partiale.
1.3
Siruri in ![]()
Fie 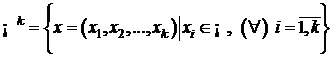 . Elementele lui
. Elementele lui ![]() se numesc puncte
sau vectori.
se numesc puncte
sau vectori.
Observatie. Pe multimea ![]() se definesc
operatiile de adunare si inmultire cu numere reale prin
se definesc
operatiile de adunare si inmultire cu numere reale prin
![]()
![]() .
.
![]() are o structura de
spatiu vectorial peste corpul K.
are o structura de
spatiu vectorial peste corpul K.
Definitia 1.3.1. Fie ![]() . O aplicatie
. O aplicatie ![]() se numeste produs
scalar pe multimea X,
daca
se numeste produs
scalar pe multimea X,
daca
![]()
![]()
![]()
![]() , unde
, unde ![]() este conjugatul
numarului complex
este conjugatul
numarului complex ![]() .
.
Pentru ![]() conditia 4) din
definitia produsului scalar devine
conditia 4) din
definitia produsului scalar devine ![]() .
.
Observatie. Pe spatiul vectorial ![]() se introduce
produsul scalar de forma
se introduce
produsul scalar de forma 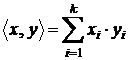 .
.
Definitia 1.3.2. Fie ![]() . O aplicatie
. O aplicatie ![]() se numeste norma
pe X, daca
se numeste norma
pe X, daca
![]()
![]()
![]() .
.
Rezulta
ca ![]() .
.
Definitia 1.3.3. Fie ![]() si
si ![]() . Multimea punctelor
. Multimea punctelor ![]() pentru care
pentru care ![]() se numeste sfera
deschisa cu centrul in a
si de raza r.
se numeste sfera
deschisa cu centrul in a
si de raza r.
Definitia 1.3.4. Fie ![]() si
si ![]() . Multimea punctelor
. Multimea punctelor ![]() pentru care
pentru care ![]() se numeste sfera
inchisa cu centrul in a
si de raza r.
se numeste sfera
inchisa cu centrul in a
si de raza r.
Observatie. In cazul in care ![]() sfera deschisa
devine multimea punctelor
sfera deschisa
devine multimea punctelor ![]() pentru care
pentru care ![]() .
.
Notatie.
Vom nota cu ![]() sfera cu centrul in a si raza r.
sfera cu centrul in a si raza r.
Definitia 1.3.5. Multimea ![]() se numeste deschisa,
daca pentru
se numeste deschisa,
daca pentru ![]() exista o
sfera deschisa
exista o
sfera deschisa ![]() .
.
Exemplu
Intervalele
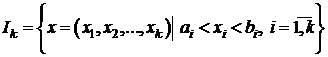 sunt multimi
deschise in
sunt multimi
deschise in ![]() .
.
Definitia 1.3.6. Fie ![]() . O multime
. O multime ![]() se numeste vecinatate
a punctului a, daca exista
o multime deschisa inclusa in V si care-l contine pe a.
se numeste vecinatate
a punctului a, daca exista
o multime deschisa inclusa in V si care-l contine pe a.
Notatie.
Vom nota cu ![]() multimea tuturor
vecinatatilor lui a.
multimea tuturor
vecinatatilor lui a.
Definitia 1.3.7. Fie ![]() . Un punct a se
numeste punct de acumulare pentru A,
daca
. Un punct a se
numeste punct de acumulare pentru A,
daca ![]() verifica
verifica ![]() .
.
Definitia 1.3.8. Se numeste sir in ![]() ,
, ![]() , o
aplicatie
, o
aplicatie ![]() , definita prin
, definita prin ![]() , unde
, unde ![]() .
.
Notatie ![]() .
.
Sirul 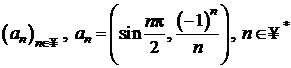 este din
este din ![]() .
.
Definitia 1.3.9. Sirul ![]() din
din ![]() este convergent,
daca exista
este convergent,
daca exista ![]() , astfel incat
, astfel incat ![]() pentru care
pentru care ![]() ,
, ![]() .
.
Observatie. Pentru ![]() avem
avem
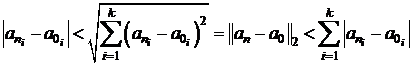 .
.
Din aceste inegalitati
rezulta ca un sir din ![]() este convergent
daca si numai daca sirurile componente
este convergent
daca si numai daca sirurile componente ![]() , sunt convergente in
, sunt convergente in ![]() .
.
Definitia 1.3.10. Sirul ![]() din
din ![]() se numeste sir
Cauchy daca pentru
se numeste sir
Cauchy daca pentru ![]() , astfel incat pentru
, astfel incat pentru 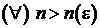 si pentru
si pentru ![]() sa avem
sa avem ![]() .
.
Teorema 1.3.11. Conditia necesara
si suficienta ca un sir ![]() din
din ![]() sa fie convergent
este ca el sa fie sir Cauchy.
sa fie convergent
este ca el sa fie sir Cauchy.
1.4 Aplicatii
Sa se determine punctele limita pentru urmatoarele siruri:
a) ![]() ; b)
; b) 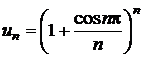 ; c)
; c) ![]() ;
;
d) ![]() e)
e) ![]() .
.
a)
pentru n numar par,
![]() ; pentru n
numar impar
; pentru n
numar impar ![]() ; deci, punctele limita sunt a si
; deci, punctele limita sunt a si ![]() ;
;
b)
e si ![]() ;
;
c)
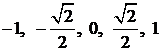 ;
;
d)
![]() ;
;
e)
pentru ![]() avem
avem ![]() , deci
, deci ![]() . Pentru
. Pentru ![]() avem
avem ![]() , deci
, deci ![]() . Se obtin punctele limita 2 si 0.
. Se obtin punctele limita 2 si 0.
Sa se determine limitele inferioara si superioara pentru urmatoarele siruri
a)
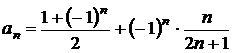 ;
;
b)
![]() ;
;
c)
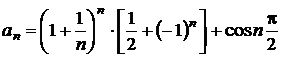 .
.
a)
se determina punctele limita ale sirului; pentru n numar par ![]() , iar pentru n
numar impar
, iar pentru n
numar impar ![]() ; deci, multimea punctelor limita este
; deci, multimea punctelor limita este 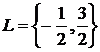 , de unde rezulta ca
, de unde rezulta ca 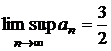 si
si ![]() ;
;
b)
![]() si
si ![]() ;
;
c)
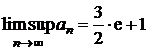 si
si ![]() .
.
Folosind teorema lui Weierstrass sa se studieze convergenta urmatoarelor siruri:
a) 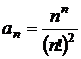 ; b)
; b) ![]() ;
;
c) 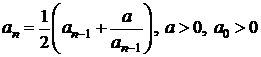 ; d)
; d) 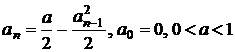 ;
;
e) ![]() ; f)
; f) 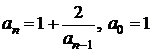
g) ![]() .
.
a)
sirul ![]() este cu termeni
pozitivi, iar raportul
este cu termeni
pozitivi, iar raportul
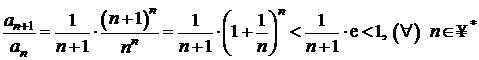 ,
,
de unde rezulta ca sirul este monoton descrescator. Cum toti termenii sunt pozitivi, sirul va fi marginit inferior de 0, deci este convergent.
Pentru calculul limitei, daca
![]() , introducand limita in relatia de recurenta
, introducand limita in relatia de recurenta 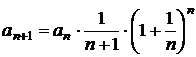 , se va obtine
, se va obtine ![]() , de unde
, de unde ![]() ;
;
b)
sirul ![]() este un sir de
numere pozitive si monoton crescator, demonstratie ce se poate
realiza prin inductie matematica dupa n. Presupunand ca ar exista
este un sir de
numere pozitive si monoton crescator, demonstratie ce se poate
realiza prin inductie matematica dupa n. Presupunand ca ar exista ![]() , aceasta va trebui sa verifice relatia de
recurenta, adica
, aceasta va trebui sa verifice relatia de
recurenta, adica ![]() , de unde
, de unde ![]() si se obtin
si se obtin 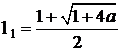 ,
, 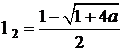 . Cum
. Cum ![]() nu convine, termenii
sirului fiind pozitivi, rezulta ca limita posibila
nu convine, termenii
sirului fiind pozitivi, rezulta ca limita posibila ![]() . Cum sirul este crescator, adica
. Cum sirul este crescator, adica ![]() si
si ![]() ,
, ![]() ,
, ![]() , rezulta
, rezulta 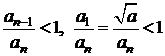 , de unde
, de unde 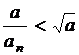 .
.
Din
relatia de recurenta ridicata la patrat se va
obtine ![]() , adica
, adica 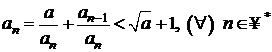 , adica sirul este marginit superior, deci
este convergent, iar
, adica sirul este marginit superior, deci
este convergent, iar ![]() este limita sa;
este limita sa;
c) convergent;
d) convergent;
e) convergent;
f)
cum ![]() rezulta ca
rezulta ca ![]() si
si 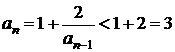 , deci sirul este marginit.
, deci sirul este marginit.
Pentru studiul monotoniei, se considera
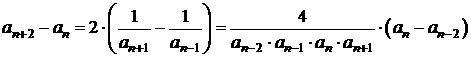 ,
,
deci ![]() are acelasi semn
cu
are acelasi semn
cu ![]() .
.
Deoarece
![]() , rezulta ca subsirul
, rezulta ca subsirul ![]() este monoton
crescator. Similar, deoarece
este monoton
crescator. Similar, deoarece ![]() , subsirul
, subsirul ![]() este
descrescator.
este
descrescator.
Cum
ambele subsiruri sunt si marginite rezulta ca
exista limitele lor, de forma ![]() .
.
In
acelasi timp 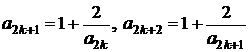 . Trecand la limita in cele doua relatii de
recurenta, obtinem
. Trecand la limita in cele doua relatii de
recurenta, obtinem 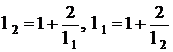 , echivalent cu
, echivalent cu ![]() . Daca
. Daca ![]() , rezulta ca
, rezulta ca ![]() , adica
, adica ![]() , ceea ce este fals. Rezulta
, ceea ce este fals. Rezulta ![]() , deci sirul este convergent;
, deci sirul este convergent;
g)
![]() . In continuare se demonstreaza prin inductie
matematica
. In continuare se demonstreaza prin inductie
matematica ![]() , deci putem scrie
, deci putem scrie ![]() . Rezulta ca exista
. Rezulta ca exista ![]() si
si ![]() si trecand la
limita in relatiile de recurenta, obtinem
si trecand la
limita in relatiile de recurenta, obtinem ![]() .
.
Folosind teorema Cesaro-Stolz, sa se calculeze urmatoarele limite:
a) ![]() ; b)
; b) 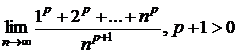 ; c)
; c) 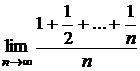 ;
;
d) 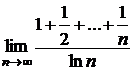 ; e)
; e) 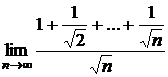 ;
;
f) 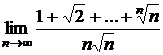 ; g)
; g) 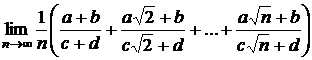 .
.
a)
Cu notatiile din teorema Cesaro-Stolz se considera ![]() , de unde rezulta
, de unde rezulta ![]() ;
;
b)
![]()
c)
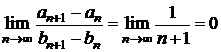 ;
;
d)
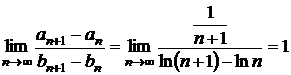 ;
;
e)
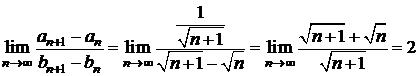 ;
;
f)
g)
![]() .
.
Sa se calculeze limitele urmatoare:
a) ![]() ; b)
; b) ![]() ; c)
; c) 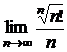 ;
;
a)
![]() ;
;
b)
![]() ;
;
c)
![]() ;
;
Fie ![]() un sir de numere
pozitive, crescator si divergent.
un sir de numere
pozitive, crescator si divergent.
a)
Sa se arate ca daca 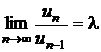 ,
, ![]() si
si 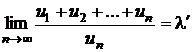 , atunci
, atunci ![]() .
.
b)
Sa se arate ca daca 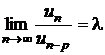 , unde
, unde ![]() , atunci
, atunci 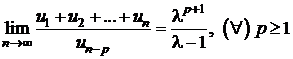 .
.
c)
Sa se arate ca daca 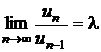 , unde
, unde ![]() , atunci
, atunci 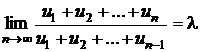 .
.
d)
Sa se arate ca daca 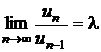 , unde
, unde ![]() , atunci
, atunci 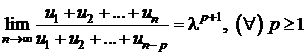 .
.
a)
se considera ![]() si se aplica
Teorema Cesaro-Stolz; rezulta
si se aplica
Teorema Cesaro-Stolz; rezulta
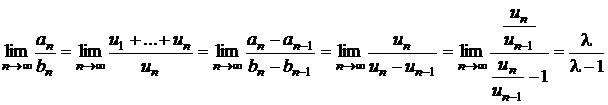 si deci
si deci ![]() ;
;
b)
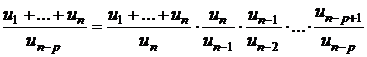 ;
;
rezulta
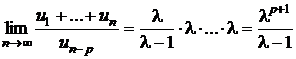 ;
;
c)
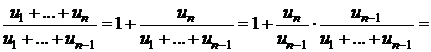
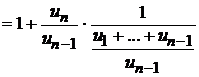 .
.
Trecand la limita si tinand seama de punctul b), se va obtine:
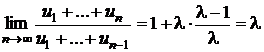 .
.
Utilizand criteriul general de convergenta al lui Cauchy, sa se demonstreze convergenta sirurilor:
a)
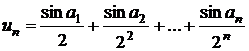 ;
;
b)
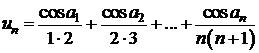 ;
;
c)
![]() ;
;
d)
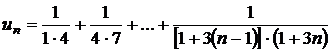 ;
;
e)
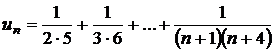 ;
;
f)
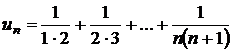 ;
;
g)
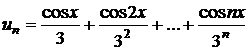 ;
;
h)
![]() .
.
a)
fiind dat ![]() arbitrar fixat, se va
cauta un rang
arbitrar fixat, se va
cauta un rang ![]() , astfel incat pentru
, astfel incat pentru 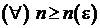 si pentru
si pentru ![]() sa se verifice
sa se verifice ![]()
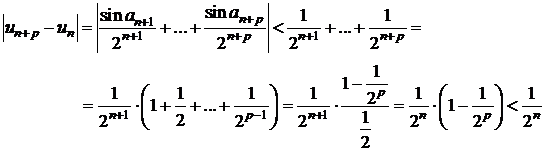
si cum ![]() se poate gasi un
rang, de exemplu
se poate gasi un
rang, de exemplu 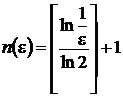 , pentru care
, pentru care ![]() , deci sirul este convergent;
, deci sirul este convergent;
c)
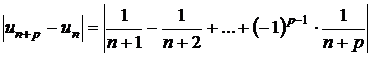 ; daca p este
numar par, atunci
; daca p este
numar par, atunci
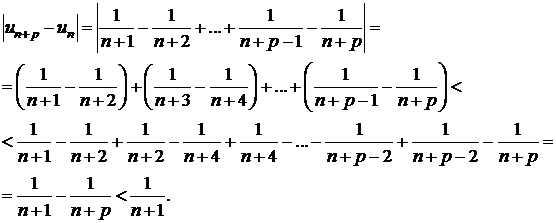
Daca p este impar, atunci
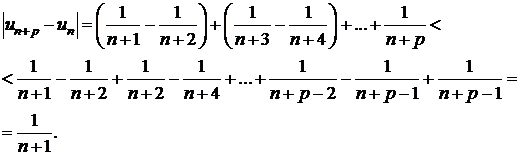
Cum ![]() , se poate gasi un rang
, se poate gasi un rang 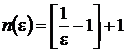 , pentru care
, pentru care ![]() , deci sirul este convergent;
, deci sirul este convergent;
d)
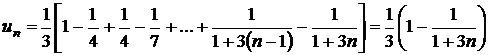 , de unde
, de unde 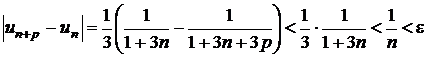 ;
;
e)
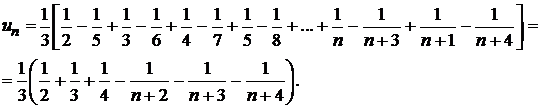
Rezulta 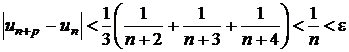 , deci sirul este convergent.
, deci sirul este convergent.
Se
considera sirul ![]() definit prin
relatia de recurenta:
definit prin
relatia de recurenta: ![]() fiind dati.
Sa se gaseasca expresia lui
fiind dati.
Sa se gaseasca expresia lui ![]() in functie de a, b
si
in functie de a, b
si ![]() . In acest caz exista
. In acest caz exista ![]() ?
?
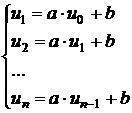 si inmultim
prima ecuatie cu
si inmultim
prima ecuatie cu ![]() , pe a doua cu
, pe a doua cu ![]() si asa mai
departe, ultima cu a. Prin adunare,
vom obtine:
si asa mai
departe, ultima cu a. Prin adunare,
vom obtine:
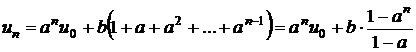 .
.
Daca ![]() ; deci,
; deci, ![]() nu are limita.
nu are limita.
Daca ![]() .
.
Daca ![]() ,
, ![]() , in functie de semnul lui b.
, in functie de semnul lui b.
Daca ![]() ,
, ![]() ,
, ![]() , sirul reducandu-se la doua puncte distincte, deci
nu are limita. Rezulta ca sirul are limita doar in
cazul
, sirul reducandu-se la doua puncte distincte, deci
nu are limita. Rezulta ca sirul are limita doar in
cazul ![]() .
.
Sa se studieze convergenta sirurilor:
a)
![]()
b)
![]() ;
;
c)
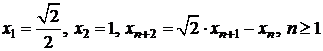 .
.
a)
ecuatia caracteristica este ![]() si se aplica
propozitia corespunzatoare cazului I; obtinem
si se aplica
propozitia corespunzatoare cazului I; obtinem ![]() si punand
conditiile
si punand
conditiile ![]() si
si ![]() , rezulta ca
, rezulta ca ![]() , care este divergent;
, care este divergent;
b)
ecuatia caracteristica este ![]() ; aplicandu-se propozitia corespunzatoare cazului
II, rezulta
; aplicandu-se propozitia corespunzatoare cazului
II, rezulta 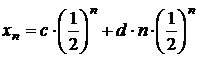 si punand
conditia ca
si punand
conditia ca ![]() , rezulta
, rezulta
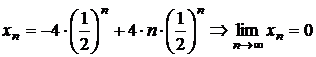 ;
;
c) divergent.
Fie ![]() si doua
siruri
si doua
siruri ![]() si
si ![]() definite prin:
definite prin:
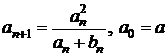 si
si 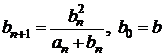 .
.
Sa se studieze ![]() si
si ![]() si sa se
deduca limitele celor doua siruri.
si sa se
deduca limitele celor doua siruri.
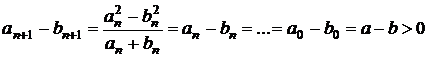 .
.
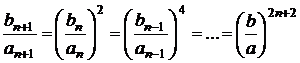 .
.
Cum ![]() , rezulta
, rezulta 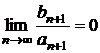 . In acelasi timp,
. In acelasi timp, 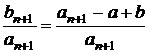 , deci
, deci 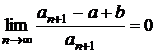 . Se va obtine astfel
. Se va obtine astfel ![]() si
si ![]() .
.
1.4.11 Se
considera sirurile ![]() si
si ![]() , care verifica urmatoarele conditii:
, care verifica urmatoarele conditii:
termenii sirului ![]() sunt pozitivi;
sunt pozitivi;
![]() are limita
infinita;
are limita
infinita;
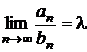 .
.
In
aceste conditii se verifica 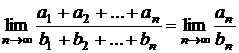 .
.
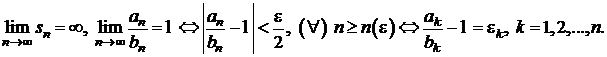
Rezulta ![]() . Luand
. Luand ![]() si insumand, se
va obtine
si insumand, se
va obtine
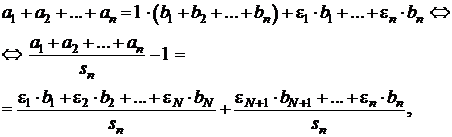
unde ![]() .
.
Atunci
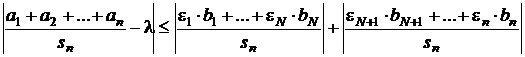 .
.
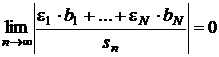 ,
,
iar
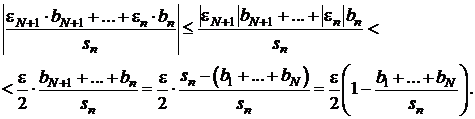
Rezulta 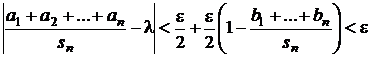 .
.
1.4.12 Sa
se arate ca daca ![]() si
si ![]() cu
cu ![]() are limita egala
cu b, atunci
are limita egala
cu b, atunci
![]() .
.
![]() ,
,
astfel incat pentru ![]() sa rezulte
sa rezulte ![]() .
.
De
asemenea, din ![]() rezulta ca
rezulta ca ![]() .
.
Cum
sirurile ![]() si
si ![]() sunt convergente, ele
sunt marginite, adica
sunt convergente, ele
sunt marginite, adica ![]() , astfel incat
, astfel incat ![]() ,
, ![]() si
si ![]() , astfel incat
, astfel incat ![]() .
.
Se
noteaza ![]() si
si ![]() si se
considera
si se
considera
![]() .
.
Atunci
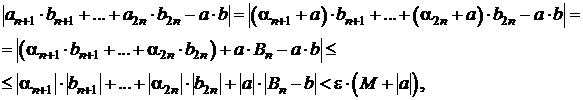
unde ![]() .
.
Rezulta
![]() .
.
TEST DE AUTOEVALUARE
Folosind criteriul lui Cauchy, sa se demonstreze divergenta sirurilor
a)
![]() ;
;
b)
![]() ; c)
; c) 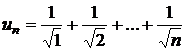 .
.
Sa se studieze convergenta sirurilor:
a)
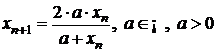 , cu
, cu ![]() ;
;
b)
![]()
c)
![]()
d)
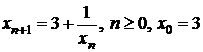 .
.
Sa se arate ca
sirul ![]() definit prin
definit prin
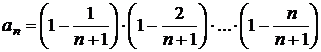
este convergent si sa se calculeze limita sa.
Sa se arate ca
sirul cu termenul general 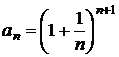 este convergent
si sa se deduca inegalitatea
este convergent
si sa se deduca inegalitatea 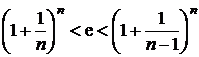 .
.
Sa se calculeze limitele urmatoare:
a) ![]() ;
;
b) 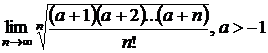 .
.
Copyright © 2026 - Toate drepturile rezervate