Combinari, combinari cu repetitie

Scopul lucrarii. Insusirea notiunile teoretice si practice legate de modul in care se abordeaza problemele care pot fi solutionate folosind:

combinarile de n elemente luate cite m,

sau combinarile cu repetitie de n elemente luate cite m.

Notiuni teoretice

2.1. Generarea combinarilor

Daca A este o multime cu n elemente, atunci submultimile lui A avind fiecare cite m elemente, unde 0 £ m £ n se numesc combinari de n elemente luate cite m.

Fie A, o multime cu n elemente si m < n. Ne intereseaza generarea tuturor celor C_n^m submultimi ale multimii A, care contin m elemente. O asemenea submultime se numeste m-combinare.

Pentru reprezentarea submultimii se va folosi reprezentarea printr-un vector cu n componente, fiecare continind un element al multimii. Deoarece in cadrul submultimii ordinea elementelor nu prezinta importanta, in vectorul v se vor genera toti cei C_n^m vectorii de forma v=(v₁, v₂, , v_m), ce satisfac relatiile: 1 £ v₁ < v₂ < .. < v_m £ n.

2.1.a. Algoritmul iterativ.

Generarea acestor vectori se face iterativ in ordine lexicografica. Astfel se pleaca de la vectorul v=(1, 2, , m) si se ajunge in final la vectorul (n-m+1, , n-1, n). Pentru a determina succesorul in ordine lexicografica a unui vector v=(v₁, v₂, , v_m) se procedeaza astfel:

a) se determina cel mai mare indice i care indeplineste conditia

v_i<n-m+i, v_i+1=n-m+i+1, , v_m-1=n-1, v_m=n;

b) se genereaza drept succesor urmatorul vector

(v₁, v₂, , v_i-1, v_i+1, , v_i+m-i+1).

Daca nu a fost gasit un indice i care sa respecte conditia de la a), inseamna ca vectorul v contine in ordine elementele n-m+1, n-m+2, , n-1, n, deci au fost generate toate cele C_n^m elemente.

In aceste conditii procedurile de initializare si generare sunt:

procedura INIT(v, n, m, ig) este

┌ pentru i=1, m, 1 repeta

│ v_i <- i

└

ig <- 1

sfarsit

procedura GEN(v, m, n, ig) este

gasit <- 0

i <- m

┌ cat_timp (i>0) si (gasit=0) repeta

│ ┌ daca v_i<n-m+i atunci

│ │ v_i <- v_i+1

│ │ ┌ pentru j=i+1, m, 1 repeta

│ │ │ v_j <- v_j-1+1

│ │ └

│ │ gasit <- 1

│ │altfel

│ │ i <- i-1

│ └

└

┌ daca gasit=0 atunci

│ ig <- 0

└

sfarsit

Pentru a evita cele 2 conditii (i>0) si (gasit=0) din procedura GEN, se poate folosi o variabila santinela pe pozitia 0 a vectorului v si care are valoarea diferita de n-m. In acest caz procedurile INIT si GEN au forma de mai jos:

procedura INIT (n, m, v, ig) este

┌ pentru i=1, m, 1 repeta

│ v(i) <- i

└

v₀ <- n-m-1

ig <- 1

sfarsit

procedura GEN (n, m, v, ig) este

i <- m

┌ cat_timp v_i = n-m+i repeta

│ i <- i-1

└

┌ daca i = 0 atunci

│ ig <- 0

│ altfel

│ v_i <- v_i+1

│ ┌ pentru j=i+1, m, 1 repeta

│ │ v_j <- v_j-1+1

│ └

└

sfarsit

Exemplu rezolvat. La masa rotunda a regelui Arthur sunt asezati n cavaleri. Fiecare cavaler este dusman cu vecinii lui. Merlin trebuie sa aleaga m cavaleri care sa o salveze pe printesa r_pita. Care sunt posibilitatile de alegere a echipei, astfel incit in echipa formata sa nu existe dusmani?

Fiecare cavaler este identificat printr-un numar intre 1 si n (pozitia lor la masa). Dusmanii unui cavaler se pot determina cu ajutorul unei functii:

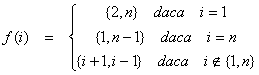
Algoritmul se bazeaza pe generarea tuturor multimilor de m elemente din multimea . Procedura de prelucrare este:

procedura PREL(v, n, m) este

gasit <- 0

i <- 1

┌ cat_timp (i£m) si (gasit=o) repeta

│ j <- i+1

│ ┌ cat_timp j£m si gasit=0 repeta

│ │ ┌ daca abs( v_i- v_j)=1 sau abs(v_i- v_j)=n-1 atunci

│ │ │ gasit <- 1

│ │ └

│ │ j <- j+1

│ └

│ i <- i+1

└

┌ pentru i=1, m, 1 repeta

│ scrie v_i

└

┌ daca v_i=n atunci

│ scrie 'Este solutie'

│ altfel

│ scrie 'Nu este solutie'

└

sfarsit

Programul principal in pseudocod va arata astfel:

scrie 'Introduceti numarul de cavaleri'

citeste n

scrie 'Introduceti dimensiunea grupului'

citeste m

executa INIT(n, m, v, ig)

┌ cat_timp ig¹0 repeta

│ executa PREL(v, n, m)

│ executa GEN(n, m, v, ig)

sfarsit

Pentru cazul particular, cind numarul de cavaleri este 6 iar dimensiunea grupului este 3 rezultatele vor fi afisate astfel:

Introduceti numarul de cavaleri: 6

Introduceti dimensiunea grupului: 3

Nu este solutie

Nu este solutie

Nu este solutie

Nu este solutie

Este solutie

Nu este solutie

Nu este solutie

Programul scris in Pascal se afla in Anexa A.L11.1 si C in Anexa B.L11.1.

2.1.b. Algoritmul recursiv.

Pentru generarea recursiva a elementelor vectorului v ce reprezinta se foloseste procedura:

procedura combr(p) este:

daca p=k+1 atunci

PREL();

altfel

daca p=1 atunci

pentru i=1,n,1 repeta

v[p]=i;

combr(p+1)

altfel

│ pentru i=v[p-1]+1,n,1 repeta

v[p]=i;

combr(p+1);

└

Programul scris in Pascal se afla in Anexa A.L11.2 si C in Anexa B.L11.2.

2. 2. Generarea combinarilor cu repetitie

Se numeste m-combinare cu repetitie a n elemente, un vector v cu elemente din multimea care are m elemente ce satisfac conditia:

v₁ £ v₂ £ £ v_m.

Daca inegalitatea dintre elementele vectorului este stricta se regaseste definitia combinarilor uzuale. Pentru generarea combinarilor cu repetitie se va folosi reprezentarea a) (printr-un vector v cu n componente).

2.2.a. Algoritmul iterativ.

Pentru generarea elementelor combinarilor cu repetitie in ordine lexicografica, metoda folosita presupune parcurgerea urma­torilor pas:

a) se initiaza elementele vectorului v la valoarea 1, adica v_i=1, pentru 1 £ i £ m;

b) pentru a se determina succesorul unui vector oarecare v=(v₁, v₂, v_m) se determina cel mai mare indice i pentru care v_i < n (daca un asemenea indice nu exista inseamna ca generarea s-a terminat ), iar succesorul vectorului, v', se obtine din v, inscriind pe pozitiile v_i, v_i+1, , v_m, valoarea v_i+1, adica v'=(v₁, v₂, , v_i+1, v_i+1, , v_i+1);

c) procesul de generare se incheie in momentul in care s-a ajuns la generarea vectorului v=(n, n, , n).

Procedurile de initializare si generare sunt:

procedura INIT(v, n, m, ig) este

┌ pentru i=1, m, 1 repeta

│ v_i <- 1

└

ig <- 1

sfarsit

procedura GEN(v, n, m, ig) este

i <- m

gasit <- 0

┌ cat_timp (i>0) si (gasit=0) repeta

│ ┌ daca v_i < n atunci

│ │ gasit <- 1

│ │ x <- v_i + 1

│ │ ┌ pentru j=i, m, 1 repeta

│ │ │ v_j <- x

│ │ └

│ │altfel

│ │ i <- i - 1

│ └

└

┌ daca gasit=0 atunci

│ ig <- 0

└

sfarsit

De exemplu, daca n=5 si m=3, elementele generate sunt: (1, 1, 1), (1, 1, 2), , (1, 1, 5), (1, 2, 2), , (1, 2, 5), , (5, 5, 5).

Daca se doreste folosirea unei variante cu santinela, aceasta trebuie asezata pe pozitia 0 a vectorului v si sa aiba valoarea diferita de n. In acest caz procedurile INIT si GEN au forma:

procedura INIT(n, m, v, ig) este

┌ pentru i=1, m, 1 repeta

│ v_i <- 1

└

v₀ <- n-1

ig <- 1

sfarsit

procedura GEN (n, m, v, ig) este

i <- m

┌ cat_timp v_i = n repeta

│ i <- i-1

└

┌ daca i=0 atunci

│ ig <- 0

│ altfel

│ x <- v_i + n

│ ┌ pentru j=i, m, 1 repeta

│ │ v_j <- x

│ └

└

sfarsit

Exemplu rezolvat. Sa consideram ca o cofetarie dispune de n tipuri de prajituri. Costul acestor prajituri este cost_i, cu 1 £ i £ n. Care sunt posibilitatile de cumparare a m prajituri astlel ca ele sa nu coste mai mult decit 'suma' lei?

O solutie a problemei se poate reprezenta sub forma unui vector v=(v₁, v₂, , v_m), unde v_i reprezinta tipul praji­turii i. Deoarece nu conteaza ordinea de cumparare a prajiturilor si prajiturile nu sunt neaparat distincte rezulta ca trebuie determinate toate solutiile de forma 1 £ v₁ £ v₂ £ £ v_m £ n

Deci trebuie generate toate combinarile cu repetitie cu m elemente din n. Pentru fiecare element generat se selecteaza acela pentru care pretul este mai mic sau egal decit 'suma'. Procedura de prelucrare este:

procedura PREL(v, n, m, suma, cost) este

s <- 0

┌ pentru i=1, n, 1 repeta

│ s <- s+cost[v_i]

└

┌ pentru i=1, n, 1 repeta

│ scrie v_i

└

┌ daca s £ suma atunci

│ scrie 'Este solutie'

│altfel

│ scrie 'Nu este solutie'

└

sfarsit

Programul principal in pseudocod va arata astfel:

scrie 'Introduceti numarul total de prajituri'

citeste n

scrie 'Introduceti costul prajiturilor'

┌ pentru i=1, n, 1 repeta

│ scrie 'Prajitura ', i, 'costa'

│ citeste cost_i

scrie 'Introduceti nunarul de prajituri de cumparat:'

citeste m

scrie 'Introduceti suma:'

citeste suma

executa INIT(n, m, v, ig)

┌ cat_timp ig¹0 repeta

│ executa PREL(v, n, m, suma, cost)

│ executa GEN(n, m, v, ig)

sfarsit

Pentru cazul particular, cind numarul total de prajituri existent este 4, costul prajiturilor este 5, 9, 8, respectiv 4 lei, numarul de prajituri de cumparat este 5 si se dispune de 30 lei rezultatele se vor asfisa astfel:

Introduceti numarul total de prajituri: 4

Introduceti costul prajiturilor

Prajitura 1 costa: 5

Prajitura 2 costa: 9

Prajitura 3 costa: 8

Prajitura 4 costa: 4

Introduceti nunarul de prajuturi de cumparat: 5

Introduceti suma: 30

1 1 1 1 1 Este solutie

1 1 1 1 2 Este solutie

1 1 1 1 3 Este solutie

1 1 1 1 4 Este solutie

1 1 1 2 2 Nu este solutie

Este solutie

2.2.b. Algoritmul recursiv.

procedura GEN_COMB_REP( i) este

pentru j=1,m,1 repeta

v[i]=j

daca i<n atunci

executa GEN_COMB_REP(i+1);

altfel

ok=1;

pentru k=1,n,1 repeta

daca v[k]>v[k+1] atunci ok=0;

daca ok=1 atunci

executa PREL()

sfarsit

3. Probleme propuse

1. Se considera un grup de n cadre didactice, din care se aleg comisii de examinare formate fiecare din m membrii. Pentru fie­care cadru se cunoaste gradul didactic (profesor, conferentiar, lector, asistent) si un cod de identificare. Sa se determine toate comisiile posibile in care cel putin un cadru este profesor (n si m, precum si codul si gradul fiecarei persoane se introduc de utilizator).

2. Se da un grup de n specialisti in comunicatii telefo­nice, din care se aleg echipe de interventii formate fiecare din m membrii. Pentru fiecare specialist se cunoaste calificarea (inginer, subinginer, tehnician, muncitor) si un cod de identifi­care. Sa se determine toate echipele posibile in care cel putin un specialist este inginer (n si m, precum si codul si gradul fiecarei persoane se introduc de utilizator).

3. Fie G un grup de n politisti, din care se aleg pa­trule formate fiecare din m membrii. Pentru fiecare se cunoaste gradul (locotenent, plutonier, sergent, soldat) si un cod de identificare. Sa se determine toate patrulele posibile in care cel putin un politist este locotenent (n si m, precum si codul si gradul fiecarei persoane se introduc de utilizator).

4. Se considera un grup de n ziaristi, din care se aleg echipe de reportaj formate fiecare din m membrii. Pentru fiecare ziarist se cunoaste specializarea (editorial, interviu, fotoreportaj, ancheta) si un cod de identificare. Sa se determine toate echipele posibile in care cel putin un ziarist este edito­rialist (n si m, precum si codul si gradul fiecarei persoane se introduc de utilizator).

5. Fie G un grup de n contabili, din care se aleg echipe de revizie formate fiecare din m membrii. Pentru fiecare contabil se cunoaste calificarea (universitate, institut, scoala medie, liceu) si un cod de identificare. Sa se determine toate echi­pele posibile in care cel putin un contabil are studii superioare (n si m, precum si codul si gradul fiecarei persoane se introduc de utilizator).

6 Se da un grup de n exploratori, din care se aleg echipe formate fiecare din m membrii. Pentru fiecare explorator se cunoaste specializarea (biologie, etnologie, ecologie, geolo­gie) si un cod de identificare. Sa se determine toate echipele posibile in care cel putin un explorator este ecolog (n si m, precum si codul si gradul fiecarei persoane se introduc de utilizator).

7 Se considera un grup de n sportivi, avind diferite inaltimi, unii dintre ei au inaltimi identice. Numarul n, precum si inalti­mea si un cod de identificare pentru fiecare se introduc de utilizator. Sa se listeze toate posibilitatile de a-i aseza intr- o coloana, unul in spatele altuia, in ordinea descrescatoare a inaltimii.

8 Fie G un grup de n boxeri, avind diferite greutati, unii dintre ei au greutati identice. Numarul n, precum si greutatea si un cod de identificare pentru fiecare se introduc de utilizator. Sa se listeze toate posibilitatile de a-i intro­duce in controlul antidoping, unul dupa altul, in ordinea descre­scatoare a greutati.

9 Se considera un grup de n copii, avind diferite virste, unii dintre ei au virste identice. Numarul n, precum si virsta si un cod de identificare pentru fiecare se introduc de utilizator. Sa se listeze toate posibilitatile de a-i introduce la vaccinare, unul dupa altul, in ordinea descrescatoare ( crescatoare ) a virstei.

10 Fie G un grup de n automobile, avind diferite capaci­tati, unele dintre ele au capacitati identice. Numarul n, precum si capacitatea si un cod de identificare pentru fiecare se introduc de utilizator. Sa se listeze toate posibilitatile de a le intro­duce la startul unui raliu, unul dupa altul, in ordinea crescatoare a capacitatii cilindrice.

11 Se da un grup de n camioane, avind diferite tonaje, unele dintre ele au tonaje identice. Numarul n, precum si tonajul si un cod de identificare pentru fiecare se introduc de utiliza­tor. Sa se listeze toate posibilitatile de a le introduce la o rampa de incarcare, unul dupa altul, in ordinea crescatoare a tonajului.

12. Se considera un tort pe care se pot pune bomboane. Bomboa­nele au n culori. Sa se afiseze toate posibilitatile de a aseza m bomboane identice sau diferite pe coliva, astfel incit sa fie cel putin o bomboana din fiecare fel (m si n se introduc de utiliza­tor astfel incat m>n).

13. Se da o matrice n x n cu elemente numere naturale, se cere sa se determine sumele de m valori de pe linii si coloane diferite care sunt mai mici decat o suma data.

Se considera o secventa de n numere naturale distincte.

a.Se cere sa se scrie un program de generare a m‑combinarilor cu repetitie a celor n numere.

b.sa se scrie un program de generare a m-combinarilor celor n numere.

15.Avind la dispozitie n (n>0) obiecte distincte si k cutii, sa se distribuie in prima cutie n₁ obiecte, in a doua n₂ obiecte, s.a.m.d. (n₁+n₂++n_k=n). Care sint posibilitatile de distribuire?

16. Cei m absolventi ai unei facultati trebuie sa urmeze niste cursuri de specializare. Se stie ca exista n directii de specializare. Sa se genereze toate posibilitatile de repartizare pe specializari ale absolventilor facultatii.

17. Aparatele de perforat plasate pe mijloacele de transport in comun folosesc 9 puncte de perforare situare in virfurile, mijloacele laturilor si centrul unui dreptunghi ABCD. Sa se genereze toate modalitatile in care poate fi perforat un bilet pentru toate combinatiile posibile ale punctelor de perforare, stiind ca biletul poate fi introdus in aparat cu latura AB in jos, pe oricare dintre cele doua fete.

18. Se considera o bara de lungime n si m repere de lungimi k(1),k(2),,k(m). Din bara trebuiesc taiate bucati de lungimea reperelor date astfel incit sa rezulte din fiecare reper cel putin o bucata, iar pierderile sa fie minime.

18. La admiterea in invatamintul superior este necesar sa se sustina n examene. Un candidat potential, ce stie ca poate reusi daca acumuleaza cel putin m puncte, isi determina posibilitatile de reusita. Care sint acestea?

19. Intr‑o intreprindere exista disponibile m cadre. Pentru realizarea unui anumit proiect, cele m cadre trebuie sa urmeze o perioada de specializare. Stiind ca pentru realizarea proiectului trebuie sa existe specialisti in n domenii, sa se genereze toate posibilitatile in care cadrele pot fi repartizate pe specializari, astfel incit proiectul sa se poata realiza dupa perioada de specializare( un cadru poate sa urmeze o singura specializare si toate cele m cadre trebuie specializate, m>=n ).

ANEXE

B.L11.1 COMB

La masa rotunda a regelui Arthur sunt asezati n cavaleri. Fiecare cavaler este dusman cu vecinii lui. Merlin trebuie sa aleaga m cavaleri care sa o salveze pe printesa r_pita. Care sunt posibilitatile de alegere a echipei, astfel incit in echipa formata sa nu existe dusmani? (varianta iterativa)

#include <stdio.h>

#include <conio.h>

int v[20],n,m,ig;

void INIT(int m, int n)

void PREL()

i++;

for(i=1;i<=m;i++)

printf('%d ',v[i]);

if(gasit) printf('Nu este solutien');

else printf('Este solutien');

getch();

void GEN()

void main()

B.L11.2 COMB REC

La masa rotunda a regelui Arthur sunt asezati n cavaleri. Fiecare cavaler este dusman cu vecinii lui. Merlin trebuie sa aleaga m cavaleri care sa o salveze pe printesa r_pita. Care sunt posibilitatile de alegere a echipei, astfel incit in echipa formata sa nu existe dusmani? (varianta recursiva)

#include <stdio.h>

#include <conio.h>

#define MAX 25

int n,v[MAX],k;

void PREL()

i++;

if(gasit)

printf(' Nu este solutien');

else

printf(' Este solutien');

getch();

void comb(int p)

else

for(i=v[p-1]+1;i<=n;i++)

void main()

B.L11. 7 Comb cu rep

#include<stdio.h>

#include <conio.h>

#define DIM 25

int m,n,v[DIM],ig;

int cost[DIM],suma;

void INIT()

void GEN()

void PREL()

void main()

printf('Introduceti numarul de prajituri de cumparat:');scanf('%d',&m);

printf('Introduceti suma:');scanf('%d',&suma);

INIT(n,m);

while(ig)

comb cu rep rec

#include <stdio.h>

# include <conio.h>

#define DIM 25

int ig,v[DIM],n,m;

int cost[DIM],suma;

void PREL()

void GEN(int i)

void main()

printf('Introduceti numarul de prajituri de cumparat:'); scanf('%d',&n);

printf('Introduceti suma:'); scanf('%d',&suma);

GEN(1);