Oscilatorul liniar armonic

Oscilatorul liniar armonic

Consideram o particula miscandu-se pe axa cu o energie potentiala: ,

unde e masa particulei iar pulsatia oscilatorilor in cazul clasic. Ecuatia Schrodinger atemporala devine:

Notam: si si ecuatia capata o forma mai simpla:

Studiem la inceput comportarea lui in regiunea asimptotica . In acet caz si ecuatia se reduce la:

care admite solutiile din care o pastram doar pe cea cu semnul minus pentru ca functia de unda sa ramana si la limitele .

Acum vom propune o solutie a ecuatiei Schrodinger de forma .

Introducand-0 in ecuatie, obtinem ecuatia Hermite :

Vom considera o serie de puterii:

Introducand seria de puteri in ecuatia Hermite obtinem:

sau

Ultima relatie este posibila daca in ambii membrii sunt egali coeficientii aceleiati puteri a lui , conditie care ne ofera relatia de recurenta a coeficientilor:

sau

Deoarece seria de puteri nu trebuie sa contina valori negative ale lui )deoarece cand seria ar deveni infinita si functia de unda nemarginita, exista un prim termen dat de

Cu solutiile si . Exista deci o serie cu puteri pare ale lui care incepe cu si una cu puteri ale lui care incepe cu .

Pentru ca functia de unda sa ramana marginita este necesar ca seria sa se transforme in polinom. Exista, deci un astfel incat si . Relatia de recurenta a coeficientilor devine:

Notand , aceasta expresie exprima cuantificarea energiei oscilatorului liniar armonic:

De aici extragem , energiile posibile ale oscilatorului. Observam ca nivelele de energie sunt echidistante : si ca nivelul fundamental

Exprima energia << de zero >> a oscilatorului : , a carui mitcare nu inceteaza niciodata. Functiile propri ale oscilatorului liniar armonic sunt:

unde este un fctor de normare a carui expresie rezulta din conditia de normare:

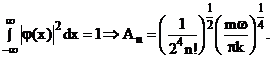
Polinoamele Hermite: unde sau si satisfac relatia de

recurenta cu expresia generala:

Astfel avem: , s.a.m.d.

Einstein a explicat anularea caldurii sferice a solidelor cand temperatura tinde la zero absolut imaginand solidul ca un ansamblu de oscilatori armonici, iar Max Planck a dedus expresia densitatii spectrale de energie a radiatiei corpului negru echivaland atomii peretilor cu care interactiona radiatia electromgnetica, de asemenea cu miscarea oscilatorie armonica.