Elemente ale teoriei complexitatii corelate cu teoria informatiei

Elemente ale teoriei complexitatii corelate

cu teoria informatiei

Studii preliminare ale teoriei complexitatii

In timp ce studile preliminare privind caracteristicile de baza ale complexitati apartin domenilor ingineriei electrice (inclusive calculatoarelor) si matematicii , respectiv fizicii , primele asemene studii au fost realizate in domeniile biologiei , ingineriei electrice, fizicii , in stransa legatura cu matematica , chimia etc. Importanta acestui domeniu a impus studii internationale sistematice, inclusiv infiintarea unor institute de cercetari dedicate studiului caracteristicilor de complexitate precum cel de la Santa-Fe (California). Dintre cele mai importante studii asupara complexitatii apartinand unor domenii stiintifice diferite, publicate in ultimi ani, vom mentiona lucrarile din domenile: fizicii , chimiei , biologiei , interdisciplinar ingineriei electrica-biologie , stiintelor economice stiintelor sociale , teoriei cunoasteri etc. .

Primele lucrari importante ale Teoriei complexitatii in fizica sunt cele ale lui P.W. Anderson, care a explicat comportarea macroscopica a sistemelor complexe [indeosebi din domeniile supraconductoarelor, fluiditatii, candensari nucleonilor in nuclee, stelelor neutronice . materialelor nitroase ( sticloase ) ] prin aparitia unor discontinuitati ( samburi, precum vartejurile din curgerile turbulente, mutatiile genetice etc. ) drept consecinta a unei rupture spontane de simetrie ( Spontaneous Symmetry Breaking ). Cresterea auto catalitica stocastica a acestor "samburi" este corelata cu alte caracteristici importante ale sistemelor complexe, precum scalarile lor fractale , legile putere etc., iar unele caracteristici ale complexitati privind autoorganizarea in sisteme aflate in stari de ne echilibru, comportarile haotice si tranzitia la starile ordonate etc. au fost studiate de I. Prigogine.

Descrierea cantitativa detaliata a proceselor fizice complexe a fost realizata de catre K.G.Wilson ,prin metoda sa a "grupului de renormare",constand in integrarea succesiva a fluctuatiilor ,pornind de la fluctuatiile la scara atomica si continuand pentru niveluri mai inalte de organizare a materiei ,pana la medierea fluctuatiilor pentru toate nivelurile de organizare a materiei.Reiese ca -in prezent -cea mai buna definitie a complexitatii se realizeaza prin referire la starile si procesele in care sunt concomitent active fluctuatii semnificative la diferite niveluri de organizare ale materiei.

Deoarece identificarea procedurilor de 'renormare'prezinta -pentru multe sisteme complexe-dificultati considerabile,P.G.de Gennes (laureate al Premiului Nobel pentru Fizica in 1991 )a aratat ca 'metodele simple elaborate pentru studiul fenomenelor de ordine in sistemele pot fi generalizate pentru forme mai complexe ale materie,in particular pentru cristalele lichide si polimeri'.

Reiese ca unele notiuni, organizate in secvente universale (spre exemplu :discontinuitate microscopica ≡ 'sambure' →crestere/acomodare →autocataliticitate→legi de tip putere →fractali etc.) ,permit descrierea proprietatilor sistemelor complexe de nature foarte diferite.Aceasta constatari evidentieazaexistenta unor caracteristici de universalitate,care guverneaza structurile si evolutiile sistemelor complexe de naturi arbitrare.

Trebuie sa subliniem ca de asemenea -spre deosebire de caracteristicile de universalitate -printre parametrii care descriu sistemele complexe ,exista si uniiparametri (adimensionali) independenti de marimea sistemului ,dar dependenti de natura acestuia -asa numitele criterii de (numere) de similitudine.

Avand in vedere aplicatiile importante in inginerie ale fizicii materialelor ,consideram util sa evidentiem in continuare o serie de caracteristici specifice de complexitate observate in studiul :

(i)         fluidelor in curgere (hidraulica),

(ii)       materialelor elastice (folosite in ingineria mecanica si in constructii, inclusiv pentru studii si proiectari anti-seismice),

(iii)     materiale dielectrice si respectiv magnetice (in domeniul energiei elastice indeosebi).

Elemente de teoria informatiei

Definirea si expresia gradului de nedeterminare corespunzand unui colectiv static . Folosind relatia lui Boltzmann,specialistul american Claude Shannon si colab .sai au elaborate teoria generala a informatiei .S-a pornit de la notiunea de grad de nedeterminare [simbol H ()] asociat unui colectiv statistic complet de evenimente incompatibile C≡,caracterizate prin probabilitati pi de aparitie a diferitelor evenimente Ei i(1,2, . .,n).

Deoarece studiile specialistilor americani au fost continuate si de catre matematicienii rusi (indeosebi Hincin si Kolmogorov ),prezentam in cele ce urmeaza definirea gradului de nedeterminare pornind de la proprietatile functiei

H(), in baza axiomatizarii date de Hincin:

simetrie H ()] =H (),

valoarea maxima pentru distributia uniforma :

H ()= maxim pentru ,

3)proprietatea de "prelungire": H ()=H () adica adaugarea unui element imposibil (de probabilitate nula )nu modifica valoarea functiei gradului de nedeterminare,

4)continuitate: functia H () trebuie sa fie continua in raport cu toate variabilele sale : ,

5)liniaritate : , unde si sunt gradele de nedeterminare corespund multimii-produs cartezian al coletivelor statistice C si C', respective colectivului statistic C',in conditiile in care s-a produs (a aparut ) evenimentul Ei.

Pornind de la definitia precedenta a gradului de nedeterminare ,reiese ca -pentru collective discrete de evenimente -functia H (),este data de expresia:

,

in care :a si b sunt constante satisfacute conditiile : a>0 si b>1

Pentru colective statistice continue (descries de densitatea de probabilitatea ),functia gradului de nedeterminare este :

unde Δx este o "cuanta"(convenabil aleasa) a variabilei x .

Deoarece -dupa efectuarea unor determinari experimentale-se gaseste:

(i)         interval de incredere asociat valorii "adevarate" (estimate aici prin valoarea medie ):

,

dar: (ii)nu este posibil sa se gaseasca pozitia valorii "adevarate" ("sperantei matematice ")in interiorul intervalului de incredere ,singura presupunere posibila fiind o distributie uniforma in acest interval de incredere:

pentru , pentru

Reiese urmatoarea expresie a grdului de nedeterminare asociat distributiei uniforme a valorii "adevarate"in interiorul intervalului de incredere :

Entropia informationala (cantitatea de informatie)

Omparand expresiile (50) si (11), se constata ca functia gradului de nedeterminare H() reprezinta valoarea medie (teoretica) a asa numitei entropii informationale, definite prin relatia:

Deoarece pi>1,b>1 si a >0,entropia informationala este o cantitate pozitiva .Se constata de asemenea ca-daca pi scade spre 0 ,entropia informationala creste lent spre infinit ,fapt care poate fi interpretat drept "cantitate considerabila (mare) de informatii capatata la aparitia unui eveniment de posibilitate redusa (mica)".Aceasta constatare explica cumva denumirea de cantitate de informatie folosita de asemenea pentru entropia informationala.

De regula ,unitatile entropiei informationale sunt definite pentru a =1:bit (denumire formata din literele subliniate in denumirea Engleza "binary information unit ), pentru b =2,nit (idem pornind de la denumirea natural information unit), pentru b=e≈2,718281 . ..(nr lui Euler), si respectiv dit (decimal information unit) pe b =10.

Pentru o distributie continua ,entropia informationala va fi data de expresia :

S=−a logb γ +constant.

Se constata cu usurinta ca expresia Bolzmann (48) a entropiei termodinamice constituie un caz particular al relatiei (57), corespunzand alegerii :a=kB, b=e,variabilele continue distribuite corespunzator in acest caz celor ale spatiului fazelor.

Cantitatea de informtie aparenta obtinuta prin cea de a n a determinare dintr un set de masurari este definite ca fiind egala cu diferenta valorilor functiei de nedeterminare dupa cea de a (n−1) a determinare si respective dupa cea de a n a determinare fata de multimea rezultatelor obtinute in primele (n−1) determinari, cu ajutorul expresiei :

,

prin abaterile patratice medii dupa primele (n−1) respective n determinari .

Desigur ,valorile cantitatii aparente de informatie sunt de regula positive ,iar:

a)aparitia unor valori negative ale cantitatii aparente de informatie poate indica:

(i) o eroare grosolana ,intervenind in ultima determinare (a n a ),

(ii) o "aglomerare"excesiva intamplatoare a primelor (n−1) determinari ,corectata cumva de rezultatul celei de a n a determinare;

b)valorile repetate foarte mici ale cantitatii aparente de informatie pot indica faptul ca masurarile si au atins deja acopul lor cognitive ,si ca prelungirea in continuare a procesului de masurare nu este eficienta (nici din punct de vedere cognitive si nici din punct de vedere economic).

Elemente de baza privind teoria testelor statistice.

Procedura de testare a unei ipoteze statitice H este bine-cunoscuta. Pentru un spatiu dat de parametri de univocitate, se definesc un vector de parametric de test si doua zone: de acceptare , respectiv complementara sa . Probabilitatea ca respingand ipoteza statistica H, ea sa fie totusi adevarata, da criteriul de acceptare/respingere a ipotezei statistice studiate: dupa cum riscul de eroare q<0,001( 0.1%), respective q>0 ( 2%), ipoteza statistica este respinsa, respective este acceptata. Testele statistice clasice (Pearson), Kolmogorov, Massey, Sarkady, etc. destinate studiului compatibilitatii anumitor distributii teoretice cu rezultatele experimentale sunt folosite uneori de asemenea pentru evaluarea compatibilitatii globale a unor relatii teoretice si a unor simulari numerice fata de rezultatele experimentale existente.

Consideram util sa subliniem faptul ca - spre deosebire de situatia de la sfarsitul secolului XIX- lea [cand lordul Kelvin afirma "cerul fizicii este senin, exceptand doi mici "nori" corespunzand "catastrofei ultraviolete" si -respectiv radiatilor X (Rontgen) ], la inceputul secolului nostrum (al XXI-lea ) cerul fizicii este intunecat; spre exemplu, dintre cele sase etape (considerate foarte probabil in prezent) ale evolutiei Universului doar domeniul de timp centrat pe (re)combinare electronilor di protonilor cu formarea de atomi de hydrogen este bine inteles si descries cu precizie de legile fizicii actuale in timp ce etapele corespunzand: (i) interactiunilor unificate, (ii) "inflatiei" Universului, (iii) incalzirii Universului, (iv) inceperii procesului denumit acum "Big Bang", (v) inceperii expansiunii accelerate a Universului, nu pot fi descries (cantitativ, si nici macar calitativ) de modelele teoretice actuale ale fizicii.

De fapt, dupa succesele sale exceptionale obtinute (pana in aproximativ 1965) in descrierile sistemelor simple si - respective complicate (in principal cu ajutorul fizicii cuantice, fizicii nucleare si - respective - teoriilor relativitatii, prin elaborarea reactoarelor de fifiune nucleara, a dispozitivelor semiconductoare si - respective- laser etc. ), fizica a suferit o adevarata "ciocnire frontala" cu problematica sistemelor complexe. Din pacate, fizica si - in general - stiintele naturii nu au fost pregatite pentru descrierea sistemelor complexe , instrumentele lor matematice destinate acestui scop [teoria multimilor "vagi" (fuzzy sets ) teoria ecuatilor diferentiale nelimitate si teoria haosului, teoria ecuatilor diferentiale deordin intregsi teoria fractalilor etc.] fiind insuficiente pentru " provocarea descrierii sistemelor fizice complexe " .

Din acest motiv, studiul complexitatii pare sa fie cel mai important obiectiv al fizicii in acest secol, atingerea sa depinzand insa si de completarea (inclusive perfectionarea) instrumentelor matematice ale fizicii.

Aparitia teoriilor complexitatii si informatiei

Se pare ca prima lucrare moderna care a evidentiat unele caracterstici esentiale ale complexitati ( stransa sa legatura cu statica matematica , universalitatea care ii este asociata etc.) a fost cea a lui Ettore Majorana.

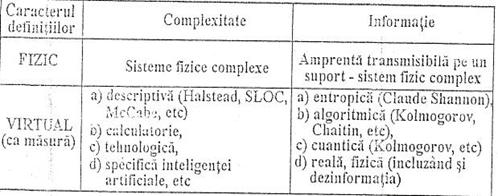
Teoriile matematice moderne ale complexitati si respectiv informatiei au aparut impreuna in cadrul studiilor comunicatiilor electrice efectuate de Claude Shannon si Warren Weaver. Tabelul 3 prezinta o sinteza a principalelor tipuri de definitii ale complexitatii si respectiv informatiei.

Drept exemplu de sisteme fizice complexe si informatie asociata ( transmisa ), figura 3 prezinta: a) lantul polipeptidic al acidului de zoxiribonucleic ( ADN ) - support al informatiei transmisa prin intermediul genelor, b) structura acidului dezoxiribonucleic, c) structurile bazelor azotate- componente ale informatiei denetice, d) structura unei gene-purtator ( caraus ) al informatiei genetice .

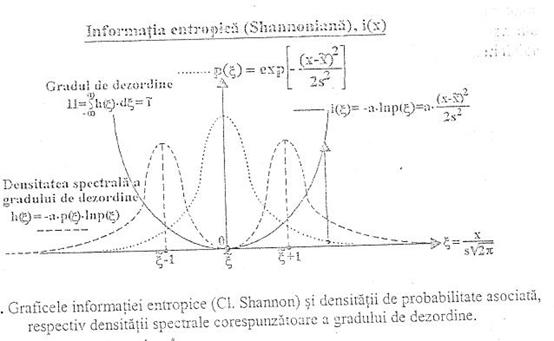
Ca exemplu particular privind definirea informatiei entropice (CI Shannon ), figura 4 prezinta graficele: (i) densitatii probabilitatii distributiei normale unidimensionale ( Gauss ), (ii) informatiei entropice ( Shannon ) corespunzatoare (iii) densitatii spectrale a gradului de dezordine. Pentru a simplifica descrierile cantitative si graficele corespunzatoare au fost folosite in locul valorilor individuale x ale parametrului fizic considerat valorile lor reduse definite prin relatia:

,

unde s este abaterea ( eroarea ) patratica medie a distributiei normale 1D ( Gauss ) a parametrului x. Se constata ca informaia entropica ( Shannon ) :

i(x)= -a*ln p(x) ,

este mai mare pentru valorile individuale cu mica probabilitate de aparitie, deoarece constatarea existentei lor prezinta o informatie mai inalta decat cea a constatari existentei celor mai probabile valorii individuale

Aplicatii ale cantitatii reale de informatie

Evaluarea cantitati de informatie fizica aparenta pornind de la expresia Shannon - Khinckin a gradului de dezordine ( nedeterminare ) asociat unui colectiv statistic de eveniment :

,

unde : a > 0 si b>1 putem determina gradul de nedeterminare asociat unui colectiv statistic continuu ( descries de densitate de probabilitate p(x)) drept :   

,

unde ∆(x) este "cuanta" variabile x.

Reiese expresia gradului de dezordine corespunzand distributiei statistice uniforme associate intevalului de incredere al valorii adevarate:

Se constata ca atat gradul de nedeterminare asociat distributiei normale unidimensionale a valorilor individuale cat sic el asociat distributiei uniforme din intervalul de incredere care corespunde valorii adevarate, include factorul logaritmic al abaterii patratice medii corespunzand valorii individuale, respecti valorii adevarate.

Cantitatea de informatie aparenta obtinuta prin cea de a n a determinare a ansamblului de masurari este definite ca diferenta a gradelor de nedeterminare ramase dupa cea de a ( n-1 ) a si respective dupa cea a n a determinare.

Avand in vedere faptul ca 4 si 7 ale gradelor de dezordine care corespund valorilor individuale si respectin valorilor adevarate ale parametrilor fizici studiati reiese ca informatia aparenta obtinuta prin cea de a n a determinare poate fi exprimata in functie de abaterile ( erorile ) patratice medii corespunzand ansamblului rezultatelor experimental obtinute pana la cea de a (n-1) a determinari si pana la cea de a n a determinare inclusiv , prin expresiile :

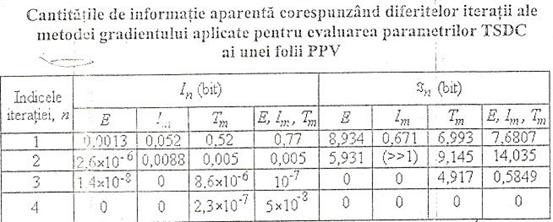
Pentru a evalua viteza de convergenta a unor proceduri de aprozimatii succesive vom folosi deasemenea expresia:

,

unde este limita erori ptratice medii dupa un numar foarte mare de iteratii convergente. Tabelul 4 reprezinta valorile celor doua tipuri de informatii aparenta carecorespund metodei gradientului aplicate crentilor de poralizare stimulate termic (TSDC) pentru : a) variatii exclusive ale : (i) energiei de activare E , (ii) intensitatii mazime Im a curentului TSDC , (iii) temperaturi Tm ,sau pt : b) variatii concomitentale acestor 3 parametri (E,):

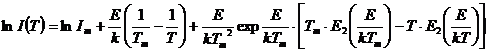
pentru o folie de poli (p- fenilen - vinilen ) PPV .

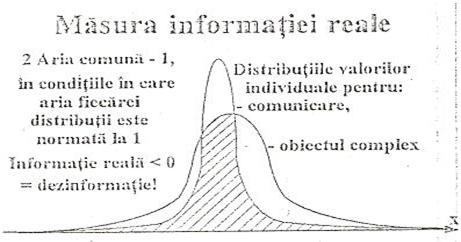
Evaluarea cantitatii de informatie adevarate

Dupa cum este bine cunoscut descrierea sistemelor complexe este strans legata de anumite distributii de proabiliatati, cea mai simpla asemena distributie fiind distributia normale uni dimensionala ( Gauss ) .in cea ce priveste comunicarile referitoare la acest obiect complex ele sunt date de o alta distributie 1 D , care difera intrucatva de cea adevarata. Dupa cum reiese din examinare figurii exista desigur o zona de suprapunere a acestor distributii, a corar marime creste pt reproduceri mai exacte ale obiectului studiat. In conditiile in care ambele aceste distributii unidimensionale sunt normate la 1 este posibil sa se defineasca masura cantitati de informatie adevarata (fizica ) cu ajutorul expresiei:

de sup rapunere -1.

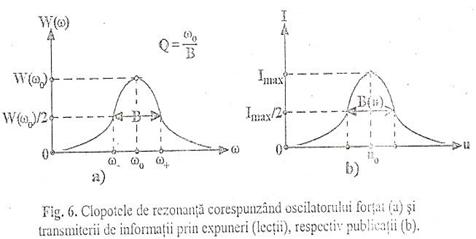
Modelul rezonant al cantitatii de informatie transmise prin expuneri (lectii) sau publicatii. O alta tema majora din acest domeniu se refera la eficienta transmiteriii informatiilor reale.

Vom considera aici ca transmiterea informatiilor prin expuneri sau publicatii este un proces oarecum resonant, asemanator oscilatiilor fortate. Este bine-cunoscut faptul ca dependenta de frecventa a excitatiei periodice externe, a energiei transmise unui oscillator de frecventa prorprie este descrisa de expresia:

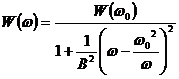
Pentru frecventele pentru care energia transmisa se reduce la jumatate din cea maxima , avem:

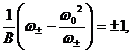deci:

Rezulta ca semnificatia fizica a parametrului B este cea de "semilargime" a clopotului de rezonanta. Dupa cum este cunoscut, intre latimea benzii de trecere si factorul de merit Q pentru selectivitatea rezonantei exista relatia:

.

Deoarece cantitatea si chiar calitatea informatiei transmise depinde de parametrii receptorului, vom presupune existenta unei dependente asemanatoare a cantitatii de informatie transmise prin expuneri sau publicatii de parametrii receptorului, notatii prin u.

Consideram ca acest model theoretic este important in multe domenii, precum acela privind evaluarea:

(i)         eficienta proceselor de predare,

(ii)       calitatii activitatilor stiintifice.

Complexitatea si aplicatiile sale tehnice

In ciuda largii diseminari a multor rezultate ale teoriei complexitatii, exista inca unii specialisti care exprima dubii privind eficienta practica a acestei noi teorii stiintifice. Pentru a clarifica acest aspect deosebit de important, vom mentiona doar:

a)          aplicatiile propagarii undelor solitare prin fibre optice pentru transmisiile de informatii de inalta performanta;

b)          sinteza rezultatelor, evidentiind prezenta si aplicatiile anumitor caracteristici de complexitate in multiple procese;

c)          spre deosebire de industria informatiei, nu se poate vorbi despre o industrie a complexitatii, dar . aproape in intreaga industrie moderna este o industrie a sistemelor complexe.

O alta dovada clara a obiectivitaii teoriei complexitatii si emergentei sale idirectii total diferite o constituie studiile asupra posibilitatilor de descriere a curgerilor in regim turbulent.

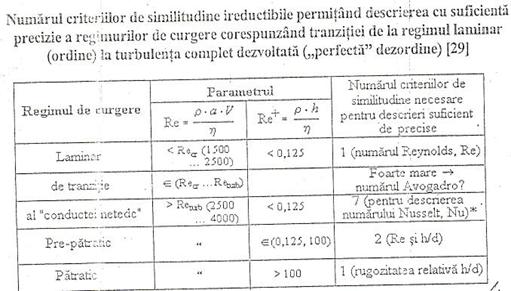
Or, in lucrarile au fost realizate:

(i)         compresia informatiilor prin utilizarea criteriilor se similitudine,

(ii)       eliminarea oricaror redundante,

(iii)     evidentierea continutului de informatie algoritmica.

In plus, tabelul de mai sus indica faptul ca aceste lucrari au evidentiat faptul ca numarul criteriilor de similitudine ireductibile satisface cerintele (i)-(iii) pentru gradul de complexitate efectiva, inclusive privind esitenta unui:

(i)         maxim "ascutit" intre starile de ordine si cele de "perfecta" dezordine (turbulenta complet dezvoltata haos generalizat).

Concluzii

Consideram ca - inclusive in abordarea matematica a transmiterii informatiei - trebuie acordata o mare atentie calitatii intriseci a informatiei transmise, deoarece scopul nu este de a transmite informatii oarecare, ci acela de a transmite informatii de gradul dorit de exactitate "fizica".