Oscilatii si unde - Micarea oscilatorie armonica ideala

Oscilatii si unde

1. Notiuni generale

Se numeste oscilatie fenomenul fizic in decursul caruia o anumita marime fizica a procesului prezinta o variatie periodica sau pseudo-periodica. Un sistem fizic izolat, care este pus in oscilatie printr- un impuls, efectueaza oscilatii libere sau proprii, cu o frecventa numita frecventa proprie a sistemului oscilant. Oscilatiile pot fi clasificate in functie de mai multe criterii.

Din punct de vedere al formei de energie dezvoltata in timpul oscilatiei, putem intalni: (i) oscilatii elastice, mecanice (au loc prin transformarea reciproca a energiei cinetice in energie potentiala); (ii) oscilatii electromagnetice (au loc prin transformarea reciproca a energiei electrice in energie magnetica);

(iii) oscilatii electromecanice (au loc prin transformarea reciproca a energiei mecanice in energie electromagnetica).

Din punct de vedere al conservarii energiei sistemului oscilant, putem clasifica oscilatiile in: (i) oscilatii nedisipative, ideale sau neamortizate (energia totala se conserva); (ii) oscilatii disipative sau amortizate (energia se consuma in timp) (iii) oscilatii fortate sau intretinute (se furnizeaza energie din afara sistemului, pentru compensarea pierderilor).

Marimi caracteristice oscilatiilor periodice

Sa notam cu S(t) marimea fizica ce caracterizeaza o oscilatie. Atunci, daca T este perioada oscilatiei, marimea S are aceai valoare la momentul t si la un moment ulterior, t + T:

S(t) = S(t+T )

Oscilatiile armonice reprezinta acel tip de oscilatii in care marimile caracteristice se pot exprima prin functii trigonometrice (sinus, cosinus ) sau prin functii exponentiale de argument complex. Acele oscilatii care nu sunt armonice, se pot descompune in serii Fourier de functii. Reamintim, de asemenea, formulele lui Euler, care vor fi utile in calculele urmatoare:

Miscarea oscilatorie armonica apare foarte des in situatiile practice. Un exemplu foarte la indemana il constituie bataile inimii. Se spune ca Galilei folosea bataile inimii sale pentru a cronometra miscarile pe care le studia.

2 Micarea oscilatorie armonica ideala

In absenta unor forte de frecare sau de disipare a energiei, miscarea oscilatorie este o miscare ideala, deoarece energia totala a oscilatorului ramane constanta in timp. Micarea este reversibila, astfel ca dupa o perioada oscilatorul revine in pozitia initiala si procesul se reia. Forta care determina revenirea oscilatorului in pozitia initiala si care permite continuarea oscilatiei se numete forta de revenire. Aceasta forta de revenire poate fi forta elastica dint-o lama metalica, presiunea dintr-un tub si, in general, orice forta care produce o deformare elastica.

Sa consideram un oscilator mecanic format dintr-un resort elastic si un corp punctiform, de masa m, legat la capatul liber al resortului, ca in fig.1.a. Daca se pune corpul in miscare prin intermediul unei forte si daca nu exista frecari, sistemul va efectua o micare periodica in jurul pozitiei de echilibru, numita oscilatie ideala.

Forta elastica din resort, _e^F , este singura forta din sistemul mecanic, aa ca putem scrie formula fudamentala a dinamicii sub forma:

ma = - k y

unde k este constanta elastica a resortului, iar y este alungirea acestuia (y se numete elongatia miscarii) .

Ecuatia de micare a corpului devine:

m a + k y = 0

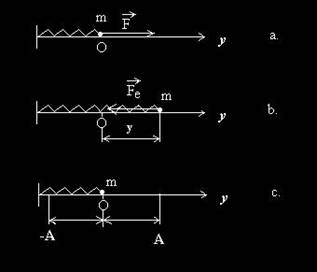
Fig. 1. Oscilator mecanic ideal a) momentul initial b) alungirea y produce forta de revenire _eF

c) amplitudinea micarii oscilatorii.

Acceleratia corpului reprezinta derivata de ordinul doi la timp a vectorului deplasare, de aceea ecuatia de micare devine:

Reprezentarea marimilor vectoriale periodice se poate realiza si prin intermediul fazorilor. Fazorul este un vector rotitor in sens trigonometric pozitiv intr-un plan Oxy, care are vitexa unghiulara

₀ . Lungimea fazorului este egala cu modulul vectorului pe care il reprezinta, adica fazorul este egal cu amplitudimea micarii oscilatorii. Faza vectorului reprezentat este egala cu unghiul format de fazor cu axa orizontala, Ox. Vectorul reprezentat este egal cu proiectia fazorului pe axa verticala Oy. Fazorul din fig. 2 reprezinta elongatia oscilatorului ideal, in diferite momente de timp.

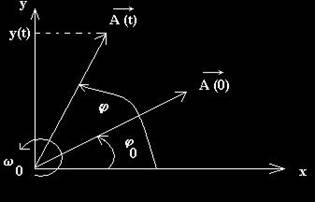
Fig. 2. Reprezentarea fazoriala a oscilatiei

Marimile fizice caracteristice ale oscilatorului ideal pot fi reprezentate grafic in functie de timp. Daca faza initiala este nula, se obtin graficele functiilor y = f(t , v = f(t) si a = f(t) din fig.

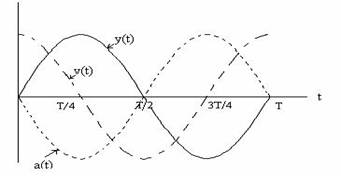
Fig. Elongatia, viteza si acceleratia oscilatorului ideal in functie de timp

Energia  mecanica a oscilatorului ideal este constanta, ceea ce constitue legea conservarii energiei mecanice a oscilatorului ideal.

In decursul oscilatiei ideale, energiile cinetica si potentiala elastica ale oscilatorului ideal sunt variabile in timp, transformandu-se una in alta, in aa fel incat suma lor sa ramana constanta. In fig.4 sunt reprezentate energiile cinetica, potentiala si totala in functie de elongatia y. Se poate observa ca desi energia potentiala este variabila, fiind reprezentata de parabola din figura, totusi energia mecanica a oscilatorului ideal este constanta.

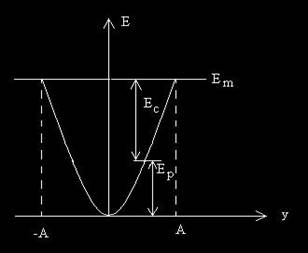
Fig.4. Energiile cinetica, potentiala si totala in functie de elongatia oscilatorului ideal.

Conservarea energiei mecanice a oscilatorului constituie efectul direct al faptului ca fortele elastice sunt forte conservative. Caracterul oscilant al miscarii se poate constata si din transformarea periodica a energiei cinetice in energie potentiala si reciproc.