 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
ECHILIBRE CHIMICE IN SISTEME ETEROGENE ECHILIBRE DE PRECIPITARE
![]()
In acest capitol:
Consideratii teoretice
Intrebari
Probleme propuse
Probleme rezolvate
![]()
Consideratii teoretice
Echilibre in sisteme eterogene
In practica analitica adeseori avem de-a face cu sisteme complexe, de exemplu, cand separam precipitate sau cand aducem in solutie o substanta solida. In asemenea cazuri se lucreaza cu sisteme eterogene, caracterizate prin existenta in interior a unor suprafete de separare ce delimiteaza partile componente omogene ale sistemului, numite faze. In marea majoritate a acestor sisteme eterogene, una din faze este o solutie apoasa, iar a doua faza este formata fie dintr-un compus solid insolubil in apa, fie dintr-un compus lichid nemiscibil cu apa.
Astfel, in sistemul eterogen format dintr-un precipitat in echilibru cu solutia saturata, precipitatul constituie faza solida, iar solutia saturata, faza lichida. O faza se defineste ca fiind o parte omogena a unui sistem, separata de celelalte parti ale acestuia prin suprafete fizice, la nivelul carora apare o variatie brusca a proprietatilor. Echilibrele chimice care se produc in mai multe faze se numesc echilibre eterogene.
Echilibrele chimice eterogene se pot grupa in functie de natura fazelor, dupa cum urmeaza :
echilibre chimice eterogene, care se produc intre o faza solida si o faza lichida ;
echilibre chimice eterogene, care se produc intre o faza lichida si o faza gazoasa ;
echilibre chimice eterogene, care se produc intre o faza apoasa si un al
doilea solvent nemiscibil cu apa.
In caracterizarea echilibrelor eterogene trebuie avut in vedere, faptul ca echilibrele chimice se produc atat in fiecare faza care alcatuieste sistemul considerat, cat si la suprafata de separare a acestora.
Echilibrele eterogene si indeosebi cele care se produc intre doua faze ofera posibilitatea separarii compusilor chimice in cursul analizei chimice.
Echilibre de precipitare. Compusi greu solubili
Reactiile analitice bazate pe procese de precipitare constituie unul dintre capitolele de baza ale chimiei analitice, deoarece un numar mare de separari, identificari si determinari, frecvent intalnite in analiza chimica, se bazeaza pe formarea sau dizolvarea precipitatelor.
Pentru intelegerea conditiilor de echilibru care exista in solutiile ce conduc la formarea de precipitate, cat si pentru explicarea factorilor care favorizeaza dizolvarea precipitatelor, trebuie sa se tina seama ca aceste sisteme sunt constituite dintr-o faza solida si o faza lichida (solutie si precipitat). Echilibrul fazei solide cu solutia, se atinge numai la starea de saturare.
Marea majoritate a sarurilor greu solubile se comporta in solutie ca un electrolit tare, adica la dizolvarea in apa nu se gasesc moleculele lor ci ionii liberi corespunzatori.
Dat fiind ca nu se cunoaste nici o substanta absolut insolubila, reactiile cu formare de precipitate nu sunt reactii totale, ducand la stabilirea unui echilibru intre faza solida si faza lichida, denumit echilibru de precipitare (echilibru de solubilitate).
Cunoasterea legilor care guverneaza acest echilibru are o deosebita importanta in chimia analitica, reactiile cu formare de precipitate si cele de dizolvare avand un rol deosebit in reactiile de identificare si de separare. Este bine cunoscut faptul ca diferitele substante se dizolva in apa in proportii diferite, insa ori de cate ori se prepara o solutie saturata dintr-o anumita substanta, solutia rezultata are aceeasi concentratie. Aceasta concentratie, exprimata in mol/l, notata cu S, reprezinta solubilitatea molara a substantei respective.
Solubilitatea molara reprezinta numarul de moli dizolvati ai unei substante aflate intr-un litru de solutie saturata.
Solubilitatea unei substante intr-un dizolvant la temperatura constanta este constanta.
Compusii greu solubili nu constituie, din punct de vedere analitic, o clasa anume de compusi chimici, ei putand fi considerati ca un caz particular al complecsilor. Formarea lor poate fi considerata ca rezultatul unui echilibru de tip donor - acceptor, in care particula caracteristica este un ion, iar donorul un compus greu solubil.
Daca in echilibrul de complexare, concentratia complexului format este sub limita de solubilitate a acestuia, se poate scrie :
A + X D (1)
in care:
A este acceptorul particulei X (ion), cu care formeaza complexul D.
Echilibrul este caracterizat de constanta de instabilitate :
K′ (Ki) = ![]() (2)
(2)
Concentratia complexului D in solutie, in forma neionizata, nu poate depasi o anumita valoare , care defineste solubilitatea limita a acestuia in solventul dat. Cand valoarea concentratia complexului D atinge valoarea , solutia devine saturata in acest compus. Daca concentratiile speciilor A si X introduse in sistem conduc la formarea complexului D in concentratie mai mare decat valoarea solubilitatii limite , excesul de complex precipita, trecand astfel in faza solida.
Pentru un astfel de sistem, se poate scrie echilibrul eterogen :
D(solid) D(solutie) A + X (3)
pentru care se poate scrie :
[A] · [X] = K · [D] = K · s = constant (4)
Pe baza relatiei 4, se poate observa ca, pentru solutia saturata a complexului D, produsul concentratiilor ionilor acestui compus este constant. Aceasta constanta este denumita produs de solubilitate si se noteaza cu Ps ( sau Ks) :
Ps = [A] · [X]
Produsul de solubilitate permite sa se determine cantitatea limita de substanta dizolvata, deci solubilitatea unui compus, si totodata sa se prevada conditiile in care se poate forma faza solida (precipitatul), pe baza echilibrului de precipitare.
Adaugand solutiei ce contine specia A solutia care contine specia X, faza solida nu apare atat timp cat, [D] < , ceea ce permite sa se deduca, pe baza relatiei 4 ca precipitarea nu are loc daca :
[A] · [X] < Ps
Precipitarea poate avea loc deci, numai daca in sistem se introduc speciile care formeaza compusul greu solubil, in concentratii totale al caror produs
depaseste valoarea Ps.
Echilibrul fazei solide cu solutia se atinge numai la starea de saturare. Acest proces dinamic dintre faza solida a unei sari de tip MA si ionii din solutia saturata se exprima :
MA MA M+ + A− Ps = [M+] · [A−] (7)
faza solida solutie saturata
Reversibilitatea acestei reactii se poate dovedi experimental, deoarece la echilibru cantitatea de substanta solida care se dizolva este egala cu cantitatea de substanta solida care se formeaza prin reactia ionilor M+ si A−, ceea ce arata ca viteza de dizolvare este egala cu viteza de precipitare.
Produsul de solubilitate Ps este o constanta si se defineste ca produsul concentratiilor tuturor ionilor unei sari dintr-o solutie saturata, la o temperatura data.
Pentru calcule mai riguroase, in locul concentratiilor este necesara introducerea activitatilor.
Din motive simplificatoare, intelegerea si stabilirea conditiilor de formare sau de dizolvare a precipitatelor se studiaza, de obicei, numai pe baza relatiei simple, fara a tine seama de taria ionica.
Totusi, deoarece solutiile care fac obiectul analizei chimice sunt amestecuri de diferite saruri, neglijarea tariei ionice in calculele de solubilitate si ale produsului de solubilitate nu este totdeauna posibila, mai ales atunci cand este vorba si de saruri cu o solubilitate medie.
Atunci cand reactia de precipitare se produce in prezenta unei tarii ionice mari, se va tine seama de coeficientii de activitate ai ionilor prezenti in sistem (ionii precipitatului si ionii straini, daca este cazul).
Daca, totusi calculele de solubilitate se efectueaza fara sa se tina seama de taria ionica a solutiei de analizat, nu se vor inregistra erori semnificative in rezultatele analizei calitative. Nu acelasi lucru se intampla cand astfel de calcule, referitoare la solubilitate servesc la determinari cantitative.
Expresia produsului de solubilitate de mai sus este valabila pentru toate substantele formate din cationi si anioni cu aceeasi valenta.
Cand compusii respectivi sunt formati din ioni cu valente diferite, pentru deducerea expresiei produsului de solubilitate, trebuie sa se tina seama ca prin dizolvarea unei molecule de tip MnAm se formeaza n ioni Mm+ si m ioni An−, intervenind urmatorul proces de echilibru :
MnAm MnAm nMm+ + mAn (8)
faza solida solutie saturata
Aplicand acestui echilibru relatia produsului de solubilitate, se obtine :
Ps = [Mm+]n · [An−]m (9)
Deoarece nu exista substante absolut insolubile, marimea produsului de solubilitate niciodata nu este egala cu zero, ci va avea totdeauna o valoare bine definita, oricat de mica ar fi ea.
In practica de laborator, solutiile initiale sunt, de obicei, 10−2 m.
Orice precipitare incepe din momentul cand produsul concentratiilor ionilor unui electrolit in solutie devine mai mare decat produsul de solubilitate respectiv. Ionii care depasesc aceasta valoare se vor combina neincetat cu formare de precipitat.
Orice precipitare inceteaza in momentul cand relatia produsului de solubilitate este din nou nesatisfacuta. Nici o precipitare nu poate fi absolut completa, deoarece produsul de solubilitate Ps are o valoare bine definita pentru toti electrolitii greu solubili, din care motiv o parte mai mare sau mai mica din ionii precipitatului vor ramane in solutie.
Deseori concentratia ionilor ramasi in solutie este atat de mica incat nu mai perturba unele operatii ulterioare. In astfel de cazuri precipitarea se considera practic completa. In mod obisnuit un ion este practic complet precipitat dintr-o solutie, cand concentratia lui din sistem este mai mica decat 10− 6 ion-g /l.
Dizolvarea precipitatelor este tot atat de importanta pentru analiza chimica ca si formarea lor. Conform relatiei produsului de solubilitate, dizolvarea unui precipitat are loc numai atunci cand produsul concentratiei ionilor respectivi din solutie este mai mic decat produsul de solubilitate al respectivului compus.
Daca in procesul dizolvarii unui precipitat se micsoreaza concentratia din solutie (printr-un mijloc oarecare) pentru cel putin unul dintre ionii sau componentii precipitatului, solutia devine nesaturata si se dizolva o noua cantitate de precipitat, pana cand se satisface iarasi relatia produsului de solubilitate sau pana la dizolvarea totala.
1. Relatia dintre produsul de solubilitate, solubilitate si concentratia ionilor in apa "pura"
Daca se cunoaste solubilitatea molara, S (mol/l), a unui electrolit greu solubil, se poate calcula produsul de solubilitate Ps al acestuia si invers, daca se cunoaste valoarea produsului de solubilitate, se pot calcula concentratiile diferitilor ioni ai electrolitului in solutia sa saturata, precum si solubilitatea substantei.
Odata cunoscute valorile S si Ps , se pot realiza o serie de studii comparative pentru calcularea celui mai usor sau celui mai greu compus solubil. Astfel de studii comparative se realizeaza numai pe grupe sau tipuri de compusi : MA, MA2, M2A,, MnAm.
Intre solubilitatea molara si produsul de solubilitate Ps exista o permanenta corelatie, functie de tipul si natura electrolitului greu solubil studiat.
Electroliti de tip MA care disociaza dupa echilibrul :
MA Mz+ + Az− Ps = [Mz+] · [Az−] (10)
faza solida solutie saturata
Concentratiile celor doi ioni din solutie sunt egale intre ele si egale cu valoarea concentratia electrolitului din solutie, deoarece concentratia unei astfel de solutii saturate este egala cu solubilitatea substantei dizolvate si deci :
[Mz+] = [Az−] = S = ![]()
Electroliti de tipul M2A si respectiv MA2 , care disociaza :
M2A 2M+ + A2− MA2 M2+ + 2A−
faza solida solutie saturata faza solida solutie saturata
Din procesele de disociatie rezulta :
[A2−] = ![]() [M+] = S(tip M2A ) (12)
[M+] = S(tip M2A ) (12)
[M2+]
= ![]() [A−] = S(tip MA2) (13)
[A−] = S(tip MA2) (13)
Produsele de solubilitate al acestor tip de electroliti greu solubil sunt date de expresiile :
Ps = [M+]2 · [A2−] = (2S)2 · S = 4S3 (tip M2A)
Ps = [M2+] · [A−]2 = S · (2S)2 = 4S3(tip MA2)
din care rezulta : S = ![]() (mol/l) (16)
(mol/l) (16)
pentru electroliti de tip M2A si MA2.
Electroliti greu solubili de tip MA3 si M3A care participa la procesele de echilibru :
MA3(s) M3+ + 3A− M3A b M+ + 3A−
faza solida solutie saturata faza solida solutie saturata
Tinand seama de echilibrele de solubilitate :
[M3+] = ![]() [A−] = S (tip MA3)
[A−] = S (tip MA3)
[A3−] = ![]() [A3-] = S (tip M3A) (18)
[A3-] = S (tip M3A) (18)
Tinand seama de relatiile produsului de solubilitate, se obtine :
S(mol/l) = [M3+] = ![]() [A−] =
[A−] = ![]() (tip MA3) (19)
(tip MA3) (19)
S(mol/l) = [A3−] = ![]() [M+] =
[M+] = ![]() (tip M3A) (20)
(tip M3A) (20)
Electrolitii greu solubili de tip M2A3 si M3A2 unde se stabilesc urmatoarele echilibre intre faza solida si solutia saturata :
M2A3 2M3+ + 3A2− M3A2 3M2+ + 2A3−
faza solida solutia saturata faza solida solutia saturata
In cazul acestor electroliti greu solubili :
![]() [M3+] =
[M3+] = ![]() [A2−] = S(mol/l) pentru M2A3
[A2−] = S(mol/l) pentru M2A3
![]() [M2+] =
[M2+] = ![]() [A3-] = S(mol/l) pentru M3A2 (22)
[A3-] = S(mol/l) pentru M3A2 (22)
Ps = [M3+]2 · [A2−]3 = 22 · 33 · S2+3 = 108S5 (tip M2A3) (23)
Ps = [M2+]3 · [A3−]2 = 22 · 33 · S2+3 = 108S5 (tip M3A2) (24)
S = ![]() (mol/l) pentru M2A3 si M3A2 (25)
(mol/l) pentru M2A3 si M3A2 (25)
Compusi greu solubili de tip MnAm
Echilibrul de solubilitate, caracterizat de valoarea Ps, tinand seama de disocierea sarii, se scrie :
MnAm nMm+ + mAn- Ps = [Mm+]n · [An-]m
faza solida solutie saturata
Daca in solutie nu se produc fenomene secundare ( reactii de hidroliza, reactii de complexare etc), iar sarea MnAm este complet disociata(solutia fiind diluata), la dizolvarea fiecarei molecule de substanta solida trec in solutie n ioni de Mm+ si m ioni de An−, se poate scrie :
![]() [Mm+] =
[Mm+] = ![]() [An−] = S(mol/l) (27)
[An−] = S(mol/l) (27)
Ps = [Mm+]n · [An−]m = (nS)n (mS)m = nn · mm · Sn+m
S = ![]() (29)
(29)
Compusi greu solubili de tip MnNoAp
In practica analitica se intalnesc si numeroase exemple de substante greu solubile alcatuite din trei feluri de ioni, cu formula MnNoAp.
Relatia dintre solubilitate si produsul de solubilitate pentru acest tip de electroliti greu solubili, se obtine tinand seama de relatia de legatura dintre concentratia ionilor ce se formeaza la dizolvare si solubilitatea molara a electrolitului greu solubil si de relatia produsului de solubilitate.
In cazul electrolitului greu solubil MnNoAp :
S = 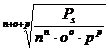 mol/l. (30)
mol/l. (30)
Principial, produsul de solubilitate se poate determina din masuratori de solubilitate ale substantelor greu solubile.
Din relatiile ce exprima legatura dintre Ps si S de mai sus, se observa ca intre valoarea solubilitatii si a produsului de solubilitate exista o corespondenta directa, numai in cazul aceluiasi tip de compusi. In cazul in care compusii sunt de tip diferit, nu intotdeauna cel care are produsul de solubilitate mai mic este mai greu solubil.
Din motive simplificatoare, unii cercetatori au propus ca in locul termenilor S si Ps sa se foloseasca :
pS = − lg S si pPs = − lg Ps (31)
1.4. Influenta ionului comun asupra solubilitatii
Se considera solutia saturata de AgCl, in prezenta fazei solide. Se poate scrie echilibrul :
AgCl(s) AgCl(solutie) Ag+ + Cl−
Daca in sistem se introduce o concentratie de ioni Cl− (de exemplu KCl), echilibrul se deplaseaza spre stanga si o parte din ionii Ag+ din solutia saturata precipita sub forma de AgCl care se adauga fazei solide. Excesul ionilor Cl− face deci mai completa precipitarea ionilor Ag+, micsorand aparent solubilitatea clorurii de argint.
Prezenta ionului comun, in exces fata de concentratia acestui ion in solutia saturata a compusului greu solubil care schimba valoarea solubilitatii acestuia. Solubilitatea molara S a compusului greu solubil, care este functie de concentratia
in solutie a ionului comun.
Pentru exemplul considerat, solubilitatea molara se poate exprimata :
S = [AgCl] + [Ag+] (33)
Tinand seama de
expresia constantei de instabilitate a clorurii de argint, A = ![]() , expresia produsului de solubilitate si
notand concentratia excesului de ioni de Cl− in solutie cu c, expresia solubilitatii molare devine :
, expresia produsului de solubilitate si
notand concentratia excesului de ioni de Cl− in solutie cu c, expresia solubilitatii molare devine :
S = ![]() +
+ ![]() =
= ![]() ( 1 +
( 1 + ![]() ) (34)
) (34)
1.5. Influenta aciditatii solutiei asupra solubilitatii
Solubilitatea compusilor greu solubili este influentata de toti factorii susceptibili de a modifica concentratiile ionice in solutia lor saturata. Dintre acesti factori, aciditatea solutiei are o mare importanta, deoarece marea majoritate a ionilor au caracter acid sau bazic si deci pot participa la reactii cu transfer de protoni, in functie de pH - ul solutiei. Echilibrul cu transfer de protoni, care transforma concentratia libera a ionului considerat, deplaseaza echilibrul eterogen de solubilitate.
Solubilitatea compusilor organici cu caracter amfolit in functie de pH
Se va considera, pentru exemplificare, 8-hidroxichinolina (oxina), compus organic cu o solubilitate redusa in apa, notata prescurtat HOx.
Oxina in stare solida, in prezenta apei, implica echilibrul eterogen :
HOx(solid) HOx(solutie) (35)
cu solubilitatea in apa pura : S0 = 10−3 mol · dm−
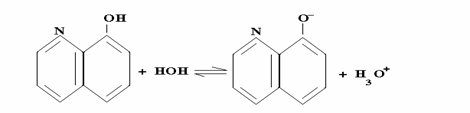
Oxina are caracter acid, conform echilibrului de mai jos :
Oxina poate avea si caracter bazic, conform echilibrului :

In functie de pH -ul solutiei, oxina din solutia saturata poate fi partial transformata in ionii oxinat si oxiniu, solubili in apa.
Solubilitatea in apa a oxinei poate fi deci scrisa sub forma :
S = [HOx] + [Ox−] + [H2Ox+]
Formarea, in masura mai mare sau mai mica, a ionilor oxinat si oxiniu este hotarata de pH - ul solutiei si evident de constantele de aciditate ale echilibrelor cu transfer de protoni :
Ka1 = 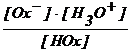 = 10−9,9 (37)
= 10−9,9 (37)
Ka2 = 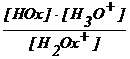 = 10−5 (38)
= 10−5 (38)
Tinand seama de aceste constante, expresia solubilitatii (36) devine :
S = 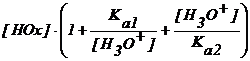
In prezenta fazei solide, solutia este saturata in oxina. Concentratia oxinei in aceasta solutie este deci egala cu S0. Expresia solubilitatii oxinei in functie de pH, poate fi scrisa deci pe baza expresiei (39), sub forma :
S = S0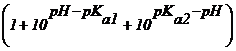
Daca compusul greu solubil are numai caracter bazic, curba solubilitate - pH, incepe cu o ramura descendenta, pana la o valoare a pH - lui apropiata de valoarea pKa, dupa care solubilitatea ramane constanta si egala cu valoarea solubilitatii in apa pura, S0. Daca dimpotriva compusul greu solubil are numai caracter acid, curba de solubilitate incepe cu un palier de ordonata S0, pana la o valoare a pH -lui apropiata de valoarea pKa, dupa care prezinta o ramura ascendenta, datorita formarii ionului bazic.
Curbele de echilibru solubilitate - pH dau o imagine sugestiva asupra existentei in sistem a diferitelor specii chimice si a zonelor de predominare a acestora in functie de pH. Cu ajutorul acestor diagrame de echilibru se pot determina cu usurinta parametrii operationali ai realizarii in conditii optime a precipitarii compusilor greu solubili cu caracter acid, bazic sau amfolit.
Solubilitatea hidroxizilor in functie de pH
Se va considera, pentru a simplifica expresiile de calcul, un hidroxid de tip BOH. De asemenea, pentru a largi interpretarea influentei pH -lui asupra solubilitatii hidroxizilor, se va considera ca acest hidroxid are caracter amfolit acid-baza.
Daca hidroxidul considerat este greu solubil, se poate scrie echilibrul eterogen :
BOH(solid) BOH(solutie), S0 = [BOH]
Hidroxidul BOH avand caracter amfolit, se pot scrie echilibrele :
BOH + H3O+ B+ + 2HOH Ka1 = ![]() (42)
(42)
BOH + HOH BO− + H3O+ Ka2 = ![]()
In solutie hidroxidul BOH este in echilibru cu speciile ionice B+ si BO−. Solubilitatea S poate fi exprimata prin :
S = [BOH] + [B+] + [BO−] (44)
Tinand seama de expresiile constantelor Ka1 si Ka2, relatia (44), se poate scrie :
S =
[BOH]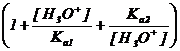 = S0
= S0![]()
Expresia solubilitatii functie de pH pentru alte tipuri de hidroxizi este diferita de expresia de mai sus si poate fi dedusa cu usurinta pe baza acelorasi rationamente.
In cazul unui hidroxid cu caracter amfoter B(OH)n se scriu ecuatiile :
B(OH)n Bn+ + nHO─ Ps = [Bn+] · [HO─]n
B(OH)n BO![]() + nH+ Ps′ = [BO
+ nH+ Ps′ = [BO![]() ] · [H+]n
] · [H+]n
S = [Bn+] + [BO![]() ] =
] = ![]() +
+ ![]()
S = ![]() + Ps′
· 10npH (49)
+ Ps′
· 10npH (49)
In multe cazuri, ultimul termen al relatiei de mai sus se poate neglija.
Solubilitatea sarurilor greu solubile in functie de pH
Daca se considera o solutie saturata a unei sari greu solubile MA, in prezenta fazei solide, se poate scrie echilibrul :
MA(s) MA(solutie) M+ + A− Ps = [M+] · [A−]
Anionul A− avand caracter bazic, participa la echilibrul cu transfer de protoni:
A−+ H3O+ HA + HOH , Ka= ![]() (51)
(51)
Daca in sistemul reprezentat prin echilibrul (50) se introduc ioni de hidrogen, deci se mareste aciditatea solutiei, anionii A− sunt protonati potrivit echilibrului (51), ceea ce are ca efect o deplasare a echilibrului de solubilitate, in sensul dizolvarii unor noi cantitati de sare BA. Procesul global este :
MA + H3O+ M+ + HA + HOH (52)
Solubilitatea sarurilor al caror anion are caracter bazic depinde deci de pH - ul solutiei.
Pentru sarea de tip MA, expresia solubilitatii in functie de pH este :
S(mol/l) = ![]() (53)
(53)
Se poate observa ca
la pH
= pKa, S = ![]() .
.
Pentru pH
< pKa, solubilitatea
sarii scade odata cu cresterea pH - lui solutiei, iar pentru pH > pKa, termenul ![]() este neglijabil in
raport cu 1 si deci : S =
este neglijabil in
raport cu 1 si deci : S = ![]() .
.
Solubilitatea precipitatelor care sunt saruri ce provin de la acizi slabi depinde de asemenea de pH - ul solutiilor.
Pentru o sare de tipul:
BmAn BmAn mBn+ + nAm-
in prezenta ionilor H+ apar o serie de specii stabile ale ionului Am-, ceea ce conduce la scaderea concentratiei acestuia si deci la deplasarea echilibrului spre dreapta, deci la cresterea solubilitatii precipitatului.
Speciile care apar sunt :
HA(m-1)- , H2A(m-2)- , H3A(m-3)- , . . . . , Hm-1 A- , HmA ,
care disociaza dupa echilibrele :
HA(m-1)- H+ + A(m)- ; ![]() =
= ![]()
H2A(m-2)- H+ + HA(m-1)- ; ![]() =
= ![]()
Hm-1
A- H+ + H(m-2) A2- ; ![]() =
= 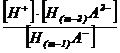
HmA H+ + H(m-1) A- ; ![]() =
= 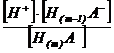
[Am-]t
= ![]() = [Am-]+[HA(m-1)-]+[H2A(m-2)-]
+ . . +[HmA]
= [Am-]+[HA(m-1)-]+[H2A(m-2)-]
+ . . +[HmA]
[Am-]t
= [Am-] + 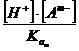 +
+ 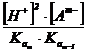 + . . +
+ . . +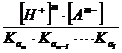 .
.
Dand factor comun [Am-] si inlocuind in produsul de solubilitate, se obtine :
S =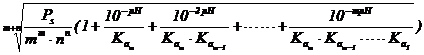
Relatia dedusa prezinta solubilitatea sarurilor in functie de produsul de solubilitate, pH - ul solutiei si de constantele de aciditate ale tuturor speciilor formate de anionul sarii cu ionul hidrogen.
In calcule se utilizeaza relatia simplificata, de forma :
S = 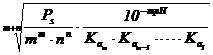
Solubilitatea sulfurilor in functie de pH
Un numar insemnat de sulfuri greu solubile sunt larg utilizate in metodele de separare analitica si de dozare gravimetrica a cationilor.
Anionul sulfurilor, S2−, are caracter bazic si deci solubilitatea sulfurilor va depinde de pH - ul solutiei.
MS(s) MS(solutie) M2+ + S2−, Ps [M2+] · [S2-] (57)
Anionii S2− pot fi protonati in functie de pH, conducand la formarea speciilor HS− si H2S. Solubilitatea molara, S, a sulfurii se scrie :
S = [M2+] = [S2−] + [HS−] + [H2S] (58)
S = [S2−]
· 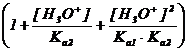 (59)
(59)
S = 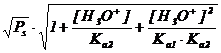 (60)
(60)
S = ![]() (61)
(61)
S = ![]() j(pH)
j(pH)
Cu ajutorul expresiei (61) se poate calcula variatia solubilitatii unei sulfuri de tip MS.
Se poate observa ca
in domeniul de pH < pKa2, solubilitatea
sulfurilor scade odata cu cresterea pH - lui, ramanand apoi constanta si egala cu ![]() pentru pH > pKa2.
pentru pH > pKa2.
Constantele pKa1 si pKa2 avand valorile 7 si respectiv 13, j(pH) devine egala cu 1 la pH > 1 Rezulta ca solubilitatea sulfurilor depinde de pH practic in toata gama normala de pH cuprinsa intre 1 si 14. Pe aceasta proprietate a sulfurilor se bazeaza utilizarea lor in separarea cationilor in grupe si subgrupe analitice.
1.6. Influenta complexarii asupra solubilitatii
Pe baza considerarii echilibrelor de precipitare ca un caz particular al echilibrelor de complexare, in care compusul complex este greu solubil, nu exista diferente fundamentale intre echilibrele :
I Ag(NH3)2+ + Hg2+ Hg(NH3)22+ + Ag+
II AgCl + I− AgI + Cl−
Pentru echilibrele I si II se pot scrie constantele :
K1 = 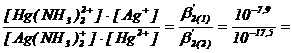 109,6 (65)
109,6 (65)
K11 = ![]() = 109,4 (66)
= 109,4 (66)
Solubilitatea sarurilor greu solubile in functie de concentratia ligandului
Se va considera, de exemplu, echilibrul de solubilitate al iodurii de argint :
AgI(s) AgI(sol.) Ag+ + I− Ps = [Ag+] · [I−]
Daca in solutie se introduce un agent de complexare X al ionilor de Ag+, se stabileste echilibrul :
Ag+ + 2X AgX2+ ![]() (68)
(68)
Cu cat complexul format, AgX2+, este mai stabil (constanta de instabilitate mai mica), cu atat concentratia ionilor Ag+ in sistem este micsorata si deci echilibrul (67) este deplasat in sensul solubilizarii iodurii de argint. Insumand echilibrele (67) si (68) se obtine echilibrul global de solubilizare a iodurii de argint sub influenta unui agent de complexare de tip X :
AgI
+ 2X AgX2+
+ I− K' = ![]() (69)
(69)
Echilibrul (69) poate fi
considerat ca un echilibru cu transfer complexant de tipul echilibrului I, unul
din complecsi fiind greu solubil. Cunoscand constantele, Ps si ![]() , se poate calcula constanta globala K' si deci se poate aprecia in ce
masura agentul de complexare X
influenteaza solubilitatea compusului greu solubil.
, se poate calcula constanta globala K' si deci se poate aprecia in ce
masura agentul de complexare X
influenteaza solubilitatea compusului greu solubil.
Echilibrul de solubilitate (69) al unui compus greu solubil prin actiunea complexanta a unui ligand poate fi deplasat in sensul solubilizarii, prin cresterea concentratiei ligandului.
Solubilitatea iodurii de argint, considerata in exemplul dat, poate fi exprimata :
![]() (70)
(70)
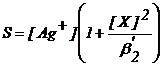
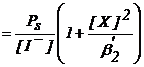 (71)
(71)
Revenind la prima egalitate din expresia (70), se poate scrie :
![]()
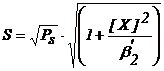 (72)
(72)
Relatia (72) reprezinta expresia solubilitatii unui compus greu solubil in functie de concentratia ligandului X.
Din relatia (72) se
poate observa ca pentru ![]() «
«![]() , solubilitatea nu este influentata de
prezenta ligandului X si
este egala cu
, solubilitatea nu este influentata de
prezenta ligandului X si
este egala cu ![]() . La o concentratie,
. La o concentratie, ![]() ,
, ![]() si creste apoi in mod insemnat cu
concentratia ligandului X, ca urmare a formarii complexului
Ag
si creste apoi in mod insemnat cu
concentratia ligandului X, ca urmare a formarii complexului
Ag![]() .
.
Intotdeauna cand se fixeaza unul dintre ionii precipitatului sub forma unei combinatii stabile, concentratia ionului in stare libera din solutie scade ceea ce determina cresterea solubilitatii precipitatului, iar daca concentratia ionului respectiv liber este redusa mult incat nu se mai atinge valoarea produsului de solubilitate, atunci fie precipitarea nu mai are loc, fie precipitatul se dizolva total.
Formarea complecsilor stabili dintre diversi liganzi si unul dintre ionii precipitatului conduce la micsorarea concentratiei ionului respectiv si deci la o marire a solubilitatii. Solubilitatea unui precipitat, in aceste conditii, este determinata atat de produsul de solubilitate, cat si de constantele de stabilitate ale complecsilor formati.
Daca se ia in considerare echilibrul de precipitare al sarii greu solubile MmNn, fara a se tine seama de sarcini :
MmNn(s) mM + nN (73)
si daca ligandul L formeaza in cationul M complecsi , ML, ML2 , . ., MLl , ce au constantele totale de stabilitate, b b , . . .. si respectiv bl , atunci in prezenta ligandului L, se fixeaza o parte din ionii M, iar solubilitatea precipitatului creste. Cand toti ionii M sunt complexati, solubilitatea precipitatului este totala.
Daca se noteaza concentratia totala in cation cu [M]t si care este egala cu mS, atunci :
![]() =
=
![]() (74)
(74)
Prin inlocuirea lui [M] in relatia produsului de solubilitate :
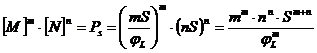 (75)
(75)
![]() (76)
(76)
Daca anionul N formeaza complecsi, atunci :
![]() (77)
(77)
Daca constantele de stabilitate b sunt foarte mici, adica complexul este usor disociabil, suma j
Formarea complecsilor stabili, ce au constante de stabilitate mari, influenteaza solubilitatea precipitatului cu atat mai mult cu cat constantele de stabilitate au valori mai mari.
Cu cat concentratia ligandului este mai mare, cu atat concentratia complecsilor este mai mare, deoarece echilibrele de complexare se deplaseaza spre formarea complecsilor, iar solubilitatea precipitatului va creste.
Ca si influenta pH -lui si efectul complexarii asupra solubilitatii precipitatelor isi gaseste aplicatii importante in procedeele de separare, prin mascarea unor ioni care ar putea sa interfere sau sa impiedice precipitarea.
Solubilitatea sarurilor greu solubile in functie de excesul ionului comun complexant
In multe cazuri ionul folosit ca agent de precipitare(ion comun) este si agent complexant, ce formeaza cu ionul supus ce se precipita, o serie succesiva de combinatii complexe, din care unele sunt solubile, astfel ca efectul total va fi acela de crestere a solubilitatii precipitatului. Urmarind reactia de precipitare, se observa ca la adaugarea reactivului, solubilitatea trece printr-un minim care corespunde formarii precipitatului, in prezenta unui mic exces de ligand(efectul ionului comun), dupa care solubilitatea creste datorita mai ales formarii unor noi specii complexe, cu ionul comun(efect de complexare).
In acest caz, pentru a calcula solubilitatea unui precipitat trebuie sa se tina seama de reactiile de complexare cu ionul comun.
Considerand un precipitat oarecare MAn , format din cationul Mn+ si anionul A− cu posibilitatea formarii unor specii cu sarcina negativa, fara a tine seama de sarcina : MA, MA2, ., MAp. Solubilitatea totala a precipitatului va fi :
S = [M] + [MA] + + [MAp] = [M](1+ b [A] + +bp[A]p) =
= [M](1+ ![]() = aM[M] = cM (78)
= aM[M] = cM (78)
Din relatia produsului de solubilitate Ps a precipitat MAn rezulta :
[M] = ![]() si S = aM
si S = aM![]()
Din relatia de mai sus se vede ca solubilitatea creste odata cu cresterea concentratiei ionului comun complexant (creste aM) dar si scade cu cresterea sa.
Pentru a obtine solubilitatea minima se face derivata, dS/d[A] = 0.
1.7. Solubilitatea hidroxizilor in prezenta agentilor complexanti
Se considera hidroxidul greu solubil MOH in sistemul :
MOH(s) MOH(sol.) M+ + OH−
In prezenta
ligandului X, care poate forma cu cationul M+ complexul MX![]() , echilibrul (80) se deplaseaza in sensul
dizolvarii precipitatului.
, echilibrul (80) se deplaseaza in sensul
dizolvarii precipitatului.
Solubilitatea hidroxidului MOH in prezenta ligandului X se poate exprima, fie in raport cu concentratia ionilor oxidril, fie in raport cu suma concentratiilor speciilor care includ ionul M+, astfel :
S ![]()
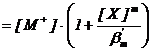 (81)
(81)
Tinand seama de expresia produsului de solubilitate a hidroxidului MOH se obtine :
S = 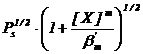 (82)
(82)
Prezenta in solutie a ligandului HO− este legata insa de concentratia ionului H3O+ prin intermediul produsului ionic al apei.
Solubilitatea hidroxidului va depinde deopotriva atat de concentratia ligandului X cat si de pH -ul solutiei.
1.8. pH - ul de precipitare al hidroxizilor in medii complexante
Se considera echilibrul de solubilitate al hidroxidului de tip M(OH)n, greu solubil :
M(OH)n(s) Mn+ + nHO− Ps = [Mn+] · [HO−]n (83)
Logaritmand cu semn schimbat relatia (83) , se obtine :
- lg Ps = - lg [Mn+] - n · lg Kw + n · lg[H3O+] (84)
Pentru 25 C, se poate scrie :
pH = ![]() =
= ![]() + constant (85)
+ constant (85)
Cu relatia (85) se poate calcula pH -ul de precipitare al cationului Mn+ sub forma de hidroxid, la diferite concentratii ale acestui cation in solutie.
Daca in solutia cationului Mn+ se introduce, inainte de precipitarea ca M(OH)n, un ligand X, susceptibil de a forma complexul MXmn+, acest fenomen micsoreaza concentratia libera a ionului Mn+, si in consecinta, pH - ul de precipitare va fi mai mare.
Echilibrul de formare a ionului complex este :
Mn+ + mX MXmn+ ![]()
Concentratia totala a ionului Mn+ din solutie este :
[Mn+]total = [Mn+] + [MXmn+] = [Mn+]total 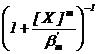
Tinand seama de (87), expresia (85) a pH -lui de precipitare a hidroxidului devine :
pH = 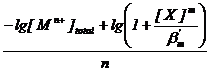 + constant (88)
+ constant (88)
pH -ul de precipitare al unui cation Mn+ sub forma de hidroxid, in prezenta unui ligand X, va fi cu atat mai mare cu cat complexul format in solutie, MXmn+ este mai stabil (bm mai mica) si de asemenea cu cat concentratia ligandului X va fi mai mare.
Cu ajutorul relatiei (88) se poate calcula pH - ul de precipitare pentru orice hidroxid metalic, in prezenta agentilor complexanti, daca se cunosc constantele de instabilitate ale complecsilor formati si produsul de solubilitate al hidroxidului.
2. Intrebari
Poate o sare sa fie relativ insolubila si totusi sa fie un electrolit tare?
Care sunt factorii ce influenteaza valoarea produsului de solubilitate?
Care sunt factorii ce influenteaza solubilitatea compusilor greu solubili ?
4. Plecand de la produsul de solubilitate Ps, care este relatia de calculare a solubilitatii molare pentru un compus greu solubil de tipul B2A ?
a) ![]() ; b)
; b) ![]() ; c)
; c) ![]() ; d)
; d) ![]() ; e)
; e) ![]()
. Plecand de la produsul de solubilitate Ps, care este relatia de calculare a solubilitatii molare pentru un compus greu solubil de tipul BA2 ?
a) ![]() ; b)
; b) ![]() ; c)
; c) ![]() ; d)
; d) ![]() ; e)
; e) ![]()
. Cunoscand produsul de solubilitate Ps, care este relatia de calculare a solubilitatii molare pentru un compus greu solubil de tipul BmAn ?
a) ![]() ; b)
; b) ![]() ; c)
; c) ![]() ; d)
; d) ![]() ; e)
; e) ![]() .
.
. Cunoscand produsul de solubilitate Ps, care este relatia de calculare a solubilitatii molare pentru un compus greu solubil de tipul B2A3 ?
a) ![]() ; b)
; b) ![]() ; c)
; c) ![]() ; d)
; d) ![]() ; e)
; e) ![]() .
.
. Cunoscand produsul de solubilitate Ps, care este relatia de calculare a solubilitatii molare pentru un compus greu solubil de tipul B3A2 ?
a) ![]() ; b)
; b) ![]() ; c)
; c) ![]() ; d)
; d) ![]() ; e)
; e) ![]() .
.
. Produsul de solubilitate al MgNH4PO4 este Ps = 2,5 ·10−1 Care este solubilitatea molara a sarii ?
a) 5,25 ·10−2 mol/l ; b) 6,33 ·10−2 mol/l ; c) 5,25 ·10−3 mol/l ;
d) ) 6,33 · 10−3 mol/l ; e) 6,33 · 10−3 mol/l .
Produsul de solubilitate al ZnS este Ps = 1,2 ·10−24. Care trebuie sa fie concentratia minima a anionului S2− pentru ca sa inceapa precipitarea ZnS dintr-o solutie de ioni Zn2+ 1·10−1 ion-g /l ?
a) 1,2 · 10−22 mol /l ; b) 1,2 ·10−24 mol/l ; c) 5,25 ·10−20 mol/l ;
d) ) 1,2 · 10−20 mol/l ; e) 5,25 · 10−21 mol/l.
In tabelul de mai jos se dau unii compusi greu solubili ai argintului, impreuna cu produsul de solubilitate Ps :
Sarea |
AgCl |
AgI |
Ag2CrO4 |
Ag2S |
Ag3PO4 |
Ag3AsO4 |
Ps |
Sub forma carei combinatii are loc precipitarea cea mai completa a ionului Ag+ ?
a) AgI ; b) Ag2S ; c) Ag2CrO4 ; d) Ag3PO4 ; e) Ag3AsO4.
Masa moleculara a unei substante greu solubile BmAn este M, iar produsul de solubilitate Ps. Care este volumul minim de apa necesar pentru a dizolva c grame substanta ?
a) ![]() litri ; b)
litri ; b) 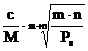 litri ; c)
litri ; c) 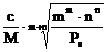 litri ;
litri ;
d) ![]() litri ; e)
litri ; e) 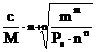 litri.
litri.
Produsul de solubilitate al bromurii de argint este 4· 10−1
. Ce valoare are solubilitatea molara a AgBr in apa " pura " ?
a) 2,51 · 10−6 mol/l ; b) 2,51 · 10−7 mol/l ; c) 6,32 · 10−6 mol/l ;
d) 6,32 · 10−7 mol/l ; e) 2,51 · 10−8 mol/l.
. Ce valoare are solubilitatea molara a AgBr in solutie NaBr 4 · 10−1 mol/l ?
a) 2,5 · 10−12 mol/l ; b) 1,0 · 10−12 mol/l ; c) 4 · 10−12 mol/l ;
b) 2,5 · 10−13 mol/l ; e) 1,0 · 10−13 mol/l.
Ce valoare are solubilitatea molara a AgBr in solutie AgNO3 2 ·10−2 mol/l ?
a) 2 · 10−14 mol/l ; b) 1,0 · 10−13 mol/l ; c) 2 · 10−12 mol/l ;
d) 2 · 10−11 mol/l ; e) 1,0 · 10−11 mol/l.
Copyright © 2025 - Toate drepturile rezervate