 | Afaceri | Agricultura | Economie | Management | Marketing | Protectia muncii |
| Transporturi |
Portofolii eficiente formate din mai mult de doua active cu risc - Frontiera Markowitz si Capital Market Line (CML)
Aplicatii rezolvate
Presupunem o
piata de capital pe care sunt
tranzactionate trei active cu risc ( ![]() ). Matricea de varianta-covarianta a activelor,respectiv
inversa acestei matrice se prezinta astfel :
). Matricea de varianta-covarianta a activelor,respectiv
inversa acestei matrice se prezinta astfel :
![]()
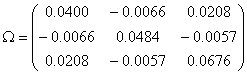 ,
, 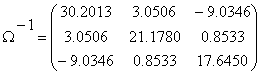
Vectorul rentabilitatilor asteptate in cazul celor trei active este
urmatorul : 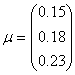 .
.
Presupunem un investitor rational care urmareste obtinerea unei rentabilitati ρ cu risc minim. Pornind de la aceasta ipoteza sa se determine :
Rezolvare
a) Reamintim faptul ca relatia risc-rentabilitate pentru portofoliile eficiente de pe frontiera Markowitz, rezulta din rezolvarea unei probleme de minim al investitorului rational, respectiv :

![]()
![]()
unde : ![]() ,
, ![]() ,
, ![]() ,
, ![]()
In cazul problemei noastre calculul indicatorilor se realizeaza astfel :

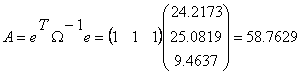
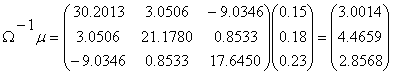
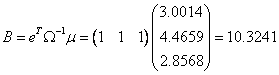

![]()
Utilizand rezultatele de mai sus putem scrie structura portofoliului eficient P , cel care asigura investitorului o rentabilitate ρ la riscul minim.

![]() , iar riscul va fi :
, iar riscul va fi : 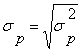
b. Pe baza relatiei dintre riscul si rentabilitatea portofoliului P prezentata mai sus putem calcula riscul portofoliilor P1 , P2, P3, P4, inlocuind rentabilitatile fixate de investitor in aceasta relatie:
![]()
![]()
![]()
|
Portofoliu |
Pi |
Pi |
|
P1 | ||
|
P2 | ||
|
P3 | ||
|
P4 |
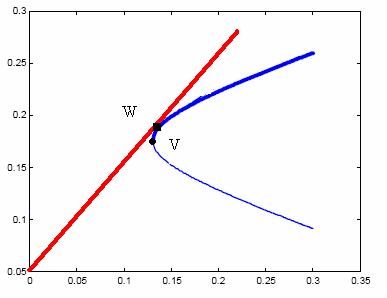
Prezentam punctele ( Pi Pi ) de mai sus in planul financiar :
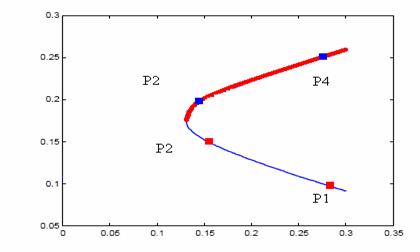
Comentarii : 1) Portofoliile formeaza o hiperbola in planul financiar, frontiera Markowitz a portofoliilor eficiente
2) P3, P4 situate pe parte superioara a hiperbolei sunt portofolii eficiente, iar P1 si P2 sunt portofolii ineficiente ( exista portofolii care la acelasi risc aduc o rentabilitate mai mare investitorului ).
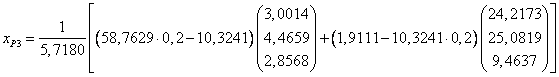
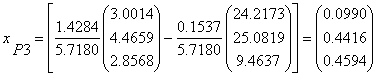
c. Folosim formulele pentru V, portofoliul cu cel mai mic risc posibil:
Structura V : ![]() Varianta:
Varianta: ![]() Rentabilitate:
Rentabilitate: ![]()
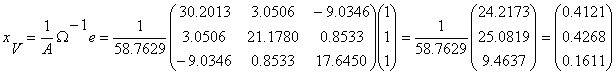
![]() , respectiv
riscul
, respectiv
riscul ![]()
![]()
Atentie !!! : portofoliul care asigura riscul minim global (V), va aduce o rentabilitate de 17.57% , investitorul asumandu-si un risc de 13.05% .
d. Notam cu W portofoliul pentru care tangenta dusa la frontiera Markowitz trece prin originea axelor.
Riscul portofoliului W rezulta din
formula :![]()
![]()
![]()
![]()
![]()
Rentabilitatea portofoliului W : ![]()
![]()
![]()
Structura portofoliului W: ![]()
![]()
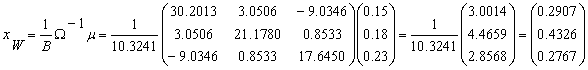 e. Reamintim faptul ca
portofoliul Z, numit conjugat al lui P, este acel portofoliu pentru care :
e. Reamintim faptul ca
portofoliul Z, numit conjugat al lui P, este acel portofoliu pentru care : ![]()
![]()
![]()
Utilizand aceasta relatie putem calcula rentabilitate portofoliului Z :
![]()
Un investitor rational poate sa formeze un portofoliu eficient P, utilizand fondurile mutuale V si W caracterizate prin :
V : 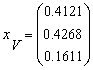 W
:
W
: 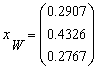
![]()
![]()
![]()
![]()
a. Sa se determine ponderea investitiei in V si W astfel incat investitorul sa obtina o rentabilitate egala cu 20%.
b. Sa se calculeze covarianta intre V si W, respectiv intre V si P, portofoliul de la punctul a).
Rezolvare :
a. Stim ca structura oricarui portofoliu eficient se poate scrie ca o combinatie convexa a portofoliilor V si W :
![]() , unde :
, unde : ![]() ,
, ![]()
Inlocuim valoarea indicatorilor si obtinem ca rezultat ponderea pe care investitorul trebuie sa o investeasca in fondurile mutuale V si W :
![]() , iar
, iar ![]()
Observatie : 1. Investitorul face short-selling pe fondul mutual V (vinde 1,5851 unitati V) si cumpara 2,5851 unitati din fondul mutual W.
2. Portofoliul W este acel portofoliu eficient care asigura cea mai mare rentabilitate daca pe piata nu exista posibilitatea de a efectua operatiuni de short-selling.
(acest lucru se realizeaza atunci cand λ este subunitar ).
Structura portofoliului P este egala cu:
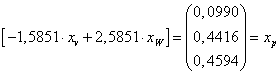
b. Covarianta intre cele doua fonduri mutuale V si W se determina astfel :
![]()
![]()
![]()
![]()
Covarianta intre fondul mutual V si portofoliul eficient P se determina astfel:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
!Atentie! Fondul mutual V, care are riscul minim global, va avea aceasi covarianta cu orice portofoliu eficient.
Pe o piata coteaza un numar de patru active financiare. Se cunosc urmatoarele informatii:
a. 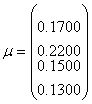 ,
, ![]()
b. ![]() ,
, ![]() ,
, ![]() ,
,
c. V : 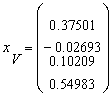 W
:
W
: 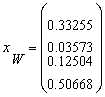
Se cere:
a. Riscurile: ![]() ,
, ![]() si rentabilitatile
si rentabilitatile ![]() ,
, ![]() .
.
b. Riscul si
rentabilitatea portofoliului P situat pe frontiera Markowitz stiind ca
rentabilitatea asteptata este ![]() .
.
c. Riscul si
rentabilitatea portofoliului Q situat pe frontiera Markowitz stiind ca riscul asumat
de investitor este ![]() .
.
d. Stiind ca ![]() sa se calculeze
rentabilitatea, riscul si structura portofoliului pietei M.
sa se calculeze
rentabilitatea, riscul si structura portofoliului pietei M.
e. Sa se
calculeze rentabilitatea, riscul si structura portofoliului S, situat pe CML
stiind ca ![]()
f. Sa se calculeze coeficientii de volatilitate![]() ,
,![]() , precum si
, precum si ![]() ,
, ![]() .
.
g. Sa se calculeze indicatorul de senzitivitate :
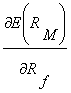 .
.
a. V: Structura
V : ![]() Varianta:
Varianta: ![]() Rentabilitate:
Rentabilitate: ![]()
![]() , respectiv
riscul
, respectiv
riscul ![]()
![]()
W: Riscul portofoliului W :![]()
![]()
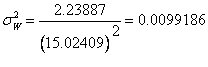
![]()
![]()
Rentabilitatea portofoliului W : ![]()
![]()
![]()
b. Riscul un portofoliu eficient de pe Frontiera Markowitz are coordonatele:
![]()
![]() (*)
(*)
Stim ca pentru portofoliul P rentabilitatea este![]() si inlocuind in formula (*) obtinem
si inlocuind in formula (*) obtinem ![]() .
.
Structura portofoliului eficient P se scrie ca o combinatie de V si W:
![]() ,
,
unde :
![]()
![]()
![]() , iar
, iar ![]()
Observatie 1. investitorul face short-selling pe fondul mutual V (vinde 16.1303 unitati V) si cumpara 17.1303 unitati din fondul mutual W.
Structura portofoliului P este :
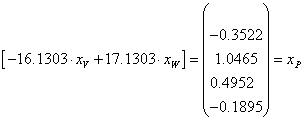
c. Se
stie ca portofoliul Q de pe frontiera Markowitz are riscul egal cu ![]() . Folosind relatia (*) obtinem:
. Folosind relatia (*) obtinem: ![]() . Rezolvand ecuatia de gradul 2 obtinem:
. Rezolvand ecuatia de gradul 2 obtinem:![]()
![]()
![]() ,
, ![]()
![]() , iar
, iar ![]()
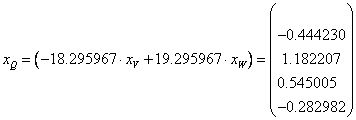
d. M: Rentabilitatea portofoliului pietei (M) este egala cu:
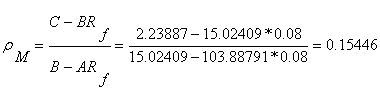
Riscul portofoliului pietei este:
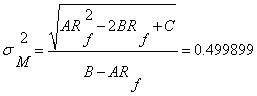
![]()
Deoarece portofoliul M se afla pe frontiera Markowitz, acesta poate fi format utilizand portofoliile V si W:
![]() , iar
, iar ![]()
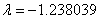 , iar
, iar ![]()
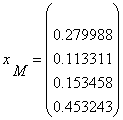 .
.
e. S: ![]()
Structura portofoliului S situat pe CML:
active cu risc: active fara risc:
![]()
![]()
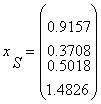
![]()
Rentabilitatea portofoliului S:
Stiind ca ecuatia dreptei CML este: ![]()
![]()
![]()
![]()
![]()
f. ![]() Modelul CAPM presupune ca:
Modelul CAPM presupune ca: ![]()
![]()
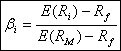
Cunoastem rentabilitatea asteptata pentru fiecare activ in parte si de aici putem sa determinam cat este coeficientul de volatilitate:
![]()
![]()
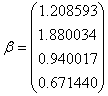
![]()
![]() ,
, ![]()
![]()
![]()
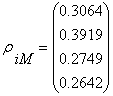
![]()
![]() ,
, ![]()
g. Stiim ca rentabilitatea asteptata a lui M este:
![]()
Astfel 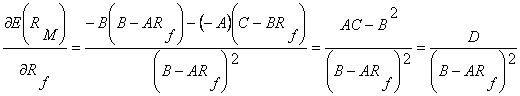
Pe o piata coteaza trei active. Se cunosc:
![]() ,
,![]()
![]()
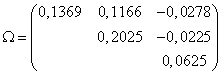
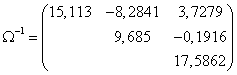
Sa se determine:
a) ecuatia frontierei Markowitz;
b) rentabilitatea, riscul si structura portofoliilor V si W;
c) riscul si structura unui portofoliu P de pe frontiera Markowitz care are
rentabilitatea ![]() ;
;
d) rentabilitatea si structura unui portofoliu Q care are riscul ![]() ;
;
e) covarianta dintre V si W si dintre V si P;
f) covarianta dintre W si P;
g) sa se calculeze indicatorii de volatilitate![]() , precum si ponderea din riscul
, precum si ponderea din riscul ![]() al fiecarui activ care
este recunoscut de piata (risc nediversificabil).
al fiecarui activ care
este recunoscut de piata (risc nediversificabil).
h) un investitor isi asuma un risc de ![]() investind in trei
fonduri mutuale: V, W,
investind in trei
fonduri mutuale: V, W, ![]() . Portofoliul P este situat pe CML. Sa se precizeze ponderile
. Portofoliul P este situat pe CML. Sa se precizeze ponderile
![]() investite in cele trei
fonduri mutuale.
investite in cele trei
fonduri mutuale.
Rezolvare :
a) ecuatia frontierei Markowitz se scrie:
![]()
Calculam A, B, C, D:
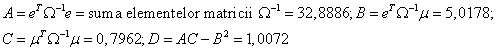
![]() Frontiera Markowitz
Frontiera Markowitz
b) ![]()
![]()
c) se foloseste ecuatia frontierei Markowitz in
care se inlocuieste ![]()
Structura lui P se scrie ca o combinatie de V si W;
![]() , iar ponderea in V este data de:
, iar ponderea in V este data de:
![]()
d) se foloseste tot frontiera Markowitz si se rezolva ecuatia de gradul II:
![]()
Se alege evident rentabilitatea mai mare adica ![]() . Structura se determina tot ca o combinatie de V si W:
. Structura se determina tot ca o combinatie de V si W: ![]()
e) 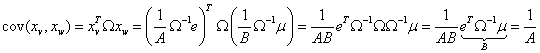
In cele de mai sus am folosit faptul ca ![]() este simetrica deci
este simetrica deci ![]() si relatia de
transpunere a produsului doua matrici oarecare X si Y
si relatia de
transpunere a produsului doua matrici oarecare X si Y 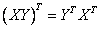 .
.
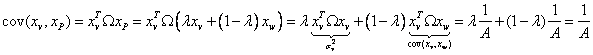
f) 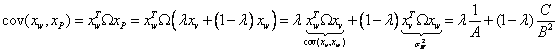
g) coeficientii de
volatilitate ![]() se determina folosind
formula:
se determina folosind
formula:
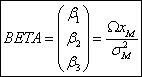 (*)
(*)
In acest scop vom calcula structura si varianta portofoliului pietei. Pentru a afla structura lui M trebuie sa calculam rentabilitatea sa folosind formula:
![]()
Determinam varianta folosind formula frontierei Markowitz, iar structura folosind descompunerea lui M in V si W.
![]()
![]() , iar
, iar 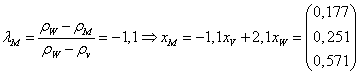
Revenim la formula (*), in care cunoastem acum toate elementele. Efectuand calculele obtinem:
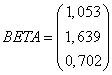
Ponderea din riscul individual recunoscut de piata
este egal cu ![]() , adica inmultim vectorul BETA cu
, adica inmultim vectorul BETA cu ![]() .
.
h) portofoliul P care se afla pe CML poate fi descompus in M si activ fara risc astfel:
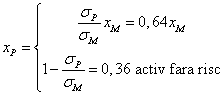
Pe de alta parte, si portofoliul M se scrie ca o combinatie de V si W cu ponderile pe care le-am determinat mai sus:
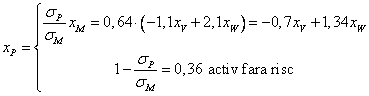
Pe o piata coteaza 2007 de active financiare
cu risc si un activ fara risc. Se estimeaza ca ecuatia frontierei Markowitz
este ![]() . Rentabilitatea activului fara risc este
. Rentabilitatea activului fara risc este ![]() .
.
a) sa se deteremine rentabilitatea asteptata si riscul portofoliului V;
b) sa se determine riscul si structura pe cele
doua fonduri mutuale V si W pentru un portofoliu de pe frontiera Markowitz care
are rentabilitatea asteptata ![]() .
.
c) cum se modifica structura (pe cele 2007 active cu risc) portofoliului de la punctul b) daca riscurile tuturor activelor cresc cu 10%.
d) sa se determine riscul si structura pe cele
doua fonduri mutuale Rf si M pentru un portofoliu de pe CML care are
renbtabilitatea asteptata ![]() .
.
e) un investitor are functia de utilitate ![]() , unde parametrul
, unde parametrul ![]() cuantifica aversiunea
la risc a investitorului. Sa se determine rentabilitatea asteptata a
portofoliului de pe frontiera Markowitz care va fi ales de catre investitor. Ce
se intampla daca
cuantifica aversiunea
la risc a investitorului. Sa se determine rentabilitatea asteptata a
portofoliului de pe frontiera Markowitz care va fi ales de catre investitor. Ce
se intampla daca ![]() ? Explicatie.
? Explicatie.
Rezolvare
Formula frontierei Markowitz se scrie astfel:
![]()
In problema frontiera Markowitz arata astfel:
![]()
Comparand relatiile obtinem:
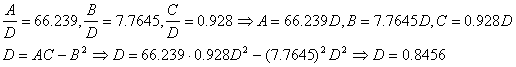
a.
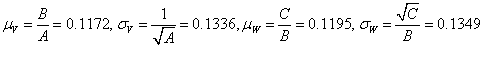
b.
![]()
![]()
c. nu se modifica!
d.
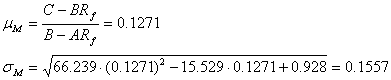
Se scrie ecuatia CML:
![]()
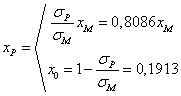
Astfel investitorul va investii 80,86% din capitalul initial in active cu risc si 19,13% in active fara risc. In aceste conditii va obtine portofoliul P care ii asigura o rentabilitate de 12,6%.
e.
Se scrie utilitatea inlocuind inlocuind varianta cu ecuatia frontierei Markowitz.
![]()
![]()
Daca ![]() , deci portofoliul ales este chiar V.
, deci portofoliul ales este chiar V.
Aplicatii propuse
Pe o piata coteaza 3 active. Se stie:
![]()
![]()
a) sa se calculeze A, B, C, D
b) sa se
calculeze ![]() si
si ![]() a unui portofoliu
situat pe frontiera Markowitz stiind ca
a unui portofoliu
situat pe frontiera Markowitz stiind ca ![]() . Stiind ca
. Stiind ca ![]() , sa se calculeze
, sa se calculeze ![]() si sa se faca un scurt
comentariu financiar.
si sa se faca un scurt
comentariu financiar.
c) stiind ca ![]() , sa se calculeze
, sa se calculeze ![]()
d) sa se
calculeze ![]() si
si ![]() a unui portofoliu
situat pe CML stiind ca
a unui portofoliu
situat pe CML stiind ca ![]() . Sa se compare
. Sa se compare ![]() . Scurt comentariu.
. Scurt comentariu.
R:
a) A=144,9275; B=18,51; C=2,442; D=11,01;
b) ![]()
c) ![]()
d)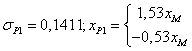
Pe o piata coteaza trei active. Se cunoaste:
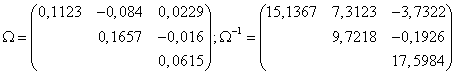
![]()
a) Sa se
calculeze: ![]()
b) Sa se calculeze
indicatorii de la punctul a) pentru cazul in care ![]() cresc cu 20%
cresc cu 20%
c) Sa se
calculeze indicatorii de la punctul a) pentru cazul in care ![]() cresc cu 20%
cresc cu 20%
d) pe baza
datelor initiale, sa se calculeze ![]() stiind ca
stiind ca ![]() , iar P este situat pe d.1. frontiera Markowitz, d.2. CML
, iar P este situat pe d.1. frontiera Markowitz, d.2. CML
R:
a) A=49,2319 B=8,80129 C=1,6104 D=1,8183
![]()
![]()
![]()
b) Cresterea tuturor rentabilitatilor cu 10% presupune modificarea vectorului de rentabilitati astfel:
![]()
In continuare vom determina felul in care se modifica A, B, C odata cu modificarea vectorului de rentablitati.
![]() - evident matricea de varianta covarianta nu se modifica in
momentul in care se modifica rentabilitatile activelor.
- evident matricea de varianta covarianta nu se modifica in
momentul in care se modifica rentabilitatile activelor.
![]()
![]()
Utilizand aceste
informatii, plus faptul ca ![]() putem determina toate
modificarile astfel:
putem determina toate
modificarile astfel:
![]()
![]()
![]()
In mod similar se obtin toate celelalte modificari.
c) se trateaza in
mod similar cu punctul b). de data aceasta, modificarea riscurilor activelor
are un impact asupra matricei de varianta covarianta si nici un impact asupra
vectorului de rentabilitati, deci ![]() .
.
Ce impact are insa asupra matricei de varianta-covarianta? Se stie faptul ca matricea de varianta covarianta poate fi descompusa astfel:

Fiecare ![]() se modifica cu 1,1 ,
deci S se modifica cu 1,1, ceea ce
inseamna ca
se modifica cu 1,1 ,
deci S se modifica cu 1,1, ceea ce
inseamna ca ![]() se modifica cu
se modifica cu ![]() , avind in vedere ca M ramane constant. In concluzie:
, avind in vedere ca M ramane constant. In concluzie:
![]()
![]()
De aici problema decurge exact ca mai sus:
![]()
![]()
![]()
![]()
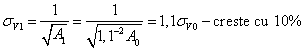
![]() s.a.m.d.
s.a.m.d.
d)
d.1. ![]()
d.2. ![]()
Pe o piata coteaza 2007 de active financiare
cu risc si un activ fara risc. Se estimeaza ca ecuatia frontierei Markowitz
este ![]() . Rentabilitatea activului fara risc este
. Rentabilitatea activului fara risc este ![]() .
.
a) sa se determine rentabilitatea asteptata si riscul portofoliului V;
b) sa se determine riscul si structura pe cele
doua fonduri mutuale V si W pentru un portofoliu de pe frontiera Markowitz care
are rentabilitatea asteptata ![]() .
.
c) cum se modifica structura (pe cele 2007 active cu risc) portofoliului de la punctul b) daca riscurile tuturor activelor cresc cu 10%.
d) sa se determine riscul si structura pe cele
doua fonduri mutuale Rf si M pentru un portofoliu de pe CML care are rentabilitatea
asteptata ![]() .
.
e) un investitor
are functia de utilitate ![]() , unde parametrul
, unde parametrul ![]() cuantifica aversiunea
la risc a investitorului. Investitorul are acces pe piata internationala unde
portofoliul pietei are rentabilitatea asteptata
cuantifica aversiunea
la risc a investitorului. Investitorul are acces pe piata internationala unde
portofoliul pietei are rentabilitatea asteptata ![]() si riscul
si riscul ![]() . Piata internationala si cea nationala nu sunt corelate. Sa
se determine rentabilitatea asteptata a portofoliului ales de investitor.
Explicatie.
. Piata internationala si cea nationala nu sunt corelate. Sa
se determine rentabilitatea asteptata a portofoliului ales de investitor.
Explicatie.
R:
a) A=55,9125 B=7,2093 C=0,9478
![]()
b) ![]()
c) nu se modifica
d) ![]()
e) se determina ![]()
se investestepe
piata nationala in portofoliul pietei 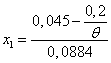 si pe piata
internationala in portofoliul pietei
si pe piata
internationala in portofoliul pietei ![]()
Pe o piata coteaza un numar de trei active. Se cunoaste:
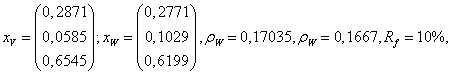
Se cere:
a) structura ![]() si rentabilitatea
si rentabilitatea ![]() a portofoliului pietei
a portofoliului pietei
b) stiind ca ![]() sa se calculeze
structura portofoliului P situat pe CML cu
sa se calculeze
structura portofoliului P situat pe CML cu ![]() .
.
Se considera o piata pe care coteaza 3 active. Matricea de varianta covarianta este:
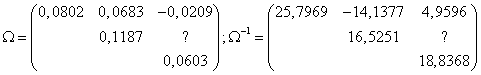
![]() ,
, ![]()
a) sa se calculeze portofoliul de frontiera Markowitz care asigura o rentabilitate de 18,5%
b) sa se
determine structura, rentabilitatea si volatilitatea unui portofoliu de CML cu
riscul ![]()
c) ca urmare a cresterii pietei, toate rentabilitatile activelor cresc cu 10%. Sa se determine modul in care se modifica rentabilitatea, riscul si structura portofoliilor V si M.
R:
![]()
![]()
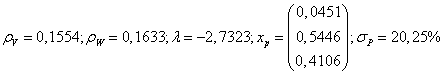
b)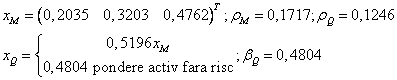
Pe o piata coteaza 4 active cu risc. Pentru frontiera Markowitz se cunosc urmatoarele elemente:
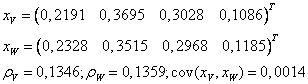
a) sa se determine structura si riscul portofoliului P cu rentabilitatea 15%
b) sa se determine
senzitivitatea riscului portofoliului P in raport cu rentabilitatea sa ![]()
c) sa se determine in ce interval trebuie sa se situeze rentabilitatea lui P astfel incat portofoliul sa aiba o componenta, respectiv 2 negative. Exista valori pentru care P are 3 componente negative?
d) sa se determine riscul, rentabilitatea si structura lui M daca Rf=7%
e) sa se precizeze in ce interval trebuie sa se situeze Rf astfel incat M sa aiba o componenta sau 2 negative.
Se considera pietele de capital din
tarile Home si Foreign. Pe piata Home ecuatia frontierei Markowitz este ![]() , iar pe piata din tara Foreign ecuatia frontierei Markowitz
este
, iar pe piata din tara Foreign ecuatia frontierei Markowitz
este ![]() . Rentabilitatea activului fara risc este aceeasi in cele
doua tari
. Rentabilitatea activului fara risc este aceeasi in cele
doua tari ![]() . Se noteaza cu V si V* portofoliul din din varful frontierei
Markowitz din tara Home, respectiv Foreign. Coeficientul de corelatie dintre
cele 2 piete de capital este 0.
. Se noteaza cu V si V* portofoliul din din varful frontierei
Markowitz din tara Home, respectiv Foreign. Coeficientul de corelatie dintre
cele 2 piete de capital este 0.
a) Sa se determine rentabilitatea asteptata si riscul celor doua portofolii V si V*;
b) Sa se determine rentabilitatea asteptata si structura pe cele doua
fonduri mutuale V si W pentru un portofoliu de pe frontiera Markowitz din tara
Home care are riscul ![]() ;
;
c) Sa se determine rentabilitatea asteptata si structura pe cele doua
fonduri mutuale ![]() si M pentru un
portofoliu de pe CML din tara Home care are riscul
si M pentru un
portofoliu de pe CML din tara Home care are riscul ![]() ;
;
d) Fie U portofoliul de risc minim care se poate construi folosind V si V*. Sa se determine structura, rentabilitatea si riscul lui U.
e) Rentabilitatile asteptate ale tuturor activelor de pe ambele piete de capital cresc cu 10%. Cum se modifica structura, riscul si rentabilitatea lui U?
f) Sa se construieasca un portofoliu eficient format din ![]() , V si V* si care are riscul
, V si V* si care are riscul ![]() .
.
R:
a) pe piata Home:
![]()
pe piata Foreign:
![]()
b) ![]()
c) ![]()
d)
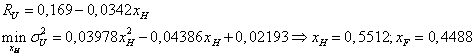
e) structura si riscul nu se modifica, iar rentabilitatea creste cu 10%.
f)![]()
Copyright © 2025 - Toate drepturile rezervate