Probleme rezolvate economie

PROBLEME REZOLVATE ECONOMIE

PROBLEMA NR.1

O societate comerciala decide majorarea capitalului social prin emisiunea de noi actiuni cu prima. Inainte de majorare bilantul societatii este urmatorul:

Bilant la data de 31.12.N

Majorarea capitalului social se face prin emiterea de 2.500 actiuni noi la o valoare de emisiune de 120 u.m./actiune. Calculati:

a) Valoarea nominala a unei actiuni;

b) Prima de emisiune pe actiune si pe total;

c) Valoarea matematica-contabila a unei actiuni inainte si dupa emisiune;

d) Valoarea teoretica a unui DS.

Rezolvare:

a) Valoarea nominala a unei actiuni (VN) se calculeaza ca raport intre capitalul social si numarul de actiuni emise:

VN =

K_S =capitalul social;

N = numarul de actiuni emise.

VN = = 100 u.m./actiune

b) Prima de emisiune reprezinta diferenta dintre valoarea (pretul) de emisiune al noilor actiuni si valoarea nominala a acestora.

P_e = V_E - VN

P_e = prima de emisiune;

V_E = valoarea de emisiune.

P_e = 120-100 = 20 u.m./actiune

Obs.

Prima de emisiune totala se calculeaza ca produs intre prima de emisiune pe actiune si numarul total de actiuni noi emise.

PE = P_e× n

n = numarul de actiuni noi emise.

PE = 20 u.m./actiune × 2.500 actiuni = 50.000 u.m.

c)  Valoarea matematica-contabila (VMC) se calculeaza ca raport intre total capitaluri proprii si numarul total de actiuni aflate in circulatie.

VMC =

1. VMC₀ (valoarea matematica-contabila inainte de majorare):

VMC = = 140 u.m./actiune

2. VMC₁ (valoarea matematica-contabila dupa majorare):

K_P = Capital social + Rezerve + Prima de emisiune totala + Alte capitaluri proprii =

=1.250.000+200.000 + 50.000 + 200.000 = 1.700.000 u.m.

VMC = = 136 u.m./actiune

d) Valoarea teoretica a dreptului de subscriere se calculeaza ca diferenta intre VMC₀ si VMC₁. Reprezinta pierderea de valoarea suferita de actiunile vechi ca urmare a emiteri noilor actiuni.

D_S = VMC₀   - VMC₁

D_s = 140 u.m./actiune - 136 u.m./actiune = 4 u.m./actiune

PROBLEMA NR. 2

Un grup de investitori decid infiintarea unei societati pe actiuni. Capitalul social ce se realizeaza in urma emisiunii este de 1.000.000 u.m. Cunoscand ca valoarea nominala a unei actiuni este de 100 u.m., determinati numarul de actiuni emise. Dupa doi ani, societatea decide majorarea capitalului social printr-o noua subscriere de actiuni, respectiv 10.000 de noi actiuni la un pret de emisiune de 200 u.m. Se cere: numarul de actiuni emise initial, prima de emisiune pe actiune si totala, precum si capitalul social dupa noua emisiune.

Rezolvare:

a) Numarul de actiuni emise (N) se calculeaza ca raport intre capitalul social si valoarea nominala a actiunilor.

N =

N = =10.000 actiuni

b) Prima de emisiune pe actiune (P_e):

P_e = V_E - VN

P_e = 200 - 100 = 100 u.m./actiuni

Prima de emisiune totala (PE):

PE = P_e×n

n = numarul de actiuni noi;

PE = 100 ×10.000 = 1.000.000 u.m.

c) Capitalul social dupa majorare (K_s'):

K_s' = (N+n)×VN

N = numarul de actiuni vechi;

n = numarul de actiuni noi;

VN = valoarea nominala.

K_s' = (10.000+10.000)×100 = 2.000.000 u.m.

PROBLEMA NR. 3

Un grup de investitori decid infiintarea unei societati pe actiuni. Capitalul social ce se realizeaza in urma emisiunii este de 50.000 u.m. si valoarea nominala a unei actiuni este de 100 u.m.,. Dupa doi ani, societatea decide majorarea capitalului social printr-o noua subscriere de actiuni, respectiv 250 de noi actiuni la un pret de emisiune de 200 u.m. Se cere:

1.numarul de actiuni emise initial : 500 actiuni

2.prima de emisiune pe actiune : 100 u.m./actiune

3.prima de emisiune totala in conditiile in care prima de emisiune pe actiune este de 100 u.m./actiune : 25.000 u.m

4.capitalul social dupa noua emisiune : 75.000 u.m.

Rezolvare:

a)Numarul de actiuni emise (N) se calculeaza ca raport intre capitalul social si valoarea nominala a actiunilor.

N =

N = = 500 actiuni

b) Prima de emisiune pe actiune (P_e):

P_e = V_E - VN

P_e = VE-VN = 200 - 100 = 100 u.m./actiune

c) Prima de emisiune totala (PE):

PE = P_e×n

PE_t = P_e×n = 100 × 250 = 25.000 u.m

d) Capitalul social dupa majorare (K_s'):

K_s' = (N+n)×VN

K_S' = (N+n)×VN = (500 + 250)×100 = 75.000 u.m.

PROBLEMA NR. 3"

Un grup de investitori decid infiintarea unei societati pe actiuni. Capitalul social ce se realizeaza in urma emisiunii este de 300.000 u.m. si valoarea nominala a unei actiuni este de 300 lei.

Dupa doi ani, societatea decide majorarea capitalului social printr-o noua subscriere de actiuni, respectiv 1.500 de noi actiuni la un pret de emisiune de 400 u.m. Se cere:

1.numarul de actiuni emise initial : 1.000 actiuni

2.prima de emisiune pe actiune : 100 u.m./actiune

3.prima de emisiune totala in conditiile in care prima de emisiune pe actiune este de 100 u.m./actiune : 150.000 u.m

4.capitalul social dupa noua emisiune : 750.000 u.m.

Rezolvare:

a)Numarul de actiuni emise (N) se calculeaza ca raport intre capitalul social si valoarea nominala a actiunilor.

N =

N = = 1.000 actiuni

b) Prima de emisiune pe actiune (P_e):

P_e = V_E - VN

P_e = VE-VN = 400 - 300 = 100 u.m./actiune

c) Prima de emisiune totala (PE):

PE = P_e×n

PE_t = P_e×n = 100 × 1.500 = 150.000 u.m

d) Capitalul social dupa majorare (K_s'):

K_s' = (N+n)×VN

K_S' = (N+n)×VN = (1.000 + 1.500) × 300 = 750.000 u.m.

PROBLEMA NR.4

Calculati valoarea de achizitie a unei cambii emise pentru o perioada de 60 zile, in conditiile unei rate de scontare de 3,6% daca valoarea sa nominala este de 1.000 u.m.

Rezolvare

Valoarea de achizitie a cambiei va rezulta prin scadere din valoarea nominala a scontului. Scontul se calculeaza astfel:

S = ,

Unde:

S = scontul;

R_S = rata scontului;

T = numarul de zile ramase pana la scadenta.

La data emiterii cambiei, cu 60 zile inainte de scadenta, scontul este urmatorul:

S = = 6 u.m.

V_a = VN - S = 1.000 u.m. - 6 = 994 u.m.

PROBLEMA NR.4

Calculati valoarea de achizitie a unei cambii emise pentru o perioada de 90 zile, in conditiile unei rate de scontare de 15% daca valoarea sa nominala este de 1.000 u.m.

Rezolvare

Valoarea de achizitie a cambiei va rezulta prin scadere din valoarea nominala a scontului. Scontul se calculeaza astfel:

S = ,

Unde:

S = scontul;

R_S = rata scontului;

T = numarul de zile ramase pana la scadenta

La data emiterii cambiei, cu 90 zile inainte de scadenta, scontul este urmatorul:

S = = = 37.5 u.m.

V_a = VN - S = 1.000 u.m. - 37.5 = 962.5 u.m.

PROBLEMA NR. 5

O societate pe actiuni isi majoreaza capitalul de la 10.000 la 15.000 actiuni, in urmatoarele conditii de emisiune:

- valoarea nominala = 1.000 u.m.,

- prima de emisiune = 100 u.m.

La bursa actiunile societatii coteaza 1.200 u.m. Valoarea teoretica a unei actiuni, inainte de majorarea capitalului era de 1.150 u.m.

Sa se stabileasca pretul platit de vechii actionari si noii actionari, care subscriu la noua emisiune, cunoscand ca la bursa drepturile de subscriere coteaza 30 u.m.

Rezolvare:

N = 10.000 actiuni;

n = 5.000 actiuni;

VN = 1.000 u.m.;

P_e = 100 u.m.;

C_b = 1.200 u.m.;

C_t0 = 1.150 u.m.;

D_Sb = 30 u.m.

C_t1 =

VE = VN+ P_e = 1.000+100 = 1.100 u.m.

C_t1 = = 1.133,33 u.m.

D_S = C_t0- C_t1 = 1.150-1.133,33 = 16,67 u.m.

- Pretul platit de un actionar vechi este:

P = VN+ P_e = 1.000+100 = 1.100 u.m.

- Pretul platit de un actionar nou este:

P' = VE+D_Sb×R_S

- Rata de subscriere

R_S = = = 2

P' = 1.100+30×2 = 1.160 u.m.

PROBLEMA NR. 6

Se cunosc urmatoarele date pentru actiunile societatilor A, B, C si D:

Cursul actiunilor u.m.

Beneficiul net pe actiune (BPA) u.m.

Dividendul net pe actiune D u.m.

Sa se calculeze randamentul dat de dividende pentru anul 2008 si coeficientul de capitalizare (PER) pentru anii 2008 si 2009.

Rezolvare:

Randamentul dat de actiune se calculeaza dupa formula:

h = ×100

Coeficientul de capitalizare PER (price earnings ratio) arata cat trebuie sa plateasca un investitor pentru o actiune pentru a obtine o unitate monetara din profiturile firmei emitente. Cand PER este mare, actiunea este scumpa; ea poate fi supraevaluata si detinerea ei nu se justifica. Cand PER este mic, actiunea este ieftina si se recomanda cumpararea acesteia.

PER =

Rezultatele obtinute pot fi prezentate astfel:

PROBLEMA NR.6

Se cunosc urmatoarele date pentru actiunile societatilor A,B,C,si D:

Cursul actiunilor u.m.

Beneficiul net pe actiune (BPA) u.m.

Dividendul net pa actiune D lei

Sa se calculeze randamentul dat de dividende pentru anul 2008 si coeficientul de capitalizare (PER) pentru anii 2008 si 2009.

Randamentul dat de actiune se calculeaza dupa formula:

h = ×100

Coeficientul de capitalizare PER (price earnings ratio) arata cat trebuie sa plateasca un investitor pentru o actiune pentru a obtine o unitate monetara din profiturile firmei emitente. Cand PER este mare, actiunea este scumpa; ea poate fi supraevaluata si detinerea ei nu se justifica. Cand PER este mic, actiunea este ieftina si se recomanda cumpararea acesteia.

PER =

Rezultatele obtinute pot fi prezentate astfel:

PROBLEMA NR. 7

O societate pe actiuni decide, dupa majorarea capitalului prin aport in numerar, majorarea capitalului sau prin incorporarea din rezerve a unei parti ce reprezinta 1.000 actiuni gratuite.

Sa se determine:

a) valoarea bilantiera a unei actiuni, inainte si dupa majorarea capitalului;

b) care este valoarea teoretica a unui Ds.

Bilantul societatii, inainte de majorarea capitalului se prezinta astfel:

Rezolvare:

a) VMC₀ = = 120 u.m

Dupa majorarea capitalului social prin incorporare de rezerve creste numarul de actiuni, insa capitalul propriu ramane acelasi.

VMC = = 112,5 u.m.

b) D_S = VMC₀- VMC₁ = 120-112,5 = 7,5 u.m.

PROBLEMA NR. 8

O societate pe actiuni isi majoreaza capitalul de la 8.000 la 10.000 actiuni, in urmatoarele conditii de emisiune:

- valoarea nominala = 700 u.m.,

- prima de emisiune = 50 u.m.

La bursa actiunile societatii coteaza 900 u.m. Valoarea teoretica a unei actiuni, inainte de majorarea capitalului era de 850 u.m.

Sa se stabileasca pretul platit de vechii actionari si noii actionari, care subscriu la noua emisiune, cunoscand ca la bursa drepturile de subscriere coteaza 28 u.m.

Rezolvare:

N = 8.000 actiuni;

n = 2.000 actiuni;

VN = 700 u.m.;

P_e = 50 u.m.;

C_b = 900 u.m.;

C_t0 = 850 u.m.;

D_Sb = 28 u.m.

C_t1 =

VE = VN+ P_e = 700+50 = 750 u.m.

C_t1 = = 830 u.m.

D_S = C_t0- C_t1 = 850-830 = 20 u.m.

- Pretul platit de un actionar vechi este:

P = VN+ P_e = 700+50 = 750 u.m.

- Pretul platit de un actionar nou este:

P' = VE+D_Sb×R_S

- Rata de subscriere:

R_S = = = 4

P' = 750+28×4 = 862 u.m.

PROBLEMA NR. 9

Fie un imprumut obligatar cu o durata de viata de 5 ani, in cadrul caruia s-au emis 100.000 obligatiuni de cate 1.000 u.m. valoare nominala. Rata nominala a dobanzii este de 8,5%. Se considera ipoteza amortizarii prin serii constante.

Sa se determine care este valoarea reala a acestui imprumut obligatar, cunoscand ca ratele dobanzii la termen, incepand din primul an pana in al cincilea sunt de 10%.

Rezolvare:

Obs.

Amortizarea prin serii constante presupune rambursarea in fiecare an a unei rate constante din imprumutul obligatar, dobanda calculandu-se la suma ramasa de rambursat.

Rata de rambursat =

VN = valoarea nominala a imprumutului obligatar;

n = numarul de ani (durata de viata a imprumutului).

Rata = = 200 u.m.

Mentiune:

Rata poate fi calculata pentru tot imprumutul sau pentru o singura obligatiune. Pentru simplificarea calculelor s-a ales varianta a doua.

Calculul dobanzii:

- pentru I an:

d₁ = VN×R_D = 1.000×8,5% = 85;

- pentru al II-lea an:

d₂ = 800×8,5% = 68;

- pentru al III-lea an:

d₂ = 600×8,5% = 51;

- pentru al IV-lea an:

d₂ = 400×8,5% = 34;

- pentru al V-lea an:

d₂ = 200×8,5% = 17;

Anuitatea reprezinta rata de rambursat plus dobanda.

A = rata + dob.

Planul de rambursare a imprumutului obligatar

Valoarea reala (V_r) a unei obligatiuni care se amortizeaza se poate determina pe baza datelor din tabelul anterior astfel:

V_r =

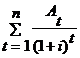
A_t = anuitatea la anul "t";

i = rata dobanzii la termen pe piata;

n = durata de viata a imprumutului (nr. ani).

V_r = ++++

V_r = ++++

V_r = 259,09+221,48+188,58+159,82+134,78 = 963,65 u.m.

Rezultatul obtinut arata ca pentru un investitor care cumpara obligatiuni, pretul de 963,65 u.m. este acoperit de fluxurile financiare viitoare, actualizate in functie de rata dobanzii pe piata. Acesta reprezinta pretul maxim ce poate fi acceptat de un investitor la subscriere.

Pentru intreg imprumutul obligatar suma ce poate fi platita la subscriere este:

V_t = 963,65×100.000 = 96.365.000 u.m.

PROBLEMA NR. 10

Care este pretul de cumparare al unei obligatiuni emisa pentru o durata de 10 ani, la o valoare nominala de 1.000 u.m., cunoscand ca rambursarea se face sub forma cuponului unic, in conditiile in care rata dobanzii la termen este de 15%?

Rezolvare:

Valoarea nominala (VN) = 1.000 u.m.;

Numar ani (n) = 10;

Rata dobanzii la termen (i) = 15%.

P_e =

P_e = = 247,18 u.m.

PROBLEMA NR. 11

Fie un imprumut obligatar cu o durata de viata de 7 ani, in cadrul caruia s-au emis 200.000 obligatiuni de cate 1.400 u.m. valoare nominala. Rata nominala a dobanzii este de 10%. Se considera ipoteza amortizarii prin serii constante.

Sa se determine care este valoarea reala a acestui imprumut obligatar, cunoscand ca ratele dobanzii la termen, incepand din primul an pana in al saptelea sunt de 12%.

Rezolvare:

Rata de rambursat =

VN = valoarea nominala a imprumutului obligatar;

n = numarul de ani (durata de viata a imprumutului).

Rata = = 200

Calculul dobanzii:

- pentru I an:

d₁ = VN×R_D = 1.400×10% = 140;

- pentru al II-lea an:

d₂ = 1.200×10% = 120;

- pentru al III-lea an:

d₂ = 1.000×10% = 100;

- pentru al IV-lea an:

d₂ = 800×10% = 80;

- pentru al V-lea an:

d₂ = 600×10% = 60;

- pentru al VI-lea an:

d₂ = 400×10% = 40;

- pentru al VII-lea an:

d₂ = 200×10% = 20;

Planul de rambursare a imprumutului obligatar

V_r =

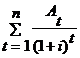
A_t = anuitatea la anul "t";

i = rata dobanzii la termen pe piata;

n = durata de viata a imprumutului (nr. ani).

V_r = ++++++

V_r = ++++++

V_r = 303,57+255,10+213,53+177,94+147,53+121,59+99,51

V_r = 1.318,77 u.m.

PROBLEMA NR. 12

Randamentul actuarial al unei obligatiuni, emisa la o valoare nominala de 15.000 u.m. pentru o durata de 10 ani si rambursabila la finalul perioadei este de 9,65%.

Sa se determine sensibilitatea "S" si durata de timp "D" in care fluxurile financiare obtinute din dobanzi compenseaza pierdere provocata de rata inflatiei, cunoscand ca valoarea reala a obligatiunii este 14.800 u.m., iar rata nominala a dobanzii de 10%.

Rezolvare

Dobanda (d)

d = VN×R_D

d = 1.500 u.m.

Planul de rambursare a imprumutului obligatar

An 1:

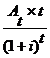= = 1.367,99

An 2:

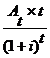= = 2.495,19

An 3:

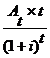= = 3.413,39

An 4:

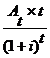= = 4.150,65

An 5:

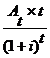= = 4.731,71

An 6:

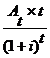= = 5.178,34

An 7:

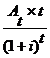= = 5.509,71

An 8:

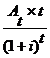= = 5.742,64

An 9:

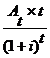= = 5.891,91

An 10:

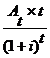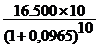= = 65.674,63

D =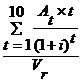

D = = 7,0375 ani;

S = -

S = -×7,0375 = -6,418

Pentru a se compensa pierderea de valoare produsa de rata inflatiei din economie (reflectata de rata dobanzii pe piata) prin incasarile anuale din dobanzi este necesara o perioada de timp mai mare de 7 ani.

Sensibilitatea indica faptul ca va scadea cursul obligatiunii cu 6,418% daca rata dobanzii creste cu 1%.

PROBLEMA NR. 13

Intocmiti planul de rambursare si determinati valoarea actuala a unui imprumut caracterizat prin rambursare in final, valoarea nominala a unei obligatiuni = 1.000 u.m., rata cuponului = 10%, scadenta = 5 ani (calculul se va face pe o obligatiune) in conditiile in care rata dobanzii la termen inregistreaza urmatoarele valori procentuale anuale: 10%, 12%, 14%, 13%, 11%.

Rezolvare:

Planul de rambursare a imprumutului obligatar

V_r =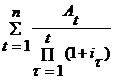

V_r =++++ +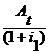

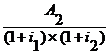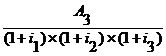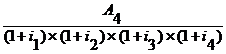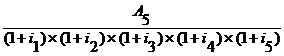
V_r = ++++

V_r = 90,91 + 81,17 + 71,20 + 63,01 + 624,42 = 929,71 u.m.

In conditiile in care prognoza referitoare la ratele dobanzii la termen pe urmatorii 5 ani se va confirma, cumparatorul unei obligatiuni va trebui sa plateasca maximum 929,71 unitati monetare.

PROBLEMA NR. 14

Un imprumut obligatar de 100.000 u.m. este divizat in 2000 obligatiuni de 500 u.m. valoare nominala fiecare. Rata nominala a dobanzii este de 10%. Jumatate din obligatiuni sunt rambursate la finele a 3 ani, iar cealalta jumatate la finele celor 4 ani. Care este pretul de subscriere al acestor obligatiuni, pentru a putea produce o rata de rentabilitate actualizata de 11%?

Rezolvare:

VN_t = 100.000 u.m.;

N = 2.000 obligatiuni;

VN = 500 u.m./obligatiune

R_d = 10%;

d₁ = 3 ani → ½ oblig.;

d₂ = 4 ani → ½ oblig.;

K = 11% (=i);

P_e = ?

Planul de rambursare a imprumutului obligatar

P_e =

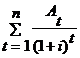
P_e = +++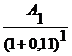

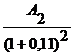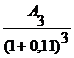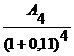
P_e = +++

P_e = 9.009 + 8.116 + 43.871 + 36.230 = 97.226 u.m.

P_e = 97.226 u.m.

P_e/oblig. = = 48,613 u.m.

PROBLEMA NR. 15

Fie un imprumut obligatar cu o durata de viata de 6 ani, in cadrul caruia s-au emis 100.000 obligatiuni de cate 1.800 u.m. valoare nominala. Rata nominala a dobanzii este de 9%. Se considera ipoteza amortizarii prin serii constante.

Sa se determine care este valoarea reala a acestui imprumut obligatar, cunoscand ca ratele dobanzii la termen, incepand din primul an pana in al saselea sunt de 10%.

Rezolvare:

Rata = = = 300 u.m.

Obs.

Pentru simplificarea calculelor s-au facut calculele pentru o singura obligatiune. Pentru tot imprumutul se va inmulti cu numarul de obligatiuni.

Dobanda:

d = VN × R_d

d₁ = 1.800×9% = 162;

d₂ = 1.500×9% = 135;

d₃ = 1.200×9% = 108;

d₄ = 900×9% = 81;

d₅ = 600×9% = 54;

d₆ = 300×9% = 27.

Planul de rambursare a imprumutului obligatar

V_r =

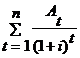
V_r = +++++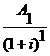

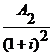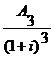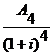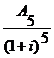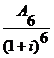
V_r = +++++

V_r = 420+359,5+306,5+260,2+219,8+184,6 = 1.750,6 u.m.

PROBLEMA NR. 16

Intocmiti tabloul de rambursare si determinati valoarea actuala a unui imprumut caracterizat prin rambursare in final, valoarea nominala a unei obligatiuni = 1.500 u.m., rata cuponului = 11%, scadenta = 4 ani (calculul se va face pe o obligatiune) in conditiile in care rata dobanzii la termen inregistreaza urmatoarele valori procentuale anuale: 12%, 14%, 16%, 14%.

Rezolvare:

Planul de rambursare a imprumutului obligatar

V_r =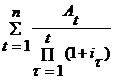

V_r = +++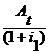

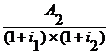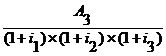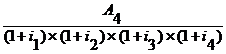
V_r = +++

V_r = 147,32+129,23+111,4+986,12 = 1.374,07 u.m.

PROBLEMA NR. 17

Un investitor cumpara 100 actiuni X la un curs de 2.450 u.m./actiune. Pana in ziua de lichidare a lunii respective, cursul actiunii va creste, iar la o data situata intre data cumpararii actiunilor si cea de lichidare cursul devine 2.600 u.m./actiune. Investitorul decide sa vanda actiunile. Care va rezultatul pentru investitor in conditiile unei taxe de negociere de 0,5%?

Rezolvare:

Valoarea tranzactiei de cumparare:

VT_c = N C_c

VT_c = 100 2.450 = 245.000 u.m.

Unde:

VT_c - valoarea tranzactiei de cumparare;

N - numar de actiuni;

C_c - curs de cumparare;

Taxa de negociere pentru tranzactia de cumparare:

TN_c = VT_c×TN

TN_c = 245.000×0,5% = 1.225 u.m.

Unde:

TN_c - valoarea taxei de negociere la cumparare;

TN - taxa de negociere (in procente);

Valoarea tranzactiei de vanzare:

VT_v = N×C_v

VT_v = 100×2.600 = 260.000 u.m.

Unde:

VT_v - valoarea tranzactiei de vanzare;

C_v - curs de vanzare;

Taxa de negociere pentru tranzactia de vanzare:

TN_v = VT_v×TN

TN_v = 260.000×0,5% = 1.300 u.m.

Unde:

TN_v - valoarea taxei de negociere la vanzare;

Rezultatul final:

Rezultatul = VT_v - VT_c - TN_c - TN_v

Rezultatul = 260.000 - 245.000 - 1.225 - 1.300 = 12.475 u.m.

PROBLEMA NR. 18

Un investitor cumpara 100 actiuni X la un curs de 2.450 u.m./actiune. Pana in ziua de lichidare a lunii respective, cursul actiunii va creste, iar la o data situata intre data cumpararii actiunilor si cea de lichidare cursul devine 2.600 u.m./actiune. Investitorul decide sa vanda actiunile. Care va rezultatul pentru investitor in conditiile unei taxe de negociere de 0,5%?

Rezolvare:

Valoarea tranzactiei de cumparare:

VT_c = N C_c

VT_c = 100 2.450 = 245.000 u.m.

Unde:

VT_c - valoarea tranzactiei de cumparare;

N - numar de actiuni;

C_c - curs de cumparare;

Taxa de negociere pentru tranzactia de cumparare:

TN_c = VT_c×TN

TN_c = 245.000×0,5% = 1.225 u.m.

Unde:

TN_c - valoarea taxei de negociere la cumparare;

TN - taxa de negociere (in procente);

Valoarea tranzactiei de vanzare:

VT_v = N×C_v

VT_v = 100×2.600 = 260.000 u.m.

Unde:

VT_v - valoarea tranzactiei de vanzare;

C_v - curs de vanzare;

Taxa de negociere pentru tranzactia de vanzare:

TN_v = VT_v×TN

TN_v = 260.000×0,5% = 1.300 u.m.

Unde:

TN_v - valoarea taxei de negociere la vanzare;

Rezultatul final:

Rezultatul = VT_v - VT_c - TN_c - TN_v

Rezultatul = 260.000 - 245.000 - 1.225 - 1.300 = 12.475 u.m.

PROBLEMA NR. 19

Un investitor detine suma de 300.000 u.m. si doreste sa achizitioneze 1.000 actiuni X la un curs de 1.100 u.m./actiune. Broker-ul practica o dobanda de 10% pe an. Sa se calculeze rezultatul tranzactiei, daca pe parcursul lunii cursul devine 1.300 u.m./actiune.

Rezolvare:

Valoarea tranzactiei de cumparare

VT_c = N×C_c

VT_c = 1.000×1.100 = 1.100.000 u.m.

Datoria la broker

DAT_B = VT_c - M

DAT_B =1.100.000-300.000 = 800.000 u.m.

Dobanda la creditul de la broker

D_CB = DAT_B×r_dob×T

D_CB = 8000.000×10%×= 6.667

Valoare tranzactiei de vanzare

VT_v = N×C_v

VT_v = 1.000×1.300 = 1.300.000 u.m.

TD = VT_c + D_CB

TD = 1.100.000 + 6.667 = 1.106.667 u.m.

TC = M + VT_v

TC = 300.000 + 1.300.000 = 1.600.000 u.m.

SFC = TC - TD

SFC = 1.600.000 - 1.106.667 = 493.333 u.m.

Inregistrarile in contul deschis la broker sunt urmatoarele:

Rezultatul final

Rezultatul final = SFC - M

Rezultatul final = 493.333 - 300.000 = 193.333 u.m.

PROBLEMA NR. 20

Un investitor detine suma de 300.000 u.m. si doreste sa achizitioneze 1.000 actiuni X la un curs de 1.100 u.m./actiune. Broker-ul practica o dobanda de 10% pe an. Sa se calculeze rezultatul tranzactiei, daca pe parcursul lunii cursul devine 1.000 u.m./actiune.

Rezolvare:

Valoarea tranzactiei de cumparare

VT_c = N×C_c

VT_c = 1.000×1.100 = 1.100.000 u.m.

Datoria la broker

DAT_B = VT_c - M

DAT_B =1.100.000-300.000 = 800.000 u.m.

Dobanda la creditul de la broker

D_CB = DAT_B×r_dob×T

D_CB = 8000.000×10%×= 6.667

Valoare tranzactiei de vanzare

VT_v = N×C_v

VT_v = 1.000×1.000 = 1.000.000 u.m.

TD = VT_c + D_CB

TD = 1.100.000 + 6.667 = 1.106.667 u.m.

TC = M + VT_v

TC = 300.000 + 1.000.000 = 1.300.000

SFC = TC - TD

SFC = 1.300.000 - 1.106.667 = 193.333 u.m.

Inregistrarile in contul deschis la broker sunt urmatoarele:

Rezultatul final

Rezultatul final = SFC - M

Rezultatul final = 193.333 - 300.000 = -106.667 u.m.

PROBLEMA NR. 21

Un investitor doreste sa cumpere 500 actiuni la un curs de 800 u.m./actiune, la termen de o luna, in conditiile unei marje de 25% si a unei dobanzi practicate de broker de 12% pe an. Sa se calculeze rata profitului obtinut de investitor stiind ca actiunile sunt vandute cu 950 u.m./actiune.

Rezolvare:

Valoarea tranzactiei de cumparare

VT_c = N×C_c

VT_c = 500×800 = 400.000 u.m.

Marja

M = VT_c × M(%)

M = 400.000×25% = 100.000 u.m.

Datoria la broker

DAT_B = VT_c - M

DAT_B = 400.000 - 100.000 = 300.000 u.m.

Dobanda la creditul de la broker

D_CB = DAT_B×r_dob×T

D_CB = 300.000 × 12% × = 3.000 u.m.

Valoare tranzactiei de vanzare

VT_v = N×C_v

VT_v = 500 × 950 = 475.000 u.m.

TD = VT_c + D_CB

TD = 400.000 + 3.000 = 403.000 u.m.

TC = M + VT_v

TC = 100.000 + 475.000 = 575.000 u.m.

SFC = TC - TD

SFC = 575.000 - 403.000 = 172.000 u.m.

Inregistrarile in contul deschis la broker sunt urmatoarele:

Rezultatul net

Rezultatul final = SFC - M

Rezultatul final = 172.000 - 100.000 = 72.000 u.m.

Rata profitului

R_p =

R_p = ×100 = 72%

PROBLEMA NR. 22

Un investitor doreste sa cumpere 700 actiuni la un curs de 330 u.m./actiune, la termen de o luna, in conditiile unei marje de 30% si a unei dobanzi practicate de broker de 10% pe an. Sa se calculeze rata profitului obtinut de investitor stiind ca actiunile sunt vandute cu 380 u.m./actiune.

Rezolvare:

Valoarea tranzactiei de cumparare

VT_c = N×C_c

VT_c = 700×330 = 231.000 u.m.

Marja

M = VT_c × M(%)

M = 231.000×30% = 69.300 u.m.

Datoria la broker

DAT_B = VT_c - M

DAT_B = 231.000 - 69.300 = 161.700 u.m.

Dobanda la creditul de la broker

D_CB = DAT_B×r_dob×T

D_CB = 161.700 × 10% × = 1.348 u.m.

Valoare tranzactiei de vanzare

VT_v = N×C_v

VT_v = 700 × 380 = 266.000 u.m.

TD = VT_c + D_CB

TD = 231.000 + 1.348 = 2312.348 u.m.

TC = M + VT_v

TC = 69.300 + 266.000 = 335.300 u.m.

SFC = TC - TD

SFC = 335.300 - 232.348 = 102.952 u.m.

Inregistrarile in contul deschis la broker sunt urmatoarele:

Rezultatul net

Rezultatul final = SFC - M

Rezultatul final = 102.952 - 69.300 = 33.652 u.m.

Rata profitului

R_p =

R_p = ×100 = 48,5%

PROBLEMA NR. 23

Un investitor cumpara 300 de actiuni la un curs de 760 u.m./actiune. Deoarece pana la sfarsitul lunii cursul scade, el realizeaza un report la cursul de compensare de 730 u.m./actiune. In luna urmatoare cursul creste, ajungand la 800 u.m./actiune. Depozitul de garantie cerut pe piata respectiva este de 30%, iar taxa de report de 12%. Care este rezultatul net al operatorului?

Rezolvare:

Valoarea tranzactiei de cumparare

VT_c = N×C_c

VT_c = 300×760 = 228.000 u.m.

Marja

M = VT_c × M(%)

M = 228.000×30% = 68.400 u.m.

Valoarea tranzactiei de report

VT_R = N×C_co

VT_R = 300×730 = 219.000 u.m.

Taxa de report

T_R = VT_R×t_rep.×T

T_R = 219.000×12%× = 2.190 u.m.

Valoare tranzactiei de vanzare

VT_v = N×C_v

VT_v = 300×800 = 240.000 u.m.

TD = VT_c + T_R

TD = 228.000 + 2.190 = 230.190 u.m.

TC = M + VT_v

TC = 68.9400 + 240.000 = 308.400 u.m.

SFC = TC - TD

SFC = 308.400 - 230.190 = 9.810 u.m.

Inregistrarile in contul deschis la broker sunt urmatoarele:

Rezultatul net

Rezultatul final = SFC - M

Rezultatul final = 78.210 - 68.400 = 9.810 u.m.

PROBLEMA NR. 24

Un investitor cumpara 500 de actiuni la un curs de 270 u.m./actiune. Deoarece pana la sfarsitul lunii cursul scade, el realizeaza un report la cursul de compensare de 250 u.m./actiune. In luna urmatoare cursul creste, ajungand la 300 u.m./actiune. Depozitul de garantie cerut pe piata respectiva este de 25%, iar taxa de report de 10%. Care este rezultatul net al operatorului?

Rezolvare:

Valoarea tranzactiei de cumparare

VT_c = N×C_c

VT_c = 500×270 = 135.000 u.m.

Marja

M = VT_c × M(%)

M = 135.000×25% = 33.750 u.m.

Valoarea tranzactiei de report

VT_R = N×C_co

VT_R = 500×250 = 125.000 u.m.

Taxa de report

T_R = VT_R×t_rep.×T

T_R = 125.000×10%× = 1.042 u.m.

Valoare tranzactiei de vanzare

VT_v = N×C_v

VT_v = 500×300 = 150.000 u.m.

TD = VT_c + T_R

TD = 135.000 + 1.042 = 136.042 u.m.

TC = M + VT_v

TC = 33.750 + 150.000 = 183.750 u.m.

SFC = TC - TD

SFC = 183.750 - 136.042 = 47.708 u.m.

Inregistrarile in contul deschis la broker sunt urmatoarele:

Rezultatul net

Rezultatul final = SFC - M

Rezultatul final = 47.708 - 33.750 = 13.958 u.m.

PROBLEMA NR. 25

Pentru actiunile societatii X s-au transmis urmatoarele ordine:

Cursul de inchidere al sedintei precedente a fost de 6.800.

Sa se calculeze: volumul maxim de actiuni tranzactionate, cursul de echilibru, coeficientii de executie al ordinelor de cumparare si, respectiv, de vanzare.

Rezolvare:

CMB_c - cel mai bun curs la cumparare

CMB_v - cel mai bun curs la vanzare

Volumul maxim de actiuni tranzactionate = 880

Cursul de echilibru = 6.850

Coeficientul de executie a ordinelor de cumparare

CE_c = ×100

OMT - ordine maxime tranzactionate;

OMP_C - ordine maxime primite la cumparare;

CE_c = ×100 = 66,16%

Coeficientul de executie a ordinelor de cumparare

CE_v = ×100

OMT - ordine maxime tranzactionate;

OMP_v - ordine maxime primite la vanzare;

CE_v = ×100 = 61,11%

2. PROBLEME PROPUSE

PROBLEMA NR.1

O societate decide majorarea capitalului social prin emisiunea de noi actiuni cu prima. Inainte de majorare bilantul societatii este urmatorul:

Bilant la data de 31.12.N

Majorarea capitalului social se face prin emiterea de 2000 actiuni noi la o valoare de emisiune de 120 u.m./actiune. Calculati:

a) Valoarea nominala a unei actiuni;

b) Prima de emisiune pe actiune si pe total;

c) Valoarea matematica-contabila a unei actiuni inainte si dupa emisiune;

d) Valoarea teoretica a unui DS.

PROBLEMA NR. 2

Un grup de investitori decid infiintarea unei societati pe actiuni. Capitalul social ce se realizeaza in urma emisiunii este de 7.000.000 u.m. Cunoscand ca valoarea nominala a unei actiuni este de 250 u.m, determinati numarul de actiuni emise. Dupa trei ani, societatea decide majorarea capitalului social printr-o noua subscriere de actiuni, respectiv 5.600 de noi actiuni la un pret de emisiune de 300 u.m. Se cere: numarul de actiuni emise initial, prima de emisiune pe actiune si totala, precum si capitalul social dupa noua emisiune.

PROBLEMA NR. 3

Un grup de investitori decid infiintarea unei societati pe actiuni. Capitalul social ce se realizeaza in urma emisiunii este de 3.000.000 u.m. Cunoscand ca valoarea nominala a unei actiuni este de 300 lei, determinati numarul de actiuni emise. Dupa doi ani, societatea decide majorarea capitalului social printr-o noua subscriere de actiuni, respectiv 10.000 de noi actiuni la un pret de emisiune de 400 u.m. Se cere: numarul de actiuni emise initial, prima de emisiune pe actiune si totala, precum si capitalul social dupa noua emisiune.

PROBLEMA NR.4

Calculati valoarea de achizitie a unei cambii emise pentru o perioada de 90 zile, in conditiile unei rate de scontare de 15% daca valoarea sa nominala este de 1.000 u.m.

PROBLEMA NR. 5

O societate pe actiuni isi majoreaza capitalul de la 25.000 la 30.000 actiuni, in urmatoarele conditii de emisiune:

- valoarea nominala = 1.000 u.m.,

- prima de emisiune = 200 u.m.

La bursa actiunile societatii coteaza 1.500 u.m. Valoarea teoretica a unei actiuni, inainte de majorarea capitalului era de 1.500 u.m.

Sa se stabileasca pretul platit de vechii actionari si noii actionari, care subscriu la noua emisiune, cunoscand ca la bursa drepturile de subscriere coteaza 550 u.m.

PROBLEMA NR.6

Se cunosc urmatoarele date pentru actiunile societatilor A,B,C,si D:

Cursul actiunilor u.m.

Beneficiul net pe actiune (BPA) u.m.

Dividendul net pa actiune D lei

Sa se calculeze randamentul dat de dividende pentru anul 2008 si coeficientul de capitalizare (PER) pentru anii 2008 si 2009.

PROBLEMA NR. 7

O societate pe actiuni decide, dupa majorarea capitalului prin aport in numerar, majorarea capitalului sau prin incorporarea din rezerve a unei parti ce reprezinta 2.000 actiuni gratuite.

Sa se determine:

a) valoarea bilantiera a unei actiuni, inainte si dupa majorarea capitalului;

b) care este valoarea teoretica a unui Ds.

Bilantul societatii, inainte de majorarea capitalului se prezinta astfel:

PROBLEMA NR. 8

O societate pe actiuni isi majoreaza capitalul de la 4.000 la 5.000 actiuni, in urmatoarele conditii de emisiune:

- valoarea nominala = 200 u.m.,

- prima de emisiune = 40 u.m.

La bursa actiunile societatii coteaza 275 u.m. Valoarea teoretica a unei actiuni, inainte de majorarea capitalului era de 270 u.m.

Sa se stabileasca pretul platit de vechii actionari si noii actionari, care subscriu la noua emisiune, cunoscand ca la bursa drepturile de subscriere coteaza 75 u.m.

PROBLEMA NR. 9

Fie un imprumut obligatar cu o durata de viata de 4 ani, in cadrul caruia s-au emis 60.000 obligatiuni de cate 1.000 u.m valoare nominala. Rata nominala a dobanzii este de 13%. Se considera ipoteza amortizarii prin serii constante.

Sa se determine care este valoarea reala a acestui imprumut obligatar, cunoscand ca ratele dobanzii la termen, incepand din primul an pana in al cincilea sunt de 17%.

PROBLEMA NR. 10

Care este pretul de cumparare al unei obligatiuni emisa pentru o durata de 5 ani, la o valoare nominala de 1.000 u.m., cunoscand ca rambursarea se face sub forma cuponului unic, in conditiile in care rata dobanzii la termen este de 15%?

PROBLEMA NR. 11

Fie un imprumut obligatar cu o durata de viata de 5 ani, in cadrul caruia s-au emis 20.000 obligatiuni de cate 2.000 u.m. valoare nominala. Rata nominala a dobanzii este de 12%. Se considera ipoteza amortizarii prin serii constante.

Sa se determine care este valoarea reala a acestui imprumut obligatar, cunoscand ca ratele dobanzii la termen, incepand din primul an pana in al saptelea sunt de 13,5%.

PROBLEMA NR. 12

Randamentul actuarial al unei obligatiuni, emisa la o valoare nominala de 10.000 u.m. pentru o durata de 6 ani si rambursabila la finalul perioadei este de 10%.

Sa se determine sensibilitatea "S" si durata de timp "D" in care fluxurile financiare obtinute din dobanzi compenseaza pierdere provocata de rata inflatiei, cunoscand ca valoarea reala a obligatiunii este 9.000 u.m, iar rata nominala a dobanzii de 11%.

PROBLEMA NR. 13

Intocmiti planul de rambursare si determinati valoarea actuala a unui imprumut caracterizat prin rambursare in final, valoarea nominala a unei obligatiuni = 5.000 u.m., rata cuponului = 13%, scadenta = 4 ani (calculul se va face pe o obligatiune) in conditiile in care rata dobanzii la termen inregistreaza urmatoarele valori procentuale anuale: 17%, 14%, 13%, 15%.

PROBLEMA NR. 14

Un imprumut obligatar de 500.000 u.m. este divizat in 5.000 obligatiuni de 100 u.m. valoare nominala fiecare. Rata nominala a dobanzii este de 8%. Jumatate din obligatiuni sunt rambursate la finele a 2 ani, iar cealalta jumatate la finele celor 4 ani. Care este pretul de subscriere al acestor obligatiuni, pentru a putea produce o rata de rentabilitate actualizata de 10%?

PROBLEMA NR. 15

Fie un imprumut obligatar cu o durata de viata de 5 ani, in cadrul caruia s-au emis 20.000 obligatiuni de cate 5.000 u.m. valoare nominala. Rata nominala a dobanzii este de 12%. Se considera ipoteza amortizarii prin serii constante.

Sa se determine care este valoarea reala a acestui imprumut obligatar, cunoscand ca ratele dobanzii la termen, incepand din primul an pana in al cincilea sunt de 13%.

PROBLEMA NR. 16

Intocmiti tabloul de rambursare si determinati valoarea actuala a unui imprumut caracterizat prin rambursare in final, valoarea nominala a unei obligatiuni = 1.500 u.m, rata cuponului = 25%, scadenta = 5ani (calculul se va face pe o obligatiune) in conditiile in care rata dobanzii la termen inregistreaza urmatoarele valori procentuale anuale: 30%, 29%, 27%, 25%, 26%.

PROBLEMA NR. 17

Un investitor cumpara 200 actiuni X la un curs de 3.500 u.m./actiune. Pana in ziua de lichidare a lunii respective, cursul actiunii va creste, iar la o data situata intre data cumpararii actiunilor si cea de lichidare cursul devine 4.000 u.m./actiune. Investitorul decide sa vanda actiunile. Care va rezultatul pentru investitor in conditiile unei taxe de negociere de 0,8%?

PROBLEMA NR. 18

Un investitor cumpara 500 actiuni X la un curs de 1.400 u.m./actiune. Pana in ziua de lichidare a lunii respective, cursul actiunii va creste, iar la o data situata intre data cumpararii actiunilor si cea de lichidare cursul devine 1.600 u.m./actiune. Investitorul decide sa vanda actiunile. Care va rezultatul pentru investitor in conditiile unei taxe de negociere de 0,6%?

PROBLEMA NR. 19

Un investitor detine suma de 500.000 u.m. si doreste sa achizitioneze 1.100 actiuni X la un curs de 1.300 u.m./actiune. Broker-ul practica o dobanda de 15% pe an. Sa se calculeze rezultatul tranzactiei, daca pe parcursul lunii cursul devine 1.500 u.m./actiune.

PROBLEMA NR. 20

Un investitor detine suma de 600.000 u.m. si doreste sa achizitioneze 1.200 actiuni X la un curs de 1.400 u.m./actiune. Broker-ul practica o dobanda de 10% pe an. Sa se calculeze rezultatul tranzactiei, daca pe parcursul lunii cursul devine 1.250 u.m./actiune.

PROBLEMA NR. 21

Un investitor doreste sa cumpere 750 actiuni la un curs de 500 u.m./actiune, la termen de o luna, in conditiile unei marje de 25% si a unei dobanzi practicate de broker de 10% pe an. Sa se calculeze rata profitului obtinut de investitor stiind ca actiunile sunt vandute cu 650 u.m./actiune.

PROBLEMA NR. 22

Un investitor doreste sa cumpere 300 actiuni la un curs de 930 u.m./actiune, la termen de o luna, in conditiile unei marje de 28% si a unei dobanzi practicate de broker de 11% pe an. Sa se calculeze rata profitului obtinut de investitor stiind ca actiunile sunt vandute cu 980 u.m./actiune.

PROBLEMA NR. 23

Pentru actiunile societatii X s-au transmis urmatoarele ordine:

Cursul de inchidere al sedintei precedente a fost de 7.200.

Sa se calculeze: volumul maxim de actiuni tranzactionate, cursul de echilibru, coeficientii de executie al ordinelor de cumparare si, respectiv, de vanzare.

PROBLEMA NR. 24

Pentru actiunile societatii X s-au transmis urmatoarele ordine:

Cursul de inchidere al sedintei precedente a fost de 11.500.

Sa se calculeze: volumul maxim de actiuni tranzactionate, cursul de echilibru, coeficientii de executie al ordinelor de cumparare si, respectiv, de vanzare.

PROBLEMA NR. 25

Pentru actiunile societatii X s-au transmis urmatoarele ordine:

Cursul de inchidere al sedintei precedente a fost de 13.500 u.m.

Sa se calculeze: volumul maxim de actiuni tranzactionate, cursul de echilibru, coeficientii de executie al ordinelor de cumparare si, respectiv, de vanzare.