 | Afaceri | Agricultura | Economie | Management | Marketing | Protectia muncii |
| Transporturi |
EVOLUTIA PROCESELOR ECONOMICE IN DECURSUL TIMPULUI
SI PROBLEMA TENDINTEI GENERALE
In perspectiva econometriei problema evolutiei proceselor economiei in timp intereseaza datorit urmatoarelor motive
- masurarea rolului unor factori calitativi (nenumerici) care isi desfasoara actiunea in decursul timpului (progresului tehnic, acumularile de bunuri, procesele de invatare, etc) poate fi abordata luand in calcul variabila timp privita ca un sir de numere in progresie aritmetica;
- actiunea unor cauze nu afecteaza instantaneu variabila-efect, ci dupa un interval de timp (lag) mai mult sau mai putin indelungat. De aici interesul dintre evolutia unor variabile-semnal (variabile precursoare) si modificare variabila-efect, intarzierea la care apar implucatiile economice generate de masurile guvernamentale;
- evidentierea invariatilor (tendinta evolutiva, oscilatiile sistematice) in sensul masurarii intensitatii acestora si modelarii rolului lor in evolutia viitoare a procesului economic.
1. Notinui specifice analizei seriilor cronologice
Analiza seriilor cronologice reprezinta un domeniu distinct in instruirea economistului intrat relativ recent in sfera de preocupari a econometriei. Ca urmare, intalnim un ansamblu de notiuni specifice, intre care frecvent utilizate sunt urmatoarele:
- seria cronologica (de timp, dinamica) - secventa de niveluri ordonate in raport cu succesiunea perioadelor (momentelor de timp). Notam astfel de niveluri cu yt, t=1, 2, n;
- analiza seriilor cronologice - metoda generala de caracterizare a seriei cronologice din perspectiva componentelor sistematice sau aleatoare in vederea masurarii intensitatii si continuitatii lor, asa incat procesul analizat din perspectiva tenporala sa devina predictibil. In raport cu scopul urmarit analiza recurge la diverse metode specifice: medii mobile, indice de sezonalitate, metodele stochastice, etc;
- cronograma - reprezentarea grafica destinata descrierii evolutiei unui fenomen in decursul timpului. In acest scop este utilizat un sistem de axe rectangulare intre care axa orizontala este rezervata "evolutiei" timpului (variabila independenta) ca o succesiune de perioade momente ordonate, iar axa verticala este destinata masurarii procesului economic reprezentat;
- tendinta generala (trend) - evolutie in timp a fenomenului analizat exprimata intr-o forma stilizata care retine aspectul general, de crestere, respectiv de descrestere neafectat de abaterile temporare;
- sezonalitate - evolutie manifestata prin oscilatii repetabile ca sens si amploare, fie in jurul tendintei, fie in jurul unui nivel mediu, urmare a unor factori care revin periodic la intervale mai mici de 1 an;
- lag - intarziere, exprimata in unitati de timp, intre modificarea variabilei cauzale si manifestarea efectului.
2. Modelul liniar unifactorial si calculul tendintei generale
Intre formele de prezentare a evolutiei in decursul timpului a unei varibile economice (poate fi consumul, exportul, cotatia la bursp, etc) statistica descriptiva recomanda seria cronologica redata sub forma unui tabel cu date (tabelul nr. 1.) dar, mai ales, reprezentarea grafica (cronograma - fig. 1).
Tabelul 1
|
Anul | |||||||||||||
|
Trim. |
I |
II |
III |
IV |
I |
II |
III |
IV |
I |
II |
III |
IV |
I |
|
yt | |||||||||||||
|
t | |||||||||||||
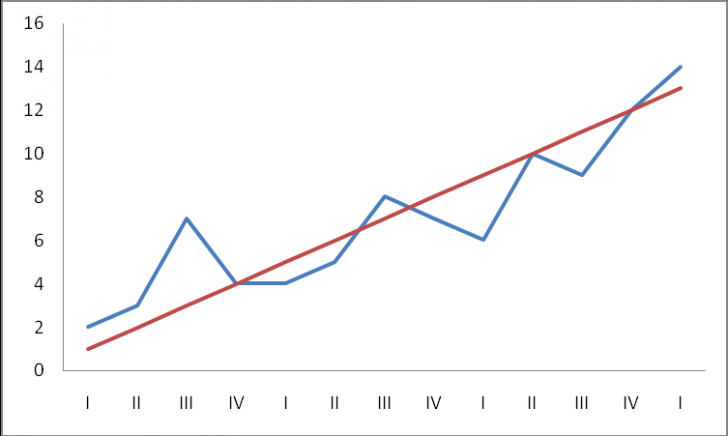
Fig. 1.
Atat datele inscrise in tabel cat si reprezentarea lor grafica evidentiaza un fel de "parteneriat" intre fenomenul analizat si succesiunea perioadelor de timp. Astfel, putem constata ca pe masura ce trece timpul, amploarea fenomenului, in general, creste. La fel de bine am putea cosntata an diverse alte situatii ca, in general, fenomenul descreste in intensitate in decursul timpului. Acestea ar fi cele 2 tendinte de baza. Intr-un astfel de parteneriat variabila independenta nu poate fi decat timpul, intrucat perioadele se succed indiferent de ceea ce se intampla in economie. Constatarea cu privire la faptul ca fenomenul analizat ia amploare pe masura ce trece timpul indica o relatie de tip liniar in care locul variabilei independente (notata cu xi in modelul liniar unifactorial 2.1.) revine factorului timp (t), dupa cum urmeaza
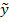
unde 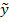
t=unitati de timp, de perioada egala, prezenrand o succesiune ordonata pe scara timpului.
Afirmam ca "amploarea fenomenului, in general, creste", respectiv, "in general fenomenul descreste", ceea ce presupune ca exista abateri de la ce este valabil in general. Astfel de abateri s-ar datora unor influente de alta natura decat cele care imprima tendinsa evolutiva. Pentru inceput, astfel de influente perturbatoare asupra tendintei le notam cu ut. Modelul (1) devine:
yt=a+bt+ut (2)
Variabila timp, introdusa in cele doua modele prin simbolul t presupune rezolvarea unor probleme de intelegere dar si de masurare:
- timpul poate fi luat in considerare drept autentic factor daca avem in vedere: cresterea cuantumului dobanzii prin capitalizare, cresterea gradului de uzura fizica si morala. Mult mai frecventa este acceptarea timpului sub forma unei variabile - repretentant pentru o serie de cauze de natura cantitativa sau calitativa, conditii de desfasurare, etc. care fie sunt prea putin cunoscute, fie sunt dificil de cuantificat, dar care, toate, actioneaza in timp intr-o oarecare directie care imprima procesului analizat o directie evolutiva constanta;
- masurarea timpului este o conditie
obligatorie pentru ca modelul (1) sa devina operational.
Intrucat timpul creste cu un spor constant egal cu 1 (o luna, un
trimestru, un an), exprimarea sa numerica poate fi reprezentata de
sirul numerelor naturale t=1, 2,
3, n-1, n dar si de sirul t=-3,
-2, -1, 0, 1, 2, 3 (pentru n impar) respectiv t=-2,5 ,-1,5, -0,5, 0,5, 1,5, 2,5 (pentru n par). Aceste din
urma variante conduc la 
In relatia (1)
variabila timpt (t) a luat locul factorului X din modelul unifactorial (2.1).
in vederea estimarii parametrilor a, b din yt=a+bt+ut,
aplicam metoda celor mai mici patrate, ceea ce implica 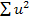
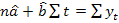
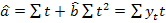
se amplifica, in situatiile in care
numerotarea timpului include marimi negative si pozitive, simetric
situate in jurul unui pivot central si care cresc cu un spor egal cu 1,
intrucat in (3, 4) 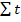
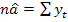
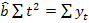
ceea ce conduce la urmatoarele relatii de estimare:
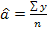
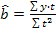
Interpretarea
estimatiilor: a - media nivelurilor yt in segmentul de timp
considerat; b - cu cat se modifica, an medie yt la
adaugarea unei unitati sirului de marimi care exprima
timpul. Daca, de exemplu, unitatea de timp t este trimestrial, atunci 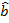
Daca atribuim valori timpului in afara celor n unitati sau perioade pentru care avem date (yt), putem obtine pe baza modelului (1), in urmna estimarii, niveluri estrapolare ale tendintei. Ele pot fi considerate drept predictii privind procesul analizat (y) daca acceptam continuitatea conditiilor (cauzelor, imprejurarilor) care au imprimat tendinta procesului.
In cele ce urmeaza,
exemplificam determinarea si extrapolarea tendintei generale (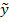
- Aspectul general de tip liniar al evolutiei descrise de cronograma (fig 1);
- Existenta unui numar impar de trimestre, ceea ce ne permite sa atribuim timpului nivelurile mentionate pe randul t al tabelului 2;
- Calculul
produselor y*t dar si t2 precum si obtinerea sumelor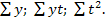
Tabelul 2
|
Anul | |||||||||||||
|
Trim. |
I |
II |
III |
IV |
I |
II |
III |
IV |
I |
II |
III |
IV |
I |
|
yt | |||||||||||||
|
t | |||||||||||||
|
t2 |
|
||||||||||||
|
yt | |||||||||||||
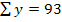
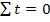
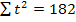
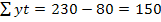
Rezulta
estimatiile: 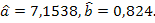
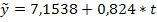
Rezulta 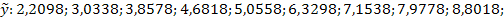
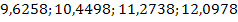
valori extrapolate privind tendinta:
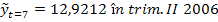
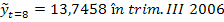
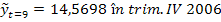
Comentarii:
- Nivelul mediu exprimat de ordonata la origine este 7,1538 pe trimestru;
- Panta exprimata de 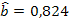
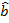
- Extrapolarile 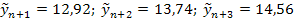
In afara tendintelor (tendinte liniare de crestere, respectiv de descrestere) pot fi constatate si evolutii mai putin rigide, exprimate prin functii neliniare. Redim in continuare o serie de situatii care pot conduce la functii polinomiale de grad mai mare decat 1, functii logaritmice, etc., mentionand functia indicata, transformarea liniara a acesteia (in paranteza), prtecum si valorile atribuite variabilei timp.
-Cererea (de produse, de credite, de valuta, etc)
y=a+b*logt+u t=1, 2, 3, , n (9)
Se apropie de un prag de saturatie (y=a+bz, unde z=logt) sau
logy=a+b*logt+u (10)
(w=a+bz unde w=logy, z =logt);
-Tendinta se indreapta spre un nivel extrem (maxim sau minim) dupa care isi schimba directia. Cazuri: vanzarile in etapa III-IV din viata produsului, evolutia PIB in anumite intervale, evolutia cotatiei la bursa sau pe piata valutarp, etc.
y=a+bt+ct2+u (11)
(y=a+bt+cz+u, unde z=t2) t=-3, -2, , 0, 1, 2, 3, ;
-Involutia tinde spre un prag limita. Cazuri: descresterea ratei somajului
y=a+b
(t=1, 2, 3, )
y=a+bk,
unde k=
-Curba logistica si succesiunea de tendinte.
Cazuri: - evolutia vanzarilor unui produs pe parcursul "vietii" acestuia; - evolutia numarului populatiei unei tari pe o durata indelungata de timp; - evolutia productivitatii muncii in conditiile adoptarii unei noi tehnologii
Tendinta generala poate fi calculata si prin alte metode decat MCMMP, precum: mediile mobiel, modificarea medie absoluta sau relativa (sporul mediu, indicele mediu) etc.
3. O clasificare a seriilor cronologice in raport cu existenta sau inexistenta tendintei generale
Din perspectiva existentei sau inexistentei tendintei in evolutia seriei de timp deosebim:
-Seria stationara - caracterizata prin oscilatii, mai mult sau mai putin intamplatoare, ca marime si directie, in jurul unui nivel de referinta - media.
O serie stationara este rezultatul unui proces stochastic stationar pentru care media si dispersia sunt constante, indiferent de momentul de la care consideram ca incepe seria. Deseori o astfel de serie cronologica este asociata unei stari de echilibru relativ.
Procesele stochastice stationare au unele proprietati utile analizei precum: posibilitatea de a determina media, dispersia covarianta pe baza unui esantion, posibilitatea descoperirii in oscilatii sinusoidale, etc.
-Seria nestationara - care prezinta tendinta de crestere sau de scadere, ceea ce face yt sa difere, functie de momentul de la care consideram ca incepe seria. Dispersia, eventual covariatia, pot fi si ele dependente de timp.
Tendinta specifica seriei nestationare poate fi:
-De tip determinist - fiind invariabila pe un interval mare de timp atat ca directie cat si ca panta. O astfel de tendinta este usor de previzut, asa incat valorile extrapolare satisfac din perspectiva preciziei.
-De tip stochastic - in sensul ca pe segmente de timp, dispuse in succesiune, poate prezenta unele modificari, indeosebi in ce priveste panta.
Deseori in modelare se urmareste izolarea tendintei generale in vederea analizei fluctuatiilor sistematice (sezonalitatea, analiza spectrala) sau in vederea analizei propagarii abaterilor de la tendinta (modelele stochastice de prognoza). In raport cu modalitatea recomandata in vederea eliminarii tendintei, deosebim:
-seria nestationara de tip T.S.P. (trend stationary
processes) pentru care trendul se recomanda sa fie eliminat prin
scadere y=(yt-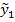
-seria nestationara de tip D.S.P. (difference stationary
processes) pentru care trendul se elimina prin calculul diferentelor
de ordinul I (cazul liniar) sau de ordin egal sau mai mare decat 2 (cazul
neliniar). Asadar, se recomanda ca stationarizarea seriei
cronologice sa fie realizata prin obtinerea de diferente in
lant astfel Yt=yt-yt-1=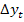
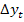
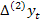
Pentru o departajare obiectiva, se recomanda testul DF (Dickey-Fuller). Verificarea semnalata prin initialelel DF presupune estimarea parametrilor functiei de regresie
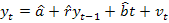
unde 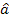
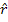
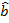
t=1, 2, 3, , n
vt=variabila reziduala stationara de medie egala cu zero si σ2 finita, diferita de zero.
Daca b=0 si 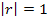
Daca b difera
semnificativ de zero iar 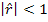
Copyright © 2025 - Toate drepturile rezervate