Dependente in economie manifestate in mod sincron sau cu decalaje in timp

DEPENDENTE IN ECONOMIE MANIFESTATE IN MOD SINCRON SAU CU DECALAJE IN TIMP

1. Seria integrata, serii co-integrate privind procese economice evolutive

Seria la care ne referim este, desigur, seria cronologica. Atributul "integrata" provine din englezescul "integrate" (a completa prin insumarea partilor). Caracterizarea seriei drept integrata poate fi inteleasa in sensul de redare a seriei prin parti (componente) care pot recompune seria originala prin insumare. Astfel, seria care urmeaza un trend liniar, prin calculul diferentelor de ordinul 1 (reprezentand elemente componente, parti) devine stationara. Este considerata o serie integrata de ordinul I ().

, (t=1,.,n-1) (1

Readucerea sirului termenilor la forma originala implica o insumare a componentelor in sensul ca

(2

Este posibil sa constatam si alte ordine de integrare decat 1:

Serie integrata de ordinul zero () - seria stationara;

Serie integrata de ordinul doi () - presupune ca sirul valorilor sa ajunga la starea de a fi stationar dupa transformari care implica determinarea diferentelor de ordinul 2 - , adica determinarea diferentelor succesive din diferentele anterior obtinute.

Concret, seriile pot prezenta evolutii care, din perspectiva conceptului de integrare, pot fi etichetate astfel:

Cazul 1

y: 2; 3; 2; 3; 2; 2; 3; 2; 3 intrucat este stationara este considerata integrata de ordinul zero - ;

Cazul 2

: 20; 22; 23; 25; 27; 27; 30; 32 intrucat prezinta tendinta care poate fi eliminata prin diferente de ordinul 1 (intr-adevar 23-22=1; 2; 2; 0; 3; 2) seria este considerata ca fiind integrata de ordinul 1 - ;

Cazul 3

: 8; 9; 12; 14; 16; 19; 25; 33; 43 - intrucat pentru a fi transformata in serie stationara este necesar sa calculam diferentele de ordinul 2, adica sa obtinem intr-o prima faza 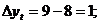12-9=3; 14-12=2; 2; 3; 6; 8; 10 iar in faza a 2-a diferente din diferente

iar in continuare rezulta 0; 1; 3; 2; 2, consideram seria ca fiind integrata de ordinul 2.

Serii co-integrate - sunt considerate acele serii cronologice care, pe langa faptul ca sunt serii integrate de acelasi ordin, admit o combinatie liniara care este integrata de ordin zero sau, in orice caz, este integrata de ordin mai mic decat ordinul de integrare al seriilor initiale.

Sa exemplificam astfel de serii:

: 1; 2; 3; 4; 5; 6 - intrucat 1; 1; 1; 1; 1

8; 10; 12; 14; 16; 18 - intrucat 2; 2; 2; 2; 2;

iar combinatia liniara 2*2+(1-2)*10=6; si in continuare -6; -6; -6 pentru care asa incat .

Rezulta ca seriile indeplinesc cele 2 conditii:

Ambele sunt integrate de acelasi ordin (ordinul 1);

Exista o combinatie liniara a seriilor care este o serie integrata de ordin zero, . Putem afirma ca seriile sunt co-integrate de ordin (1,0), notate

Abordarea unui numar de 2 sau mai multe serii cronologice din perspectiva ordinului de integrare al respectivelor serii, ca si a combinatiei liniare a acestora, formeaza obiectul asa-numitei analize de co-integrare.

Pentru a aprecia importanta unei astfel de analize avem in vedere si cuplul de serii care este "legat" printr-o relatie de tip cauza-efect, in sensul ca y=a+bx+u.

In situatiile in care atat sirul de valori cat si cel privind reprezinta, fiecare, un grad de integrare egal cu 1, iar combinatia liniara este integrata de ordin zero, afirmam ca seriile sunt co-integrate

Din perspectiva econometriei, astfel de serii conduc la o analiza de regresie de calitate in sensul ca estimatorii sunt consistenti (chiar supraconsistenti intrucat converg rapid spre valorile adevarate ale parametrilor) iar testele "t" si "F" sunt performante. Reversul: daca analiza de regresie este analizata pentru serii care nu sunt co-integrate (gradul de integrare pentru difera de cel obtinut pentru ) se ajunge la solitii fragile, indoielnice ("spurious regression") si ele ne sunt semnalate de autocorelarea variabilei reziduale (DW este apropiat de zero) in conditiile in care R, ca si rezultatele testului "t", satisfac.

Din perspectiva analizei statistice, dar si a celei economice, seriile cronologice co-integrate semnaleaza o stare de echilibru pe termen lung in ce priveste stilul de a evolua in timp. Astfel de serii par si deseori realmente tradeaza o relatie de influenta reciproca, asa incat in pofida unor vremelnice abateri in ce priveste coincidenta modificarilor in evolutie, ele "merg" impreuna.

Intuitiv, doua serii cronologice etichetate co-integrate trebuie percepute ca evoluand in acelasi ritm, fiind pe aceeasi lungime de unda, "prinse" intr-un dans in care pasii, desi nu-s identici, se conditioneaza reciproc.

In vederea aprecierii existentei co-integrarii dintre seriile de timp semnalam existenta mai multor teste specifice. Astfel, asa-numitul test CRDW (propus de Sargan si Bhargara) se bazeaza pe verificarea autocorelarii abaterilor (testul DW) si comparatia valorii calculate DW cu valorile tabelate de McKinnon (0,386 pentru a=0,05; 0,322 pentru a=0,10). Daca afirmam ca seriile sunt CI; in caz contrar (DW<0,386), seriile nu sunt CI. Testul DF este si el aplicabil si, in acest scop, pentru seriile se determina dupa care, pentru modelul autoregresiv, respectiv adica , (3

se estimeaza . Testul "t" aplicat estimatorului conduce la afirmarea co-integrarii, daca respectiv infirmarea CI pentru (unde prezinta valori specifice unei astfel de verificari).

2. Modele dinamice destinate includerii efectelor decalate in timp

Efectul celor mai multe dintre impulsurile date economiei prin intermediul factorilor exogeni se resimte dupa trecerea unui interval mai mic sau mai mare de timp.

Intre motivele care provoaca intarzieri in manifestarea actiunii unui factor deosebim:

Motive de natura psihologica, dintre care mentionam obiceiurile, inertia, teama. De exemplu, o crestere brusca a venitului nu determina o modificare totala a consumului datorita, pe de o parte, obisnuintelor si gusturilor incetatenite, iar pe de alta parte temerilor ca "aceasta nu va dura" (urmare a necunoasterii partiale a caracterului permanent sau tranzitoriu al modificarii cauzei);

Motivele de natura tehnologica, intre care cele privind adaptarea liniilor de fabricatie, a reconversiei fortei de munca, fac ca un impuls privind capitalul (de exemplu, ieftinirea utilajelor) sau mana de lucru (de exemplu, cresterea salariilor intr-un nou sector de activitate) sa produca un efect care doar dupa un timp se va manifesta pregnant;

Motive de ordin institutional - legate indeosebi de obligatiile contractuale (care conditioneaza aprovizionarea, livrarea, incasarea drepturilor, incasarea dobanzii pentru depozite la termen) care, de regula, au darul de a intarzia schimbarea in raport cu modificarea "peste noapte" a unor conditii.

Urmarea existentei in economie a unor astfel de motive face ca intarzierea raspunsului la unele masuri (impulsuri, modificari de politica economica) sa se manifeste de o asemenea maniera incat elasticitatea pe termen scurt devine irelevanta. Doar trecerea timpului si "dezlegarea" de obligatiile, obiceiurile si temerile care leaga comportamentul agentilor economici de trecut, fac ca rolul factorului sa apara tot mai relevant.

In raport cu durata de asteptare a efectului, intarzierile pot fi:

De durata scurta, de regula mai mica de 1 an (intensificarea reclamei, vanzarile; stimulentele materiale si productia; cresterea depunerilor si cresterea veniturilor din dobanzi; cresterea inflatiei si accelerarea circuitului banilor);

De durata medie, intre 1-3 ani (modernizarea tehnologiei si productia; modificari de legislatie si comportamentul economic; imbunatatirea calitatii produsului si cresterea vanzarilor, industrializarea si calitatea mediului etc.);

De lunga durata (investitiile in transporturi si rentabilizarea transporturilor precum si a altor activitati; dezvoltarea invatamantului si cresterea productivitatii si calitatii activitatilor etc.).

Pentru a evidentia efectul aparut cu intarziere de 1,2,., perioade, folosim termenul "lag", iar reprezentarile care includ factori cu efect intarziat sunt considerate modele lag sau modele dinamice.

Problemele de masurare care apar in specificarea si utilizarea modelului lag in analiza si prognoza economica sunt: a) stabilirea unitatii de timp la care se refera fiecare nivel al variabilelor modelului; b) delimitarea intarzierii aparitiei efectului in urma modificarii cauzei; c) estimarea parametrilor.

a)      Stabilirea unitatii de timp careia ii corespunde un nivel presupune alegerea intre posibilitatile de a obtine date anuale, trimestriale, lunare, saptamanale, eventual cincinale sau decenale. O unitate de timp prea mare face inaccesibila depistarea de influente cu intarzieri de durate scurte; alegerea unei unitati de timp prea mici poate provoca dificultati in ce priveste obtinerea datelor sau delimitarea intarzierilor de durata lunga. Ca urmare, ne bazam in optiunile noastre pe particularitatile fenomenului, obiectivele demersului econometric si, nu in ultimul rand, pe posibilitatile existente de a obtine date privind unitatea de timp considerata revelatoare. Referitor la acest din urma aspect, mentionam ca deseori datele sunt anuale, caz in care posibilitatile de alegere sunt aproape nule.

b)      Delimitarea intarzierilor la care efectul raspunde atunci cand variabila exogena se modifica poate beneficia de avantajele unei reprezentari grafice adecvate acestui scop. Astfel, cronograma privind evolutia variabilei cauzale, expusa pe o hartie de calc si suprapusa cronogramei variabilei efect, poate pune i evidenta (printr-o simpla deplasare a uneia dintre cronograme pe axa timpului) o analogie care apare dupa una sau mai multe unitati de timp.

Un procedeu bazat indeosebi pe sensibilizarea coeficientului de determinatie (varianta ajustata) de catre introducerea unui "factor" suplimentar in sensul de crestere cu inca o perioada a intarzierii de la care se simte efectul, presupune parcurgerea urmatoarelor etape:

Prestabilirea unui interval rezonabil ca marime dupa trecerea caruia se poate accepta ca factorul nu mai poate exercita practic nicio influenta notabila asupra variabilei efect. De exemplu, venitul realizat in trecut, in urma cu mai mult de 7 luni, nu mai determina cuantumul economiilor din luna prezenta. Asadar, acceptam ca modificarile de venit de acum o luna, 2 luni, 3 luni etc. influenteaza marimea economiilor depuse la banca de catre membrii unei familii, dar ceea ce s-a castigat acum 8 luni, practic nu mai exercita nicio influenta;

Procedam la estimarea parametrilor, urmata de calculul coeficientului (vezi relatia 4.11) pentru cele 7 ecuatii elaborate in succesiune astfel

, corespunzator calculam (4

, precum si (5

, precum si (6

In final se constata pentru care dintre ecuatii s-a obtinut cel mai mare nivel al coeficientului (ceea ce corespunde variantei cu cea mai mica dispersie a valorilor reziduale) si aceasta ecuatie va fi retinuta in vederea analizei si prognozei.

c)      In ceea ce priveste parametrii modelelor cu efect intarziat (modele lag, modele dinamice), acestia sunt variabili ca numar in raport cu tipul de model rezultat in urma specificarii). In mod frecvent deosebim:

Modele unifactoriale in care efectul se resimte dupa o intarziere de o unitate de timp.

(7

(unde y se poate referi la: productivitate, oferta, recolta; corespunzator, x poate reprezenta: - utilajele, cererea, umiditatea solului).

Modele autoregresive in care intarzierea este distribuita (esalonata) pe mai multe unitati de timp

(8

(unde y - consumul sau acumularile sau profitul.)

Modele mixte in care variabilele cauzale, cu sau fara efect intarziat, pot fi de natura exogena (x) sau autocorelate ()

(9

(unde y poate fi cererea sau calitatea, corespunzator x poate fi venitul sau utilarea)

modele in care variabila factoriala (x) isi transmite efectul in mod treptat atat in perioada t cat si pe parcursul unui numar finit de perioade de intarziere. Asadar, este presupusa o distributie a influentei pe mai multe perioade de timp (lag distribuit sau intarzieri esalonate)

(10

(unde: y - productia, x - investitiile; y - inflatia, x - cresterea ofertei de bani; y - marimea depozitului, x - dobanda cu capitalizare).

Intr-un astfel de model, parametrului ii putem atribui semnificatia economica de multiplicator de impact intrucat exprima modificarea in medie a variabilei y la o modificare unitara a variabilei x in aceeasi perioada "t". prezinta interes semnificatia sumei () daca modificarea variabilei x se mentine si in perioada urmatoare, respectiv sumei () in perioada viitoare etc. Astfel de sume partiale reprezinta multiplicatori interimari, in timp ce suma reprezinta in (10) multiplicatorul total pe termen lung

Intre variantele modelului cu lag distribuit se detaseaza, prin frecventa aparitiei lor in studiile aplicative, urmatoarele doua reprezentari:

a). varianta descresterii in timp a efectului generat de modificarea factorului

(11

unde k=constanta subunitara

b). varianta cresterii treptate a efectului urmata de o descrestere treptata pana la anulare

(12

() (13

Inainte de a aborda mai in detaliu modelele specifice fiecarei variante, mentionam ca, in principiu, metoda celor mai mici patrate poate fi utilizata in vederea estimarii, in diverse variante. O prima varianta s-ar datora lui Alt si Tinbergen, care au propus ca in cazul modelului cu lag distribuit (10) sa se procedeze secvential astfel: intr-o prima etapa sa se estimeze parametrii modelului ; in cea de-a doua estimare sa se refere la , urmand apoi si asa mai departe, pana cand marimea nesemnificativa a ultimului parametru sau schimbarea semnului acestuia (in raport cu estimatiile anterioare) semnaleaza ca este irelevanta indepartarea in trecut. In acest fel, pe langa estimare s-ar rezolva si problema stabilirii obiective a ordinului (marimii lag-ului) modelului cu efecte intarziate. Motive precum multicoliniaritatea dintre etc. si efectul ei "distructiv" asupra estimatiilor, ca si dimensiunea relativ redusa a seriilor de timp de care, de regula, dispunem, au facut ca procedeul sa fie rareori utilizat.

Estimarea folosind MCMMP in cazul reprezentarilor (8-10 si 12) conduce la parametrii care nu sunt eficienti si nici suficient de stabili datorita dependentei variabilei cauzale de perturbatie, ca si datorita coliniaritatii. Astfel, reprezentarea autoregresiva 8 include intre factori pe care depinde de (daca depinde de nici nu face exceptie); varianta distribuirii influentei factorului x (10, 12) include factorii care, foarte probabil, sunt intens corelati (analogiile in evolutie fiind semnificative). Ambele reprezinta neconfirmari ale unor ipoteze ale modelului liniar si metodei de estimare (vezi cap. 5 si 6) cu repercursiuni negative asupra rezultatelor estimarii. In plus, apare si o problema datorata numarului mare de parametrii.

In scopul evitarii acestor surse de deformare a parametrilor estimati, se recomanda:

realizarea unor transformari in vederea reducerii numarului acestora, indeosebi in modelele cu lag distribuit (10). astfel, transformarea Koyck presupune ca in cazul modelului 10 sa realizam o decalare cu o unitate de timp (deci devine devine ), sa inmultim aceasta noua ecuatie cu o constanta "k" ceea ce rezulta, sa scadem din ecuatia initiala (10). obtinem in urma simplificarilor succesive:

(14

In ecuatia la care s-a ajuns (14), fenomenul multicoliniaritatii este diminuat intr-o foarte mare masura, ceea ce nu se poate afirma si cu privire la independenta variabilei explicative fata de perturbatia (v).

Modelul cu lag distribuit care presupune transformarea Koyck desi este considerat restrictiv, chiar rigid in ce priveste modul de abordare a influentei intarziate [30] este util in situatii in care rolul influentei intarziate scade rapid.

O alta modalitate de transformare este intalnita in cazul /12) si este cunoscuta sub denumirea de modelul ALMON. Acesta, prin comparatie, pare mai flexibil considerand influenta repartizata in timp ca fiind bine descrisa de un polinom de gradul 2, care pe masura ce inaintam in timp atinge un maxim, apoi intensitatea efectelor scade. Nu este exclusa nici posibilitatea ca boltirea curbei sa fie inversa si nici situatia in care un polinom de gradul 3 sau mai mare descrie mai bine evolutia intensitatii influentei intarziate. Shirley Almon considera, bazandu-se pe teorema lui Weierstass, ca parametrii modelului cu lag distribuit pot fi aproximati printr-un polinom de gradul i corespunzator lungimii intarzierii (lag-ului).

Astfel, pentru cazul in care intensitatea influentei urmeaza, in timp, o functie reprezentata de un polinom de gradul 2 avem in vedere expresia

(15

respectiv, pentru cazul general expresia

(16

(m<lungimea maxima a lag-ului).

Etapele premergatoare aplicarii propriu-zise a procedeului propus de Almon se refera la:

a). stabilirea numarului maxim de perioade in care influenta intarziata este semnificativa, avandu-se in vedere faptul ca un numar prea mare (k>5) poate creste considerabil riscul de a include influente irelevante, cu efecte nedorite asupra preciziei estimatorilor, in timp ce un numar prea mic risca sa "scoata din joc" efecte intarziate semnificative (determinante) asupra variabilei y. analiza semnificatiei parametrilor (in sensul testului "t") ar putea fi utila in stabilirea marimii lag-ului;

b). stabilirea gradului polinomului (m) utilizat pentru a descrie evolutia parametrilor in raport cu intarzierea. In functie de numarul punctelor de turnura este stabilit si gradul polinomului. De exemplu, daca pe masura de intervalul dintre declansarea cauzei si producerea efectului creste, influenta incepe prin a creste, atinge un maxim, dupa care descreste - se apreciaza existenta unui singur punct de turnura (schimbare de sens), asa incat un polinom de gradul 2 este considerat adecvat. Intrucat si in cazul modelului Almon exista pericolul ca multicoliniaritatea sa afecteze rezultatele, se recomanda ca numarul regresorilor () sa fie cat mai mic.

Aceste aspecte odata rezolvate, se poate trece la estimarea parametrilor. In acest scop, avem in vedere o evolutie a intensitatii influentei intarziate corespunzatoare polinomului de gradul 2, frecvent utilizat in aplicatii concrete () in cazul unui model cu lag distribuit pentru 3 perioade de intarziere

Daca avem in vedere relatia (15) si o introducem in (17) obtinem

In continuare, definim variabilele astfel:

; ; (19

asa incat putem reformula modelul (11) astfel:

(20

Estimatorii sunt obtinuti prin MCMMP.

Parametrii modelului initial (17) sunt estimati, urmand procedeul rezultat din teorema lui Weierstass, astfel:

,

(21

In ce priveste acuratetea estimatiilor astfel obtinute, mentionam ca multicoliniaritatea continua sa reprezinte o "problema" (aceasta si pentru faptul ca variabila Z reprezinta o combinatie liniara a variabilelor X care sunt, frecvent, coliniare). La acestea se mai adauga unele limite datorate subiectivismului (total sau partial) care intervine in optiunea privind gradul polinomului si marirea lag-ului. Totusi modelul Almon prezinta si o serie de avantaje, fiind mai flexibil in sensul ca face posibila alegerea intre diverse tipuri de influente intarziate (descrise printr-un grad adecvat al polinomului) la care se adauga faptul ca variabila nu apare in postura de regresor, eliminandu-se astfel si riscul corelarii unui factor () cu perturbatia (risc existent in cazul optiunii pentru varianta care implica transformata Koyck).

Exemplificarea care urmeaza se refera la datele statistice lunare privind evolutia taxei scontului () si a ratei medii a dobanzilor bancare active () in intervalul 1994 incepand cu luna a VI-a - 1999 pana in luna martie:

Acceptandu-se ipoteza (propusa de teoria economica) conform careia modificarea taxei scontului influenteaza rata dobanzii in perioada respectiva dar si in perioadele imediat urmatoare, a fost adoptat modelul cu lag distribuit . S-a considerat ca suntem in prezenta unui lag distribuit geometric si, ca urmare, s-a apelat la transformarea Koyck. In urma estimarii parametrilor s-a obtinut .

O modalitate de a analiza seriile de timp are in vedere urmatoarea tipologie: serii precursoare (lideri), serii sincrone, serii "intarziate".

Modelele lag permit analiza semnalelor VARIABILELOR PRECURSOARE si obtinerea de previziuni bazate pe evolutia acestora. Studiul evolutiei variabilelor precursoare (lideri) a caror calitate de a semnala aparitia unor efecte economice nedorite (epuizarea resurselor, inflatia, saturarea pietei etc.) le face deosebit de utile analizei si prognozei. Cunoasterea unor astfel de variabile, masurarea intarzierii si intensitatii efectului lor, atunci cand ele pot determina variabila-efect, poate fi abordata prin modele de tipul celor prezentate (7 - 10).

Redam mai jos exemple de variabile lideri prezentate in paralel cu variabile a caror evolutie succede liderilor intr-un mod asemanator dupa trecerea unui interval mai mic sau mai mare de timp.

Modele VAR (Vectorial autoregresive)

Intre variabilele modelului LAG am intalnit reprezentarea de tip autoregresiv, in sensul ca variabila-efect era considerata dependenta de propriile niveluri realizate in trecut si de perturbatia "actuala". Asadar,

(22

in cazurile in care extindem aceasta modalitate de exprimare asupra mai multor variabile-efect, dependente de "propriul lor trecut", ne aflam, cel putin sub aspectul reprezentarii formale, in prezenta unui VECTOR al VARIABILELOR-EFECT exprimat in raport cu performantele anterioare ale componentelor acestuia. In scrierea matriceala, pentru cazul a 2 variabile (Y1, Y2) modelul VAR poate fi redat astfel:

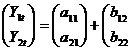
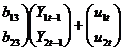(23

intr-o formula concentrata

Y - vectorul variabilelor-efect; A - vectorul parametrilor liberi; B - matricea patrata a parametrilor; - vectorul variabilelor-efect decalate cu 1; V - vectorul perturbatiilor.

Un astfel de model (23) este considerat de ordinul 1 intrucat marimea maxima a lag-ului este de unu; un model de ordin k, elaborat pentru m variabile-efect poate fi reprezentat astfel:

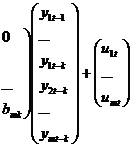(24

Reprezentarea intalnita sub denumirea de modelul VAR indeosebi pentru a descrie interdependenta dintre variabilele-efect. O astfel de interdependenta este redata printr-un ansamblu de ecuatii de regresie de forma:

(25

sistemul astfel reprezentat descrie relatia dinamica dintre doua variabile endogene ale modelului: Consumul, Veniturile.

Intr-un viitor capitol astfel de reprezentari sunt denumite modelele cu ecuatii simultane. Aspectul autoregresiv intr-un astfel de model apare pe ansamblu, in sensul ca variabilele-efect ale modelului (consumul, venitul) depind de valorile anterioare inregistrate de aceleasi variabile (consum si venit). Constatarea este si mai bine pusa in evidenta daca procedam la inlocuirea variabilei Venit din prima ecuatie (in care apare ca factor) cu expresia sa (cea de a 2-a ecuatie a modelului (25):

(26

Daca notam ecuatia 26, la care adaugam ecuatia venitului, conduce la sistemul

(27

In capitolul destinat prezentarii modelelor cu ecuatii simultane (cap. XII) o astfel de redare a modelului este denumita forma redusa. Pentru obtinerea de prognoze si simulari este forma cea mai convenabila. Si in acest caz ordinul modelului VAR este dat de marimea maxima a lag-ului evidentiat in cazul uneia sau a tuturor variabilelor cu efect intarziat (aflate in dreapta semnelor de egalitate). Estimarea parametrilor presupune aplicarea MCMMP fiecarei ecuatii din asa-numita forma redusa (27) a modelului autoregresiv.

Recomandari in ce priveste specificarea si utilizarea modelului VAR:

tendinta, ca si sezonalitatea, daca exista, sunt in prealabil eliminate din date atunci cand utilizam serii cronologice;

media valorilor reziduale () este zero iar autocorelarea erorilor este exclusa din modelul (27);

imprastierea valorilor reziduale este constanta.

Aceste conditii fiind indeplinite, estimarile pentru 27 sunt consistente si asimptotic normal distribuite, oferind o baza solida testarii dar si prognozelor bazate pe astfel de modele. Limitele modelelor VAR: baza teoretica (avem in vedere teoria economica) este fragila; lungimea ag-ului poate fi partial subiectiva, interpretarea estimatiilor din perspectiva economiei este discutabila.