Intervalele simple si denumirea lor

Se numesc intervale simple toate acele intervale care se formeaza in spatiul unei octave.

Dupa numarul treptelor ce cuprind din scara sonora octavianta, ele poarta urmatoarele denumiri: ³

- prima (in limba latina primus-a-um) repetarea sunetului de pe aceeasi treapta a scarii:[1]

- secunda (secundus-a-um) intervalul format intre o treapta data si a doua din ordinea succesiva a scarii:

- terta (tertius-a-um) = intervalul format intre o treapta data si a treia din ordinea succesiva a scarii:

- cvarta (quartus-a-um) = intervalul format intre o treapta data si a patra din ordinea succesiva a scarii:

- cvinta (quintus-a-um) = intervalul format intre o treapta data si a cincea in ordinea succesiva a scarii:

- sexta (sextus-a-um) = intervalul format intre o treapta data si a sasea din ordinea succesiva a scarii:

- septima (septimus-a-um) = intervalul format intre o treapta data si a saptea din ordinea succesiva a scarii:

- octava (octavus-a-um) = intervalul format intre o treapta data si a opta din ordinea succesiva a scarii:

Determinarea acustico - matematica a intervalelor

a) Primul procedeu de exprimare a unui interval pe cale acustico-matematica foloseste o relatie cifrica in care numaratorul reprezinta frecventa sunetului inalt (varful intervalului), iar numaratorul frecventa sunetului grav (baza intervalului). De exemplu: octava do² - do¹ = 528/265; cvinta sol¹ - do = 396/264; sexta la^l - do^l = 440/264 etc.

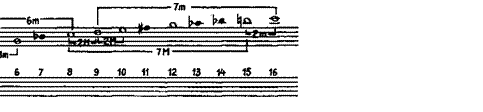b) Al doilea procedeu de exprimare a unui interval pe cale acustico-matematica utilizeaza pozitia sunetelor ce compun intervalul respectiv in seria armonicelor. Fie, spre exemplu, armonicele sunetului fundamental do, in care vom indica intervalele muzicale mai uzuale ce apar intre primele 16 armonice:

Tinand seama de armonicele intre care se formeaza, fiecare interval poate fi exprimat printr-o relatie a doua cifre reprezentand: una (numaratorul) ar­monicul superior, iar cealalta (numitorul) armonicul inferior. De exemplu (se dau numai intervalele uzuale):

Octava perfecta: 2/1 = intervalul dintre armonicele 1, 2;

Cvinta perfecta: 3/2 = intervalul dintre armonicele 2, 3;
- Cvarta perfecta: 4/3 = intervalul dintre armonicele 3, 4;

Terta mare: 5/4  = intervalul dintre armonicele 4, 5;

Terta mica: 6/5 = intervalul dintre armonicele 5, 6;

Secunda mare: 9/8 = intervalul dintre armonicele 8, 9

si 10/9 (tonul mare) si 9, 10 (tonul mic);

- Secunda mica: 16/15 = intervalul dintre armonicele 15, 16;

Sexta mare: 5/3  = intervalul dintre armonicele 3, 5;

Sexta mica: 8/5  = intervalul dintre armonicele 5, 8;

- Septima mare: 15/8  = intervalul dintre armonicele 8, 15;

Septima mica: 9/5  = intervalul dintre armonicele 5, 9.

Toate intervalele exprimate prin relatii acustico-matematice descrise mai sus se numesc naturale, dimensiunile lor rezultand fie din redarea frecventelor sunetelor componente (deci inaltimea absoluta), fie din pozitia armonicelor intre care se formeaza.

Cunoscand modalitatea de determinare acustico-matematica a intervalelor, putem efectua operatiuni deosebit de utile privind raporturile naturale (fi­zice) dintre diferitele sunete.

Astfel, pentru aflarea frecventei unui sunet mai acut, se inmulteste frecventa sunetului de la care se porneste cu fractia care reprezinta intervalul despartitor, ca in exemplul urmator: do¹ x 5/3 (sexta mare) = la adica 264 x 5/3 = 440Hz.

Daca, dimpotriva, dorim sa aflam frecventa unui sunet mai grav decat cel de la care pornim, se procedeaza invers, prin impartirea cu fractia ce reprezinta intervalul despartitor: la¹ : 5/3 (sexta mare) do adica. 440 : 5/3 = 264 Hz.

În lumina creatiei contemporane, asemenea calcule matematice, care mai inainte constituiau apanajul strict al omului de stiinta, trebuie sa devina tot atat de familiare si omului de arta.