INCOVOIEREA PURA , FORMULA LUI NAVIER

INCOVOIEREA PURA , FORMULA LUI NAVIER

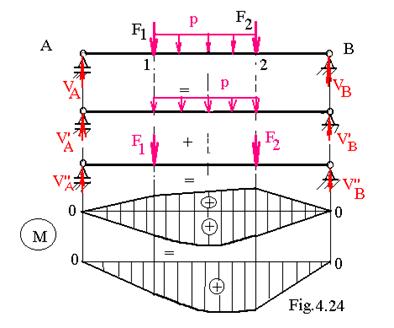
Asa cum s-a definit anterior , incovoierea pura este incovoierea fara forta taietoare , sau in centrul de greutate al sectiunii transversale a barei apare doar momentul incovoietor , dirijat dupa una din axele principale de inertie Oz sau Oy . Pentru a stabili care este relatia dintre momentul incovoietor si efortul unitar este necesar sa se cunoasca modul de distributie al efortului unitar in sectiune .

a)   Studiu geometric

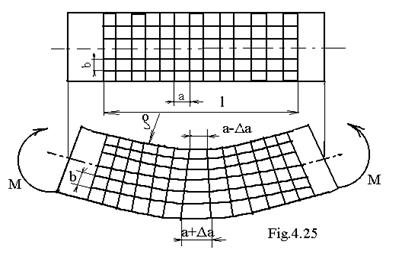
Pe suprafata exterioara a unei bare de sectiune dreptunghiulara , se traseaza o retea de reperi transversali paraleli echidistanti ce materializeaza sectiunile transversale si o retea de reprei longitudinali de asemenea echidistanti ce materializeaza sectiunile longitudinale ( fig. 4. 25 )

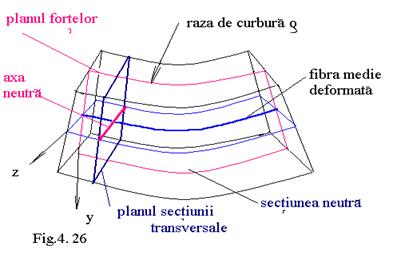
Bara este supusa unui moment incovoietor pozitiv . Sub actiunea acestui moment, axa barei devine curba , reperii longitudinali se curbeaza cu raza de curbura r, cei de la partea superioara se scutreaza iar cei de la partea inferioara se lungesc . Deci exista o fibra a carei lungime ramane constanta, si se numeste fibra medie deformata . Totalitatea fibrelor care raman de lungime constanta formeaza o suprafata numita suprafata neutra ( fig. 4.26 )

Reperii transversali se rotesc , ramanand plani si perpendiculari pe axa barei ceea ce confirma aplicabilitatea ipotezei lui Bernoulli .

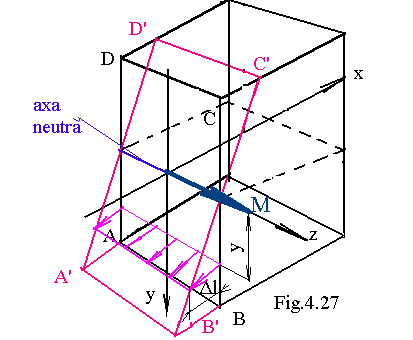
Intersectia dintre planul sectiunii transversale si suprafata neutra se face dupa axa neutra (fig.4.27).

Intersectia dintre suprafata neutra si planul fortelor se face dupa fibra medie deformata .

Sectiunea ABCD se roteste in jurul axei neutre ajungand in pozitia A'B'C'D' , ramanand plana ( fig. 4 .27 ).

Lungirea unei fibre situate la distanta y de axa neutra se va nota ∆ l _y si este proportionala cu departarea y fata de axa neutra :

( 4 . 46 )

Alungirea corespunzatoare va fi :

( 4 . 47 )

Dar :

( 4 . 48 )

Tinand cont de relatiile ( 4 . 47 ) si ( 4 . 48 ) se poate scrie :

( 4 . 49 )

Tinand seama de legea lui Hooke si de relatia ( 4 . 49 )se obtine :

( 4 . 50 )

b)   Studiu static

relatie ce determina legea de variatie a tensiunilor normale pe sectiunea transversala , adica , tensiunea normala variaza liniar cu departarea fata de axa neutra .

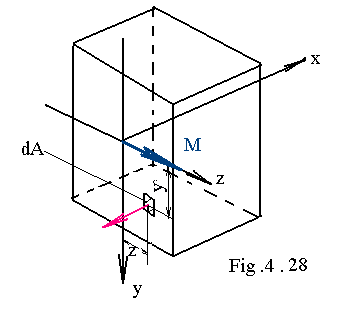
Fie un element de arie da de pe suprafata ABCD a sectiunii transversale ( fig.4 . 28), situat la distanta y fata de axa neutra .Pentru acest element pot fi scrise ecuatiile de echilibru static :

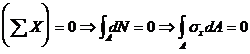( 4 . 51 )

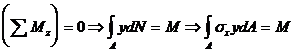( 4 . 52)

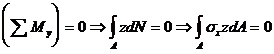( 4 . 53 )

c) Studiu fizic

Tinand cont de legea lui Hooke , inlocuind pe σ_x cu relatia ( 4 . 50 ) se vor obtine :

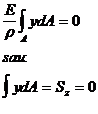( 4 . 54 )

In care S_z se numeste moment de inertie static al sectiunii transversale in raport cu axa neutra . Deoarece el are valoare nula , inseamna ca , axa neutra trece prin centrul de greutate al sectiunii transversale .

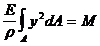( 4 . 55 )

In relatia ( 4 . 52 ) :

    ( 4 . 56 )

reprezinta momentul de inertie geometric axial in raport cu axa Oz .Tinand seama de relatia (4 . 56 ) se poate scrie :

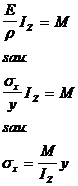( 4 . 57 )

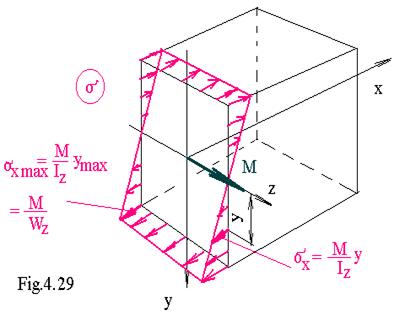
ceea ce reprezinta variatia tensiunii normale pe sectiunea transversala , sau formula lui Navier.Conform acestei relatii , tensiunile variaza liniar cu departarea fata de axa neutra , crescand o data cu aceasta , deci sunt maxime pentru cele mai indepartate fibre ale sectiunii transversale ( fig. 4. 29).

Inlocuind si in cea de a treia relatie valoarea tensiunilor normale :

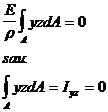( 4 . 58 )

se obtine I_yz momentul de inertie centrifugal al sectiunii transversale , a carei valoare se anuleaza , ceea ce duce la concluzia ca : axele Oy si Oz sunt axe principale de inertie ale sectiunii transversale .

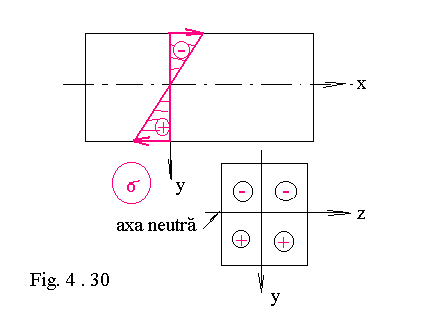
Din relatia lui Navier se obtine valoarea tensiunii maxime in cea mai indepartata fibra fata de axa neutra . Deci :

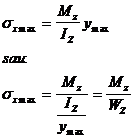( 4 . 59 )

In care:

( 4 . 60 )

se numeste modul de rezistenta la incovoiere , si reprezinta un element geometric ce caracterizeaza sectiunea transversala .

Uneori se poate renunta la indicele z .Variatia tensiunii normale in sectiunea transversala este prezentata in figura 4. 29 si 4.30 .

1.Calculul de rezistenta la incovoiere pura

a)   Dimensionare

Pentru a dimensiona un element de rezistenta se va scrie formula lui Navier sub forma :

( 4 . 61 )

iar pentru a stabili care sunt dimensiunile sectiunii transversale se vor stabili care sunt modulele de rezistenta pentru cateva sectiuni transversale uzuale :

Pentru sectiunea circulara de diametru D :

n    fibra cea mai departata de axa neutra se afla la distanta y_max =D/2

n    Deci :

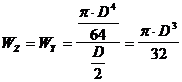( 4 .62 )

Pentru sectiunea inelara de diametre D la exterior si d la interior:

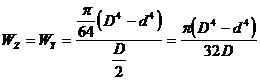( 4 . 63 )

Evident ca pentru a putea dimensiona o sectiune inelara trebuie sa se cunoasca o relatie intre cele doua diametre , sau chiar unul dintre ele .

Pentru sectiunea dreptunghiulara de dimensiuni b si h

n    fibra cea mai indepartata fata de axa neutra se afla la distanta y_max =h/2

Deci :

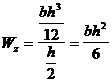( 4 .64 )

sau daca distanta maxima este y_max =b/2

( 4 . 65 )

Comportarea cea mai buna la incovoiere o au profilele laminate , a caror module de rezistenta la incovoiere si momente de inertie axiale se gasesc in tabele in functie de tipul standard al profilului .

Observatie :

In calculele de dimensionare trebuie sa se tina seama atat de conditiile de rezistenta cat si de cele economice .Elementele de rezistenta trebuie astfel confectionate sa reziste solicitarilor , dar sa aibe un consum redus de material , respectiv modulul de rezistenta mare , greutatea ( sau aria sectiunii ) mici . Criteriul de economicitate se exprima prin raportul W/A. Astfel , pentru sectiunea circulara :

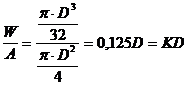( 4 . 66 )

-pentru sectiune dreptunghiulara :

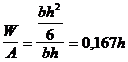( 4 . 67 )

Cu cat k este mai mare , la aceeasi arie si consum de material modulul de rezistenta este mai mare , deci piesa mai rezistenta la incovoiere .

In cazul profilelor laminate , valoarea coeficientului k este cuprinsa intre 0,28 si 0,32 , adica la aceasi arie un profil laminat standard este de trei ori mai rezistent la incovoiere fata de sectiunea circulara ( la aceeasi arie , pentru cerc , y_max este mai mic sectiunea fiind adunata in jurul centrului de greutate , in timp ce la un profil I de exemplu , y_max este mai mare , sectiunea fiind departata fata de axa neutra )

b)   Verificare :

Pentru a verifica daca un element de rezistenta rezista la incovoiere , din conditia de rezistenta , relatia lui Navier se scrie :

(4. 68 )

in care sigur ca verificarea se va face pentru cea mai mare valoare a momentului incovoietor M_max ( valoare ce trebuie determinata din diagrama de moment incovoietor ).

c)   Calculul momentului capabil

( 4 . 69 )

reprezinta valoarea momentului incovoietor la care rezista un element de rezistenta a carei sectiune transversala are modulul de rezistenta W_ef , confectionat dintr-un material pentru care se cunoaste σ_a .