 | Aeronautica | Comunicatii | Constructii | Electronica | Navigatie | Pompieri |
| Tehnica mecanica |
Semnale modulate
1.Scopul lucrarii
Analiza spectrala a oscilatiilor modulate in amplitudine (MA) si in frecventa (MF),cu semnal modulator sinusoidal.
2.Notiuni teoretice
In general,un semnal modulat,cu purtatoare sinusoidala are forma:
![]()
unde:
A(t)=amplitudinea oscilatiilor;
t)=unghiul de faza;
Frecventa instantanee este ![]()
Sa presupunem ca plecam de la semnalul purtator:
![]()
Se noteaza semnalul modulator astfel:
![]()
Utilitatea imediata a modulatiei o
reprezinta transpunerea unui semnal din joasa frecventa in inalta frecventa,ceea ce duce la o mai buna protectie a semnalului impotriva
zgomotului.De aceea,![]()
Parametrul semnalului care este supus variatiei modulatorului este la semnalul modulat in amplitudine,chiar amplitudinea sa care variaza astfel in timp,variatie data de xm(t):
![]()
Atunci,semnalul modulat are forma:
![]()
kA este o

Prin urmare,spectrul de amplitudine contine trei componente:
-purtatoarea,de amplitudine U0;
-doua componente laterale (superioara,inferioara) de amplitudine ![]() ,aflate la frecventele
,aflate la frecventele ![]()
Amplitudinea oscilatiei variaza
intre valorile ![]() . Atunci se poate deduce
urmatoarea expresie pentru gradul de modulatie:
. Atunci se poate deduce
urmatoarea expresie pentru gradul de modulatie:
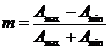
La semnalul modulat in frecventa,frecventa prezinta in timp o variatie data de semnalul modulator:
![]()
Se folosesc notatiile:
![]()
Atunci,vom putea scrie forma finala a semnalului modulat in frecventa sub forma:
![]()
in care 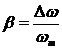 reprezinta indicele
de modulatie.
reprezinta indicele
de modulatie.
Acest semnal poate fi descompuns intr-o serie de functii ortogonale,numite functii Bessel de prima speta,de indice n si argument ,asa cum se arata mai jos:
![]()
Deci,semnalul are urmatoarele componente:
-o purtatoare de amplitudine
![]()
-o infinitate de componente laterale inferioare si superioare de
amplitudine ![]() cu frecventele
cu frecventele ![]()
Desi nu descresc uniform,componentele incep sa descreasca uniform atunci cand n> si putem neglija componentele de indici foarte mari in modul.De asemenea,componentele nu descresc simetric.Pentru anumite valori ale lui ,purtatoarea se anuleaza.
3.Desfasurarea lucrarii
Se vor folosi:
Un generator de functii GF,cu posibilitatea de modulare in amplitudine si frecventa,cu un semnal modulator extern aplicat la bornele MA,respectiv MF.Se lucreaza cu f0=500kHz.
Un generator de joasa frecventa GFJ,care furnizeaza o tensiune modulatoare de amplitudine Um si frecventa fm (fixata la 5kHz).
MVS,un milivoltmetru selectiv.
MV,un milivoltmetru pentru masurarea tensiunii Um.
OSC,un osciloscop pentru vizualizarea semnalului modulat.
A.Semnalele MA
Se va masura fradul de modulatie al unui semnal MA.Se va folosi formula:
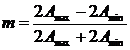
Cu ajutorul milivoltmetrului selectiv,se folosesc MV,FVS pe frecventa de 500kHz.Se masoara componentele spectrale prin nivelul lor in dB si se transforma in [V] alegand o tensiune de referinta de 0.775V, dupa formula:
![]()
In tabelul 1 din anexa s-au reprezentat valorile masurate si prelucrarile aferente,iar gradul de modulatie se poate reprezenta prin dependenta sa de Um,rezultand o dreapta caracterizata de trei puncte:
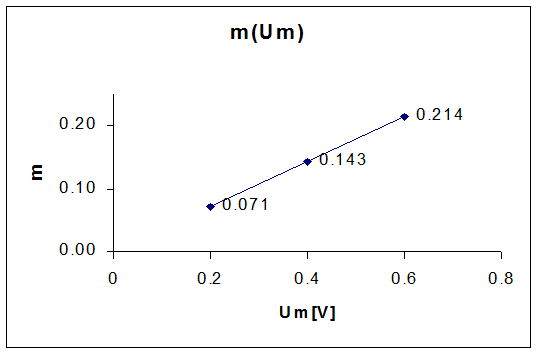
Din acest grafic,putem deduce coeficientul caracteristic al modulatorului kA,ca fiind panta dreptei reprezentate mai sus.
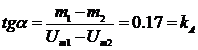
B.Masuratori asupra semnalelor MF
Se seteaza din nou frecventa semnalului purtator la 500kHz.Se foloseste metoda extinctiilor purtatoarei.Am vazut ca J0 se poate anula pentru o anume valoare a argumentului.Se gaseste purtatoarea cu ajutorul MV si se anuleaza Um,facandu-se nivelul purtatoarei 0dB.Se cauta apoi un minim al purtatoarei.Se mareste in continuare Um pentru urmatoarele 4-5 extinctii.Se reprezinta f(Um),pe baza tabelului 2:
Vom masura acum spectrele unor semnale MF,alegand o banda de frecventa anume si lucrand la f mici,acolo unde dependenta din graficul de mai sus poate fi aproximata ca fiind liniara.
Se fac masuratori pentru doua benzi de frecventa diferite,datele fiind reprezentate in tabelul 3.
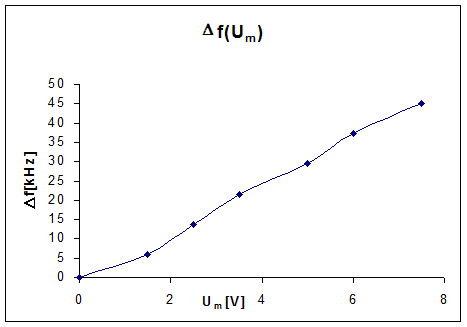
De exemplu,pentru f=5kHz,spectrul arata astfel:
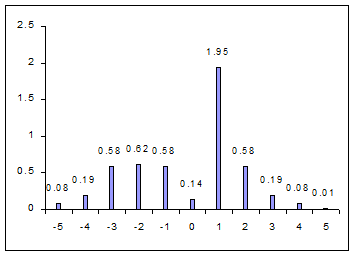
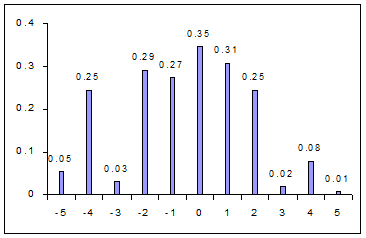
Iar,pentru f=15kHz,spectrul arata astfel (conform tabelului 4):
Observatie
Atunci cand banda se largeste,amplitudinile armonicelor se micsoreaza.
4.Intrebari si raspunsuri
1.Cum trebuie sa arate caracteristica ideala m(Um) si ce semnificatie are abaterea de la forma ideala?
Caracteristica trebuie sa fie liniara,dar exista abateri de la aceasta caracteristica prin erorile de masura.Totusi,in lucrare,dependenta este liniara,cele trei puncte care determina graficul,fiind aproape coliniare.
2.Ce caracteristici ale osciloscopului pot influenta precizia masuratorii gradului de modulatie?Calibrarea treptelor de amplitudine are vreun efect?
Pentru calculul gradului de modulatie,se fixeaza pe ecranul osciloscopului 30 de diviziuni.Aceasta fixare poate provoca erori de citire, deoarece diviziunile nu pot incapea de un numar intreg de ori in amplitudinea semnalului.
3.Evaluati largimea de banda ocupata de spectrele MF masurate pentru =0.01.Sa
se compare cu relatia ![]()
Pentru f=5kHz,daca incercam sa detectam erorile aparute de-a lungul masuratorilor,banda este de 6kHz. Dupa formula, considerand =2 va rezulta o banda de aproape 20kHz.Acest lucru nu trebuie interpretat ca o eroare a masuratorilor,din moment ce am masurat nivelurile doar pentru intervalul -5..5.Pentru f=15kHz,banda este de aproximativ 6kHz.Cu formula,rezulta o banda mai mare de 75kHz.
4.Cum se modifica largimea benzii ocupata de spectrul MF daca se mentine Um constant si se variaza fm?
Daca se mentine Um constant si se
variaza fm,inseamna ca se mentine 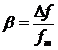 variaza invers proportional cu fm.
variaza invers proportional cu fm.
![]()
In formula de mai sus,doar primii doi termeni sunt variabili, variind datorita lui fm in aceeasi directie,ultimul termen fiind constant datorita ipotezei.Prin urmare,largimea de banda variaza in acelasi sens cu frecventa modulatoare.
5.Cum se poate recunoaste cu ajutorul analizei spectrale ca un generator MA produce si o oscilatie MF parazita?
Desi in urma unor MA,MF luate individual,spectrul de amplitudini este simetric fata de purtatoare,atunci cand aceste modulatii se produc simultan,spectrul nu mai este simetric fata de purtatoare.Aceasta este o metoda de a verifica eventuala aparitie a unei MF parazite:simetria spectrului.
6.Prin ce procedee se poate pune in evidenta ca un generator MF produce si o MA parazita si cum se poate elimina ea?
Observatia de la punctul anterior ramane valabila.Daca apar ambele modulatii simultan,apare o asimetrie a spectrului de amplitudini fata de purtatoare.
7.Cum se poate determina caracteristica unui modulator MA utilizand numai un voltmetru de valori de varf?
In aceste conditii,mesajul poate fi reconstituit chiar din varfuri, fiind continut in semnalul modulator. Deci semnalul purtator poate fi reconstituit prin varfurile indicate de milivoltmetru.
8.Cum se poate determina caracteristica unui modulator MA utilizand numai un voltmetru cu valori efective?
Se masoara valorile efective ale componentelor spectrale.Purtatoarele laterale contin mesajul.
5.Aplicatii
1.La masurarea cu osciloscopul a unui semnal MA,se gasesc:
![]() Se cere
valoarea eficace.
Se cere
valoarea eficace.
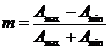 ,de unde rezulta m=0.8.
,de unde rezulta m=0.8.
![]()
2.La masurarea cu milivoltmetrul selectiv a unui semnal MA,se constata ca nivelul purtatoarei este cu 20dB mai mare decat al componentelor laterale.Se cere m.
Transpunem diferenta anterioara din dB intr-un raport adimensional:
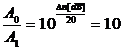
Pe de alta parte,avem
relatia 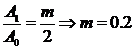
Copyright © 2025 - Toate drepturile rezervate