PROCESE CONDUSE

PROCESE CONDUSE

Ce este un sistem fizic si ce este un proces fizic/tehnic (industrial)? Precizati modul in acre poate fi caracterizat un sistem /proces fizic/tehnic (cu referire si la fig.3.1-2). Dati cateva exemple de procese tehnice (industriale).

Procesul fizic PF) reprezinta un ansamblu de transformari care caracterizeaza obiecte si fenomene interconectate - potrivit unei anumite structuri - si care sunt vazute in evolutia lor temporala. Desfasurarea unui PF implica fenomene de transfer de materie (masa si energie). In fig.3.1-1 sunt sintetizate diferitele forme de prezentare a materiei.

Sistemul fizic (SF) reprezinta ansamblul material in care se desfasoara un PF. Vazut ca sistem, in relatia sa cu mediul inconjurator, SF poate fi caracterizat prin doua categorii de marimi, fig.3.1-2:

- marimi de intrare, notate in general prin vectorul marimilor de intrare u(t) sau u(t), prin intermediul carora se influenteaza din exterior evolutia in timp a SF;

- marimi de iesire, notate in general prin vectorul marimilor de iesire y(t) sau y(t), prin intermediul carora se caracterizeaza evolutia in timp a SF.

Marimile de intrare si de iesire din sistem (proces) se categorisesc functie de modul lor de variatie in timp (asupra acestei categorisiri se va reveni succinct in subparagraful 3.1.2).

Evolutia in timp (variabila independenta, t) a unui SF - vazuta prin evolutia celor doua categorii de marimi - se supune principiului cauzalitatii, conform caruia:

evolutia sistemului este directionata in sensul trecut - prezent - viitor;

evolutia iesirilor y(t) este cauzata de evolutia intrarilor u(t) si a starii initiale in care se afla

sistemul si nu invers.

Procesele de transfer care au loc in SF sunt insotite de fenomene de acumulare, de transfer si de disipare a materiei si energiei care se deruleaza in timp. Corespunzator, se spune ca SF prezinta o dinamica proprie. Dinamica unui sistem fizic poate fi caracterizata complet prin intermediul marimilor de stare ale SF; evolutia marimilor de stare va fi caracterizata prin intermediul variabilelor de stare, notate cu x(t) sau x(t)

Observatie. Marimile de stare ale SF sunt acele marimi care prin valorile lor momentane definesc situatia sau starea in care se afla SF in acel moment de timp. Cunoasterea starii SF la un moment dat , permite si aprecierea tendintelor de evolutie ulterioara a SF. Cum trecerea de la o stare la alta a SF nu poate fi instantanee, rezulta ca marimile de stare ale SF trebuie sa fie marimi continue in timp si cu valoare continua.

Ansamblul marimilor de intrare u(t), de stare x(t) si de iesire y(t) ale unui SF poarta denumire de marimi caracteristice ale SF, notate sau .

Procese tehnice (industriale). Ca sistem fizic, un proces tehnic - industrial/neindustrial, de laborator sau chiar aplicatie de proces "domestic" (casnic) - reprezinta un ansamblu de fenomene de transfer de masa, energie si informatie oriente spre realizarea unui scop bine precizat; in particular acest scop poate fi un produs bine definit, de exemplu subansamblurile unui autovehicul si autovehicolul in ansamblu).

Daca procesul (tehnic) are ca rezultat un produs concret cu o anumita structura si proprietati bine determinate, rezultate din conducerea procesului (de fabricatie), acesta va fi denumit process industrial Exemple de procese tehnice industriale

- producerea si conversia diferitelor forme de energie;

- fabricarea unor produse chimice, farmaceutice si conexe;

- fabricarea diferitelor produse alimentare,

- fabricarea de echipamente si utilaje pentru diferite domenii industriale de prelucrare a materialelor,

- fabricarea unor bunuri de larg consum (inclsiv autovehicule) s.a..

25. Care este reprezentarea schematica a unui proces tehnic (industrial); definiti marimi caracteristice ale unui PC (cu referire si la fig.3.1.3).

Schematic un proces industrial poate fi reprezentat sub forma unui bloc (schema bloc), ca in figura 3.1-3. Se remarca ca la nivelul proceselor industriale se pot manifesta concomitent mai multe categorii de marimi de intrare si de iesire

Structura procesului este evidentiata de cadrul dreptunghiular iar marimi specifice sunt evidentiate prin segmente orientate.

Comenzile sunt semnalele de intrare prin intermediul carora se influenteaza evolutia in sensul dorit al procesului; Prin intermediul semnalelor de iesire se poate urmarii evolutia procesului (simbolizarea poate fi diferita in diferite carti).

Semnalele de intrare si semnalele de iesire pot fi

semnale analogice, notate in continuare cu (simbolizare standard):

u( t ) sau u(t ) - intrare / intrari analogice; ele se mai noteaza si in forma u(t) z( t )sau z( t ) - iesire / iesiri analogice; ele se mai noteaza si in forma z(t); masura acestor marimi se marcheaza cu y( t )sau y( t )sau y(t) (iesiri masurate).

semnale logice, notate in continuare cu:

e( t ) sau e( t ) - intrare / intrari logice; ele se mai noteaza si in forma e(t); s( t ) sau s( t ) - iesire / iesiri logice; ele se mai noteaza si in forma s(t)

Abaterea procesului de la evolutia dorita se datoreaza efectelor perturbatoare care adeseori pot fi evidentiate prin perturbatiile (aici externe) care actioneaza asupra procesului. Actiunea acestora poate fi caracterizata sub forma unor marimi de perturbatie v( t ) sau v( t ) marcate in fig.3.1 distinct (ele se mai noteaza si in forma v(t)). Diferitele tipuri de perturbatii care pot actiona asupra proceselor vor fi detaliate in paragraful 3.2.

Structura functionala a procesului poate fi caracterizata cantitativ si calitativ prin diferite categorii de operatori.

In multe situatii d.p.d.v. informational cele doua categorii de semnale se pot delimta si trata separat; astfel se poate vorbi de o parte a procesului cu semnale continuale si de o parte a procesului cu semnale logice

26. Descompunerea procesului in sub-procese. Ce este un proces fara interactiuni (interconexiuni) (cu referire la fig. 3.1.4)? Prin ce se manifesta efectele de interconectare la nivelul unor SF (cu referire la fig. 3.1.5) ?

C. Descompunerea procesului (sistemului) in subprocese (subsisteme). Pentru simplificarea caracterizarii matematice si ulterior pentru simplificarea dezvoltarii unei structuri de conducere automata este/poate fi utila descompunerea sistemului (procesui) pe subsisteme informationale cat mai simple si pe cat posibil autonome, fara efecte de cuplare intre subsistemele astfel create.

Printr-un sistem / proces fara interactiuni se intelege un sistem pentru care fiecare din iesirile PC este determinata de o singura intrare a acestuia (intrarea ui(t) determina doar evolutia iesirii yi(t)); acest lucru este insa arareori posibil. In figura 3.4-a este prezentat un proces condus (PC) fara interactiuni, cu intrarile semnale analogice; corespunzator si numarul intrarilor este egal cu numarul iesirilor (in numar de r), cele i= 1,.., r canale ale procesului, fiind 'autonome una in raport cu cealalta'.

In fig. 3.1-4-b este prezentat un proces cu semnale analogice caracterizat prin interactiuni intre diferitele canale uI yj; in acest caz numarul intrarilor (r) si numarul iesirilor din proces (notate cu q) pot fi diferite. Daca interactiunile dintre diferitele canale sunt slabe, atunci, deseori aceste

procese pot fi considerate ca aproape autonome.

D. Efectele de cuplare(interconectare). Efectele de cuplare intre diferitele subsisteme din cadrul procesului se manifesta la interconectarea subsistemelor ce compun procesul condus (in special al subproceselor, de exemplu interconectarea cuplarea Element de Executie - Proces Tehnic) si care prin cuplare, realizeaza procesul in ansamblu.

Astfel, la interconectarea subsistemelor fizice (fig.3.1) se constata ca (adeseori, de cele mai multe ori) ansamblul modelelor matematice aferente subsistemelor fizice considerate izolate - echivalent cu "functionarea in gol" ale acestor subsisteme, fig.3.1-5 ec. (1) si (2) - se dovedeste insuficient pentru caracterizarea matematica completa a comportarii sistemului realizat prin interconectare, fiind necesara luarea in considerare a ecuatiilor de legatura (de interconexiune) care caracterizeaza influentele reciproce dintre subsistemele fizice cuplate, fig.3.1-5 ec. (1) (2) si (3).

In masura in care ecuatiile de legatura pot fi neglijate, regimul de functionare "in sarcina" a subsistemelor SF1 si SF2 fiind aproximabil prin regimul de functionare "in gol " ansamblul MM ale subsistemelor componente (considerate izolate) va putea aproxima suficient de bine comprtarea sistemului in amsamblu. In aceste context se vorbeste despre separabilitatea informationala a sistemului pe subsistemele componente cuplarea subsistemelor (informationale) se realizeaza pe baza unor relatii specifice diferitelor tipuri de conexiuni (serie, paralel, cu reactie).

Definirea sistemica a unui proces. Marimi de stare. Legatura dintre conceptul de sistem fizic (SF) si sistem dinamic (SD).

In vederea dezvoltarii unui SCA, procesul tehnic condus trebuie definit din punct de vedere sistemic si trebuie cunoscute principalele sale proprietati. In sensul automaticii clasice, in vederea descrierii cantitative si calitative a oricarui sistem este necesara determinarea unui (unor) model(e) matematic(e) (MM) asociat(e). Constructia modelului matematic (MM) aferent unui SF are la baza definirea structurii sistemului fizic (procesului) si a marimilor sale caracteristice, de intrare, de iesire si de stare.

Pentru partea continuala a SF (procesului tehnic) alegerea marimilor de stare, care trebuie sa respecte urmatoarele cerinte

- marimile sa aiba variatie continua in timp;

- marimile sa caracterizeze fenomenele de acumulare, de transformare, de transfer si de disipare a materiei in SF.

Un SF caracterizat prin intermediul modelului sau matematic (MM) conduce la conceptul de sistem dinamic (SD) sau de sistem abstract (reprezentare informationala). In acest context, SD este un concept matematic definit prin axiome referitoare la:

categorii de multimi si clase de functii, prin intermediul carora se caracterizeaza variabila independenta t si marimile caracteristice ale SF;

operatori (functionale) prin intermediul carora se caracterizeaza dependentele structurale dintre marimile caracteristice ale SF (a se vedea dependentele dintre subsistemele fizice SF 1, SF2 si SF n din fig.3.2).

Pentru cazul unui sistem cu o singura intrare si o singura iesire legatura dintre SF si MM asociat (SD) este data in fig.3.1-6. Timpul t este variabila independenta (continua); in caracterizarea matematica a sistemelor cu timp discret timpul poate lua si valori discrete (par.3.1.3).

Exista doua categorii de baza de MM asociabile unui SF (SD):

- MM intrare-stare-isire (MM-ISI);

- MM intrare-iesire (MM-II).

(a) MM intrare-stare-isire (MM-ISI) au rolul de a evidentia stuctura informationala interna a SF (proceului) sub forma unei reprezentari compuse de forma:

u(t) x(t) y(t)

Aceasta reprezentare poarta si denumirea de reprezentare structurala a SD. Forma generala a MM-ISI aferenta unui SD cu timp continuu cu o intrare u(t) si o iesire y(t) (sistem SI-SO, Single Input-Single Output)este data de rel.(3.1-2):

x&( t ) A x( t ) bu( t ) - ecuatia de stare,

y( t ) cT x( t ) d u( t ) - ecuatia iesirii ; (3.1-2)

marimile de stare x( t ) sunt marimile interne ale SF (SD).

(a)     MM intrare-iesire (MM-II). Eliminand in rel.(3.1-2) marimile de stare se poate explicita dependenta nemijlocita intrare - iesire aferenta (SD) SF:

intrare [u(t) ] → iesire [y(t)] ,

care corespunde unui model matematic intrare-iesire (MM-II).

Categorisirea sistemelor dinamice si a sistemelor fizice. Puncte de vedere (criterii) de clasificare (cu referire la tabelul 3.1-3 si la fig. 3.1.7)

A. Clasificarea semnalelor si variabilelor. Prin semnal se intelege o marime fizica vazuta ca support purtator al informatiei referitoare la un sistem. Semnalele sunt caracterizate prin intermediul unor functii, u, de variabila timp t

Functia u este o aplicatie de forma:

u :T U   

care asociaza fiecarui "moment de timp" t T, T - multimea momentelor de timp, un element u(t) din multimea U a valorilor functiei de timp.

Ansamblul functiilor de intrare (in general de stare sau de iesire) posibile notate cu U (respectiv X sau Y

U

constituie clasa functiilor de intrare (de stare sau de iesire). In tabelul 3.1-3 se prezinta o clasificare semnalelor functie de caracterul multimilor din relatia (3.1-6):

(a) Dupa caracterul multimii T , al momentelor de timp se disting (tabelul 3.1-3, col. (1), (2), (3)):

semnale continue in timp (cu timp continuu), pentru care T este un segment compact,

semnale discontinue in timp, pentru care:

-semnale discrete in timp (cu timp discret), pentru care T este o multime de valori discrete

(b) Dupa caracterul multimii U se disting (tabelul 3.1-3, linia (2)):

Semnale cu valoare continua, pentru care U este un segment compact (tabelul 3.1-3, linia (1));

Semnale cu valoare cuantizata, pentru care U este o multime numarabila, cu valori discrete;

Aceste semnale se manifesta cu preponderenta in cazul sistemelor de reglare automata,

Semnale logice binare (discontinue in timp), caracterizate de doua stari posibile, 0 sau 1 (de exemplu semnalul din col.(2), linia (2), vazut in evolutia temporala (secventa de valori 0 si 1)); celor doua stari li se asociaza valorile de (1)=adevarat/ conectat (0)=fals/deconectat s.a.

Aceste semnale sunt specifice sistemelor de comanda automata.

Semnalele continue in timp si cu valoare continua se numesc semnale continue; ele sunt specifice sistemelor fizice continuale si DC realizate cu echipamente clasice, analogice (electrice, electronice, mecanice, hidraulice, pneumatice).

Semnalele cu timp discret cu valoare cuantizata (si apoi codificata) sunt specifice DC cu timp discret numerice (digitale).

Semnalele cu timp continuu cu valoare cuantizata sunt prezente in cadrul SCA cu DC cu timp discret ca extensii continue ale semnalelor cu timp discret.

Semnalele discontinue in timp sunt prezente in constructii de DC electronice.

(c) Dupa modul de prezentare a informatiei continute in semnal se disting:

Semnale necodificate: purtatoarea continutului informatiei este "valoarea semnalului" la un moment dat (semnale modulate in amplitudine) sau durata lui (la o amplitudine constanta) (semnale modulate in durata, tabelul 3.1-3);

Semnale codificate: purtatoarea continutului informatiei il poate reprezinta:

1. numarul de impulsuri intr-un interval de timp dat (reprezentarea (1)),

2. codificarea modului de succesiune a impulsurilor la un moment de timp dat (reprezentarea paralel, (2-a)) sau intr-un interval de timp dat (Tq) (reprezentarea serie, (2-b)).

In fig.3.1-7 sunt redate diferite modalitati de codificare a informatiei cuprinse in esantionul de la momentul tk (u(tk)=uk) al semnalului continuu u(t) ū(tk) reprezinta valoarea cuantizata a

esantionului, iar u⁼( t ) k semnifica "valoarea" codificata aferenta.

Semnalele discrete in timp, cu valoarea cuantizata si apoi codificata sunt specifice prelucrarii numerice a informatiei la utilizarea in conducere a calculatoarelor numerice.

Caracterizarea determinista intrare-iesire a sistemelor. Cazul liniar, monovariabil, cu timp continuu si cu timp discret.

Un sistem poate fi "vazut" numai din punctul de vedere al dependentei cauzale dintre intrarile si iesirile sale (directionata in sensul evolutiei trecut → prezent → viitor). Se vorbeste despre caracterizarea intrare-iesire a sistemului. Pentru aceasta caracterizare se apeleaza modelele matematice intrare-iesire (MM-II). In literatura, definirea riguroasa a caracterizarii prin MM-II este de asemeni axiomatizata.

Pentru cazul SLI monovariabil (SISO), fig.3.2-3 , MM-II aferente se expliciteaza dupa cum urmeaza.

Fig.3.2-3. Sistem monovariabil la intrare si iesire (SISO).

A. In cazul SD-C liniar si invariant, MM-II este o ecuatie diferentiala (liniara cu coeficienti constanti) de forma (3.2-14):

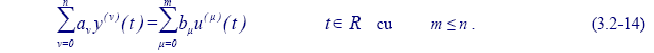
B. In cazul SD-D liniar si invariant, MM-II este o ecuatie recurenta (cu timp discret) cu coeficienti constanti de forma (relatia scrisa in anticipari):

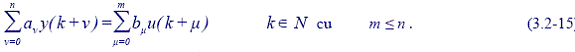
Exista o multitudine de posibilitati de atasare a unui MM-timp discret la un SD (SF) cu timp continuu. Ecuatia (3.2-14) descrie comportarea sistemului numai la momentele de timp kTe (momentele de esantionare) nu si intre aceste momente, fig.3.2-1, 3.2-2. Ca urmare alegerea perioadei de esantionare Te va juca un rol deosebit in caracterizarea in timp discret a unui sistem continual

Schimbarea valorii ei determina:

- schimbarea valorii coeficientilor a ν ,b μ si cu aceasta a proprietatilor sistemului,

- poate afecta si valorile m si n (cere pot deveni diferite decat cele ale MM continual, de baza)

In relatiile (3.2-14), (3.2-15) conditia m ≤ n reprezinta o forma de explicitare a conditia de cauzalitate (in sensul intrare iesire) a sistemului.

Unele precizari referitoare la conceptele de teoria sistemelor introduce in acest paragraf:

1. In general, cele doua caracterizari matematice - MM-ISI si respectiv MM-II - trebuie sa aiba acelasi continut. Acest lucru este valabil (cel putin din punct de vedere matematic) in redarea directa a conexiunii intrare → iesire. Exista insa si clase particulare de sisteme, cu anumite proprietati. structurale, pentru care cele doua reprezentari nu sunt echivalente; este de retinut faptul ca reprezentarea prin MM-ISI este mai cuprinzatoare, evidentiind mai multe proprietati.

2. Adeseori tratarea matematica a SF bazata pe MM-II este mai simpla decat tratarea prin MM-ISI si caracterizarea prin MM-II satisface cerintele de realizare a unui SCA dupa iesire. Abordarea problematicii conducerii automate bazata pe reprezentarea intrare-iesire corespunde abordarii clasice a reglarii automate.

3. In cazul caracterizarii intrare-iesire a sistemelor se vorbeste si de conceptul de cutie neagra black box). La acest concept se asociaza si determinarea unui MM-II pe baza prelucrarii masurarilor legate de evolutia in regim dinamic a intrarii si iesirii (identificarea experimentala a procesului).

4. Modelele matematice prezentate sunt modele deterministe.

30. Etapele determinarii pe cale analitica a MM asociate sistemelor fizice (cu referire la fig. 3.2.5)

Pe cale analitica (constructia modelului), bazat pe "cunostinte a priori" despre SF; ea poarta si denumirea de identificare analitica (IA). Aspecte legate de determinarea pe cale analitica a modelelor matematice bazat pe legile fizico-chimice ce caracterizeaza fenomenele din procesele tehnice vor fi reluate in par.3.4.

Determinarea pe cale analitica a MM este o cale a-priori de stabilire a MM aferent unui PC si presupune parcurgerea mai multor etape

- Definirea PC d.p.d.v. al conducerii (intrari, iesiri, stari) si al relatiilor sale cu mediul inconjurator; stabilirea ipotezelor simplificatoare care pot fi adoptate la scrierea MM.

- Scrierea ecuatiilor de bilant de materie (mase, energii) aferente PC, caracterizarea interconexiunilor din proces, intocmirea schemei bloc informationale aferente; ca rezultat se obtine MM primar aferent PC sub forma unor ecuatii diferentiale; utilizarea nemijlocita a acestora se dovedeste adeseori greoaie.

- Precizarea ipotezelor simplificatoare in care MM primar poate fi adus la forme mai simple, prin:

- liniarizarea ecuatiilor neliniare (liniarizabile) sau omiterea unor neliniaritati neesentiale; concentrarea parametrilor;

- "reducerea ordinului" MM liniarizat prin renuntarea la evidentierea efectelor unor constante de timp foarte mici.

- Reordonarea ecuatiilor in vederea stabilirii formei finale a MM; adeseori se dovedeste utila intocmirea schemei bloc informationale aferente. MM astfel obtinut poate servi ca baza pentru:

- determinarea valorilor parametrilor SF pe cale analitica sau experimental-analitica;

- fundamentarea unori proceduri de IE a PC.

- Verificarea corectitudinii MM si validarea acestuia. Aceasta operatie trebuie derulata in acord cu scopul pentru care a fost creat MM. Procedeul de validare va depinde de informatiile disponibile relative la PC real.

31. Etapele determinarii pe cale experimentala a MM asociate sistemelor fizice (cu referire la fig. 3.2.5 si 3.2-6).

Pe cale experimentala (experimental-analitica), bazat pe "informatii ulterioare" despre SF; ea poarta si denumirea de identificare experimentala (IE).

Determinarea experimentala (identificarea experimentala, IE) a MM aferenta PC IE reprezinta o etapa de cunoastere a-posteriori a MM. MM aferent PC va fi determinat prin IE pe urmatoarele baze:

- Informatiile primare furnizate de o IA efectuata a-priori,

- Rezultate strict experimentale; in acest caz cunostintele primare despre PC sunt minimale, MM poarta denumirea de MM black-box sau grey-box..

Intr-o aplicatie de identificare experimentala, metoda de identificare va fi adoptata dependent de cunostintele primare despre proces, de aparatura la dispozitie, de metodele de prelucrare a informatiei (algoritmi) disponibile si de experienta de identificare (incluzand si algoritmii de prelucrare a informatiei primare).

Pentru exemplificare, principalele etapele ale unei IE sunt urmatoarele:

Etapa I-a. Alegerea metodei de IE, a metodelor de prelucrare analitica si a echipamentelor de IE. Organizarea experimentelor de IE.

Etapa a II-a. Generarea semnalului de proba: GST - generator de semnal de test uT(t); efectuarea masurarilor de regim dinamic; inregistrarea simultana a marimilor u(t) si y(t), eventual si a altor marimi, tratarea inregistrarilor (filtrarea de zgomote suprapuse, extragerea componentelor continue, extragerea trendurilor s.a.).

Etapa a III-a. Prelucrarea rezultatelor primare bazat pe cunostintele primare relative la structura MM valori orientative ale parametrilor, se prelucreaza inregistrarile pentru determinarea:

- parametrilor MM la o structura acceptata a MM;

- MM neparametric, urmata apoi de

-prelucrarea MM neparametric la forma MM parametric.

Etapa a IV-a. Verificarea corectitudinii si validarea MM obtinut in concordanta cu scopul pentru care a fost determinat MM.

Sunt utile cateva precizari    referitoare la practica IE a PC:

(1) IE a unui PC poate fi efectuata cu functionarea PC:

cu functionarea PC in circuit deschis, in afara buclei de reglare, fig.3.2-6 (a);

cu functionarea PC conectat in bucla de reglare, fig.3.2-6 (b); in acest caz insa, determinarea MM aferent PC este supusa unor restrictii.

(2) MM primare obtinute prin IE sunt adesori MM neparametrice si au urmatoarele particularitati

- Valabiliatea MM determinate experimental este limitata, legata de punctul de functionare in care s-a facut IE;

- MM neparametrice sunt modele care caracterizeaza global PC in relatia u → y, fara evidentierea structurii interne a PC; ca efect, MM parametrice asociate vor avea parametri care pot sa nu caracterizeze parametrii interni ai PC;

- MM parametrice care se construiesc sunt relativ simple; si ele au adeseori structura construita orientat spre a fi usor utilizabile in scopul propus.

(3) Identificarea experimentala presupune adeseori prelucrarea primara a semnalului preluat din proces; acest lucru presupune alegerea adecvata a perioadei de esantionare, prefiltrarea semnalului (inclusiv extragerea unor componente continue legate de punctul de functionare al PC s.a.).

(4) MM obtinut prin identificare poate fi cu timp continuu sau cu timp discret, dependent de tehnologia de identificare si in acord cu scopul pentru care s-a determinat MM. Conversia MM continuale in MM cu timp discret si invers are la baza tehnici si relatii bine precizate, valabile in anumite conitii specifice.

(5) MM determinat se valideaza in acord cu scopul propus prin verificarea concordantei dintre evolutia MM si evolutia reala a PC. In acest scop se poate utiliza urmatoarele tehnici: - simularea pe calculator (analogic sau numeric) a comportamentului MM; - realizarea unor modele la scara redusa ale PC pe baza MM determinat si studiul comportamentului acestora s.a.

Detalierile de identificare si de modelare trebuie aduse intodeauna in acord cu scopul pentru care se construieste MM. Acesta poate fi: - pur informativ, pentru o mai buna cunoastere a PC si (eventual) imbunatatirea calitatii conducerii; - proiectarea structurilor si a algoritmilor de conducere a PC; rezultatul proiectarii si, in consecinta, performantele SCA vor depinde de corectitudinea MM al PC.

32. Modele matematice neliniare si modele matematice liniarizate. Esenta liniarizarii. Tratati un caz de liniarizare.

In cele mai multe ori situatii din practica, dependentele dintre marimile caracteristice ale SF

sunt neliniare (cu neliniaritati), ceea ce solicita apelarea unor MM neliniare. In anumite conditii, aceste

dependente pot fi caracterizate (local) prin dependente de aproximare liniare; operatia de inlocuire a

unui MM neliniar (NL) cu un MM liniarizat (Ln), de aproximare, poarta denumirea de liniarizare.

Esenta liniarizarii. Valabilitatea MM-Ln este de regula restransa la domenii din jurul unor puncte

de functionare (de liniarizare). Obisnuit, punctele de liniarizare corespund unor regimuri

reprezentative de functionare ale sistemului, numite puncte de functionare stationara constanta

(p.d.f.s.c.). P.d.f.s.c. caracterizeaza ansamblul valorilor marimilor caracteristice care corespund

functionarii SF (SD) in regimul stationar constant (RSC) specificat. P.d.f.s.c. ale unui SF se

marcheaza prin coordonatelor lor, in forma uzuala A0(u0, y0, x0) sau A(u∞, y∞, x∞)

Un SF (SD) stabil (conditiile de stabilitate sunt detaliate in lucrarile de teoria sistemelor,

ingineria reglarii automate s.a.) se afla in RSC, atunci cand marimile sale caracteristice nu variaza in

timp. D.p.d.v. matematic, stabilirea unui RSC revine la anularea efectelor de derivare si de integrare

din sistem. Referitor la MM-ISI si MM-II de forma (3.2-1) si (3.2-2), aceasta revine la asigurarea

urmatoarelor conditii:

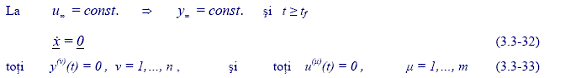
tf reprezinta timpul dupa care in sistem sa stabilizat RSC (sistemul fiind considerat stabil). Valorile de RSC se marcheaza cu indice inferior (de exemplu,

Ca urmare, in RSC, MM-ISI se transforma in dependentele de regim stationar constant:

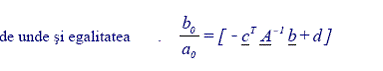
Plecand de la MM-NL cu variabilele caracteristice , prin liniarizare se va determina un MM liniarizat (MM-Ln) care va avea ca variabile proprii, cresterile variabilelor de baza in raport cu coordonatele p.d.f.s.c. de liniarizare , notate prin:

Δu(t)=u(t)-u0 , Δy(t)=y(t)-y0 , Δx(t)=x(t)-x0

Observatii: 1. Pentru cazul particular, in care A0(0, 0, 0) (punctul de repaus al sistemului) se obtine:

Δu(t) = u(t) , Δy(t) = y(t) , Δx(t) = x(t) .

(2) Aplicarea procedurii de liniarizare. Cazuri remarcabile de liniarizare. In practica se pot defini mai multe situatii tipice de aplicare a procedurii de liniarizare. Acceptand - intr-o prima faza - ca neliniaritatea SNL este caracterizata printr-un MM-NL analitic, atunci MM-Ln se obtine prin dezvoltarea MM-NL in serie Taylor, in vecinatatea p.d.f.s.c. de liniarizare A0 si neglijarea termenilor care contin cresterile de ordin superior ale variabilelor

a.     Liniarizarea MM-NL aferent unui sistem monovariabil, pentru care MM-NL, dat de rel.(3.3-36):

y(t) = f(u(t))

este cunoscut sub forma analitica neliniara dar derivabila pe portiuni. Ca si caz particular remarcabil care va rezulta din procedeul general descris este si cel in care MM-NL este cunoscut sub forma grafica a CS neliniare aferente SF.

Prin dezvoltarea rel.(3.3-36) in serie Taylor, in jurul p.d.f.s.c. A0(u0, y0), se obtine:

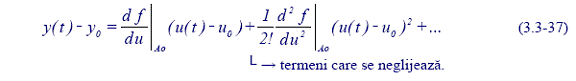
Interpretarea grafica a relatiei este data in fig.3.3-9; k este o marime cu dimensiune:

k = tg α <k> = <Δy>/<Δu>

A0(u0, y0), este punctul de liniarizare iar A(u, y) punctul curent de functionare a sistemului.

Prin liniarizare, punctul de functionare este translatat (informational) din A in A'(u, y'), segmentul [AA' ]     fiind o (posibila) masura a erorii de liniarizare

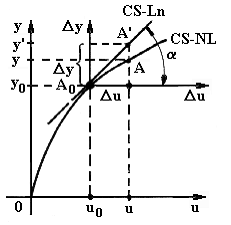
Fig.3.3-9. Interpretarea grafica a liniarizarii

Caracterizarea in domeniul operational al sistemelor liniare cu Parametri concentrati. Definirea functiei de transfer pentru sistemele cu timp continuu.

Se considera SLI monovariabil, cu timp continuu, caracterizat prin MM-II de forma:

Functia de transfer (f.d.t.) a unui sistem liniar, notata H(s), este definita ca raportul dintre imaginea Laplace a marimii de iesire y(s) si imaginea Laplace a marimii de intrare u(s), sistemul fiind considerat in conditii initiale nule:

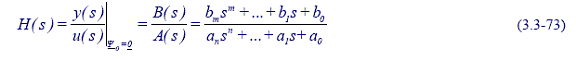
Corespunzator, relatia (3.3-62) se poate rescrie in forma:

y( s ) H( s )u( s )   

Observatie: relatia (3.3-72) sta la baza unei metode de calcul al raspunsului SLI.

Pentru caracterizarea dinamicii SF (PC) continue se utilizeaza constantele de timp, notate (de regula) cu T. Evidentiere in MM-II din domeniul timp si din domeniul operational (f.d.t.) a constantelor de timp este foarte utila, dand indicatii asupra caracterului lent/rapid al procesului.

In vederea exemplificarii acestei evidentieri se considera SF cu MM de forma:

prin impartire cu a0 si reordonare se obtine:

34. Ce sunt perturbatiile si cum se clasifica acestea. Exemplificati succint esenta perturbatiilor pe o aplicatie de proces (actiunea diferitelor tipuri de perturbatii).

Perturbatiile reprezinta ansamblul influentelor externe sau interne care pot determina abaterea evolutiei procesului de la evolutia dorita. Perturbatiile externe dar in anumite conditii si cele interne actioneaza ca rezultat al interactiunii sistemului (procesului) cu mediul inconjurator; perturbatiile interne actioneaza si ca rezultat al deteriorarii proprietatilor initiale ale sistemului

In functie de originea lor perturbatiile se pot impartii in mai multe moduri:

Perturbatii externe (sau exogene) Sunt categorii de perturbatii care actioneaza dinspre exteriorul procesului asupra desfasurarii acestuia (de exemplu, pentru temperatura dintr-o camera, c temperatura exterioara ext constituie o perturbatie externa, exogena). Perturbatiile externe pot fi categorisite in mai multe tipuri:

- perturbatii de tip sarcina: se manifesta sub forma unor marimi de intrare suplimentare care conduc la abaterea functionarii sistemului de la evolutia dorita.

Ca exemplu se poate considera o masina care circula pe o sosea orizontala si - la un moment dat - intra pe o panta (in sus); acest lucru impune un efort suplimentar la nivelul motorului astfel ca - pentru mentinerea vitezei - conducatorul autvehicolului va fi obligat sa accelereze (si alte manevre sunt posibile).

- perturbatii parametrice: reprezinta actiuni perturbatoare externe care modifica valorile unor parametri ai sistemului (procesului); uneori aceste perturbatii se manifesta si in modificarea structurii procesului.

- perturbatii parazite, cu efect adeseori aleator (de exemplu perturbatiile ce pot apare pe canalele de masura analogice).

Perturbatii interne (sau endogene) reprezinta efectul unor actiuni care se manifesta in interiorul procesului asupra desfasurarii acestuia si determina modificari ale stucturii sau ale valorilor parametrilor sistemului. Perturbatiile interne pot fi categorisite in :

perturbatii parametrice,

perturbatii de tip structura,

perturbatii parazite.

De exemplu, pentru temperatura dintr-o camera c , temperatura agentului de incalzire - de exemplu temperature apei calde din instalatia de incalzire centrala - este un parametru a carei modificare (de exemplu scadere) are efecte negative asupra temperaturii din camera si constituie o perturbatie interioara a sistemului de incalzire.

1. Perturbatiile de tip sarcina corespund incarcarilor variabile la care poate fi supus procesul condus (momentul rezistent suplimentar, puterea suplimentara solicitata, caldura pierduta s.a). Aceste perturbatii sunt evidentiabile direct ca marime de perturbatie, marcate cu v(t)

Perturbatiile parazite corespund unor factori externi sau interni, cu caracter aleator sau persistent, care se manifesta sub forma unor zgomote, drifturi s.a..

De regula, aceste doua categorii de perturbatii nu afecteaza forma dependentelor intrare-iesire ale PC (MM aferente PC). Ele pot fi surprinse sub forma unei marimi de perturbatie v(t)

Perturbatiile parametrice (sau chiar de structura) corespund unor cauze interne sau externe si au drept rezultat modificarea valorilor parametrilor care apar in MM ce caracterizeaza PC. Uneori aceste perturbatii sunt datorate si fenomenelor de imbatranire si de uzura.

Perturbatiile de structura corespund unor cauze interne sau externe care au ca efect modificarea structurii SF (PC) si prin aceasta afecteaza MM ce caracterizeaza PC; dupa caz pot apare si modificari ale valorilor unor parametrii.

35. Caracterizati prin exemple procese specifice diferitelor aplicatii industriale din cadrul celor prezentate la curs (se va specifica prin subiectul concretizat la examen):

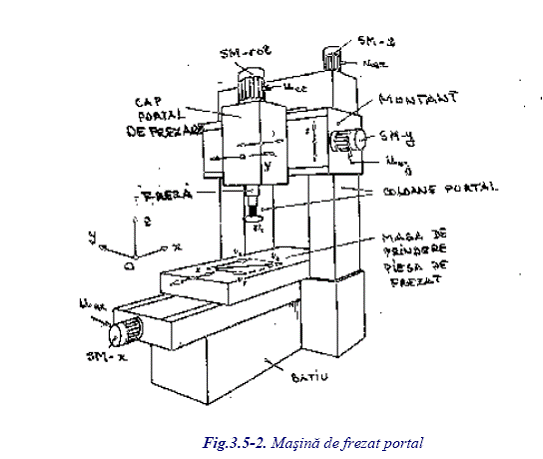
masina de frezat tip portal, fig. 3.5-2 si 3.5-3.

generator sincron antrenat de catre o turbina hidraulica, cuplat la sistemul energetic, fig.3.5.5 , 3.5.6 si 3.5.7.

masina de spalat automata programabila, fig.3.5.9 si 3.5.10.

instalatia de incalzire a unei cladiri cu mai multe incinte; fig.3.5.11 si 3.5.12,

reactor de amestecare neutralizare a apelor reziduale, fig.3.5-15 si 3.5.16,

sistem de transport cu conveior , fig.3.3.17,

Analizati si detaliati in vederea conducerii descompunerea procesului pe subsisteme fizice si pe subsisteme informationale.

A. Masina de frezat tip portal. Schema functionala (de principiu) aferenta unei freze portal cu

prelucrare dupa trei axe (in trei coordinate) este prezentata in fig. 3.5-2. Piesa de prelucrat este fixata

pe masa masinii (batiu) care poate fi deplasata dupa axa x (inainte-inapoi) cu ajutorul unui servomotor

SM-x. Capul de prelucrare este fixat pe un montant si se poate deplasa dupa axa y (dreapta-stanga),

antrenat de servomotorul SM-y. Montantul cu capul de frezare se poate deplasa dupa axa z (sus-jos pe

coloana portal). Prin miscarea de rotatie a frezei se asigura indepartarea materialului din piesa de

prelucrat. Procesul tehnologic poarta denumirea de frezare. Deplasarea dupa axa z a capului de fixare a

frezei si miscarea de rotatie a frezei este asigurata de servomotoarele SM-z si SM-rot.

Frezele portal sunt destinate prelucrarii unor piese plane dupa anumite contururi. Acest lucru

se realizeaza prin deplasarea relativa (simultana si coordonata) dupa axele x y si z ale piesei (masa

masinii) si capului portal (de prelucrare). Aceste deplasari (traiectorii, viteze) impreuna cu deplasarea

pe verticala a capului si cu viteza de rotatie a frezei, vc, sunt fixate din considerente tehnologice

(materialul de prelucrat, volumul de material de indepartat, puterea motoarelor electrice s.a.); atingerea

formei finale a piesei frezate are loc prin mai multe treceri (treceri succesive).

D.p.d.v.d. a conducerii, procesul poate fi descompus pe subprocese (subsisteme), ca in fig.3.5- 3. Astfel, procesul este descompus in cinci subsisteme caracterizate prin urmatoarele marimi caracteristice.

Subsistemul de deplasare dupa axa x a mesei (actionat de SM-x ) are ca marimi caracteristice:

- marime de comanda, ucx - tensiune de comanda a servomotorului SM-x

- marimi de iesire : vx - viteza de deplasare dupa axa Ox,; sx - spatiul strabatut dupa axa x, (pozitia dupa x);

marime de perturbatie (externa): fx - forta rezistenta echivalenta.

Subsistemul de deplasare dupa axa y a capului portal (de frezare). Are structura similara cu a subsistemului de deplasare dupa axa x dar cu o structura mecanica (deci inclusiv MM aferent) diferita:

- marime de comanda , ucy : - tensiunea de comanda a SM-y

- marimi de iesire: vy - viteza de deplasare dupa axa Oy, sy - spatiul strabatut dupa axa Oy, sau pozitia dupa axa z

- marime de perturbatie(externa): fy - forta rezistenta echivalenta, .

Subsistemul de deplasare dupa axa z are ca marimi caracteristice:

- marime de comanda ucz : - tensiune de comanda a SM-z

- marimi de iesire: vz - viteza de deplasare dupa axa Oz,. sz - pozitia frezei dupa axa Oz,.

Subsistemul de antrenare a frezei (SM-rot) si sistemul de reductie(mecanic) si de reglare (electronica) a turatiei are urmatoarele marimi caracteristice:

- marime de comanda : ucc - tensiune de comanda a SM-rot

- marime de iesire: c - viteza de rotatie a frezei

- marime de perturbatie: fc - forta de frezare dependenta de avansurile dupa x, y, z si de materialul

piesei prelucrate.

Subsistemele care asigura serviciile auxiliare ale masinii reprezinta ansamblul subsistemelor care deservesc functionarea frezei si procesul de frezare; din cadrul acestora se mentioneaza explicit:

- sistemul de racire (cu lichid de racire ) la suprafata de frezare (pompa, circuit de racire),

- sistemul de ungere s.a.

B. Generator sincron (GS) antrenat de o turbina hidraulica, cuplat la sistemul energetic (SE)

Schema functionala de principiu a unui astfel de sistem este prezentata in fig. 3.5-5.

Turbina hidraulica este antrenata de catre apa adusa la turbina printr-un sistem de aductiune (fig.3.5-6). Turbina antreneaza un generator sincron GS in care, energia de miscare (manifestata prin rotirea turbinei cu viteza unghiulara =const.; valoarea lui depinde de numarul de poli (p) ai GS, = 2π f/p este convertita in energie electrica la parametrii ug -tensiunea la bornele generatorului, ig curentul debitat, pg -puterea activa si qg puterea reactiva debitate. Energia este produsa sub forma "alternatiuva" la o frecventa constanta (in intreg SE), f = 50 Hz

Ansamblul turbina-generator este un 'sitem de conversie a energiei'; lantul conversiei energetice realizate este urmatorul: energie primara energie cinetica energie electrica

(apa) (T+ GS) (GS= SE)

Pentru reglarea turatiei, a puterii active debitate de catre GS se intervine la nivelul turbinei prin comanda de deschidere-inchidere a aparatului director ucω, care asigura debitul de apa necesar catre turbina. O relatie simplificata aferenta conversiei, este de forma:

La valori =const. si uG=const. modificarea momentului (cuplului) la arborele generatorului (datorata modificarii debitului de apa) conduce la modifcarea curentului debitat (debitabil) de catre GS si in ansamblu, a puterii electrice produse. In vederea reglarii tensiunii la borne uG=const (puterii reactive debitate de catre GS), la nivelul GS se intervine prin intermediul tensiunii de excitatie uE respectiv comanda aferenta acesteia, ucE. Functionarea GS cuplat la sistemul energetic (SE) impune urmatoarele conditii:

- viteza unghiulara constanta corespunzatoare frecventei din SE

f/p in care p - numarul de perechi de poli (electrici) ai GS;

- tensiune la borne constanta uG =constanta, corelata cu puterea reactiva care trebuie furnizata de catre GS catre SE.

- posibilitatea incarcarii GS cu putere activa pG si putere reactiva qG functie de cerintele SE. Frecventa constanta in sistemul energetic se asigura prin mentinerea echilibrului putere ceruta de consumatori (Σ pcerut ) si putere furnizata de centrale Σ pcerut (produsa la nivelul grupurilor SE):

Procesul poate fi reprezentat printr-o schema bloc simplificata ca in fig.3.5-7 in care sunt evidentiate cele doua subsisteme de baza, turbina hidraulica (T) si generatorul sincron (GS) cuplat la SE si serviciile interne (auxiliare) care asigura/deservesc functionarea sistemului.

Se constata ca procesul este multivariabil, prezentand mai multe intrari si mai multe iesiri.

Marimile caracteristice ale 'sistemului Turbina - GS - SE' sunt urmatoarele (fig.3.5-3):

Marimi de intrare cu caracter de comanda

y - pozitia aparatului director, prin care se asigura debitul de apa catre turbina (qa

uE - tensiunea de excitatie la bornele GS.

Marimi de intrare cu caracter perturbator

h - "caderea" amenajarii (diferenta dintre nivelul apei "in amonte" si nivelul apei "in aval" de turbina), fig.3.5-6;

pG , qG - puterile activa si reactiva "ceruta" de catre SE (consumatorii din sistemul energetic).

Marimi de iesire ale 'sistemuluide conversie' (marimi care vor trebui reglate)

uG - tensiunea la bornele GS;

f - frecventa in SE (la bornele GS).

C. Masina de spalat automata programabila (MSA-p) (aplicatie electrocasnica). Constituie o aplicatie electrocasnica prevazuta cu un sistem de comanda combinationala si secventiala si mai multe subsisteme de reglare. Structura unei MSA-p este prezentata in fig 3.5-9. Pentru ca un astfel de produs sa fie vandabil el trebuie sa ofere utilizatorului o varietate mare de facilitati (regimuri de functionare).

Astfel de exemplu, pentru regimul de spalare 'normal', procesul de spalare presupune parcurgerea urmatorului ciclu:

- umplere cuva cu apa (amestec apa calda - apa rece), pana la nivelul maxim admis: (hc

- prespalare la temperatura c1 ( selectabila ) asigurata prin (variante posibile);

- preincalzire, utilizand un rezistor alimentat la 220V c.a.; durata prespalarii tps selectabil,

- evacuare apa uzata prin sistemul de evacuare;

- umplere cuva cu apa, pana la nivelul maxim admis;

- spalare la temperatura constanta c2 (selectabila); durata spalarii tsp - selectabil.

- racire apa inainte de evacuare prin utilizarea unei cantitati de apa rece in adaos;

- evacuarea apei uzate, prin sistemul de evacuare;

- ciclu de clatire cu apa rece;

- centrifugare pe durata de timp limitata;

- uscarea rufelor spalate s.a.m.d..

Procesul poate fi descompus pe subsisteme conform fig. 3.5-10.

Marimile caracteristice ale sistemului sunt urmatoarele:

marimi de intrare: pn - puterea absorbita de elementul de incalzire; (ug - comanda de golire); (uac , uar - comanda umplere apa calda / rece);

marimi de iesire: c - temperatura apei in cuva;

hc - nivelul apei in cuva (este si marime de interconexiune).

Sistemele auxiliare inerent necesare functionarii: sistemul de golire si sistemul de alimentare.

Remarca: la acest exemplu (usor de urmarit) se disting succesiunile de comenzi combinationale si secventiale precum si procesele de reglare a temperaturii apei.

D. Instalatia de incalzire a unei cladiri cu mai multe incinte. Schema de principiu a sistemului de incalzire este prezentata in fig. 3.5-11. Un cazan in care se arde gaz metan incalzeste apa calda din circuitul primar al sistemului de incalzire la temperatura c de cca 85 C.

In scopul mentinerii constante a temperaturii in incinte se actioneaza in final asupra debitului de gaz metan ars in cazan. Fiecare din incinte (grupuri de incinte) este incalzita printr-un circuit secundar conectat la circuitul primar prin intermediul unor robinete cu patru cai R4 - c. In circuitul (circuitele) secundar apa este recirculata cu ajutorul unor pompe de recirculare antrenate de motoare electrice m 1, m 2. Prin amestecarea apei din circuitul primar si al apei din circuitul secundar - realizat in robinetele cu patru cai R4 - c (raportul este asigurat de deschiderea corespunzatoare a robinetului R4-c, prin unghiul de deschidere i determinat la randul lui de comanda de reglare a pozitiei motoarelor

ce actioneaza aceste robinete) - temperatura in incinte i11, i12, . se mentine la valoarea dorita.

Dependent de ipotezele simplificatoare adoptate, procesul poate fi descompus in trei subsisteme informationale cu diferite interconexiuni:

(a) Daca intre incintele incalzite izolatia termica este foarte buna, se poate accepta ca schimbul de caldura intre acestea este neglijabil si in consecinta e obtine schema din fig. 3.5-12 (a)30 (a):

Subsistemul cazan constand din:

- sistemul de ardere;

- sistemul primar de circulatie a apei;

Marimile caracteristice ale acestui subsistem sunt urmatoarele:

g - debitul de gaz ars, reglabil prin robinetul de reglare RR. Acest robinet poate fi:

- cu caracteristica statica comanda-pozitie continua,

- cu caracteristica statica comanda-pozitie cu doua stari stabile: 0 - inchis, 1 - deschis.

c - temperatura apei din cazan (marime de iesire);

Aceste subsisteme sunt deservite de pompele de recirculare antrenate de motoare electrice.

(b) Daca intre incinte are loc un schimb de caldura ansamblul celor doua incinte trebuie tratat ca

sistem multivariabil si se poate descompune sub forma schemei din fig. 3.5-12 (b).

F. Reactor de amestec (1). Reactoarele de amestec (amestecatoare) sunt instalatii (tehnologice) utilizate in industria chimica pentru derularea diferitelor procese chimice; de exemplu in procesele de tratare / neutralizare a apelor reziduale, fabricarea diferitelor produse alimentare, farmaceutice s.a In fig. 3.5-15 este prezentata structura unui astfel de sistem cu trei reactoare utilizate la neutralizarea apelor industriale.

In rezervoarele A si B soseste lichidul cu concentratie acida sau bazica care se abate puternic de la conditia pH - neutral pH = 7 u.). In vederea neutralizarii apelor evacuate, se utilizeaza si un al treilea rezervor C.

- In rezervorul 1 soseste o apa puternic acida pentru neutralizarea careia se utilizeaza reactivi bazici;

- In rezervorul 2 soseste o apa puternic bazica pentru neutralizarea careia se utilizeaza reactivi acizi;

- In rezervorul final 3 se asigura "neutralizarea finala" cu ambele tipuri de reactivi.

Dozarea reactivilor catre rezervoare este asigurata prin robinetii de reglare RR1, RR2, RR31 si RR32 comandate in tensiune (continual sau bipozitional). Golirea rezervorului se asigura printr-un sistem de sifonare cu prea-plin; la depasirea unui nivel de avarie hmax , este pornita si o pompa suplimentara de golire (nu este ilustrat in figura pentru a nu incarca figura) si dupa caz, se inchide accesul apelor primare catre rezervoare. Neutralizarea apei reziduale (acida, bazica) - rezultata dintrun proces tehnologic (de exemplu de galvanizare) - are loc in 2 (eventual 3) etape:

- neutralizarea preliminara, in rezervoarele 1 si 2; pH - ul la golirea din aceste rezervoare este adus cat mai aproape de valoarea neutrala (pH = 7

- neutralizarea finala, in rezervorul 3 (eventual intr-un al 4-lea, 5-lea rezervor).

Controlul calitatii apelor care ies din rezervoare este asigurat de pH-metrele pH-1, pH-2, pH-3. ma1, ma2, ma3 - sunt motoare de antrenare a sistemelor de amestecare (omogenizare) mecanica.

Descompunerea pe subsisteme a procesului de neutralizare este prezentata in fig. 3.5-16. Serviciile auxiliare sunt asigurate de amestecatoarele mecanice, sistemele de supraveghere a reactivilor s.a..

G. Sistem transportor cu conveior. Structura principala a unui sistem transportor cu conveior este prezentata in fig. 3.5-17 (a). De alungul conturului desfasurat al benzii transportoare, fig.3.5-17 (b) sunt amplasate statiile de lucru aferente procesului tehnologic principal:

- statia (punctul) de incarcare cu "produse de prelucrat" a conveiorului. ST-i,

- punctele de lucru P1, P2, . , P-m amplasate echidistant sau nu, in raport cu distanta dintre doua agatatoare a-i i=1,n

- statia (punctul) de descarcare de pe conveior a "produselor prelucrate".

Exista numeroase moduri de efectuare a transportului cu conveioare:

- cu deplasare continua, fara oprire (de exemplu in abatoarele moderne, unde se prelucreaza porcii sacrificati),

- cu deplasare intermitenta (mers-stationare); pe perioada stationarii are loc prelucrarea locala a produsului (de exemplu asamblarea unor echipamente electronice).

In cazul de fata se presupune ca conveiorul se deplaseaza cu viteza v = const., oprind dupa fiecare pas (egal cu distanta dintre doua puncte de lucru succesive) si stationand un interval de timp constant ts egal cu timpul de prelucrare a piesei la fiecare post de lucru (dimensionarea sarcinilor pe post de lucru asigurand acest timp). Sarcinile de prelucrare pe fiecare post de lucru sunt astfel dimensionate incat sa fie egale: