MODELUL MATEMATIC AL MASINII DE CURENT CONTINUU CU EXCITATIE INDEPENDENTA

MODELUL MATEMATIC AL MASINII DE CURENT CONTINUU CU EXCITATIE INDEPENDENTA

Masina de curent continuu cu excitatie independenta (realizata fie cu magneti permanenti, fie cu ajutorul unei infasurari plasata pe armatura exterioara - stator) este caracterizata in regim dinamic de setul de ecuatii 3.1. Acestea au loc in conditiile considerarii urmatoarelor ipoteze de lucru:

circuite magnetice lineare;

parametrii constanti;

caderea de tensiune la perii neglijabila;

flux de excitatie constant.

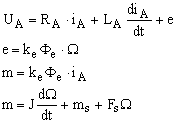(3.1)

unde U_A tensiunea de alimentare;

i_A curentul prin indusul masinii de curent continuu;

Ω = viteza unghiulara a masinii de curent continuu;

R_A = rezistenta indusului;

L_A = inductivitatea proprie a indusului masinii;

e = tensiunea electromotoare indusa;

m = cuplul electromagnetic dezvoltat de masina;

J = momentul de inertie total ( motor + sarcina ) raportat la axul masinii;

m_s = cuplul de sarcina;

F_s = coeficientul total de frecari vascoase;

F_sΩ = cuplul de frecari vascoase;

k_eΦ_e = constanta ce depinde de parametrii constructivi ai masinii de curent continuu.

Pentru a simplifica putin prezentarea vom considera mai departe pentru cuplul de frecari vascoase o valoare mult mai mica decat cea corespunzatoare cuplului de sarcina, care este si cazul celor mai multe sisteme de actionari electrice cu aceasta stuctura. Astfel, ultimul termen din ecuatia cuplului (relatiile 3.1) nu va mai apare.

Sistemul de ecuatii este, in ipotezele mentionate, un sistem linear de ecuatii diferentiale de ordinul intai. Prin aplicarea transformatei Laplace in conditii initiale presupuse nenule (pentru curent si viteza) se obtine sistemul:

(3.2)

Ecuatiile din sistemul de mai sus reprezinta modelul matematic al masinii de curent continuu. Acestor ecuatii le corespunde schema bloc din Fig. 3.2, unde:

constanta de timp electrica a masinii;

constanta de timp electromecanica.

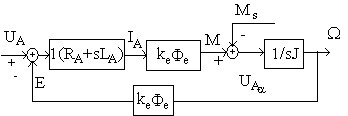
Fig. 3.2. Schema bloc a unei

masini de curent continuu cu excitatie independenta.

Rigiditatea caracteristicii mecanice a unei masini de curent continuu cu excitatie independenta (sau derivatie) este de aproximativ 2 ÷ 5 %. Astfel, datorita acestui aspect variatia vitezei masinii de la functionarea in gol la functionarea in sarcina nominala este foarte mica. Pentru un prim calcul se poate neglija prezenta cuplului de sarcina.

Neglijarea cuplului de sarcina nu va influenta calculele ce vor fi facute in continuare pentru alegerea traductoarelor si respectiv pentru acordarea regulatoarelor de curent si de viteza. Dupa ce toate calculele vor fi facute si se va realiza implementarea regulatoarelor si a filtrelor din cadrul sistemului proiectat, la punerea efectiva in functiune a aplicatiei, in prezenta cuplului de sarcina real, se vor putea face corecturile si reglarile necesare functionarii sistemului cu ajutorul semireglabilelor prevazute in schema de comanda.

Tinand cont de aspectele prezentate anterior, schema bloc a masinii de curent continuu cu excitatie independenta prezentata in Fig. 3.2 va inlocui dreptunghiul cu linie punctata din Fig. 3.1 cu:

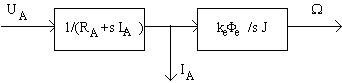
Fig. 3.3. Schema bloc simplificata a unei masini de curent continuu cu excitatie independenta.

Prin utilizarea relatiilor 3.3 pentru schema bloc din Fig. 3.3, schema sistemului de comanda si reglare devine:

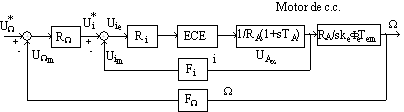
Fig. 3.4. Schema bloc echivalenta a sistemului de comanda si reglare.

unde: ECE element de comanda si executie.

Pentru masina de curent continuu cu excitatie independenta considerata vom avea:

(3.4)

Ω(s)

Datorita prezentei inductivitatii de netezire din circuitul indusului masinii de curent continuu cu excitatie independenta, constantele din relatiile 3.4 se vor calcula cu ajutorul urmatoarelor expresii:

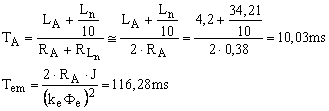(3.5)