Circuit cu rezistor si bobina (RL)

Circuit cu rezistor si bobina (RL)

Pentru analiza circuitului se foloseste montajul din figura 14.6. Prin trecerea comutatorului k in pozitia 1, la momentul initial t=0, intensitatea curentului incepe sa creasca de la valoarea 0 la valoarea maxima I0=E/R.

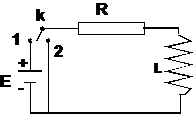
Figura 14.6

Datorita fenomenului de inductie electromagnetica, intensitatea curentului este variabila si dI/dt>0, deci intensitata creste. Prin autoinductie in bobina apare tensiunea electromotoare:

Scriind legea a doua a lui Kirchhoff pentru acest circuit se obtine:

(14.18)

Dupa separarea variabilelor se obtine:

Prin integrare intre t=0 (cand I=0) si t rezulta:

de unde

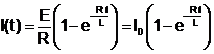(14.19)

In figura (14.7) este prezentata variatia cuentului in functie de timp, conform relatiei (14.19). Se constata ca intensitatea curentului nu ajunge instantaneu la valoarea maxima, ci creste exponential.

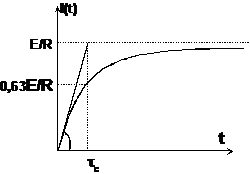
Figura 14.7

Viteza de crestere a curentului este si ea functie de timp si are forma

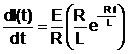
Valoarea initiala a acestei viteze

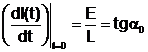(14.20)

este egala cu panta tangentei la curba in origine. Integrand (14.20) intre momentele t=0 si t se obtine ecuatia dreptei:

(14.21)

din care se constata ca daca viteza de crestere a intensitatii curentului ar fi constanta si egala cu viteza initiala, atunci curentul ar atinge valoarea maxima in timpul . Acest timp se numeste constanta de timp a circuitului RL. Valoarea curentului dupa scurgerea unui interval de timp egal cu constanta circuitului este:

Constanta de timp a circuitului reprezinta deci timpul dupa care intensitatea curentului ajunge la valoarea 0,63 din valoarea maxima.

La trecerea comutatorului k in pozitia 2, presupunand ca acesta a stat in pozitia 1 suficient de mult timp pentru ca curentul sa atinga valoarea stationara, sursa va fi decuplata si ecuatia circuitului devine:

(14.22)

Alegand t=0 in momentul in care intensitatea are valoarea I₀=E/R si integrand ecuatia de la t=0 la t, se obtine:

(14.23)

Graficul acestei functii este reprezentat in figura 14.8. Viteza de scadere a intensitatii curentului in circuit va fi:

si are o valoare negativa, deoarece I este pozitiv. Valoarea maxima se obtine pentru t=0

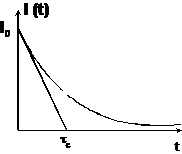
Figura 14.8

si este egala cu panta tangentei in origine la curba. :

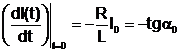(14.24)

Prin integrarea ecuatiei (14.24) intre t=0 si t se obtine ecuatia tangentei la curba in origine:

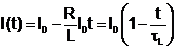(14.25)

Prezenta bobinei in circuit face ca intensitatea sa nu treaca instantaneu in zero in momentul decuplarii sursei. In timpul descarcarii bobinei, energia inmagazinata in campul magnetic al bobinei este disipata sub forma de caldura.

Atunci cand intr-un circuit electric ce contine o bobina se stabileste un curent electric o parte din energia furnizata de sursa este pierduta prin efect Joule iar o parte este inmagazinata in campul magnetic din bobina. Intr-adevar, inmultind cu I fiecare termen al egalitatii (14.22) se obtine:

(14.26)

Membrul stang al egalitatii reprezinta viteza cu care sursa furnizeaza energie circuitului. Primul termen din membrul drept reprezinta puterea Joule disipata pe rezistor, iar al doilea reprezinta viteza cu care energia este acumulata in bobina. Daca este energia campului magnetic din bobina atunci:

(14.27)

Prin integrarea relatiei (14.27) se obtine expresia energiei inmagazinate in solenoid:

(14.28)

Cum pentru un solenoid si , aceasta energie poate fi pusa fub forma:

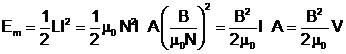(14.29)

unde este volumul cuprins in interiorul bobinei.

Densitatea energiei campului magnetic uniform se poate obtine impartind energia inmagazinata in bobina la volumul bobine:

(14.30)