Circuit cu bobina si condensator

Circuit cu bobina si condensator

Se considera circuitul din figura 14.9 in care bobina este considerata ideala (fara rezistenta). Prin punerea comutatorului k in pozitia 1, condensatorul se incarca de la sursa cu tensiunea E, cu sarcina Q₀=CE. Energia inmagazinata in condensator este .

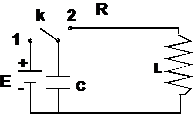
Figura 14.9

Trecand comutatorul in pozitia 2, condensatorul incepe sa se descarce prin bobina. Toata energia pierduta de condensator este inmagazinata in bobina deoarece nu exista pierderi Joule. Atunci cand condesatorul este complet descarcat, intensitatea curentului in bobina are valoarea maxima si energia acumulata in bobina are expresia ½ LI₀². Legea conservarii energiei cere ca:

(14.31)

Mai mult, in orice moment trebuie sa existe egalitatea:

(14.32)

Dupa ce condensatorul s-a descarcat complet, sensul curentului din circuit se schimba si energia acumulata in campul magnetic al bobinei trece din nou in energie electrica acumulata in condensator.

In desfasurarea procesului descris anterior sarcina electrica a condensatorului si intensitatea curentului electric prin bobina oscileaza. Oscilatiile descrise sunt oscilatii electromagnetice. Intr-adevar, considerand un moment de timp in cursul descarcarii condensatorului, cand sarcina acestuia este Q si curentul prin bobina I, este evident ca I=dQ/dt. Scriind legea a doua a lui Kirchhoff pentru acest circuit se obtine:

(14.33)

unde este pulsatia proprie a circuitului LC. Ecuatia caracteristica corespunzatoare este:

(14.34)

si are solutiile . Solutia generala a ecuatiei (14.33) va fi:

(14.35)

unde C₁ si C₂ sunt constante complexe.

Cum sarcina electrica este o marime reala, rezulta ca si deci:

(14.36)

ecuatie satisfacuta daca si evident . Acestea pot fi alese sub forma:

(14.37)

Inlocuind (14.37) in (14.35) se obtine:

(14.38)

unde A si  sunt constante. Semnificatia fizica si valoarile acestora se pot determina din conditiile initiale ale problemei: la t=0, Q(0)=0 si . Se obtine A=Q₀ si =0, deci

(14.39)

Se pot exprima si caderea de tensiune la bornele condensatorului si intensitatea curentului prin circuit:

Se constata ca intensitatea maxima se realizeaza atunci cand sarcina condensatorului este nula. Q(t) si U(t) oscileaza in faza, iar I(t) este in intarziere cu /2.

14.4. Circuit RLC

Circuitul este cel din figura 14.9 in care bobina este considerata cu rezistenta R_L. Pentru acest circuit se poate scrie:

(14.40)

si cum , se obtine:

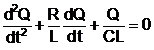(14.41)

Introducand notatiile , ecuatia (14.41) devine

(14.42)

Ecuatia diferentiala (14.42) are ecuatia caracteristica:

cu solutiile

La valori mici ale rezistentei circuitului, si expresia de sub radical devine negativa, radacinile capata forma iar forma generala a solutiei ecuatiei (14.42) este:

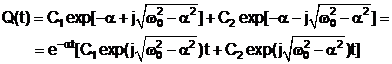(14.43)

Expresia (14.43) poate fi pusa sub forma:

(14.44)

Relatia (14.44) descrie oscilatii amortizate de pulsatie inferioara valorii ₀.

Viteza de disipare a energiei in circuitele electrice se poate caracteriza prin decrementul logaritmic al amortizarii :

unde se numeste factor de calitate al circuitului si T este perioada oscilatiilor electrice. Se poate arata ca factorul de calitate este numeric egal cu raportul dintre energia electrica existenta in circuit la momentul t si energia disipata in circuit in perioada T imediat urmatoare, inmultit cu 2.

Daca amortizarea este puternica, si este real. Solutia capata forma:

unde C₁ si C₂ sunt reale. Scaderea este exponentiala, fara caracter oscilatoriu.

Trecerea de la regimul amortizat la descresterea exponentiala are loc pentru , deci , unde R_cr se numeste rezistenta critica.