 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
EXEMPLE REZOLVATE SI ANALIZATE APLICAND TEHNICA ANOVA
Exemplul1
Intr-un studiu de psihologia muncii , un cercetator a dorit sa determine influenta a trei programe de reinsertie profesionala asupra procesului de re-angajare, subiectii fiind persoane licentiate in stiinte economice. In acest sens , au foat selectati aleator cate un numar de 20 subiecti care sa participe la fiecare din cele trei programe . Somerii provin din toate sectoarele de activitate (public si privat) si au fost integrati in unul din programele de reabilitare.In vederea evaluarii eficientei programului s-a masurat perioada de timp de somaj exprimata in saptamani necesara fiecaruia pentru a-si gasi un alt loc de munca.
|
Program1 |
Program2 |
Program3 |
|
1 |
8 |
1 |
|
3 |
7 |
3 |
|
5 |
5 |
4 |
|
4 |
6 |
2 |
|
7 |
9 |
6 |
|
6 |
7 |
3 |
|
7 |
2 |
5 |
|
8 |
7 |
1 |
|
4 |
9 |
7 |
|
5 |
8 |
5 |
|
4 |
7 |
1 |
|
2 |
9 |
3 |
|
6 |
5 |
5 |
|
7 |
7 |
2 |
|
8 |
9 |
6 |
|
4 |
7 |
7 |
|
1 |
2 |
8 |
|
3 |
7 |
4 |
|
5 |
9 |
1 |
|
6 |
9 |
3 |
|
7 |
7 |
5 |
Pasul 1
Identificarea variabilelor
Analizand problema anterioara identificam ca variabila independenta:
A - programul de reinsertie, cu cele trei modalitati
a1 - programul 1
a2 - programul 2
a3 - programul 3
si variabila dependenta X - eficienta programului de reinsertie operationalizata prin numarul de saptamani necesare fiecarei persoane pentru a-si gasi un loc de munca.
Pasul 2
Designul cercetarii
Avem un design experimental de baza cu o variabila independenta cu k modalitati, inter subiect deoarece la fiecare program au participat alti subiecti.
|
A |
a1 |
a2 |
a3 |
|
X |
|
|
|
Pasul 3
Ipoteza
Programul de reinsertie profesionala la care participa persoana difera semnificativ din punct de vedere al eficientei.
Sau
Exista diferente semnificative intre perioada de timp necesara reinsertiei profesionale a persoanelor participante la training in functie de tipul programului urmat.
Pasul 4
Constructia bazei de date si alegerea metodei statistice
Pentru a construi baza de date ne punem intrebarea
"Ce stim despre fiecare subiect?"
In cazul nostru, stim la ce program de reinsertie a participat fiecare si numarul de saptamani necesar pentru a-si gasi un loc de munca (eficienta programului). In consecinta, in baza de date vom avea doua variabile, tipprogra cu trei modalitati si persomaj = perioada de somaj.
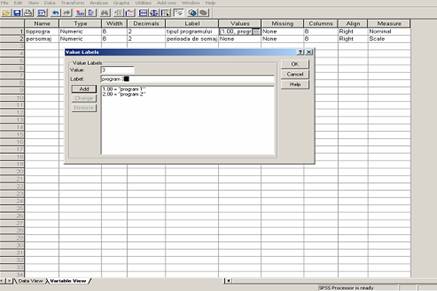
Pentru a decide cu privire la metoda de analiza statistica adoptata va trebui sa verificam forma distributiei datelor.
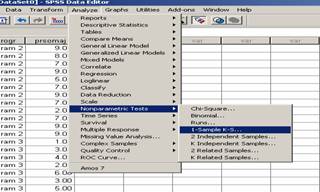
Daca datele prezinta o distributie normala la nivelul populatiei atunci vom utiliza metoda inferentiale parametrice - respectiv ANOVA cu un singur factor intergrup (One Way Anova), iar daca asumtia cu privire la normalitatea distributiei nu este indeplinita vom folosi metode inferentiale nonparametrice, respectiv testul U generalizat denumit si Kruskal - Walis sau proba medianei extinsa - optiunea depinzand de particularitatile datelor.
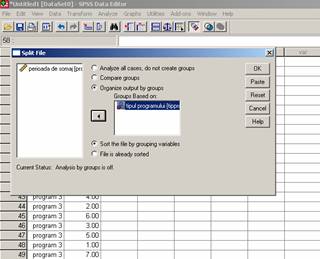
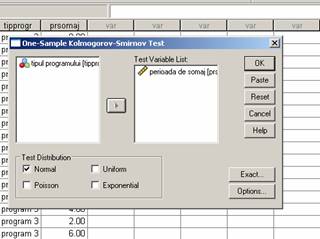
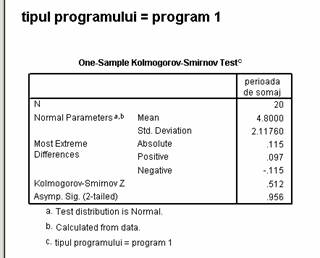
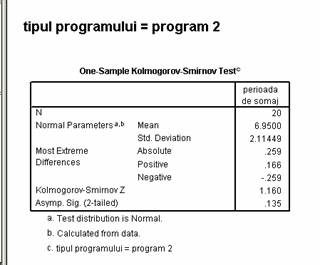

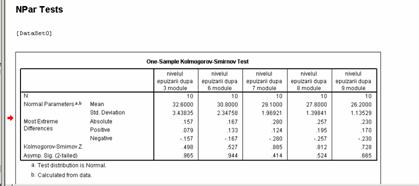
In vederea verificarii formei distributiei vom utiliza testul non-parametric Kolmogorov - Smirnov pe fiecare esantion ce urmeaza a fi comparat.
In acest sens vom selecta functia de SPLIT FILE din meniul DATA si vom cere organizarea output-ului in functie de modalitatile variabilei independente ( adica a tipului de program) asa cum apare in ecranele de mai sus.
Analizand valorile testului Kolmogorov - Smirnov in toate cele 3 conditii ale variabilei program, constatam ca datele respecta criteriul de normalitate la nivelul populatiei din care fac parte.
In consecinta vom utiliza metode de analiza parametrice si anume ANOVA cu un singur factor intergrup (One Way Anova).
Pasul 5
Analiza statistica propriu - zisa
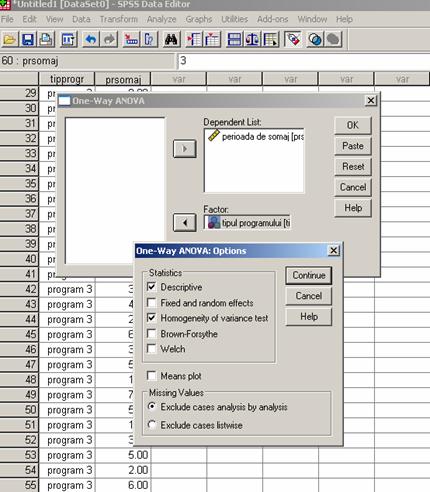
Variabila
Dependenta
Variabila
independenta
![]()
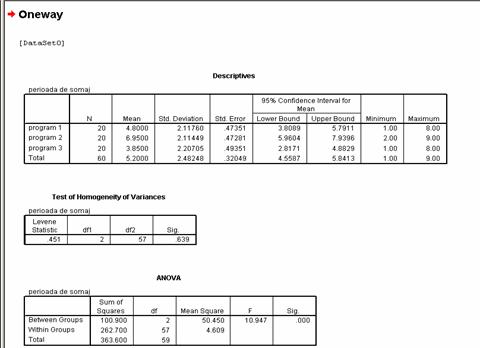 Analiza statistica descriptiva
releva existenta unor diferente intre mediile timpilor necesari
reinsertiei profesionale a personalului cuprins in programele de
reinsertie in functie de tipul programului. Vom analiza in continuare
in ce masura aceste diferente intre medii se datoreaza
hazardului sau sunt efectul programelor de reinsertie la care
participa persoana.
Analiza statistica descriptiva
releva existenta unor diferente intre mediile timpilor necesari
reinsertiei profesionale a personalului cuprins in programele de
reinsertie in functie de tipul programului. Vom analiza in continuare
in ce masura aceste diferente intre medii se datoreaza
hazardului sau sunt efectul programelor de reinsertie la care
participa persoana.
![]() Testul de omogenitateLevene ne arata in ce
masura esantioanele comparate sunt omogene din punct de vedere
al variantei, in cazul de fata Levene = .451 si p = .639
> pragul critic p = .05ceea ce ne permite sa afirmam ca cele
trei esantioane comparate sunt omogene din punct de vedere al
variantei.
Testul de omogenitateLevene ne arata in ce
masura esantioanele comparate sunt omogene din punct de vedere
al variantei, in cazul de fata Levene = .451 si p = .639
> pragul critic p = .05ceea ce ne permite sa afirmam ca cele
trei esantioane comparate sunt omogene din punct de vedere al
variantei.
Sa nu uitam ca omogenitateavariantei esantioanelor comparate este o conditie necesara pentru analiza de varianta.
Pasul 6
Interpretarea rezultatelor
Analizand in continuare relatia dintre timpul necesar reinsertiei profesionale ( tabelul ANOVA) si tipul de program la care persoana participa, detinem un F (2, 57) = 10.947 si un p = .000 < p critic = .01 deci putem afirma cu un risc de a gresi de 1% ca perioada de timp necesara reinsertiei profesionale a persoanelor aflate in somaj difera in functie de programul la care participa.
Testul F omnibus fiind un test global nu ne permite sa vedem intre care dintre cele 3 programe exista diferente, in consecinta vom apela la probe post - hoc.
In cazul nostru fiind vorba de dispersii egale si numar egal de subiecti putem opta pentru Scheffe sau Tukey. Cum insa Scheffe este un test statistic mai puternic prima noastra optiune va fi pentru acesta.
![]()
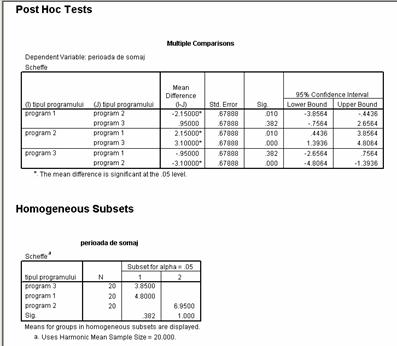
Analizand rezultatele testelor post - hoc constatam ca diferenta mediilor dintre timpii necesari reinsertiei profesionale in cazul participarii la programul 1 de formare, comparativ cu participantii la programul 2 este de - 2.15 semnificativ la un p = .01 < pragul critic de .05, ceea ce ne permite sa afirmam cu un risc de a gresi mai mic de 2 % ca subiectii participanti la programul 2 au nevoie de un timp mai mare pentru a-si gasi un loc de munca comparativ cu cei care participa la programul 1, cu aproximativ 2 saptamani ( in medie).
Comparand rezultatele persoanelor implicate in programul 2 comparativ cu cei implicati in programul 3, diferentele mediilor sunt de 3.10 si p = .0001.
Putem afirma cu un risc de a fresi mai mic de 1 % ca subiectii participanti la programul 2 au nevoie de un timp mai lung - in medie cu 3.1 saptamani - comparativ cu subiectii participanti la programul 3 pentru a-si gasi un loc de munca.
Sintetizand, putem afirma ca programul 2 este cel mai putin eficient, el diferind semnificativ atat de programul 1 cat si de programul 3, motiv pentru care in cazul replicarii acestei interventii la acest program am fi indreptatiti sa renuntam fiind cel mai putin eficient.
Exemplul 2
Managerul spitalului de urgenta X, interesat fiind de problemele cu care se confruna personalul medical mediu solicita un studiu organizational care releva existenta unui nivel ridicat al epuizarii. Ca urmare se propune implementarea unui program de interventie structurat pe 9 module. Deoarece directorul nu este convins de necesitatea acestui numar mare de module, el solicita realizarea unor evaluari post -interventie dupa primele 3 modul, dupa primele 6 module si apoi dupa fiecare nodul in parte.
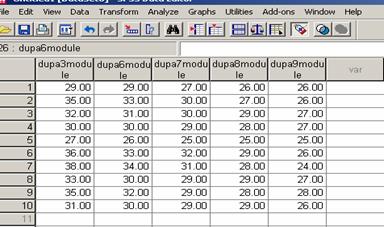
|
Subiect |
Dupa 3 module |
Dupa 6 module |
Dupa 7 module |
Dupa 8 module |
Dupa 9 module |
|
1 |
29 |
29 |
27 |
26 |
26 |
|
2 |
35 |
33 |
30 |
27 |
26 |
|
3 |
32 |
31 |
30 |
29 |
27 |
|
4 |
30 |
30 |
29 |
28 |
27 |
|
5 |
27 |
26 |
25 |
25 |
25 |
|
6 |
36 |
33 |
32 |
29 |
26 |
|
7 |
38 |
34 |
31 |
28 |
24 |
|
8 |
33 |
30 |
29 |
29 |
27 |
|
9 |
35 |
32 |
29 |
28 |
28 |
|
10 |
31 |
30 |
29 |
29 |
26 |
|
11 |
30 |
30 |
27 |
27 |
24 |
Pasul 1
Identificarea variabilelor
In studiul prezentat anterior avem o singura variabila independenta
A - durata programului de interventie:
a1 - 3 module
a2 - 6 module
a3 - 7 module
a4 - 8 module
a5 - 9 module
si o variabila dependenta X - nivelul epuizarii.
Pasul 2
Formularea ipotezei
Ipoteza de cercetare
Nivelul epuizarii personalului medical este influentat de durata programului de trening.
Sau
Exista diferente semnificative in nivelul epuizarii personalului medical in functie de durata programului de training.
Ipoteza nula
Nivelul epuizarii personalului medical nu difera in functie de durata programului de training.
μ3module =μ6 module = μ7 module = μ8 module = μ9 module
Pasul 3
Tipul de design
Vom avea un design experimental de baza intragrup (fiind vorba de aceeasi subiecti, in diverse momente) cu k modalitati ale variabilei independente ( 5 in particular in cazul nostru), adica: dupa 3 module, dupa 6 module¸ dupa 7 module, dupa 8 module, dupa 9 module.
Pasul 4
Elaborarea bazei de date si alegerea metodei statistice
Pentru a elabora baza de date ne punem intrebarea:
"Ce stim despre fiecare subiect?"
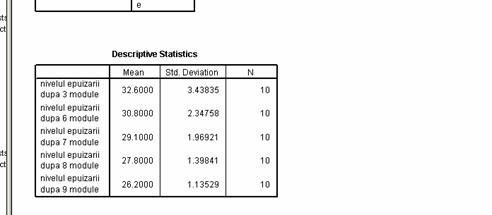
Incercand sa raspundem constatam ca noi cunoastem nivelul epuizarii persoanei dupa 3 module, nivelul epuizarii persoanei dupa 6 module, nivelul epuizarii persoanei dupa 7 module, nivelul epuizarii persoanei dupa 8 module, nivelul epuizarii persoanei dupa 9 module, deci pentru fiecare persoana cunoastem cate 5 nivele ale epuizarii.
Cum toate informatiile pe care le stim despre o persoana se vor gasi pe o linie in baza de date inseamna ca vom avea 5 coloane in baza de date corespunzatoare celor 5 nivele ale epuizarii pe care le cunoastem.
Etapa urmatoare va fi sa verificam forma distributiei datelor pentru a putea opta in cunostinta de cauza pentru o metoda de analiza statistica, parametrica in cazul nostru, in care distributia esantioanelor analizate respecta criteriul de normalitate a distributiei sau pentru o metoda de analiza statistica neparametrica in cazul in care nu tinem cont de forma distributiei.
In toate conditiile in care este posibil vom opta pentru o analiza a datelor parametrica in fata uneia neparametrice, deoarece metodele de analiza statistica parametrica au o finete mult mai mare.
Analizand tabelul testelor Kolmogorov - Smirnov, constatam ca celor 5 nivele ale lui Kolmogorov - Smirnov calculate de noi le corespund praguri de semnificatie intre .414 si .965 deci sunt mai mari decat pragul critic de .05 ceea ce ne permite sa afirmam ca distributiile la nivelul populatiilor din care sunt extrase datele analizate respecta criteriul de normalitate. In consecinta vom putea utiliza metoda de analiza statistica parametrica in cazul nostru, metoda pentru care vom opta va fi ANOVA cu masurari repetate.
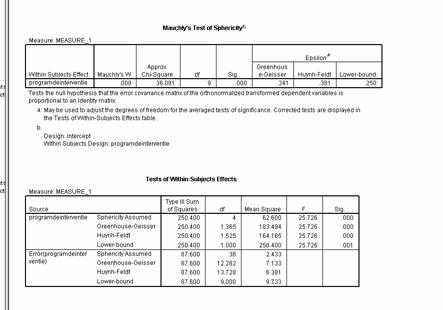
Pasul 5
Analiza datelor
Deoarece este un design cu masurari repetate importanta majora o are analiza sfericitatii datelor oferita de testul Mauchly's. In cazul nostru valoarea testului Mauchly's W = .008 iar p = .000 mai mic decat pragul critic de .05 deci conditia de sfericitate nu este indeplinita. Analizand in continuare aproximarile lui Epsilon constatam ca acestea se situeaza intre [.341, .381] deci mai mici de .75 motiv pentru care vom concluziona ca in continuare vom utiliza in interpretarea valorilor F omnibuz corectia lui Greenhouse - Geisser.
Pasul 6
Interpretarea datelor
In cercetarea intreprinsa obtinem un F (1.36, 12,28) = 15.726 semnificativ la un p = .001 mai mic decat pragul critic de .05 ceea ce ne permite sa spunem ca exista un efect principal semnificativ si la nivelul epuizarii personalului medical este influentat semnificativ de numarul de module la care participa din programul de interventie, aceasta afirmatie riscand sa fie gresita in mai putin de 1%cazuri.
Totusi nu putem spune intre care din cele 5 situatii analizate exista aceste diferente deoarece F omnibuz este un test global. Pentru acuratizarea concluziilor noastre vom folosi testul post - hoc Bonferroni (cel mai recomandat de literatura de specialitate pentru designurile intragrupale).
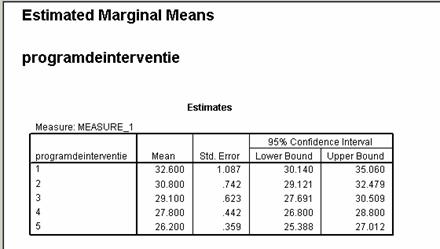
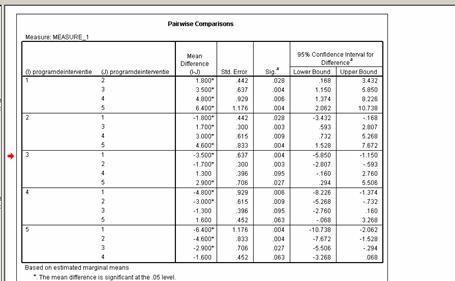
Analizand testele post - hoc Bonferroni prin intermediul mediei diferentelor indica existenta unor diferente semnificative intre primele doua etape adica dupa 3 module si dupa 6 module - cu toate celelalte, si de asemenea exista diferente semnificative intre etapa a treia (dupa 7 module) si etapa a cincia ( dupa 9 module).
Acest lucru ne va permite sa spunem ca recomandarea specialistului in resurse umane a fost intemeiata si ca daca totusi directorul spitalului doreste sa faca o economie reducand investitia prin scurtarea programului de interventie atunci se recomanda a se opri dupa 7 module (adica dupa etapa 3).
Exemplul 3
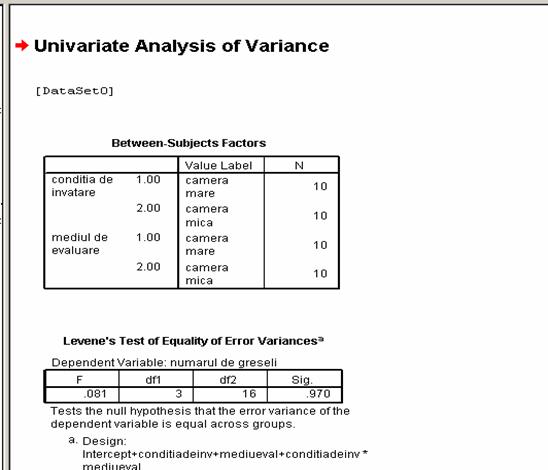
Un specialist isi propune sa verifice efectul mediului de invatare asupra encodarii lingvistice.
Astfel, u fost alesi 40 de subiecti care erau impartiti in doua loturi experimentale: primul lot de subiecti, adica 20, erau pusi sa memoreze o lista de cuvinte intr-o sala mare, iar ceilalti 20 de subiecti erau plasati pentru memorarea listei intr-o sala mica.
Etapa de evaluare a fost realizata in felul urmator: 10 subiecti care au studiat in sala mare trebuiau sa reproduca cuvintele in aceeasi sala, iar ceilalti 10 subiecti care au memorat intr-o sala mare etapa de reproducere s-a desfasurat intr-o sala mica. La fel s-a procedat si cu ceilalti 20 de subiecti care au studiat in sala mica. Pentru reproducere 10 erau plasati intr-o sala mare, iar ceilalti 10 de subiecti intr-o sala mica.
Ideea de la care s-a pornit cercetarea posibilitatea existentei unei diferente semnificative asupra performantelor in reproducerea listei de cuvinte in functie de conditia de invatare si mediul de evaluare.
Mediul de testare
|
|
Sala mare de testare |
Sala mica de testare |
|
Sala mare invatare de |
15 20 11 18 16 |
5 8 1 1 5 |
|
Sala de invatare mica |
1 4 2 5 8 |
22 15 20 17 16 |
Conditia de
invatare
Pasul 1
Stabilirea ipotezelor
Anova bifactorial evalueaza trei ipoteze diferite
Ipoteza specifica 1. Exista diferente semnificative in ceea ce priveste performanta in functie de conditia de invatare (factorul A)
Hs: μA1 ≠ μ A2
Ipoteza nula: Diferente obtinute asupra performantelor a celor doua grupe de subiecti impartiti dupa conditia de invatare se datoreaza hazardului.
H0: μA1 μ A2
Ipoteza specifica 2. Exista diferente semnificative in ceea ce priveste performanta in functie de mediul de testare (factorul B)
Hs: μB1 ≠ μ B2
Ipoteza nula: Diferente obtinute asupra performantelor a celor doua grupe de subiecti impartiti dupa mediul de testare se datoreaza hazardului.
H0: μB1 μ B2
Ipoteza specifica 3. Exista diferente semnificative in ceea ce priveste performanta in functie de interactiunea dintre conditia de invatare si mediul de testare(factorul A X B)
Ipoteza nula: Diferente obtinute asupra performantelor a celor doua grupe de subiecti impartiti dupa conditia de invatare se datoreaza hazardului.
Pasul 2
Stabilirea gradelor de libertate
Valoarea gradelor de libertate trebuie sa le obtinem pentru fiecare dintre cele trei valori F.
Specific, noi avem nevoie de un dfA, dfB si df AXB pentru numarator si dfintra pentru numitor.
dfA = a - 1 = 2 - 1 = 1
dfB = b - 1 = 2-1 = 1
df AXB = (a - 1) (b - 1) = (1)(1)= 1
dfintra = N - ab = 20 - (2)(2) = 20 - 4 = 16
Deci, toate trei F vor avea df = 1, 16. Cu α = .05, valoarea critica pentru F este F = 4.49. Pentru fiecare test, obtinerea valorii F trebuie sa depaseasca aceasta valoare critica pentru a respinge ipoteza nula.
Pasul 3
Analiza datelor
Analiza datelor pentru Anova bifactorial se divide intr-o serie de pasi
1. Calcularea sumelor statistice pentru datele brute. Acestea implica calcule pentru AB total si SS pentru fiecare conditie, gasirea lui A total si B total pe linii si coloane, respectiv, obtinerea lui G si Σx² pentru setul intreg de scoruri.
2. Executati prima scena a analizelor: separati variabilitatea totala (SS si df) in componentele inter si intra.a
3. Executati a doua scena a analizelor: separati variabilitatea inter (SS si df) in efectul A, efectul B si interactiunea componentelor.
4. Calculati mediile patrate pentru rapoartele F.
5. Calculati rapoartele F.
Calculul statisticii sumare
Utilizati formula de calcul pentru a obtine SS pentru fiecare conditie. Aceste calcule vor furniza valori numerice pentru totalul de randuri si coloane (A si B) si de asemenea G si Σx².
![]()
SALA MARE DE TESTARE SALA MICA DE TESTARE
SALA MARE DE INVATARE SALA MARE DE INVATARE
X X² X X².
15 225 5 25
20 400 8 64
11 121 1 1
18 324 1 1
16 256 5 25 .
Σx=80 Σx²= 1326 Σx=20 Σx²=116
SS = Σx² - (Σx²) SS = Σx² - (Σx²)
n n
![]() = 1326 - 80² =
116 - 20²
= 1326 - 80² =
116 - 20²
5 5
= 1326 - 1280 =116 - 80
= 46 = 36
AB = Σx = 80 AB = Σx = 20
![]()
SALA MARE DE TESTARE SALA MICA DE TESTARE
SALA MICA DE INVATARE SALA MICA DE INVATARE
X X² X X².
1 1 22 484
4 16 15 225
2 4 20 400
5 25 17 289
8 64 16 256 .
Σx=20 Σx²= 110 Σx=90 Σx²=1654
SS = Σx² - (Σx²) SS = Σx² - (Σx²)
n n
= 110 - 20 ² = 1654 - 90²
5 5
= 110 - 80 =1654 - 1620
= 30 = 34
AB = Σx = 20 AB = Σx = 90
Totalul pe coloane ( factorul B) este B1 = 100 si B2 = 110. Totalul pe randuri ( factorul A) este A1= 100 si A2 = 110. Totalul general al datelor este G = 210, iar Σx² pentru intregul set se poate obtine adunand valorile Σx² pentru fiecare conditie.
Σx² = 1 326 + 116 + 110 + 1654 = 3 206
Pentru acest studiu, exista doua modalitati pentru factorul A si pentru factorul B, deci a = b = 2, si aici n = 5 scorurile pentru fiecare dintre cele patru conditii, deci N = 20.
Scena 1 a analizelor
Incepem sa analizam SS in doua componente de baza
SS total = Σx² - G² = 3 206 - 210 ² = 3 206 - 2 205 = 1 001
N20
SS inter celule = Σ AB² - G ² = 80² + 20² + 20² + 90² - 210²
n N 5 5 5 5 20
= 1 280 + 80 + 80 + 1 620 - 2 205
= 3 060 - 2 205
= 855
SS intra = ΣSS fiecare celula = 46 + 36 30 + 34 = 146
Pentru a ceasta scena, valoarea df este
df total = N - 1 = 20 - 1 = 19
df intergrup = ab - 1 = 4 - 1 = 3
dfintra = N - ab = 20 - 4 = 16
iScena 2 a analizelor
IncepeM sa calculam SS intragrup
SSA Σ A² - G²
bn N
= 100² + 110 ² - 210 ²
10 10 20
= 1 000 + 1 210 - 2 205
= 5
SSB = Σ B² - G²
an N
= 100² + 110 ² - 210 ²
10 10 20
= 1 000 + 1 210 - 2 205
= 5
SS AXB = SS inter celule - SSA - SSB
= 855 - 5 - 5
= 845
Pentru scena 2 valoarea lui df este
df A = a - 1 = 2 - 1 = 1
df B = b - 1 = 2 - 1 = 1
df AXB = ( a - 1 )(b - 1) = (1)(1) = 1
Calculul MS (mediei patrate)
MS A = SSA = 5 = 5
dfA 1
MS A = SSB = 5 = 5
dfB 1
MS AXB = SSAXB = 845 = 845
dfAXB 1
MS intra = SSintra = 146 = 9.125
dfintra 16
Calcularea raportului F
Pentru factorul A ( conditia de invatare)
F = MS A = 5 = 0.55
MS intra 9. 125
Pentru factorul B ( mediul de testare)
F = MS B = 5 = 0.55
MS intra 9. 125
Pentru interactiunea dintre AXB
F = MS AXB = 845 = 92.60
MS intra 9. 125
Pasul 4
Decizia pentru fiecare H0 si concluziile
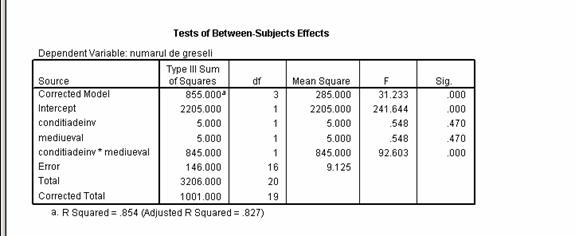
Pentru factorul A, conditia de invatare, am obtinut un raport F, F = 0.55, nu se afla in intervalul critic. In consecinta, sansele ca diferentele sa se datoreze hazardului fiind prea mari nu ne pronunta asupra deciziei. In concluzie, marimea salii de invatare nu are efecte semnificative asupra performantelor, F (1, 16) = 0.55, p > . 05.
Pentru factorul B, mediul de testare, obtinem un raport F, F = 0, 55, nu se afla in intervalul critic. In consecinta, sansele ca diferentele sa se datoreze hazardului fiind prea mari nu ne pronunta asupra deciziei. In concluzie, marimea salii de testare nu are efecte semnificative asupra performantelor, F (1, 16) = 0.55, p > . 05.
Pentru interactiunea AXB, obtinem un raport F, F = 92.60, depaseste valoarea critica a lui F = 4.46. In consecinta, respingem ipoteza nula. In concluzie, interactiunea dintre marimea salii de invatare si marimea salii de testare are efecte semnificative asupra performantelor, F (1, 16) = 92.60, p > . 05.
Observati ca interactiunea dintre medii este semnificativa deci trebuie sa fiti precauti a interpreta efectul mediilor. In acest experiment, de exemplu, marimea salii de testare ( factorul B) nu are efect asupra performantelor, depinzand si in care sala a fost realizata lectura. Specific, performanta este mai ridicata cand testarea se realizeaza in aceeasi sala unde a fost lecturarea, iar performanta este mai scazuta cand lecturarea si testarea se realizeaza in camere diferite.
Urmatorul tabel rezuma rezultatele analizelor
|
Sursa |
SS |
df |
MS |
F |
|
Intergrup |
855 |
3 |
|
|
|
A ( sala de lectura) |
5 |
1 |
5 |
F = 0.55 |
|
B (sala de testare) |
5 |
1 |
5 |
F = 0.55 |
|
Interactiunea dintre AXB |
845 |
1 |
845 |
|
|
Intragrup |
146 |
16 |
9.125 |
F = 92.60 |
|
Total |
1 001 |
19 |
|
|
Exemplul 4
Un psiholog educational studiaza motivatia elevilor.Un lot de 7 subiecti sunt urmariti timp de 3 ani din clasa a patra pana in clasa a sasea.In fiecare an elevii conpleteaza un chestionarv masurind motivatia si entuziasmul pentru scoala centrat pe 3 discipline: matematica, romana, muzica.Psihologul vrea sa stie daca apar schimbari semnificative intre nivelurile de motivatie de-a lungul celor 3 ani si intre interesul pentru diferite discipline.
|
matematica |
romana |
muzica |
|
||||||
|
Clasa IV |
Clasa V |
Clasa VI |
Clasa IV |
Clasa V |
Clasa VI |
Clasa IV |
Clasa V |
Clasa VI |
|
|
23 |
19 |
22 |
25 |
20 |
22 |
26 |
24 |
25 |
|
|
19 |
19 |
20 |
19 |
20 |
21 |
24 |
21 |
23 |
|
|
21 |
20 |
20 |
23 |
21 |
22 |
25 |
24 |
24 |
|
|
24 |
19 |
22 |
25 |
22 |
22 |
26 |
23 |
25 |
|
|
23 |
21 |
21 |
20 |
20 |
21 |
21 |
21 |
21 |
|
|
24 |
21 |
21 |
21 |
20 |
20 |
22 |
21 |
21 |
|
|
21 |
18 |
20 |
20 |
19 |
20 |
19 |
18 |
20 |
|
In cercetarea de mai sus identificam doua variabile independente:
A - disciplina, cu trei modalitati
a1- matematica
a2 - romana
a3 - muzica
Din punct de vedere al acestei variabile (discipline) avem un design intrasubiect.
B - momentul evaluarii
b1 - clasa a IV-a
b2 - clasa a V-a
b3 - clasa a VI -a
Si din punct de vedere al variabilei B designul este intrasubiect.
Variabila dependenta este X - interesul pentru studiu, operationalizat prin nivelul motivarii subiectului pentru din disciplinele evaluate.
Ipotezele cercetarii sunt:
Ipoteza 1: (pentru varianta A)
Interesul pentru studiu al elevilor difera in functie de materie, in sensul ca materiile mai apropiate de aptitudinile personale prezinta un interes mai ridicat.
Sau
Exista diferente semnificative in interesul pentru studiu al elevilor in functie de materie.
Ipoteza 2: (pentru varianta B)
Interesul pentru studiu al elevilor difera in functie de etapa de dezvoltare in care se situaeaza.
Sau
Exista diferente semnificative in interesul pentru studiu al elevilor in functie de varsta acestora.
Ipoteza 3: (pentru interactiunea AXB)
Interesul pentru studiu al elevilor este influentat de interactiunea dintre materie si etapa de dezvoltare in care se afla elevul.
Sau
Exista diferente semnificative in interesul pentru studiu al elevilor in functie de interactiunea dintre materia analizata si varsta acestuia.
Putem deci concluziona ca avem un design de cercetare bifactorial intrasubiect.
|
|
a1 |
a2 |
a3 |
|
b1 |
|
|
|
|
b2 |
|
|
|
|
b3 |
|
|
|
Design 3X3 bifactorial in care avem doua variabile independente A si B - deci doua efecte principale, cate unul pentru fiecare dintre ele, si interactiunea acestora AXB.
Pornind de la aceste date ale problemei vom face o analiza sumara pentru a vedea daca exista anumite diferente intre mediile rezultatelor subiectilor in cele 9 situatii analizate (3X3 = 9).
Pentru a face o analiza preliminara a posibilelor efecte vom calcula mediile motivarii subiectilor in fiecare conditie experimentala.
|
|
a1 matematica |
a2 romana |
a3 muzica |
|
|
b1 clasa a IV-a |
22.14 |
21.85 |
23.28 |
B1 = 22.42 |
|
b2 clasa a V-a |
19.57 |
20.28 |
21.71 |
B2 = 20.52 |
|
b3 clasa a VI-a |
20.85 |
21.14 |
22.71 |
B3 = 21.56 |
|
|
A1 = 20.85 |
A2 = 21.09 |
A3 = 22.56 |
|
A1 ≠ A2 ≠ A3 => este posibil ca variabila A sa aiba efect.
B1 ≠ B2 ≠ B3 => este posibil ca variabila B sa aiba efect.
Reprezentand grafic datele observam ca liniile nu se intersecteaza deci nu exista suspiciune de interactiune.
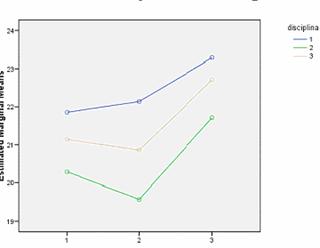
In continuare vom rezolva problema cu ajutorul programului SSPS 15.0.
Pentru aceasta prima etapa o constituie construirea bazei de date.
Pentru ca sa ne fie mai usor si ca sa nu gresim intrebarea pe care o vom pune este:
"Ce stim despre fiecare subiect?"
analizand textul problemei constatam ca stim pentru fiecare subiect urmatoarele:
1. motivatia pentru romana in clasa a IV-a
2. motivatia pentru romana in clasa a V-a
3. motivatia pentru romana in clasa a VI-a
4. motivatia pentru matematica in clasa a IV-a
5. motivatia pentru matematica in clasa aV-a
6. motivatia pentru matematica in clasa a VI-a
7. motivatia pentru muzica in clasa a IV-a
8. motivatia pentru muzica in clasa a V-a
9. motivatia pentru muzica in clasa a VI-a.
In consecinta vom avea 9 coloane in baza de date corespondente pentru cele 9 aspecte pe care le cunoastem despre fiecare subiect.
Baza de date va arata astfel in fereastra Variable View
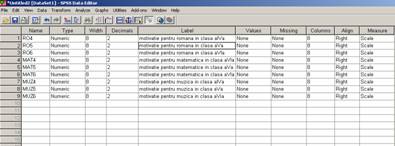
Iar daca ne uitam in fereastra Data View baza noastra de date va arata astfel:
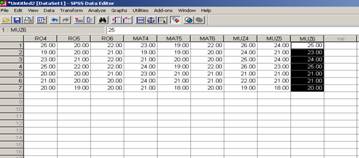
Pasul urmator va fi sa analizam forma distributiei pentru a putea decide cu privire la testul statistic utilizat. In acest sens vom folosi testul non-parametric Kolmogorov - Smirnov pentru a verifica forma distributiei datelor.
Analizans tabelul de mai jos constatam ca pentru toate situatiile analizate valorile K - S obtinute le corespund praguri de semnificatie p > .05 ceea ce ne permite sa spunem ca la nivelul populatiei distributiile motivatiei elevilor la romana, matematica si muzica in etapele de varsta studiate ( clasa a IV-a, clasa a V-a, clasa a VI-a) respecta criteriul de normalitate.

![]()
![]()
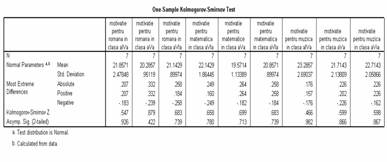
valoarea K-S pragul de
calculata semnificatie
Tinand cont de normalitatea distributiei datelor si de faptul ca efectivele fiecarui esantion analizat este > 5 decidem ca putem utiliza metoda de comparatie parametrica si anume ANOVA bifactorial intragrup (aceasta din urma fiind dictata de tipul de esantioane analizate).
Fiecare din cele doua variabile implicate este o variabila intra - subiect, in consecinta pentru fiecare dintre ele vom defini cate un factor.

![]()
![]()
![]()
factorul B - clasa numarul de modalitati
(momentul evaluarii) ale factorului B

stabilirea corespondenta
(2,2) inseamna ca ne intereseaza valoarea variabilei dependente corespondente variabilei a2b2, deci motivatia elevilor pentru matematica in clasa a V-a.
Pentru a ne usura munca si a evita erorile in stabilirea corespondentelor se recomanda a intocmi tebelul de corespondente intre:
Conditie experimentala Variabila dependenta
corespondent acesteia
(1,1) - a1b1 - motivatie pentru romana in clasa aIV-a
(1,2) - a1b2 - motivatie pentru romana in clasa aV-a
(1,3) - a1b3 - motivatie pentru romana in clasa aVI-a
(2,1) - a2b1 - motivatie pentru matematica in clasa aIV-a
(2,2) - a2b2 - motivatie pentru matematica in clasa aV-a
(2,3) - a2b3 - motivatie pentru matematica in clasa aVI-a
(3,1) - a3b1 - motivatie pentru muzica in clasa aIV-a
(3,2) - a3b2 - motivatie pentru muzica in clasa aV-a
(3,3) - a3b3 - motivatie pentru muzica in clasa aVI-a.
Dupa ce am stabilit corespondentele intram la OPTIONS pentru a seta statisticile descriptive.
Obtinem urmatoarele rezultate.
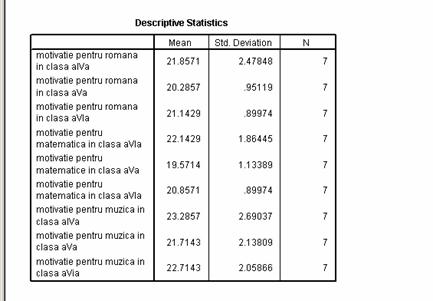
Vom analiza in continuare conditia de sfericitate - corespondentul omogenitatii variantelor de design-uri inter - subiect.

Asa cum stim, putem intalni aici doua situatii:
* cea in care conditia de sfericitate este indeplinita - situatia prezenta la noi pentru variabila disciplina pentru care obtinem un Mauchly's W = .725 care are un prag de semnificatie de .448 > .05 (pragul critic) impreuna cu situatia interactiunii clasa X disciplina pentru care W = .074 si p = .275.
* situatia in care sfericitatea nu este indeplinita - este cazul variabilei clasa pentru care obtinem o valoare a testului Mauchly's W = .301 care are un prag de semnificatie de p = .50 (adica exact valoarea critica). In aceasta situatie va trebui sa analizam aproximarile lui Epsilon si sa reamintim ca daca aproximarile lui Epsilon se situeaza intre .75 si .90 se recomanda utilizarea corectiei Huynh - Feldt, iar daca sunt mai mici se recomanda utilizarea corectiei Greenhous e - Geisser. Analizand in continuare constatam ca aproximarile lui Epsilon in cazul nostru se situeaza sub .75 adica [.598 si .647] conditie in care vom interpreta valorile lui F corespunzatoare corectiei Greenhous e - Geisser.
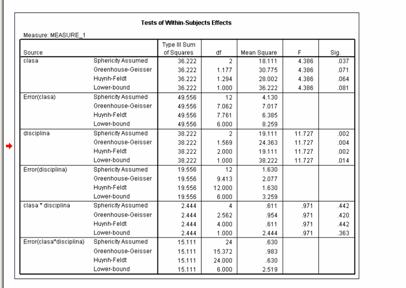
Ca urmare vom putea spune ca pentru variabila clasa unde sfericitatea nu este indeplinita si utilizam corectia Greenhous e - Geisser obtinem un F (1.17, 7.06) = 4.386 si un p = .071 > .05, adica sansele ca aceste diferente sa fie datorate hazardului sau intamplarii sunt de 7% mai mari decat pragul critic de 5% admis de cercetare, in consecinta nu ne putem pronunta cu privire la efectele etapei de dezvoltare in care se situeaza elevii asupra motivatiei lor pentru scoala.
Referindu-ne la interactiunea dintre cele doua variabile analiza statistica evidentiaza un F (4,24) = .971 semnificativ la un prag p = .442 > pragul critic de .05, deci sansele ca aceste diferente sa fie datorate hazardului sau intamplarii sunt de 44%, deci foarte mari vis-a-vis de pragul critic admis in cercetare de 5%. In consecinta studiul intreprins de noi ne pune in evidenta interactiunea celor doua variabile.
In ceea ce priveste disciplina, analiza statistica releva un F(2,12) = 11.727 si un prag de semnificatie p = .02 (aici conditia de sfericitate este indeplinita, deci interpretam prima linie cea cu Sphericity Assumed). In consecinta sansele ca rezultatele sa se datoreze hazardului fiind foarte mici, de 2 % (comparativ cu pragul critic de 5%) putem sustine existenta unor diferente in motivatia subiectilor in functie de disciplina studiata.
Testul F este un test global si in consecinta el ne spune ca undeva intre motivatiile la cele trei discipline analizate exista diferente semnificative fara insa a ne spune unde exact exista aceste diferente. Pentru a evidentia diferentele existente vom folosi testele post - hoc si anume testul post - hoc Bonferroni, considerat ca cea mai buna metoda de a testa diferentele dintre grupe.

![]()
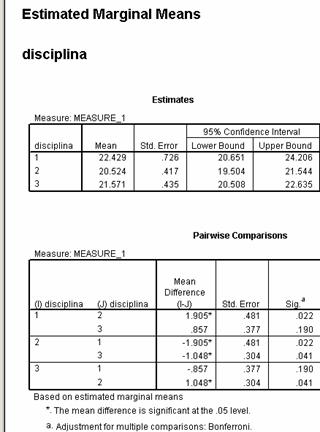
Analizand datele din tabel observam ca exista diferente semnificative intre motivatia elevilor din clasele IV - VI pentru romana si motivatia acelorasi elevi pentru matematica, diferenta mediilor = 1.905 si p =.007 (sig din tabel).
De asemenea diferente semnificative intalnim si intre motivatia elevilor din aceasta etapa de varsta, pentru matematica si motivatia pentru muzica, media diferentelor = 1.048 si p = .014 mai mic decat pragul critic p = .05.
Studiul intreprins nu pune in evidenta diferente semnificative intre motivatia pentru romana si cea pentru muzica p = .063 > p critic = .05.
Putem concluziona ca in aceasta etapa de varsta ( clasele IV - VI) din cele trei discipline analizate (romana, matematica si muzica) matematica este cea pentru care elevii manifesta cea mai scazuta motivatie. Acest lucru se poate evidentia si pe grafic.
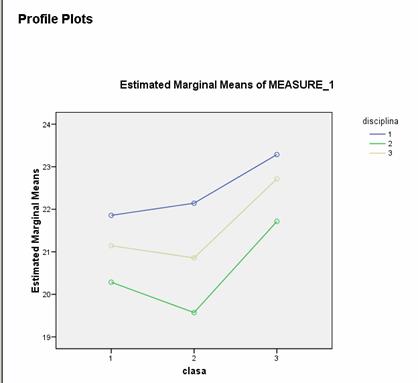
Exemplu 5
Problema
Anova mixt
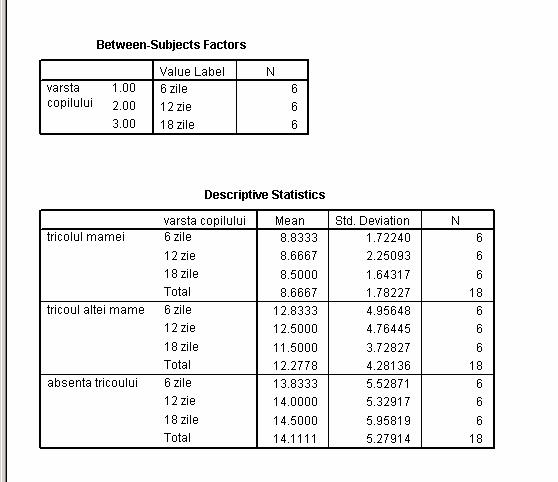
Un psiholog specialist in olfactia sugarilor vrea sa afle daca mirosul mamei, despre care se stie ca este discriminat rapid (intre 6 si 18 zile), poate alina comportamentul bebelusului. In acest scop, masoara timpul in care au adormit dupa supt 6 bebelusi, de 12 zile si de 18 zile. Se efectueaza trei masuratori pentru fiecare bebelus: dupa ce i se pune in patut un tricou purtat de mama, un tricou purtat de mama unui alt copil de aceeasi varsta sau nici un tricou (ordinea fiind aleatorie pentru fiecare bebelus). Timpii de adormire sunt urmatorii ( in minute):
|
|
Tricoul mamei |
Tricoul altei mame |
Tricou absent |
|
6 zile |
6 8 9 9 11 10 |
5 11 12 14 15 20 |
6 10 14 14 17 22 |
|
12 zile |
5 7 9 10 10 11 |
5 10 12 14 15 19 |
6 10 14 16 17 21 |
|
18 zile |
6 7 9 9 10 10 |
5 10 12 12 15 15 |
6 10 14 17 17 23 |
Pasul 1
Identificarea variabilelor
Variabilele independente
A - stimulul olfactiv
a1 - mirosul mamei
a2 - mirosul altei mame
a3 - miros absent
Din punct de vedere al variabilei A avem un design intrasubiect.
B - varsta subiectului
b1 - 6 zile
b2 - 12 zile
b3 - 18 zile
Din punct de vedere al variabilei B avem un design intersubiect.
Variabila dependenta
X - comportamentul bebelusului operationalizat prin timpii de adormire.
Pasul 2
Designul cercetarii
Avem un design bifactorial mixt - inter si intrasubiect 3X3.
|
|
a1 |
a2 |
a3 |
|
b1 |
|
|
|
|
b2 |
|
|
|
|
b3 |
|
|
|
Pasul 3
Ipotezele cercetarii
Vom avea 3 ipoteze, cate una pentru fiecare factor, A si B, si una pentru interactiunea AXB.
Pentru factorul A ipoteza
va fi:
Comportamentul bebelusului este influentat semnificativ de tipul
stimulului olfactiv detectat.
Sau
Exista diferente semnificative in comportamentul bebelusului in functie de tipul stimulului olfactiv detectat.
Pentru factorul B ipoteza va fi:
Comportamentul bebelusului va fi influentat semnificativ de varsta bebelusului.
Sau
Exista diferente semnificative in comportamentul bebelusului in functie de varsta bebelusului.
Pentru interactiunea AXB ipoteza va fi:
Comportamentul bebelusului este influentat semnificativ de interactiunea dintre tipul stimulului si varsta bebelusului.
Sau
Exista diferente semnificative in comportamentul bebelusului in functie de interactiunea dintre tipul stimulului si varsta bebelusului.
Pasul 4
Realizarea bazei de date si alegerea metodei statistice
Intrebarea pe care ne-o punem este "Ce stim despre un subiect?"
Inventariind aflam ca despre fiecare bebelus stim:
1. ce varsta are
2. timpul necesar adormirii in prezenta tricoului propriei mame
3. timpul necesar adormirii in prezenta tricoului altei mame
4. timpul necesar adormirii in absenta tricoului.
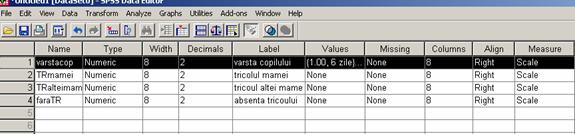
Deci in faza de date vom avea patru coloane, pe fiecare dintre acestea situandu-se una din variabilele mai sus mentionate asa cum se poate vedea in ecranul de mai sus din meniul Variable View.
Sa nu uitam ca in baza de date avem o variabila independenta A pentru care avem un design intersubiect si o variabila B in cadrul careia avem trei masurari ale variabilei dependente (fiind vorba de un design intrasubiect).
Pentru a vedea baza de date propriu-zisa ne uitam in meniul Data View, de mai jos.
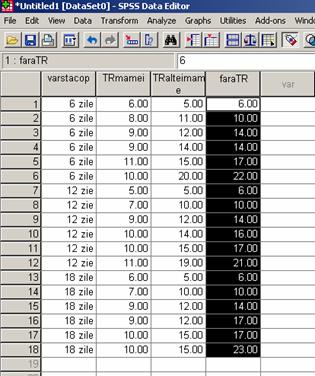
Pentru a decide cu privire la metoda statistica aleasa va trebui sa verificam forma distributiei datelor motiv pentru care vom apela la Split File pentru a imparti subiectii in functie de modalitatile variabilei B pentru care avem un design intersubiect.
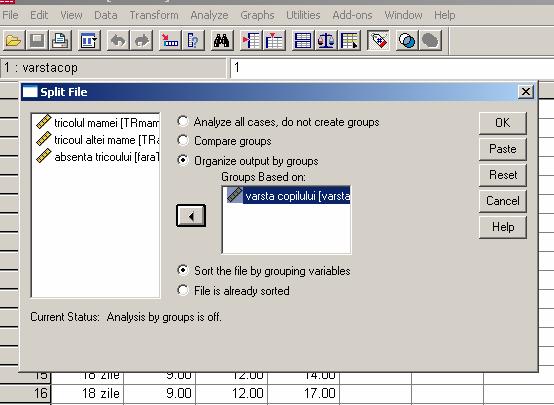
Verificam apoi forma distributiei cu testul Kolmogorov - Smirnov.
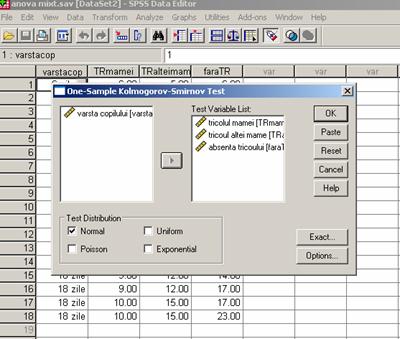
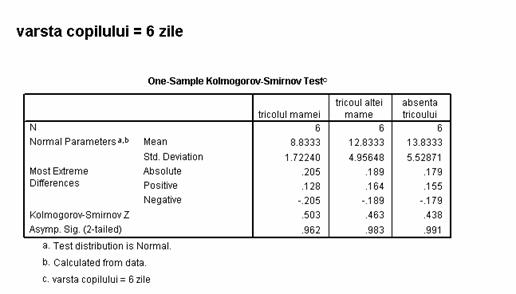


Cum valorile calculate ale testului Kolmogorov - Smirnov ii corespund valori ale pragului de semnificatie situate intre .920 si 1.00 rezulta ca distributiile datelor respecta criteriul de normalitate, in consecinta vom opta pentru o metoda de analiza statistica parametrica.
Tinand cont de tipul de design si de faptul ca distributia datelor respecta criteriul de normalitate vom opta pentru ANOVA mixt al carui corespondent in SPSS este Repeated Measures.

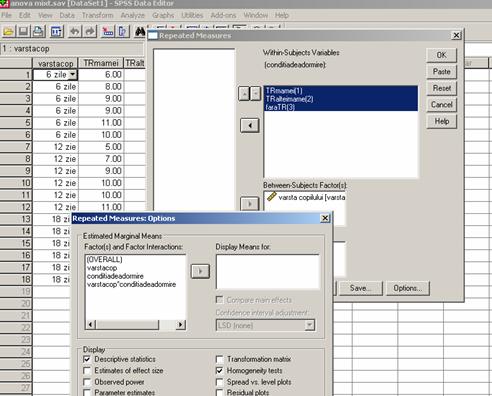
 Modalitatile variabilei A, pentru
care avem design intrasubiect
Modalitatile variabilei A, pentru
care avem design intrasubiect
Variabila B pentru care avem design intersubiect
Dupa introducerea variabilelor in casute, respectiv a masurarilor variabilei independente A pentru care avem design intrasubiect in casuta de mai sus si a variabilei independente B in casuta de mai jos deasupra careia scrie (Between Subjects Factor) vom selecta butonul Options situat in dreapta jos pentru a cere calculul statisticilor descriptive si pentru a verifica sfericitatea datelor in cazul variabilei A pentru care avem un design intrasubiect. (vom bifa Homogenity Test).
Rezultatele sunt redate mai jos.
Analizand rezultatele testului de sfericitate Mauchly's W = .429 semnificativ la un prag p = .003 mai mic decat pragul critic p = .05 deci conditia de sfericitate este incalcata. Vom analiza in continuare cele doua aproximari ale lui Epsilon, acestea situandu-se in intervalul [ .637 si .762] deci mai mici de .75 ceea ce ne indica sa folosim corectia Greenhouse - Geiseer.
Sa interpretam in continuare rezultatele pentru variabila A, pentru care avem un design intrasubiect. Prin urmare obtinem un test F omnibuz F (1.27, 19.09) = 30. 19 la un p = .000 mai mic decat pragul critic p = .05 deci putem spune ca exista diferente semnificative intre reactiile copilului in functie de conditia de adormire, fara a putea preciza prea multe pentru moment. Vom face testele post - hoc Bonferroni pentru a pune in evidenta unde anume exista diferente.
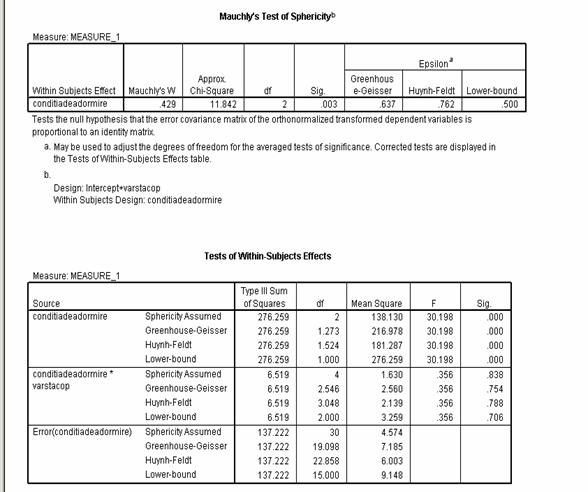
In ceea ce priveste interactiunea dintre variabilele A si B, adica conditia de adormire a copilului si varsta acestuia, obtinem un F ( 2.54, 19.09) = .356 semnificativ la un p = .754, care este mai mare decat pragul critic p = .05 deci sansele ipotezei nule fiind mari studiul nu pune in evidenta interactiunea intre conditia de adormire si varsta copiilor.
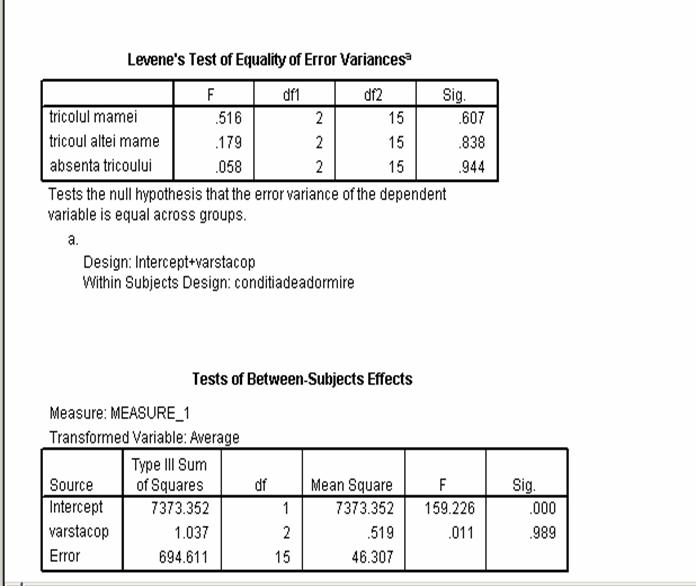
In ceea ce priveste variabila B adica varsta copiilor constatam ca egalitatea variantelor este respectata deoarece pragurile de semnificatie ale testelor Levene's sunt situate intre .607 si .944 adica mai mari decat pragul critic de .05.
Referindu-ne la efectele factorului varsta bebelusului in design obtinem un F (2,15) = .011 la un p = .989 mai mare decat pragul critic p = .05 ceea ce ne permite sa spunem ca sansele ipotezei nule sunt mai mari decat pragul critic p = .05, deci studiul intreprins nu pune in evidenta diferente semnificative in ceea ce priveste timpul de adormire in functie de varsta bebelusilor.
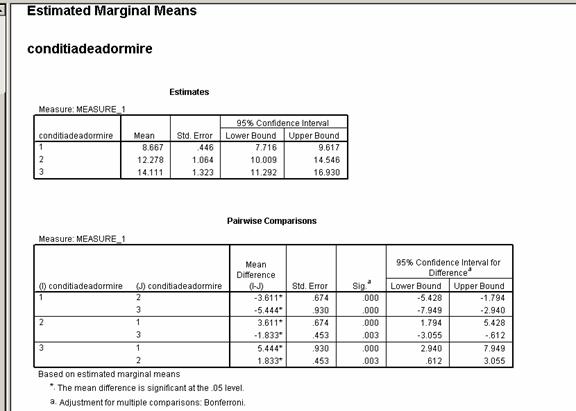
Analizand testele post - hoc Bonferroni pentru conditia de adormire, pune in evidenta existenta unor diferente puternic semnificative intre toate grupurile de conditii analizate, valorile pragului de semnificatie ale mediei diferentelor fiind situate intre .000 si .003 mai mici decat pragul critic p = .05.
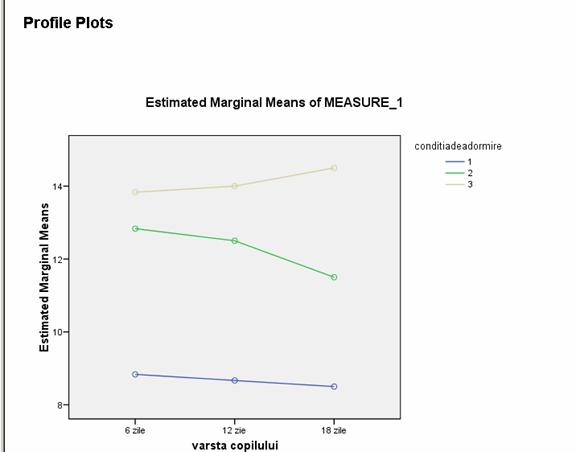
Analizand datele constatam modificari semnificative ale comportamentului bebelusilor in toate cele trei conditii experimentale studiate. Copiii adorm semnificativ mai repede in prezenta stimulului olfactiv matern decat in prezenta unui stimul olfactiv al altei mame sau in lipsa oricarui stimul olfactiv. De asemenea, se constata ca existenta unui stimul olfactiv al altei mame determina o imbunatatire a timpului de adormire comparativ cu situatii absentei unui stimul olfactiv.
Rezultatele sunt evidente si pe graficul mediilor.
Copyright © 2024 - Toate drepturile rezervate