 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
Serii de puteri de variabila complexa
Definitia 1. Se numeste serie de puteri de variabila zIC o serie de forma
![]() , (1)
, (1)
unde
constantele ak![]() C se numesc
coeficientii seriei de puteri.
C se numesc
coeficientii seriei de puteri.
Observatia 1.
Polinoamele sunt serii de puteri pentru orice zIC ( numite functii intregi ) de
un tip particular, unde ![]() iar k este gradul polinomului respectiv.
iar k este gradul polinomului respectiv.
Teorema 1.
(Abel, 1826). Pentru orice serie de puteri,![]() putem asocia un numar real pozitiv R (eventual nul sau infinit) astfel incat:
putem asocia un numar real pozitiv R (eventual nul sau infinit) astfel incat:
i) seria ![]() converge absolut pentru
converge absolut pentru ![]() z, cu
z, cu ![]() ;
;
ii) seria ![]() este divergenta
pentru
este divergenta
pentru ![]() cu
cu ![]() .
.
Numarul R I ] se numeste
raza de convergenta a
seriei date si evident depinde numai de coeficientii ![]() ai seriei.
ai seriei.
Demonstratie.
i). Presupunem ca exista ![]() a.i. seria
a.i. seria ![]() este convergenta (exista
este convergenta (exista ![]() , eventual
, eventual ![]() ). Atunci ( )
). Atunci ( ) ![]() a.i.
a.i. ![]() , deci
, deci
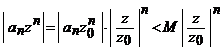 .
.
Urmeaza
ca seria ![]() este convergenta
pentru toate valorile lui z situate
in interiorul cercului
este convergenta
pentru toate valorile lui z situate
in interiorul cercului ![]() , fiind majorata de progresia geometrica cu
ratia subunitara
, fiind majorata de progresia geometrica cu
ratia subunitara ![]() .
.
ii). Daca seria
este divergenta in z0
atunci, pentru orice zIC, cu ![]() , seria este divergenta .
, seria este divergenta .
Daca
seria ![]() converge pentru orice z cu
converge pentru orice z cu ![]() si este
divergenta pentru valorile lui z cu
si este
divergenta pentru valorile lui z cu ![]() , atunci
, atunci ![]() .
.
Observatia 2.
Daca nu exista alte puncte de convergenta decat ![]() atunci,
atunci, ![]() .
.
Calculul razei de convergenta ( Cauchy 1821 si ulterior Hadamard ).
Teorema Cauchy-Hadamard.
Daca exista limita superioara ![]() , atunci raza de
convergenta a seriei are valoarea
, atunci raza de
convergenta a seriei are valoarea ![]() (criteriul
raportului).
(criteriul
raportului).
Daca
exista ![]() , atunci raza de
convergenta R este
egala cu
, atunci raza de
convergenta R este
egala cu ![]() (criteriul
radacinii) si putem scrie
(criteriul
radacinii) si putem scrie
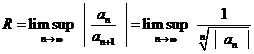 . (2)
. (2)
Se pot considrea serii de puterii de forma
![]() . (3)
. (3)
Folosind
notatia ![]() , rezultatele de mai sus se aplica seriei de puteri
, rezultatele de mai sus se aplica seriei de puteri
![]() ,
,
care este
convergenta in cercul de convergenta ![]() .
.
Fie
![]() si
si ![]() . In
. In ![]() seria de puteri (1)
este absolut convergenta, adica seria
seria de puteri (1)
este absolut convergenta, adica seria
![]() , (
, (![]() )
)
este convergenta.
Evident, pentru orice ![]() care este situat in
discul
care este situat in
discul ![]() ,
,
are loc inegalitatea
![]() .
.
De
aici rezulta ca in discul plin ![]() seria (1) este uniform convergenta pentru ca
termenii ei sunt majorati respectiv, de termenii seriei numerice
seria (1) este uniform convergenta pentru ca
termenii ei sunt majorati respectiv, de termenii seriei numerice ![]() care sunt
independenti de
care sunt
independenti de ![]() .
.
In concluzie, pentru orice ![]() , seria de puteri (1) converge
absolut si uniform in
, seria de puteri (1) converge
absolut si uniform in ![]() si este
divergenta daca
si este
divergenta daca ![]() . Pe circumferinta cercului de convergenta,
deci in punctele
. Pe circumferinta cercului de convergenta,
deci in punctele ![]() pentru care
pentru care ![]() , nu putem afirma nimic care sa ramana valabil
pentru orice serie (1). Pe circumferinta cercului de convergenta
pot exista puncte de convergenta absoluta, de
convergenta sau de divergenta.
, nu putem afirma nimic care sa ramana valabil
pentru orice serie (1). Pe circumferinta cercului de convergenta
pot exista puncte de convergenta absoluta, de
convergenta sau de divergenta.
Definitia 2.
Spunem ca functia ![]() , definita in domeniul
, definita in domeniul ![]() , este
reprezentabila printr-o serie de puteri in D, daca pentru orice z0ID exista un disc
, este
reprezentabila printr-o serie de puteri in D, daca pentru orice z0ID exista un disc ![]() si o serie de
puteri (3) care converge la
si o serie de
puteri (3) care converge la ![]() pentru toti
pentru toti ![]() .
.
Operatii algebrice cu serii de puteri
Fie
seriile de puteri 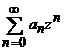 si
si 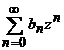 , cu razele de
convergenta respectiv R1
si R2 atunci,
, cu razele de
convergenta respectiv R1
si R2 atunci,
a) seria 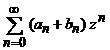 are raza de convergenta
are raza de convergenta ![]() care satisface una din relatiile
care satisface una din relatiile
![]() daca
daca ![]() sau
sau![]() daca
daca ![]() (4)
(4)
si pentru
orice zIC cu ![]() are loc egalitatea
are loc egalitatea
![]() . (5)
. (5)
b) seria produs![]() are raza de convergenta egala cu
are raza de convergenta egala cu ![]() care satisface
conditia
care satisface
conditia ![]() si egalitatea
si egalitatea
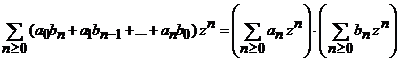 , (6)
, (6)
are loc numai pentru zIC, cu ![]() .
.
Exercitiul
1. Aratati ca daca seriile de puteri ![]() si
si ![]() au respectiv, razele de convergenta R1, R2 si R,
iar
au respectiv, razele de convergenta R1, R2 si R,
iar ![]() atunci
atunci ![]() .
.
![]() Vom
presupune ca seriile de puteri
Vom
presupune ca seriile de puteri ![]() si
si ![]() converg simultan in
converg simultan in ![]() . Atunci, seria de puteri
. Atunci, seria de puteri 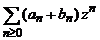 converge in
converge in![]() si deci
si deci ![]() . Aratam ca R nu poate fi strict mai mare decat
. Aratam ca R nu poate fi strict mai mare decat ![]() . In adevar, daca
. In adevar, daca ![]() atunci, putem alege
atunci, putem alege ![]() astfel incat
astfel incat ![]() si deci seria
numerica
si deci seria
numerica ![]() este divergenta
iar seriile
este divergenta
iar seriile ![]() si
si ![]() sunt convergente.
Aceasta concluzie este imposibila deoarece
sunt convergente.
Aceasta concluzie este imposibila deoarece ![]() .
.
Exercitiul
2. Fie seriile de puteri ![]() si
si ![]() cu razele de convergenta
cu razele de convergenta ![]() , respectiv
, respectiv ![]() si fie
si fie ![]() raza de convergenta a seriei suma
raza de convergenta a seriei suma ![]() , iar
, iar ![]() raza de
convergenta a seriei produs
raza de
convergenta a seriei produs![]() .
.
i). Dati exemple
de serii de puteri astfel incat ![]() sa fie superior
lui
sa fie superior
lui ![]() .
.
ii).Dati exemple de
serii de puteri astfel incat ![]() sa fie superior
lui
sa fie superior
lui ![]() .
.
Indicatie. i). Este necesar ca ![]() . Fie
. Fie ![]() si
si ![]() atunci, seriile de
puteri
atunci, seriile de
puteri 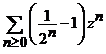 si
si ![]() au razele de
convergenta egale,
au razele de
convergenta egale, ![]() si deci sunt
convergente in multimea
si deci sunt
convergente in multimea ![]() .
.
Seria
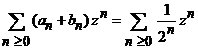 , (7)
, (7)
are raza de
convergenta ![]() .
.
ii). In acest caz vom considera doua exemple:
Exemplul
1. Fie seria ![]() ( cu coeficientii
( cu coeficientii
![]() nuli pentru
nuli pentru ![]() ). Aceasta serie se reduce la un polinom si, in
consecinta, are raza de convergenta
). Aceasta serie se reduce la un polinom si, in
consecinta, are raza de convergenta ![]() .
.
Seria
![]() ( cu coeficientii
( cu coeficientii
![]() , ( )
nIN
, ( )
nIN
are
raza de convergenta ![]() .
.
Deducem ca seria produs,
![]() , unde
, unde 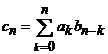 , (8)
, (8)
are coeficientii de forma:
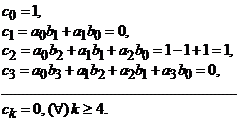 (9)
(9)
Pe de alta parte, avem
![]() , pentru orice zIC,
, pentru orice zIC,
si
![]() , pentru orice zIC, cu
, pentru orice zIC, cu ![]() .
.
De aici deducem ca seria produs are forma
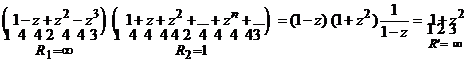 , (10)
, (10)
cu raza de convergenta ![]() , iar egalitatea (10) are loc pentru zIC, cu
, iar egalitatea (10) are loc pentru zIC, cu ![]() .
.
Exemplul 2. Consideram seriile de puteri
![]() , cu raza de convergenta
, cu raza de convergenta ![]() (11)
(11)
si
![]() cu raza de convergenta R2=1. (12)
cu raza de convergenta R2=1. (12)
Atunci, seria produs are forma
![]() , (13)
, (13)
si
are raza de convergenta ![]() .
.
Fie
seria de puteri 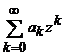 , convergenta pentru
, convergenta pentru ![]() , atunci suma sa defineste, pe multimea de
convergenta, o functie notata
, atunci suma sa defineste, pe multimea de
convergenta, o functie notata ![]() .
.
Daca
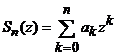 si
si 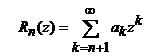 . (14)
. (14)
sunt
respectiv, sirul numerelor partiale si restul de rang n al seriei de puteri, atunci pentru
orice z cu ![]() au loc
egalitatile:
au loc
egalitatile:
![]() . (15)
. (15)
Altfel
spus, seria de puteri ![]() este convergenta pe multimea
este convergenta pe multimea ![]() daca si
numai daca
daca si
numai daca ![]() astfel incat
astfel incat
![]() . (16)
. (16)
Seria
de puteri ![]() este uniform convergenta pentru
este uniform convergenta pentru ![]() daca si
numai daca
daca si
numai daca ![]() astfel incat ( )
astfel incat ( )
![]() cu
cu ![]() sa avem
sa avem
![]() . (17)
. (17)
Teorema 2. Fie ![]() o serie de puteri
si fie R raza sa de convergenta. Atunci
o serie de puteri
si fie R raza sa de convergenta. Atunci
i) Seria de puteri converge uniform in ![]() .
.
ii) Suma seriei de
puteri este o functie ![]() , continua in interiorul cercului de
convergenta
, continua in interiorul cercului de
convergenta ![]() .
.
iii) Daca
raza de convergenta a seriei de puteri este nenula (![]() ) atunci seria de puteri se poate deriva termen cu termen in
) atunci seria de puteri se poate deriva termen cu termen in ![]() si seria
derivatelor are aceeasi raza de convergenta R.
si seria
derivatelor are aceeasi raza de convergenta R.
Observatia 3.
Coeficientii ![]() ai seriei de puteri
ai seriei de puteri
![]() , (18)
, (18)
in
cercul de convergenta ![]() sunt definiti de
formulele
sunt definiti de
formulele
![]() . (19)
. (19)
iar seria
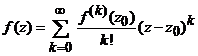 ,
,
se
numeste seria Taylor pentru
functia ![]() .
.
Demonstratie.
i) Fie ![]() si
si ![]() , atunci
, atunci ![]() iar seria
numerica
iar seria
numerica ![]() este convergenta.
Din criteriul lui Weierstrass rezulta ca seria de puteri
este convergenta.
Din criteriul lui Weierstrass rezulta ca seria de puteri ![]() este uniform
convergenta (r poate fi luat
oricat de aproape de R).
este uniform
convergenta (r poate fi luat
oricat de aproape de R).
ii) Fie ![]() unde
unde ![]() este raza de
convergenta a seriei de puteri. Atunci, din uniform convergenta
seriei de puteri, rezulta ca pentru
este raza de
convergenta a seriei de puteri. Atunci, din uniform convergenta
seriei de puteri, rezulta ca pentru ![]() astfel incat
astfel incat ![]()
![]() si
si ![]() cu
cu ![]() .
.
Fie
acum, ![]() fixat astfel incat
fixat astfel incat ![]() si
si ![]() ,
, ![]() si pentru orice
si pentru orice ![]() astfel incat
astfel incat ![]() ,
, ![]() . Atunci pentru
. Atunci pentru ![]() avem
avem
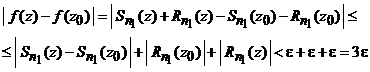
(aici s-a folosit faptul ca ![]() este o suma
finita de functii continue in
este o suma
finita de functii continue in ![]() , deci
, deci ![]() astfel incat
astfel incat ![]() pentru
pentru ![]() ).
).
iii) Notam cu
![]() , atunci functiile
, atunci functiile ![]() sunt continue si
derivabile pentru orice
sunt continue si
derivabile pentru orice ![]() si au derivate
egala cu
si au derivate
egala cu ![]()
Seria
![]() converge in discul
converge in discul ![]() si are suma f(z),
iar seria derivatelor
si are suma f(z),
iar seria derivatelor ![]() , converge absolut in
, converge absolut in ![]() si uniform in
si uniform in ![]() . In adevar, termenul general
. In adevar, termenul general ![]() admite majorarea
admite majorarea
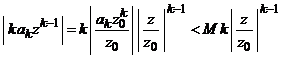
in ![]() si folosind
notatia
si folosind
notatia 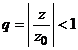 rezulta ca
seria numerica convergenta
rezulta ca
seria numerica convergenta ![]() , majoreaza seria
, majoreaza seria ![]() . Deci aceasta serie este uniform convergenta in
. Deci aceasta serie este uniform convergenta in ![]() catre o
functie
catre o
functie 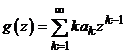 .
.
Afirmatia ca ![]() rezulta din
Observatia 3.
rezulta din
Observatia 3.
Observatia 4.
Daca seria de puteri 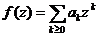 este convergenta
in
este convergenta
in ![]() , atunci seria de puteri
, atunci seria de puteri 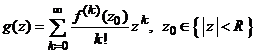 are raza de
convergenta
are raza de
convergenta ![]() unde
unde ![]() , iar
, iar ![]() este derivata de
ordinul k a functiei
este derivata de
ordinul k a functiei ![]() si in plus are
loc egalitatea
si in plus are
loc egalitatea
![]() pentru orice
pentru orice ![]() cu proprietatea
cu proprietatea ![]() .
.
In
adevar, fie ![]() , atunci pentru orice
, atunci pentru orice ![]() avem
avem
![]() si deci, seria
numerica
si deci, seria
numerica 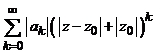 , este convergenta.
, este convergenta.
Pe de alta parte, se poate scrie
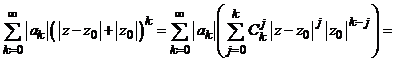
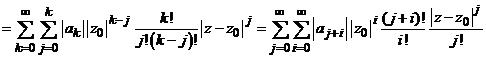
Calculand
derivatele de ordin j ale
functiei ![]() in punctul
in punctul ![]() obtinem
obtinem
![]()
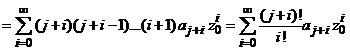
si atunci
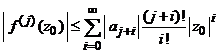
care inlocuita in relatia de mai sus arata ca seria
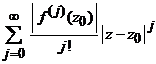 ,
,
este convergenta in cercul ![]() si deci pentru
raza de convergenta
si deci pentru
raza de convergenta ![]() a seriei
a seriei ![]() exista
relatia
exista
relatia ![]() . Daca in plus se alege z astfel incat
. Daca in plus se alege z astfel incat ![]() , avem
, avem
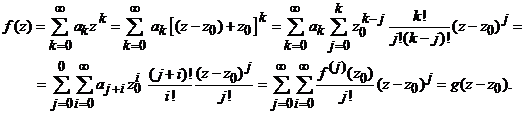
Observatia 5.
Daca 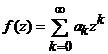 este o serie de puteri
convergenta in
este o serie de puteri
convergenta in ![]() atunci
atunci
![]() .
.
In
adevar, fie ![]() , din observatia 2, avem
, din observatia 2, avem
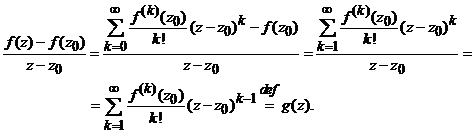
Cum functia g(z) este continua
in cercul cu centrul in z0
si de raza ![]() si
si ![]() , atunci
, atunci
![]()
Observatia 6 Fie seriile
convergente ![]() si
si ![]() avand razele de
convergenta
avand razele de
convergenta ![]() respectiv
respectiv ![]() . Daca exista
. Daca exista ![]() astfel incat pentru
orice z cu
astfel incat pentru
orice z cu ![]() avem
avem ![]() si atunci pentru
si atunci pentru ![]() avem
avem
![]() .
.
In adevar, deoarece ![]() in
in ![]() rezulta ca
rezulta ca ![]() pentru orice
pentru orice ![]() cu
cu ![]() si deci
si deci ![]() de unde obtinem
de unde obtinem ![]() . Din ultima egalitate rezulta
. Din ultima egalitate rezulta ![]() .
.
Exercitiul 1. Sa se arate ca seriile de puteri, definite mai jos, au respectiv razele de convergenta specificate:
![]() .
.
(Functia exponentiala, exp(z), este definita si converge uniform si absolut pe orice submultime marginita a planului).
Din convergenta absoluta a seriei exp(z) deducem ca are loc relatia:
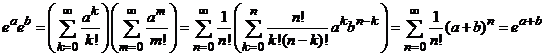 .
.
Aceasta
relatie arata ca pentru orice ![]() avem
avem ![]() .
.
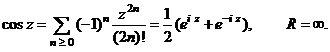
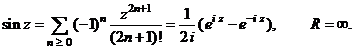
(Seriile
de puteri care definesc functiile trigonometrice ![]() si
si ![]() converg uniform si absolut
pentru orice zIC
converg uniform si absolut
pentru orice zIC
![]() .
.
![]() .
.
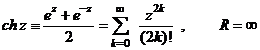 .
.
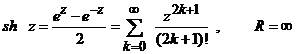 .
.
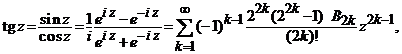
![]() ,
, ![]() .
.
unde
Bn sunt numerele lui Bernoulli:![]() .
.
Indicatie.
Considerand ![]() ca fiind catul
dezvoltarilor functiei
ca fiind catul
dezvoltarilor functiei ![]() prin functia
prin functia ![]() , dezvoltari care exista ( ) si,
intrucat
, dezvoltari care exista ( ) si,
intrucat ![]() este functie
impara, dezvoltarea ei va contine numai puterile impare ale lui z.
este functie
impara, dezvoltarea ei va contine numai puterile impare ale lui z.
Numerele lui Bernoulli satisfac relatia
![]() , (23)
, (23)
care se obtine scriind formal relatiile ![]() si dupa
ridicarea la putere va trebui sa inlocuim puterile
si dupa
ridicarea la putere va trebui sa inlocuim puterile ![]() cu coeficientii
cu coeficientii ![]() . Se poate arata ca toate numerele lui Bernoulli cu
indice impar (afara de
. Se poate arata ca toate numerele lui Bernoulli cu
indice impar (afara de ![]() ) sunt nule.
) sunt nule.
Exercitiul 2. Sa se calculeze razele de convergenta pentru fiecare din seriile de puteri definite mai jos:
i).![]()
Indicatie.
Coeficientii seriei au forma ![]() ,
, ![]() si din teorema
Cauchy-Hadamard deducem ca raza de convergenta este egala
cu
si din teorema
Cauchy-Hadamard deducem ca raza de convergenta este egala
cu ![]() . Deci seria este convergenta
in multimea
. Deci seria este convergenta
in multimea ![]()
ii).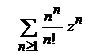
Indicatie.
Coeficientii seriei sunt ![]() ,
, ![]() si raza de convergenta
si raza de convergenta ![]() este
este
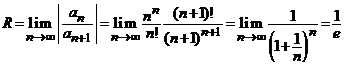 .
.
Deci, seria este convergenta in multimea ![]() .
.
iii). Seria intreaga ![]() are raza de convergenta
are raza de convergenta
![]() .
.
iv).
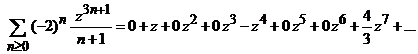
Indicatie. Coeficientii seriei de puteri au forma
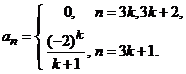
Deoarece
![]() nu are sens pentru
orice
nu are sens pentru
orice ![]() atunci nu putem
utiliza criteriul raportului de la serii de puteri.
atunci nu putem
utiliza criteriul raportului de la serii de puteri.
Fie
sirul 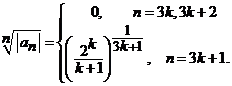 Atunci
Atunci 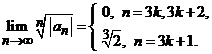
Asadar,
sirul ![]() nu are limita. Cum acest sir are punctele de
acumulare (puncte limita)
nu are limita. Cum acest sir are punctele de
acumulare (puncte limita) ![]() si
si ![]() atunci, acest sir
are limita superioara egala
cu
atunci, acest sir
are limita superioara egala
cu ![]() si din criteriul
radacinii obtinem ca raza de convergenta
si din criteriul
radacinii obtinem ca raza de convergenta ![]() a seriei de puteri date
este
a seriei de puteri date
este ![]() .
.
Altfel. Folosind
rezultatele de la serii numerice, vom nota cu ![]() si obtinem
si obtinem
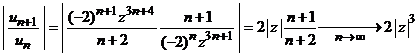 .
.
Daca
![]() atunci
atunci ![]() si rezulta
ca seria
si rezulta
ca seria ![]() este convergenta
deci, seria
este convergenta
deci, seria ![]() este absolute
convergenta.
este absolute
convergenta.
Daca
![]() atunci
atunci ![]() si rezulta
ca seria
si rezulta
ca seria ![]() este divergenta.
este divergenta.
Prin urmare, raza de
convergenta a seriei este egala cu ![]() .
.
v).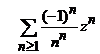 .
.
Indicatie.
Fie 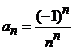 , coeficientii seriei de puteri. Atunci, cu criteriul
radacinii gasim
, coeficientii seriei de puteri. Atunci, cu criteriul
radacinii gasim
![]() ,
,
si deci raza de convergenta a seriei este ![]() .
.
vi). ![]() unde
unde ![]() (constanta).
(constanta).
Indicatie. Coeficientii seriei de puteri au forma
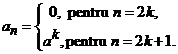
Este
evident ca nu putem calcula ![]() deoarece raportul
deoarece raportul ![]() nu are sens pentru
orice
nu are sens pentru
orice ![]() . Pe de alta parte, avem
. Pe de alta parte, avem 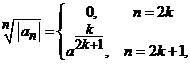 si atunci limita
acestui sir nu exista. Deoarece avem
si atunci limita
acestui sir nu exista. Deoarece avem 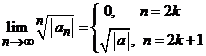 rezulta ca
sirul
rezulta ca
sirul ![]() are
punctele de acumulare
are
punctele de acumulare ![]() si
si ![]() ; deci avem
; deci avem ![]() . Limita superioara a sirului fiind egala cu
. Limita superioara a sirului fiind egala cu ![]() atunci, din criteriul
radacinii lui Cauchy, rezulta ca seria de puteri are raza
de convergenta
atunci, din criteriul
radacinii lui Cauchy, rezulta ca seria de puteri are raza
de convergenta ![]() egala cu
egala cu ![]() .
.
Altfel. Din criteriul
raportului pentru seriile numerice cu termenul general ![]() , cu notatiile
, cu notatiile ![]() obtinem
obtinem 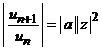 .
.
Deci, daca 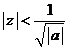 atunci seria
numerica
atunci seria
numerica ![]() .este convergenta si daca
.este convergenta si daca 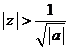 atunci seria
numerica
atunci seria
numerica ![]() este divergenta.
Rezulta ca raza ce convergenta a seriei de puteri este
egala cu
este divergenta.
Rezulta ca raza ce convergenta a seriei de puteri este
egala cu ![]() .
.
Exercitiul 3. Aratati ca:
a). Orice serie de
puteri 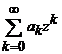 , avand raza de convergenta
, avand raza de convergenta ![]() , converge uniform in cercul
, converge uniform in cercul ![]() .
.
b). Suma seriei de
puteri 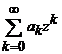 este o functie
continua in interiorul cercului de convergenta.
este o functie
continua in interiorul cercului de convergenta.
c). Seria
obtinuta prin derivarea seriei date, 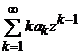 converge absolut in
cercul
converge absolut in
cercul ![]() si uniform in
cercul
si uniform in
cercul ![]() . In adevar,
. In adevar,
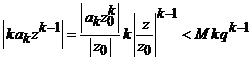 , unde
, unde 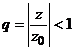
si
cum seria ![]() este convergenta
pentru
este convergenta
pentru ![]() , rezulta ca seria data este convergenta.
, rezulta ca seria data este convergenta.
d).Fie ![]() raza de
convergenta a seriei de puteri
raza de
convergenta a seriei de puteri ![]() ,
,
atunci aceasta serie poate fi derivata termen cu
termen in cercul ![]() si seria
derivata are aceeasi raza de convergenta cu a seriei
date.
si seria
derivata are aceeasi raza de convergenta cu a seriei
date.
Exercitiul 4. Sa se determine raza de convergenta pentru urmatoarele serii intregi:
i).![]() .
.
Indicatie.
Coeficientii seriei intregi au forma ![]()
Rezulta
ca sirul ![]() nu are limita.
nu are limita.
Deoarece
sirul ![]() are doua puncte
de acumulare, 0 si 1, atunci
are doua puncte
de acumulare, 0 si 1, atunci ![]() . Deci seria are raza de convergenta
. Deci seria are raza de convergenta ![]() egala cu
egala cu ![]() .
.
Altfel.
Pentru ca ![]() ia valorile
ia valorile ![]() sau
sau![]() rezulta
rezulta ![]() . Prin urmare, pentru
. Prin urmare, pentru ![]() , seria
, seria ![]() este convergenta
si atunci seria
este convergenta
si atunci seria ![]() este convergenta.
Pentru
este convergenta.
Pentru ![]() , termenul
, termenul ![]() nu converge la zero,
pentru
nu converge la zero,
pentru ![]() si deci, seria
si deci, seria ![]() este divergenta.
Deducem ca raza de convergenta
este divergenta.
Deducem ca raza de convergenta ![]() a seriei de puteri este
egala cu
a seriei de puteri este
egala cu ![]() .
.
ii). 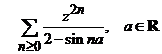 , constanta.
, constanta.
Indicatie.
Fie 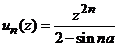 , termenul general al seriei. Atunci
, termenul general al seriei. Atunci
![]()
si
deci seria ![]() converge pentru orice
converge pentru orice ![]() cu
cu ![]() . Asadar, seria
. Asadar, seria ![]() , fiind majorata de seria convergenta cu cu
termenul general
, fiind majorata de seria convergenta cu cu
termenul general ![]() , converge pentru
, converge pentru ![]() si deci, seria
data este absolut convergenta in
si deci, seria
data este absolut convergenta in ![]() Prin urmare putem
scrie ca raza de convergenta verifica inegalitatea
Prin urmare putem
scrie ca raza de convergenta verifica inegalitatea ![]() .
.
Fie acum ![]() , astfel ca
, astfel ca ![]() . Deoarece
. Deoarece ![]() , rezulta ca
, rezulta ca ![]() si deci seria
si deci seria ![]() este divergenta.
In concluzie, seria de puteri are raza de convergenta
este divergenta.
In concluzie, seria de puteri are raza de convergenta ![]() , egala cu
, egala cu ![]() .
.
iii). ![]() .
.
Indicatie.
Din inegalitatile ![]() , rezulta ca seria
, rezulta ca seria ![]() converge absolut
pentru
converge absolut
pentru ![]() si este
divergenta pentru
si este
divergenta pentru ![]() .
.
Exercitiul 5.
Sa se determine raza de convergenta ![]() , a seriei
, a seriei
i).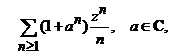 constanta.
constanta.
Indicatie.
Pentru determinarea lui ![]() , cercetam raza de convergenta a seriei
derivate
, cercetam raza de convergenta a seriei
derivate
![]() ,
,
are
este aceeasi cu a seriei ![]() obtinuta evident, prin inmultirea cu
obtinuta evident, prin inmultirea cu ![]() a seriei derivate.
a seriei derivate.
In
continuare vom privi seria ![]() ca suma
a seriilor
ca suma
a seriilor ![]() si
si ![]() , care au respectiv razele de convergenta
, care au respectiv razele de convergenta ![]() si
si ![]() , egale cu
, egale cu ![]() .
.
Daca
![]() atunci
atunci ![]() si obtinem
ca raza de convergenta a sumei celor doua serii este
egala cu numarul
si obtinem
ca raza de convergenta a sumei celor doua serii este
egala cu numarul
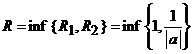 .
.
Daca
![]() atunci
atunci ![]() si deci
si deci ![]() . In acest caz, pentru a preciza valoarile lui
. In acest caz, pentru a preciza valoarile lui ![]() , fie
, fie ![]() , unde
, unde ![]() Atunci
Atunci ![]() si daca vom
presupune
si daca vom
presupune ![]() atunci
atunci ![]() astfel incat
astfel incat ![]() si seria
si seria ![]() sa fie
convergenta. Fie
sa fie
convergenta. Fie ![]() , atunci pentru
termenul general al acestei serii convergente obtinem evaluarea
, atunci pentru
termenul general al acestei serii convergente obtinem evaluarea
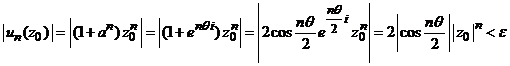 ,
,
pentru
orice ![]() , cu
, cu ![]() ales oarecare. Ultima
inegalitate arata ca
ales oarecare. Ultima
inegalitate arata ca
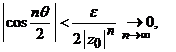 (evident, pentru
(evident, pentru ![]() ).
).
Ori aceasta concluzie este
falsa, de exemplu pentru alegerea ![]() (cand
(cand ![]() ). Deci, rezulta ca daca
). Deci, rezulta ca daca ![]() si
si ![]() atunci raza de
convergenta a seriei este egala cu
atunci raza de
convergenta a seriei este egala cu ![]() .
.
Exercitiul 6. Se considera ecuatia diferentiala
![]() .
.
i). Sa se arate
ca exista o solutie ![]() a ecuatiei date,
care verifica conditia
a ecuatiei date,
care verifica conditia ![]() si care se poate
scrie sub forma seriei de puteri
si care se poate
scrie sub forma seriei de puteri
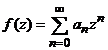 .
.
ii).Exprimati
functia ![]() cu ajutorul
functiilor elementare.
cu ajutorul
functiilor elementare.
Indicatie.
i).Presupunem ca 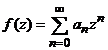 este o solutie a
ecuatiei diferentiale. Atunci seria considerata are o raza
de convergenta
este o solutie a
ecuatiei diferentiale. Atunci seria considerata are o raza
de convergenta ![]() si pe
multimea
si pe
multimea ![]() sunt justificate
operatiile algebrice cu serii de puteri cat si derivarea lor termen
cu termen.
sunt justificate
operatiile algebrice cu serii de puteri cat si derivarea lor termen
cu termen.
Deci 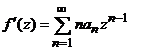 si
si 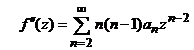 si ecuatia
data devine
si ecuatia
data devine
![]() .
.
Dupa efectuarea inlocuirilor necesare, ultima ecuatie poate fi scrisa dezvoltat sub forma
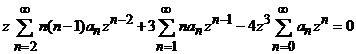
sau
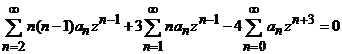
Pentru
a organiza calculul, in ultima suma vom nota ![]() si atunci
si atunci ![]() ; pentru
; pentru ![]() rezulta
rezulta ![]() , apoi facem inlocuirile respective si in final,
dupa renuntarea la virgule, obtinem
, apoi facem inlocuirile respective si in final,
dupa renuntarea la virgule, obtinem
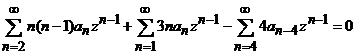
sau, echivalent
![]() .
.
Prin identificarea cu zero se obtin urmatoarele relatii:
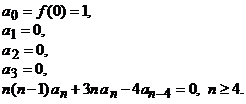
sau
![]()
Asadar, putem scrie
![]() si
si ![]() .
.
Ultima
egalitate arata ca toti coeficientii ![]() sunt nenuli si
pot fi exprimati in functie de
sunt nenuli si
pot fi exprimati in functie de ![]() si
si ![]() sub urmatoarea
forma
sub urmatoarea
forma
![]() .
.
Deci,
este necesar ca functia ![]() sa aiba
forma
sa aiba
forma
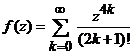 .
.
Seria
de puteri fiind convergenta (avand raza de convergenta
egala cu ![]() ) putem justifica existenta unei solutii
functie intreaga.
) putem justifica existenta unei solutii
functie intreaga.
ii). Din scrierea
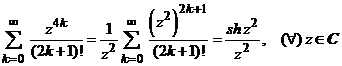 ,
,
rezulta
ca solutia are forma 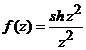 .
.
Copyright © 2025 - Toate drepturile rezervate