Probleme suplimentare : siruri de numere si matrice

Probleme suplimentare : siruri de numere

Fiind dat un vector v cu n elemente numere intregi , sa se afiseze de cate ori gasim doua elemente consecutive egale intre ele.

Sa se afiseze elementele prime ale unui sir de n numere intregi citite de la tastatura .

a) fiind dat un polinom P(x) si un intreg b , sa se calculeze P(b) ; (valoarea lui P pentru o valoare b a argumentului) ;

b) fiind date doua polinoame P(x) si Q(x) , ambele de gradul n , sa se determine suma celor doua polinoame , P(x)+Q(x) , tiparindu-se coeficientii polinomului suma .

Se da un vector v cu n elemente numere intregi . Fara a folosi un vector auxiliar , sa se mute la sfirsitul lui v elementele sale nule , pastrind ordinea celorlalte elemente . exemplu: daca initial v = ( 2 , 3 , 0 , 9 , 0 , 0 , 8 ) , in final va rezulta v

Indicatii. Parcurgem vectorul dat v si pentru fiecare element v[i] testam daca este ; in caz afirmativ , mutam toate componentele din dreapta lui v[i] cu o pozitie mai la stinga , micsoram dimensiunea lui v cu o unitate si incrementam un contor nr care numara elementele nule . In final adaugam nr elemente cu valoarea la sfirsitul lui v

Se da un sir cu n componente naturale ( 1< n < 100 ) . Sa se afiseze cel mai mic numar natural care se poate alcatui luind prima cifra a fiecarui element al sirului . exemplu : pentru n = 4 si elementele ( 234 , 7650 , 19 , 2 ) numarul este 1227 .

Indicatii . Se parcurge sirul memorat intr-un vector v , si pentru fiecare element v[i] retinem prima cifra , pe care o extragem cu algoritmul clasic de impartiri la 10 si o adaugam la sfirsitul unui "vector de cifre" c , initial gol . Sortam crescator vectorul , dupa care prin parcurgerea vectorului sortat de la stinga la dreapta obtinem numarul cerut .

Se citeste de la tastatura un sir cu n elemente numaere naturale , nu neaparat distincte . Sa se afiseze elementul care apare de cele mai multe ori in sir . Daca exista mai multe astfel de elmente , se vor afisa toate . exemplu : pentru n = 5 si elmentele ( 23 , 7 , 11 , 7 ,19 , 7 , 11 , 11 ) se vor afisa elementele si 11 care apar fiecare de trei ori .

Indicatii . Se ordoneaza crescator vectorul v in care memoram sirul . Dupa ordonare , elementele indicate vor fi succesive in vector . Folosim alti doi vectori u si f : fiecare u[i] va fi un element distinct al vectorului v , iar f[i] va reprezenta frecventa de aparitie a lui u[i] in vectorul v . Parcurgem vectorul sortat v si la fiecare pas comparam elementul curent v[i] cu cel urmator v[i+1] ; daca sunt diferite , am identificat un nou element distinct al lui v , "in persoana" lui v[i+1], pe care il adugam la sfirsitul lui u , initializind totodata cu 1 un element nou la sfirsitul vectorului f ; in caz contrar , incrementam componenta din f care indica frecventa elmentelor egale v[i] si v[i+1]

Se citesc de la tastatura doua numere naturale foarte mari , care pot avea pina la 70 de cifre fiecare . Sa se afiseze suma celor doua numere .

Indicatii . Evident ca numere atit de mari nu pot fi reprezentate in memorie nici macar cu ajutorul tipului longint . Singura solutie este sa memoram cifrele lor in vectori . Pentru adunarea celor doua numere vom opera asupra vectorilor . Se parcurg "in paralel" cei doi vectori de cifre de la dreapta la stinga . La fiecare pas , insumeaza elemntele aflate pe pozitii identice in cei doi vectori , cu memorarea rezultatului pe aceeasi pozitie intr-un al treilea vector . Daca o astfel de soma depaseste , inseamna ca elementul corespunzator din vectorul-suma va fi diferenta dintre suma obtinuta si , iar pe de alta parte vom avea un transport egal cu catre pozitia urmatoare . Daca suma nu depaseste , atunci ea se va memora ca atare in vectorul suma .

Se citeste un sir cu n elemente numere naturale . Sa se re-aranjeze numerele in sir , astfel incit cele pare sa ocupe primele pozitii in ordine crescatoare . exemplu : daca sirul initial este(7, 8, 5, 2, 10, 4), atunci dupa re-aranjare devine (2, 4, 8, 10, 7, 5).

Indicatii: Mentionam sirul intr-un vector . Proiectam un ciclu de interschimbari de elemente . La fiecare pas privim vectorul ca fiind alcatuit din doua parti : o parte deja aranjata  ( v[1] , . , v[k-1] ) si o parte ne-aranjata ( v[k] , . , v[n] ) si incercam sa marim partea aranjata cu inca un element . Pentru aceasta , determinam cel mai mic dintre elementele v[k] , . , v[n] ale partii nearanjate si il aducem pe pozitia k prin interschimbare cu v[k] . Initial partea aranjata este vida , iar in final ea va contine tot vectorul , deci pozitia k ce indica "bariera" intre cele doua parti evolueaza de la la n

Indicatii . Retinem in doua variabile p si q pozitiile ce reprezinta capetele fiecarui platou identificat si lungimea maxima in variabila 1max initializata cu . Identificam platourile prin parcurgerea vectorului intr-un ciclu cit timp i <= n . La fiecare pas cautam un platou incepind cu pozitia i , avansind in vector cit timp intilnim elemente consecutive egale ( unde initial i = 1 ) , daca lungimea platoului astfel determinat , adica q-p-1 , este mai mare decit lung_max , atunci ea devine noua lungime maxima . In final printr-o noua parcurgere a vectorului , identificam toate platourile de lungime maxima si le afisam : pentru fiecare element v[i] , testam daca este egal cu v[i+lung_max]

Se citeste de la tastatura un sir de numere naturale . Sa se afiseze toate grupurile de numere din sir care au aceeasi divizori factori primi . exemplu :fie sirul 12 , 15 , 2 , 36 , 32 . Grupurile afisate vor fi : ( 12 , 36 ) cu divizorii primi 2 si 3 , ( 15 ) cu divizorii primi 3 si 5 , ( 2 , 32 ) cu divizorul prim 2 .

Indicatii . Daca sirul are n numere , vom creea doi vectori v si f , astfel : fiecare element v[i] va fi un numar din sirul dat , iar f[i] va reprezenta produsul factorilor primi ai lui v[i] , cu i = 1 , 2 , . , n . Evident ca daca doua elemente ale sirului cu acelasi produs de factori primi , atunci elementele in cauza vor avea aceeasi factori primi , deci in vectorul f se pot evidentia grupurile cerute . Ordonam crescator vectorul f folosind oricare dintre algoritmii de sortare studiati . In final se afiseaza grupurile cerute prin parcurgerea vectorului f , grupurile cerute nefiind altceva decit platourile din vector ( vezi problema anterioara ).
2. Probleme suplimentare: matrice

O matrice patratica a se numeste simetrica fata de diagonala principala , daca fiecare element

de deasupra diagonalei principale este egal cu simetricul sau de sub diagonala , adica a[i, j] =

a[j, i ] pentru orice i j . Scrieti un program care verifica daca o matrice patratica a cu n linii

si n coloane citita de la tastatura , este simetrica fata de diagonala principala.

Se citeste de la tastatura o matrice a cu m linii * n coloane si elemente numere intregi. Sa se

verifice daca doua linii date L1 si L2 sunt identice (contin aceleeasi elemente in aceeasi

dispunere pe coloane) , afisindu-se un mesaj corespunzator.

Sa se afiseze maximul dintre elementele pare ale liniei L a unei matrici cu m linii si n coloane.

Valorile lui n si L , precum si elementele matricii (numere intregi) , se citesc de la tastatura .

Se citeste de la tastatura o matrice a cu m linii * n coloane si elemente numere intregi . Sa se

memoreze intr-un vector b sumele elementelor de pe fiecare linie a matricii ( b[i] va

reprezenta suma elementelor de pe linia i in matrice) .

Se citeste de la tastatura o matrice a cu m linii * n coloane si elemente numere intregi . Sa se

copieze intr-un vector elementele pozitive aflate deasupra diagonalei principale in matrice ,

apoi sa se tipareasca vectorul .

Pentru o matrice data a cu m linii * n coloane si elemente numere intregi , sa se interschimbe

intre ele doua linii date L1 si L2 , fara a folosi alta matrice.

Se citeste de la tastatura o matrice a cu m linii * n coloane si elemente numere intregi . Sa se

determine linia (liniile) din matrice care contin cele mai multe elemente nenule .

Pentru o matrice data a cu m linii * n coloane si elemente numere intregi , sa se elimine o

coloana data C , fara a folosi alta matrice .

Se da o matrice patratica a cu m linii * n coloane si un vector v cu n componente . Ambele

tablouri sunt alcatuite din numere intregi . Scrieti un program care verifica daca vectorul v

apare ca linie in matricea a

Fiind data o matrice a cu m linii * n coloane si elemente numere intregi , sa se construiasca

transpusa acesteia (matricea care se obtine scriind liniile pe coloane si invers) . Exemplu :

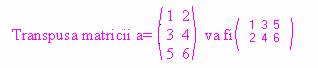
Se citeste de la tastatura o matrice a cu m linii * n coloane si elemente numere intregi . realizati interschimbarile de linii / coloane necesare , astfel incit elementele de pe diagonala principala , citite de sus in jos , sa fie sortate crescator .

Indicatii . Aplicam ideea algoritmului de sortare pentru elementele a[1,1] , . , a[n,n] de pe diagonala principala . Fiecare dintre acestea vor juca pe rind rolul unui pivot ; pentru fiecare pivot a[i,i] , parcurgem intr-un alt ciclu cu j = i+1 , . , n elmente a[j,j] de pe diagonala principala aflate sub pivot . La fiecare pas , daca a[j,j] < a[i,i] atunci trebuie interschimbate cele doua elemente intre ele , dar vom interschimba cu totul liniile si coloanele pe care se afla : mai intii linia i, cu linia j , apoi coloana i cu coloana j

Se da un tablou bidimensional cu m linii si n coloane ( m ,n I , avind ca elemente numai cifre de si . Doua linii se numesc complementare , daca , pentru orice coloana , suma elementelor aflate pe aceeasi coloana este 1 . Sa se identifice perechile de linii complementare si sa se determine numarul acestora . Pentru fiecare astfel de pereche se vor afisa pe un rind al ecranului indicii liniilor ce o compun , separate prin spatii , iar pe ultimul rind se va tiparii numarul perechilor de linii complementare din tablou .

Indicatii . Identificam liniile matricii prin indicii lor . Astfel perechiile de linii vor fi date de perechile de indici de forma ( i1 , i2 ) , cu i1 = 1 , 2 , . , m-1 si i2 = i+1 , . , m . Formam aceste perechi in doua cicluri , si pe fiecare pereche ( i1 , i2 ) testam prin parcurgerea coloanelor "in paralel" daca liniile ce alcatuiesc perechea sunt complementare ( a[i1,j]+a[i2,j]   = 1 pentru orice j = 1 , 2 , . , n ) .

Se citeste de la tastatura un numar natural n ( 1 < n < 6 ) . Sa se construiasca un tablou patratic cu n linii * n coloane avind ca elemente primii n * n termeni ai sirului lui Fibonacci . Ordinea de construire a matricii va fi : a[1,1], . ,a[1,n],a[2,1], . ,a[2,n], . ,a[n,1], . ,a[n,n]

Indicatii . Se copleteaza separat prima linie a matricii , pentru a putea memora primii doi termeni egali cu in elementele a[1,1] si a[1,2] . Celelalte elemente de pe prima linie se completeaza intr-un ciclu in care parcurgem coloanele j de la la n si la fiecare pas , memoram un termen al sirului in elementul a[1,j] . Apoi , completam analog restul matricii in doua cicluri cu i de la la n ( liniile ) si j de la la n ( coloanele ) .

Se citeste o matrice patratica a cu n linii * n coloane si elemente numere intregi sa se afiseze sirul obtinut prin parcurgerea matricii in spirala , pornind din coltul din stinga sus si deplasindu-ne circular pina in centrul matricii .

Exemplu : pentru matricea

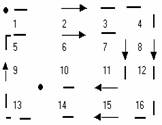
se va afisa sirul 1 2 3 4 8 12 16 15 14 13 9 5 7 11 10 .

Indicatii . Din desen se poate observa ca se formeaza niste "inele" concentrice care trebuie parcurse pe rind . Pentru parcurgerea fiecarui inel avem nevoie de patru cicluri for care sa strabata cele patru laturi ale inelului : sus , dreapta , jos, stinga . Odata stabilita modalitatea de parcurgere a unui inel , trebuie sa generalizam formula pentru toate cele (n+1) div 2 inele .

Se citeste de la tastatura o matrice a cu m linii * n coloane . Sa se elimine atitea linii cite sunt necesare , asa incit elementele coloanei C parcurse de sus in jos sa fie in ordine crescatoare (unde C este cunoscut) .

Indicatii . Se parcurg intr-un ciclu liniile i ale coloanei C , cu i de la la m . Pentru fiecare element a[i,C] , daca este mai mic decit elementul a[i-1,C] aflat pe aceeasi coloana si in linia anterioara , inseamna ca a[i,C] "strica" ordinea crescatoare a coloanei C . In aceasta situatie , trebuie eliminata integral lina i pe care se afla acest element folosind algoritmul dat in capitolul de fata .